Compilers

Start Lecture #12 (Prof. Schonberg)

6.6.3: Flow-of-Control Statements

The lab3 grammar has the following productions concerning flow of control statements.

    program           → procedure-def program | ε
    procedure-def     → PROCEDURE name-and-params IS decls BEGIN statement statements END ;
    statements        → statement statements | ε
    statement         → keyword-statement | identifier-statement
    keyword-statement → return-statement | while-statement | if-statement
    if-statement      → IF boolean-expression THEN statements optional-else END ;
    optional-else     → ELSE statements | ε
    while-statement   → WHILE boolean-expression DO statements END ;
  

I don't show the productions for name-and-parameters, declarations, identifier-statement, and return-statement since they do not have conditional control flow (return just generates a goto, but doesn't use any of the techniques in this section). The production for boolean-expression will be done in the next section.

I don't know why the sections aren't in the reverse order and I came close to reversing the order of presentation.

In this section we will produce an SDD for the productions above under the assumption that the SDD for Boolean expressions generates jumps to the labels be.true and be.false (depending of course on whether the Boolean expression be is true or false).

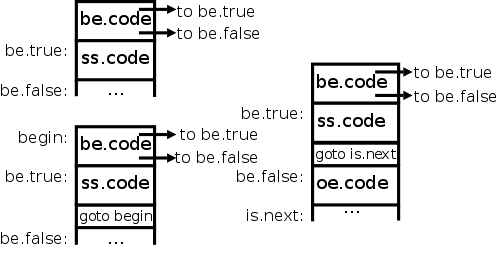
The diagrams on the right give the idea for the three basic control flow statements, if-then (upper left), if-then-else (right), and while-do (lower-left).

If and While SDDs

Production	Semantic Rules
pg → pd pg1	pd.next = newLabel() pg.code = pd.code || label(pd.next) || pg1.code
pg → ε	pg.code = ""
pd → PROC np IS ds BEG s ss END ;	s.next = newLabel() ss.next = pd.next pd.code = s.code || label(s.next) || ss.code
ss → s ss1	s.next = newLabel() ss1.next = ss.next ss.code = s.code || label(s.next) || ss1.code
ss → ε	ss.code = ""
s → ks	ks.next = s.next s.code = ks.code
ks → is	is.next = ks.next ks.code = is.code
is → IF be THEN ss oe END ;	be.true = newLabel() be.false = newLabel() ss.next = is.next oe.next = is.next is.code = be.code || label(be.true) || ss.code ||     gen(goto is.next) || label(be.false) || oe.code
oe → ELSE ss	ss.next = oe.next oe.code = ss.code
oe → ε	oe.code = ""
ks → ws	ws.next = ks.next ks.code = ws.code
ws → WHILE be DO ss END ;	ws.begin = newLabel() be.true = newLabel() be.false = ws.next ss.next = ws.begin ws.code = label(ws.begin) || be.code ||       label(be.true) || ss.code || gen(goto begin)

The table to the right gives the details via an SDD. To enable the tables to fit we abbreviate the names of the non-terminals appearing in the grammar above to pg, pd, np, ds, ss, s, ks, is, rs, ws, is, be, and oe.

The treatment of the various *.next attributes deserves some comment. Each statement (e.g., if-stmt abbreviated is or while-stmt abbreviated ws) is given, as an inherited attribute, a new label *.next. You can see the new label generated in the
stmts → stmt stmts
production and then notice how it is passed down the tree from stmts to stmt to keyword-stmt to if-stmt. The child generates a goto that label if it wants to end (look at is.code in the if-stmt production).

The parent, in addition to sending this attribute to the child, normally places label(*.next) after the code for the child. See ss.code in the
stmts → stmt stmts
production.

An alternative design would have been for the child to itself generate the label and place it as the last component of its code (or elsewhere if needed). I believe that alternative would have resulted in a clearer SDD with fewer inherited attributes. The method actually chosen does, however, have one and possibly two advantages.

1. Perhaps there is a case where it is awkward for the child to place something at the end of its code (but I don't quite see how this could be). To investigate if this second possibility occurs one might want to examine the treatment of case statements below.
   
   
2. Look at ws.code the code attribute for the while statement. The parent (the while-stmt) does not place the ss.next label after ss.code. If we used the alternative where the child (the stmts) generated the ss.next at the end of its code, the parent would need a goto from after ss.code to the begin label. If the child needed to jump to its end it would jump to the ss.next label and the next statement would be the jump to begin. With the scheme we are using we do not have this embarrassing jump to jump sequence.
   
   I must say, however, that, given all the non-optimal code we are generating, it might have been pedagogically better to use the alternative scheme and live with the jump to a jump embarrassment. I decided in the end to follow the book, but am not sure that was the right decision.

Homework: Give the SDD for a repeat statement
    REPEAT ss WHILE be END ;

6.6.4: Control-Flow Translation of Boolean Expressions

Do on the board the translation of

    if ( x < 5 || x > 10 && x == y ) x = 3 ;
  

We get

        if x < 5 goto L2
        goto L3
    L3: if x > 10 goto L4
	goto L1
    L4: if x == y goto L2
	goto L1
    L2: x = 3
    L1:
  

Note that there are three extra gotos. One is a goto the next statement. Two others could be eliminated by using ifFalse.

6.6.5: Avoiding Redundant Gotos

Skipped.

6.6.6: Boolean Values and Jumping Code

If there are boolean variables (or variables into which a boolean value can be placed), we can have boolean assignment statements. That is we might evaluate boolean expressions outside of control flow statements.

Recall that the code we generated for boolean expressions (inside control flow statements) used inherited attributes to push down the tree the exit labels B.true and B.false. How are we to deal with Boolean assignment statements?

Two Methods for Booleans: Method 1

Up to now we have used the so called jumping code method for Boolean quantities. We evaluated Boolean expressions (in the context of control flow statements) by using inherited attributes to push down the tree the true and false exits (i.e., the target locations to jump to if the expression evaluates to true and false).

With this method if we have a Boolean assignment statement, we just let the true and false exits lead respectively to statements

    LHS = true
    LHS = false
  

Two Methods for Booleans: Method 2

In the second method we simply treat boolean expressions as expressions. That is, we just mimic the actions we did for integer/real evaluations. Thus Boolean assignment statements like
a = b OR (c AND d AND (x < y))
just work.

For control flow statements like

    while boolean-expression do statement-list end ;
    if boolean-expression then statement-list else statement-list end ;
  

However, as mentioned before, this is wrong.
In C and other languages if (a=0 || 1/a > f(a)) is guaranteed not to divide by zero and the above implementation fails to provide this guarantee. We must implement short-circuit boolean evaluation.

6.7: Backpatching

Skipped.

Our intermediate code uses symbolic labels. At some point these must be translated into addresses of instructions. If we use quads all instructions are the same length so the address is just the number of the instruction. Sometimes we generate the jump before we generate the target so we can't put in the instruction number on the fly. Indeed, that is why we used symbolic labels. The easiest method of fixing this up is to make an extra pass (or two) over the quads to determine the correct instruction number and use that to replace the symbolic label. This is extra work; a more efficient technique, which is independent of compilation, is called backpatching.

6.8: Switch Statements

      if
      else if
      else if
      ...
      end if
    

6.8.1: Translation of Switch-Statements

6.8.2: Syntax-Directed Translation of Switch-Statements

6.9 Intermediate Code for Procedures

Much of the work for procedures involves storage issues and the run time environment; this is discussed in the next chapter.

In order to support inter-procedural type checking using just one pass over the SDD we need to define the called procedure for use by the calling procedure. The lab3 grammar is not quite capable of this for the general case.

When a procedure (or function) definition is parsed, we could place in the outermost identifier table the signature of the procedure (defined below).

Then when the call is reached the types can be checked. So all is well if the callee precedes the caller, which would be a requirement with the lab3 grammar (this is not strictly true, one could gather up the program while going through the tree and then at the root make a function call—a synthesized attribute—to a procedure that just happens to be another compiler that can handle this case). The requirement that callee precedes caller eliminates the important case of mutual recursion where f calls g and g calls f.

We will not produce SDDs for the special case that can be handled by our grammar.

The basic scheme for type checking procedures is to generate a table entry for the procedure that contains its signature, i.e., the types of its parameters and its result type.

Recall the SDD for declarations. These semantic rules pass up the totalSize to the
      ds → d ds
production.

What is needed is for the ps (parameters) to do an analogous thing with their declarations but also (or perhaps instead) pass up a representation of the declarations themselves which when it reaches the top is the signature for a procedure and when put together with the return is the signature for a function.

More serious is supporting nested procedure definitions (defining a procedure inside a procedure). Lab 3 doesn't support this because a procedure or function definition is not a declaration. It would be easy to enhance the grammar to fix this, but the serious work is that then you need nested identifier tables.

Since our lexer doesn't support this, the parser must produce the nested tables (using the tables that the lexer does generate). When a new scope (procedure definition, record definition, begin block) arises you push the current tables on a stack and begin a new one. When the nested scope ends, you pop the tables.