Compilers

Start Lecture #11

Remark: Lab 4 assigned.

6.4.2: Incremental Translation

We saw this in chapter 2.

The method in the previous section generates long strings as we walk the tree. By using SDT instead of using SDD, you can output parts of the string as each node is processed.

6.4.3: Addressing Array Elements

The idea is that you associate the base address with the array name. That is, the offset stored in the identifier table entry for the array is the address of the first element. When an element is referenced, the indices and the array bounds are used to compute the amount, often called the offset (unfortunately, we have already used that term), by which the address of the referenced element differs from the base address.

To implement this technique, we store the base type of each identifier in the identifier table. For example, consider

    arr: array [ 10 ] of integer ;
    x  : real ;
  

One Dimensional Arrays

Calculating the address of an element of a one dimensional array is easy. The address increment is the width of each element times the index (assuming indices start at 0). So the address of A[i] is the base address of A, which is the offset component of A's entry in the identifier table, plus i times the width of each element of A.

The width of each element is the width of what we have called the base type. So for an ID the element width is sizeof(getBaseType(ID.entry)). For convenience, we define getBaseWidth by the formula

        getBaseWidth(ID.entry) = sizeof(getBaseType(ID.entry)) = sizeof(ID.entry.baseType)

Two Dimensional Arrays

Let us assume row major ordering. That is, the first element stored is A[0,0], then A[0,1], ... A[0,k-1], then A[1,0], ... . Modern languages use row major ordering.

With the alternative column major ordering, after A[0,0] comes A[1,0], A[2,0], ... .

For two dimensional arrays the address of A[i,j] is the sum of three terms

1. The base address of A.
2. The distance from A to the start of row i. This is i times the width of a row, which is i times the number of elements in a row times the width of an element. The number of elements in a row is the column array bound.
3. The distance from the start of row i to element A[i,j]. This is j times the width of an element.

Remarks

1. Our grammar really declares one dimensional arrays of one dimensional arrays rather than 2D arrays. I believe this makes it easier.
2. The SDD above when processing the declaration
       A : array [5] of array [9] of real;
   gives A the type array(5,array(9,real)) and thus the type component of the entry for A in the symbol table contains all the values needed to compute the address of any given element of the array.

End of Remarks

Higher Dimensional Arrays

The generalization to higher dimensional arrays is clear.

A Simple Example

Consider the following expression containing a simple array reference, where a and c are integers and b is a real array.

    a = b[3*c]
  

    T1 = 3 * c     // i.e. mult T1,3,c
    T2 = T1 * 8    // each b[i] is size 8
    a  = b[T2]     // Uses the x[i] special form
  

    T1 = 3 * c
    T2 = T1 * 8
    T3 = &b
    T4 = T2 + T3
    a  = *T4
  

6.4.4: Translation of Array References

To include arrays we need to specify the semantic actions for the production
factor → IDENTIFIER indices

One-Dimensional Array References

As a warm-up, lets start with references to one-dimensional arrays. That is we consider instead of the above production, the simpler
factor → IDENTIFIER index

The table on the right does this in two ways, both with and without using the special addressing form x[i]. I included the version without a[i] for two reasons.

1. Since we are restricted to one dimensional arrays, the full code generation for the address of an element is not hard.
   
   
2. I thought it would be instructive to see the full address generation without hiding some of it under the covers.
   
   It was definitely instructive for me! Note that by avoiding the special form b=a[i], I ended up using two other special forms.
   
   Is there an easier way?

An Aside on Special Forms

Normally lisp is taught in our programming languages course, which is a prerequisite for compilers. If you no longer remember lisp, don't worry.

• In lisp there is a simple evaluation rule. To evaluate, for example, (a b c d) you
  1. Evaluate all four components.
  2. Confirm that the first component can evaluate to a function.
  3. Invoke this function passing as arguments the values calculated for the other three components.
• But this rule is not always applied!
• Instead there are special forms that are evaluated differently.
• For example (setq a b) does not evaluate a prior to invoking setq.
• A similar thing is happening with a[i]. It is a special form in that, unlike the normal rules for three-address code, we don't use the address of i but instead its value. Specifically the value of i is added to the address of a.

The rules for addresses in 3-address code also include

    a = &b
    a = *b
    *a = b
  

Let's carefully evaluate the simple example above

This is an exciting moment. At long last we really seem to be compiling!

Multidimensional Array References

As mentioned above in the general case we must process the production
f → IDENTIFIER indices

Following the method used in the 1D case we need to produce is.addr (is stands for indices). The basic idea is shown here

The Left-Hand Side

Now that we can evaluate expressions (including one-dimensional array reverences) we need to handle the left-hand side of an assignment statement (which also can be an array reference). Specifically we need semantic actions for the following productions from the lab3 grammar.
  id-statement   → ID rest-of-assign
  rest-of-assign → = expression ;
  rest-of-assign → indices = expression

Scalars and One Dimensional Arrays on the Left Hand Side

Once again we begin by restricting ourselves to one-dimensional arrays, which corresponds to replacing indices by index in the last production. The SDD for this restricted case is shown on the right.

Multi-dimensional Arrays on the Left Hand Side

The idea is the same as when a multidimensional array appears in an expression. Specifically,

1. Traverse the sub-tree routed at the top indices node and compute the total offset from the start of the array.
2. Multiply this offset by the width of each entry.
3. A[product] = RHS

Our Simple Example Revisited

Recall the program we could partially handle.

    procedure test () is
        y : integer;
        x : array [10] of real;
    begin
        y = 5;        // we haven't yet done statements
        x[2] = y;     // type error?
    end;
  

What about the possible type error?

1. We could ignore errors.
2. We could assume the intermediate language permits mismatched types. Final code generation would then need to generate conversion code or signal an error.
3. We could change the program to use only one type.
4. We could learn about type checking and conversions.

Let's take the last option.

Homework: What code is generated for the program written above?

6.5: Type Checking

Type Checking includes several aspects.

1. The language comes with a type system, i.e., a set of rules saying what types can appear where.
2. The compiler assigns a type expression to parts of the source program.
3. The compiler ensures that the type usage in the program conforms to the type system for the language. This does not mean that the necessary type checks are performed at compile time.

For any language, all type checking could be done at run time, i.e. there would be no compile-time checking. However, that does not mean the compiler is absolved from the type checking. Instead, the compiler generates code to do the checks at run time.

It is normally preferable to perform the checks at compile time, if possible. Some languages have very weak typing; for example, variables can change their type during execution. Often these languages need run-time checks. Examples include lisp, snobol, and apl.

A sound type system guarantees that all checks can be performed prior to execution. This does not mean that a given compiler will make all the necessary checks.

An implementation is strongly typed if compiled programs are guaranteed to run without type errors.

6.5.1: Rules for Type Checking

There are two forms of type checking.

1. We will learn type synthesis where the types of parts are used to infer the type of the whole. For example, integer+real=real.
2. Type inference is very slick. The type of a construct is determined from its usage. This permits languages like ML to check types even though names need not be declared.

We will implement type checking for expressions. Type checking statements is similar. The SDDs below (and for lab 4) contain type checking (and coercions) for assignment statements as well as expressions.

6.5.2: Type Conversions

A very strict type system would do no automatic conversion. Instead it would offer functions for the programmer to explicitly convert between selected types. Then either the program has compatible types or is in error. Such explicit conversions supplied by the programmer are called casts.

We, however, will consider a more liberal approach in which the language permits certain implicit conversions that the compiler is to supply. This is called type coercion.

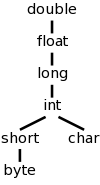
We continue to work primarily with the two basic types used in lab 3, namely integer and real, and postulate a unary function denoted (real) that converts an integer into the real having the same value. Nonetheless, we do consider the more general case where there are multiple types some of which have coercions (often called widenings). For example in C/Java, int can be widened to long, which in turn can be widened to float as shown in the figure to the right.

Mathematically the hierarchy on the right is a partially order set (poset) in which each pair of elements has a least upper bound (LUB). For many binary operators (all the arithmetic ones we are considering, but not exponentiation) the two operands are converted to the LUB. So adding a short to a char, requires both to be converted to an int. Adding a byte to a float, requires the byte to be converted to a float (the float remains a float and is not converted).

Checking and Coercing Types for Basic Arithmetic

The steps for addition, subtraction, multiplication, and division are all essentially the same: Convert each types if necessary to the LUB and then perform the arithmetic on the (converted or original) values. Note that conversion often requires the generation of code.

Two functions are convenient.

1. LUB(t1,t2) returns the type that is the LUB of the two given types. It signals an error if there is no LUB, for example if one of the types is an array.
2. widen(a,t,w,newcode,newaddr). Given an address a of type t, and a (hopefully) wider address w, produce the instructions newcode needed so that the address newaddr is the conversion of address a to type w.

LUB is simple, just look at the address latice. If one of the type arguments is not in the lattice, signal an error; otherwise find the lowest common ancestor. For our case the lattice is trivial, real is above int.

The widen function is more interesting. It involves n² cases for n types. Many of these are error cases (e.g., if t wider than w). Below is the code for our situation with two possible types integer and real. The four cases consist of 2 nops (when t=w), one error (t=real; w=integer) and one conversion (t=integer; w=real).

    widen (a:addr, t:type, w:type, newcode:string, newaddr:addr)
      if t=w
        newcode = ""
        newaddr = a
      else if t=integer and w=real
        newaddr = new Temp()
        newcode = gen(newaddr = (real) a)
      else signal error
  

With these two functions it is not hard to modify the rules to catch type errors and perform coercions for arithmetic expressions.

1. Maintain the type of each operand by defining type attributes for e, t, and f.
2. Coerce each operand to the LUB.

This requires that we have type information for the base entities, identifiers and numbers. The lexer can supply the type of the numbers. We retrieve it via get(NUM.type).

It is more interesting for the identifiers. We inserted that information when we processed declarations. So we now have another semantic check: Is the identifier declared before it is used?

I will use the function get(ID.type), which returns the type from the identifier table and signals an error if it is not there. The original SDD for expressions was here and the changes for (one-dimensional) arrays was here. We extended out treatment of expressions to include assignment statements by processing the LHS here

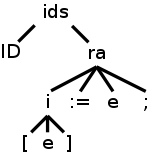
Before taking on the entire SDD, let's examine a particularly interesting entry
    identifier-statement → IDENTIFIER rest-of-assignment
and its right child
    rest-of-assignment → indices := expression ;.
Consider the assignment statement

    A[3/X+4] := X*5+Y;
  

    ra → i := e ;
  

Prior to doing its calculations, the ra node invokes its children and gets back all the synthesized attributes. Alternately said, when the tree traversal gets to this node the last time, the children have returned all the synthesized attributes. To summarize, when the ra node finally performs its calculations, it has available.

1. ra.id: the identifier entry for A.
   
   
2. i.addr/i.code: executing i.code results in i.addr containing the value of the index, i.e., the expression 3/X+4.
   
   
3. e.addr/e.code: executing e.code results in e.addr containing the value of the expression X*5+Y.
   
   
4. i.type/e.type: The types of the expressions.

What must the ra node do?

1. Ensure execution of i.code and e.code.
   
   
2. Check that i.type is int (I don't do this, but should/could).
   
   
3. Multiply i.addr by the base width of the array A. (We need a temporary, ra.t1, to hold the computed value).
   
   
4. Widen e to the base type of A. (We may need, and widen would then generates, a temporary ra.addr to hold the widened value).
   
   
5. Do the actual assignment of X*5+Y to A[3/X+4].

I hope the above illustration clarifies the semantic rules for the
    ra → i := e ;
production in the SDD on the right.

Because we are not considering multidimensional-arrays, the
    f → ID is
production (is abbreviates indices) is replaced by the two special cases corresponding to scalars and one-dimensional arrays, namely:
    f → ID     f → ID i

The above illustration should also help understanding the semantic rules for this last production.

Homework: Same question as the previous homework (What code is generated for the program written above?). But the answer is different!

6.6: Control Flow

A key to the understand of control flow is the study of Boolean expressions, which themselves are used in two roles.

1. They can be computed and treated similar to integers and realsf. In many programming languages once can declare Boolean variables, use the Boolean constants true and false, and construct larger Boolean expression using Boolean operators such as and and or. There are also relational operators that produce Boolean values from arithmetic operands. From this point of view, Boolean expressions are similar to the expressions we have already treated. Our previous semantic rules could be modified to generate the code needed to evaluate these expressions.
2. Boolean expressions are used in certain statements that alter the normal flow of control. It is in this regard that we have something new to learn.

6.6.1: Boolean Expressions

One question that comes up with Boolean expressions is whether both operands need be evaluated. If we are evaluating A or B and find that A is true, must we evaluate B? For example, consider evaluating

    A=0  OR  3/A < 1.2
  

This issue arises in other cases not involving Booleans at all. Consider A*F(x). If the compiler determines that A must be zero at this point, must it generate code to evaluate F(x)? Don't forget that functions can have side effects.

6.6.2: Short-Circuit (or Jumping) Code

Consider

    if bool-expr-1 OR bool-expr-2 then
        then-clause
    else
        else-clause
    end
  

When we compile the if condition bool-expr-1 OR bool-expr-2 we do not have an OR operator. Instead we just generate jumps to either the true branch or the false branch. We shall see that the above source code (with the simple bool-expr-1=x and bool-expr-2=y will generate

          if x goto L2
	  goto L1
     L1:
          if y goto L2
          goto l3
     L2:
	  then-clause-code
	  goto L4
     L3:
	  else-clause-code
     L4
  

Note that the compiled code does not evaluate y if x is true. This is the sense in which it is called short-circuit code. As we have stated above, for many programming languages, it is required that we not evaluate y if x is true.