Compilers

4.2.6: Verification

Skipped

4.2.7: Context-Free Grammars Versus Regular Expressions

Alternatively context-free languages vs regular languages.

Given an RE, construct an NFA as in chapter 3.

From that NFA construct a grammar as follows.

1. Define a nonterminal A_i for each state i.
2. For a transition from A_i to A_j on input a (or ε), add a production
   A_i → aA_j
3. If i is accepting, add A_i → ε
4. If i is start, make A_i start.

If you trace an NFA accepting a sentence, it just corresponds to the constructed grammar deriving the same sentence. Similarly, follow a derivation and notice that at any point prior to acceptance there is only one nonterminal; this nonterminal gives the state in the NFA corresponding to this point in the derivation.

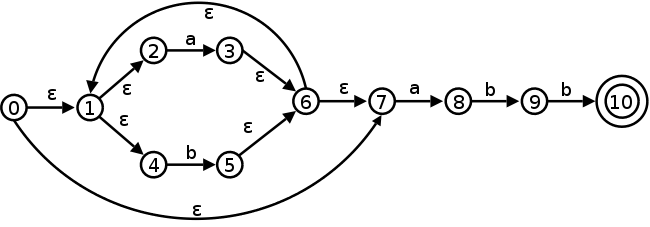
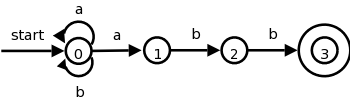
The book starts with (a|b)*abb and then uses the short NFA on the left below. Recall that the NFA generated by our construction is the longer one on the right.

The book gives the simple grammar for the short diagram.

Let's be ambitious and try the long diagram

    A0 → A1 | A7
    A1 → A2 | A4
    A2 → a A3
    A3 → A6
    A4 → b A5
    A5 → A6
    A6 → A1 | A7
    A7 → a A8
    A8 → b A9
    A9 → b A10
    A10 → ε
  

Now trace a path in the NFA and see that it is just a derivation. The same is true in reverse (derivation gives path). The key is that at every stage you have only one nonterminal.

Grammars, but not Regular Expressions, Can Count

The grammar

    A → a A b | ε
  

A proof is in the book. The idea is that you need a infinite number of states to represent the number of a's you have seen so that you can ensure that you see the same number of b's. But a RE is equivalent to a DFA (or NFA) and the F is for finite.

4.3: Writing a Grammar

4.3.1: Lexical vs Syntactic Analysis

Why have a separate lexer and parser?

1. As stated before, there are software engineering (modular programming) reasons.
   
   
2. The lexer deals with REs / Regular Languages.
   The parser deals with the more powerful Context Free Grammars (CFGs) / Context Free Languages (CFLs).
   • REs are easier than CFGs to understand.
   • More efficient algorithms/tools exist for automating the RE-based lexer than for the CFG-based parser.

4.3.2: Eliminating Ambiguity

Recall the ambiguous grammar with the notorious dangling else problem.

    stmt → if expr then stmt
         | if expr then stmt else stmt
         | other
  

This has two leftmost derivations for
if E1 then S1 else if E2 then S2 else S3

Do these on the board. They differ in the beginning.

In this case we can find a non-ambiguous, equivalent grammar.

        stmt → matched-stmt | open-stmt
matched-stmt → if expr then matched-stmt else matched-stmt
	     | other
   open-stmt → if expr then stmt
	     | if expr then matched-stmt else open-stmt
  

On the board find the unique parse tree for the problem sentence and from that the unique leftmost derivation.

Remark:
There are three areas relevant to the above example.

1. Language design. C vs Ada (end if). We are not studying this.
2. Finding a non-ambiguous grammar for the C if-then-else. This was not easy.
3. Parsing the dangling else example with the non-ambiguous grammar. We can do this.

4.3.3: Eliminating Left Recursion

We did special cases in chapter 2. Now we do it right(tm).

Previously we did it separately for one production and for two productions with the same nonterminal on the LHS. Not surprisingly, this can be done for n such productions (together with other non-left recursive productions involving the same nonterminal).

Specifically we start with

    A → A α1 | A α2 | ... A αn | β1 | β2 | ... βm
  

The equivalent non-left recursive grammar is

    A  → β1 A' | ... | βm A'
    A' → α1 A' | ... | αn A' | ε
  

The idea is as follows. Look at the left recursive grammar. At some point you stop producing more As and have the A (which is always on the left) become one of the βs. So the final string starts with a β. Up to this point all the As became Aα for one of the αs. So the final string is a β followed by a bunch of αs, which is exactly what the non-left recursive definition says.

Example: Assume n=m=1, α₁ is + and β₁ is *. With the recursive grammar, we have the following lm derivation.
A ⇒ A + ⇒ A + + ⇒ * + +
With the non-recursive grammar we have
A ⇒ * A' ⇒ * + A' ⇒ * + + A' ⇒ * + +

This removes direct left recursion where a production with A on the left hand side begins with A on the right. If you also had direct left recursion with B, you would apply the procedure twice.

The harder general case is where you permit indirect left recursion, where, for example one production has A as the LHS and begins with B on the RHS, and a second production has B on the LHS and begins with A on the RHS. Thus in two steps we can turn A into something starting again with A. Naturally, this indirection can involve more than 2 nonterminals.

Theorem: All left recursion can be eliminated.

Proof: The book proves this for grammars that have no ε-productions and no cycles and has exercises asking the reader to prove that cycles and ε-productions can be eliminated.

We will try to avoid these hard cases.

Homework: Eliminate left recursion in the following grammar for simple postfix expressions.
S → S S + | S S * | a

4.3.4: Left Factoring

If two productions with the same LHS have their RHS beginning with the same symbol (terminal or nonterminal), then the FIRST sets will not be disjoint so predictive parsing (chapter 2) will be impossible and more generally top down parsing (defined later this chapter) will be more difficult as a longer lookahead will be needed to decide which production to use.

So convert A → x y1 | x y2 into

   A  → x A'
   A' → y1 | y2
  

Homework: Left factor your answer to the previous homework.

4.3.5: Non-CFL Constructs

Although our grammars are powerful, they are not all-powerful. For example, we cannot write a grammar that checks that all variables are declared before used.

4.4: Top-Down Parsing

We did an example of top down parsing, namely predictive parsing, in chapter 2.

For top down parsing, we

1. Start with the root of the parse tree, which is always the start symbol of the grammar. That is, initially the parse tree is just the start symbol.
2. Choose a nonterminal in the frontier.
   1. Choose a production having that nonterminal as LHS.
   2. Expand the tree by making the RHS the children of the LHS.
3. Repeat above until the frontier is all terminals.
4. Hope that the frontier equals the input string.

The above has two nondeterministic choices (the nonterminal, and the production) and requires luck at the end. Indeed, the procedure will generate the entire language. So we have to be really lucky to get the input string.

Another problem is that the procedure may not terminate.

4.4.1: Recursive Decent Parsing

Let's reduce the nondeterminism in the above algorithm by specifying which nonterminal to expand. Specifically, we do a depth-first (left to right) expansion. This corresponds to a leftmost derivation. That is, we expand the leftmost non-terminal in the frontier.

We leave the choice of production nondeterministic.

We also process the terminals in the RHS, checking that they match the input. By doing the expansion depth-first, left to right, we ensure that we encounter the terminals in the order they will appear in the frontier of the final tree. Thus if the terminal does not match the corresponding input symbol now, it never will (since there are no nonterminals to its left) and the expansion so far will not produce the input string as desired.

Now our algorithm is

1. Initially, the tree is the start symbol, the nonterminal we are processing.
   
   
2. Choose a production having the current nonterminal A as LHS. Say the RHS is X1 X2 ... Xn.
   
   

3. for i = 1 to n
     if Xi is a nonterminal
       process Xi  // recursive
     else if Xi (a terminal) matches current input symbol
       advance input to next symbol
     else // trouble Xi doesn't match and never will
         

Note that the trouble mentioned at the end of the algorithm does not signify an erroneous input. We may simply have chosen the wrong production in step 2.

In a general recursive descent (top-down) parser, we would support backtracking. That is, when we hit the trouble, we would go back and choose another production. Since this is recursive, it is possible that no productions work for this nonterminal, because the wrong choice was made earlier.

The good news is that we will work with grammars where we can control the nondeterminism much better. Recall that for predictive parsing, the use of 1 symbol of lookahead made the algorithm fully deterministic, without backtracking.

4.4.2: FIRST and FOLLOW

We used FIRST(RHS) when we did predictive parsing.

Now we learn the whole truth about these two sets, which proves to be quite useful for several parsing techniques (and for error recovery, but we won't make use of this).

The basic idea is that FIRST(α) tells you what the first terminal can be when you fully expand the string α and FOLLOW(A) tells what terminals can immediately follow the nonterminal A.

Definition: For any string α of grammar symbols, we define FIRST(α) to be the set of terminals that occur as the first symbol in a string derived from α. So, if α⇒*cβ for c a terminal and β a string, then c is in FIRST(α). In addition, if α⇒*ε, then ε is in FIRST(α).

Definition: For any nonterminal A, FOLLOW(A) is the set of terminals x, that can appear immediately to the right of A in a sentential form. Formally, it is the set of terminals c, such that S⇒*αAcβ. In addition, if A can be the rightmost symbol in a sentential form (i.e., if S⇒*αA), the endmarker $ is in FOLLOW(A).

Note that there might have been symbols between A and c during the derivation, providing they all derived ε and eventually c immediately follows A.

Unfortunately, the algorithms for computing FIRST and FOLLOW are not as simple to state as the definition suggests, in large part caused by ε-productions.

1. FIRST(a)={a} for all terminals a.
2. Initialize FIRST(A)=φ for all nonterminals A
3. If A → ε is a production, add ε to FIRST(A).
4. For each production A → Y₁ ... Y_n,
   1. add to FIRST(A) any terminal a satisfying
      1. a is in FIRST(Y_i) and
      2. ε is in all previous FIRST(Y_j).
   2. add ε to FIRST(A) if ε is in all FIRST(Y_j).
   Repeat this entire step until nothing is added.
5. FIRST of any string X=X₁X₂...X_n is initialized to φ and then
   1. add to FIRST(X) any non-ε symbol in FIRST(X_i) if ε is in all previous FIRST(X_j).
   2. add ε to FIRST(X) if ε is in every FIRST(X_j). In particular if X is ε, FIRST(X)={ε}.
6. Initialize FOLLOW(S)=$ and FOLLOW(A)=φ for all other nonterminals A, and then apply the following three rules until nothing is added to any FOLLOW set.
   1. For every production A → α B β, add all of FIRST(β) except ε to FOLLOW(B).
   2. For every production A → α B, add all of FOLLOW(A) to FOLLOW(B).
   3. For every production A → α B β where FIRST(β) contains ε, add all of FOLLOW(A) to FOLLOW(B).

Do the FIRST and FOLLOW sets for

    E  → T E'
    E' → + T E' | ε
    T  → F T'
    T' → * F T' | ε
    F  → ( E ) | id