Computer Architecture

Start Lecture #22

7.3: Measuring and Improving Cache Performance

Do the following performance example on the board. It would be an appropriate final exam question.

• Assume
  • 5% I-cache misses.
  • 10% D-cache misses.
  • 1/3 of the instructions access data.
  • The CPI = 4 if the miss penalty is 0. A 0 miss penalty is not realistic of course.
• What is the CPI if the miss penalty is 12?
• What is the CPI if we upgrade to a double speed cpu+cache, but keep a single speed memory (i.e., a 24 clock miss penalty)?
• How much faster is the double speed machine? It would be double speed if the miss penalty were 0 or if there was a 0% miss rate.

Homework: 7.17, 7.18.

A lower base (i.e. miss-free) CPI makes stalls appear more expensive since waiting a fixed amount of time for the memory corresponds to losing more instructions if the CPI is lower.

A faster CPU (i.e., a faster clock) makes stalls appear more expensive since waiting a fixed amount of time for the memory corresponds to more cycles if the clock is faster (and hence more instructions since the base CPI is the same).

Another performance example.

• Assume
  1. I-cache miss rate 3%.
  2. D-cache miss rate 5%.
  3. 40% of instructions reference data.
  4. miss penalty of 50 cycles.
  5. Base CPI is 2.
• What is the CPI including the misses?
• How much slower is the machine when misses are taken into account?
• Redo the above if the I-miss penalty is reduced to 10 (D-miss still 50)
• With I-miss penalty back to 50, what is performance if CPU (and the caches) are 100 times faster

Remark: Larger caches have longer hit times.

Reducing Cache Misses by More Flexible Placement of Blocks

Improvement: Associative Caches

Consider the following sad story. Jane has a cache that holds 1000 blocks and has a program that only references 4 (memory) blocks, namely 23, 1023, 123023, and 7023. In fact the references occur in order: 23, 1023, 123023, 7023, 23, 1023, 123023, 7023, 23, 1023, 123023, 7023, 23, 1023, 123023, 7023, etc. Referencing only 4 blocks and having room for 1000 in her cache, Jane expected an extremely high hit rate for her program. In fact, the hit rate was zero. She was so sad, she gave up her job as webmistress, went to medical school, and is now a brain surgeon at the mayo clinic in rochester MN.

So far We have studied only direct mapped caches, i.e. those for which the location in the cache is determined by the address. Since there is only one possible location in the cache for any block, to check for a hit we compare one tag with the HOBs of the addr.

The other extreme is fully associative.

• A memory block can be placed in any cache block.
• Since any memory block can be in any cache block, the cache index where the memory block is stored tells us nothing about which memory block is stored there. Hence the tag must be the entire address. Moreover, we don't know which cache block to check so we must check all cache blocks to see if we have a hit.
• The larger tag is a problem.
• The search is a disaster.
  • It could be done sequentially (one cache block at a time), but this is much too slow.
  • We could have a comparator with each tag and mux all the blocks to select the one that matches.
    • This is too big due to both the many comparators and the humongous mux.
    • However, it is exactly what is done when implementing translation lookaside buffers (TLBs), which are used with demand paging.
    • Are the TLB designers magicians?
      Ans: No. TLBs are small.
• An alternative is to have a table with one entry per memory block telling if the memory block is in the cache and if so giving the cache block number. This is too big and too slow for caches but is exactly what is used for virtual memory (demand paging) where the memory blocks here correspond to pages on disk and the table is called the page table.

Set Associative Caches

Most common for caches is an intermediate configuration called set associative or n-way associative (e.g., 4-way associative). The value of n is typically 2, 4, or 8.

If the cache has B blocks, we group them into B/n sets each of size n. Since an n-way associative cache has sets of size n blocks, it is often called a set size n cache. For example, you often hear of set size 4 caches.

In a set size n cache, memory block number K is stored in set K mod the number of sets, which equals K mod (B/n).

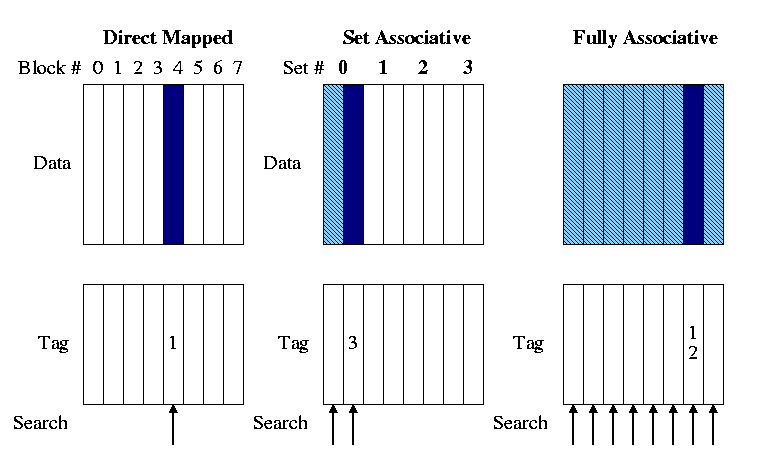
• In the picture on the right we are trying to store memory block 12 in each of three caches.
• Figure 7.13 in the book, from which my figure was taken, has a bug. Figure 7.13 indicates that the tag for memory block 12 is 12 for each associativity. The figure to the right corrects this.
• The light blue represents cache blocks in which the memory block might have been stored.
• The dark blue is the cache block in which the memory block is stored.
• The arrows show the blocks (i.e., tags) that must be searched to look for memory block 12. Naturally the arrows point to the blue blocks.

The figure above shows a 2-way set associative cache. Do the same example on the board for 4-way set associative.

Determining the Set Number and the Tag.

Recall that for the a direct-mapped cache, the cache index gives the number of the block in the cache. The for a set-associative cache, the cache index gives the number of the set.

Just as the block number for a direct-mapped cache is the memory block number mod the number of blocks in the cache, the set number equals the (memory) block number mod the number of sets.

Just as the tag for a direct mapped cache is the memory block number divided by the number of blocks, the tab for a set-associative cache is the memory block number divided by the number of sets.

Do NOT make the mistake of thinking that a set size 2 cache has 2 sets, it has B/2 sets each of size 2.

Ask in class.

• What is another name for an 8-way associative cache having 8 blocks?
• What is another name for a 1-way set associative cache?

Why is set associativity good? For example, why is 2-way set associativity better than direct mapped?

• Consider referencing two arrays of size 50K that start at location 1MB and 2MB.
• Both will contend for the same cache locations in a direct mapped 128K cache but will fit together in any 128K n-way associative cache with n>=2.

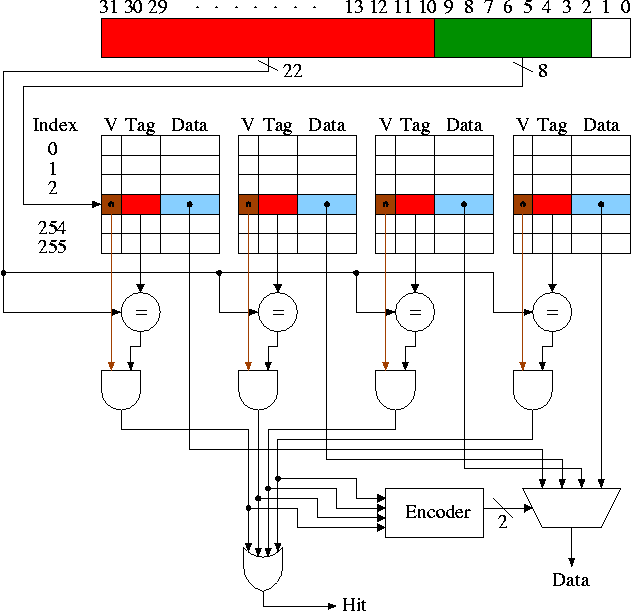
Locating a Block in the Cache

How do we find a memory block in a set associative cache with block size 1 word?

• Divide the memory block number by the number of sets to get the tag. This portion of the address is shown in red in the diagram.
• Mod the memory block number by the number of sets to get the tag. This portion of the address is shown in green.
• Check all the tags in the set against the tag of the memory block.
• If any tag matches, a hit has occurred and the corresponding data entry contains the memory block.
• If no tag matches, a miss has occurred.

Recall that a 1-way associative cache is a direct mapped cache and that an n-way associative cache for n the number of blocks in the cache is a fully associative.

The advantage of increased associativity is normally an increased hit ratio.

What are the disadvantages?
Answer: It is a slower and a little bigger due to the extra logic.

Choosing Which Block to Replace

When an existing block must be replaced, which victim should we choose? We ask the exact same question (with different words) when we study demand paging (remember 202!).

• The victim must be in the same set as the new block. With direct mapped (1-way associative) caches, this determined the victim so the question didn't arise.
• With a fully associative cache all resident blocks are candidate victims. This is exactly the situation for demand paging (with global replacement policies) and is also the case for (fully-associative) TLBs.
• Random is sometimes used, i.e. choose a random block in the set as the victim.
  • This is never done for demand paging.
  • For caches, however, the number of blocks in a set is small, so the likely difference in quality between the best and the worst is less.
  • For caches, speed is crucial so we have no time for calculations, even for misses.
• LRU is better, but is not easy to do quickly.
  • If the cache is 2-way set associative, each set is of size two and it is easy to find the lru block quickly. How?
    Ans: For each set keep a bit indicating which block in the set was just referenced and the lru block is the other one.
  • If the cache is 4-way set associative, each set is of size 4. Consider these 4 blocks as two groups of 2. Use the trick above to find the group most recently used and pick the other group. Also use the trick within each group and chose the block in the group not used last.
  • Sound great. We can do lru fast for any power of two using a binary tree.
  • Wrong! The above is not LRU it is just an approximation. Show this on the board.

Sizes

There are two notions of size.

1. The cache size is the capacity of the cache.
   This means, the size of all the blocks. In the diagram above it is the size of the blue portion.

   The size of the cache in the diagram is 256 * 4 * 4B = 4KB.

2. Another size is is the total number of bits in the cache, which includes tags and valid bits. For the diagram this is computed as follows.
   • The 32 address bits contain 8 bits of index and 2 bits giving the byte offset.
   • So the tag is 22 bits (more examples just below).
   • Each block contains 1 valid bit, 22 tag bits and 32 data bits, for a total of 55 bits.
   • There are 1K blocks.
   • So the total size is 55Kb (kilobits).

For the diagrammed cache, what fraction of the bits are user data?
Ans: 4KB / 55Kb = 32Kb / 55Kb = 32/55.

Tag Size and Division of the Address Bits

We continue to assume a byte addressed machines with all references to a 4-byte word.

The 2 LOBs are not used (they specify the byte within the word, but all our references are for a complete word). We show these two bits in dark blue. We continue to assume 32 bit addresses so there are 2³⁰ words in the address space.

Let's review various possible cache organizations and determine for each how large is the tag and how the various address bits are used. We will consider four configurations each a 16KB cache. That is the size of the data portion of the cache is 16KB = 4 kilowords = 2¹² words.

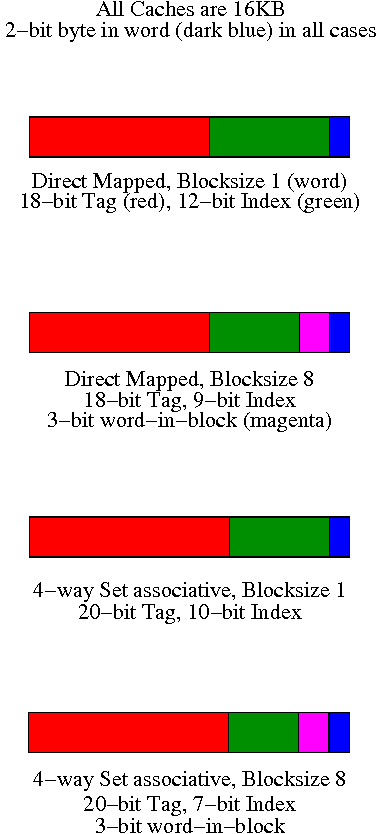
1. Direct mapped, blocksize 1 (word).
   • Since the blocksize is one word, there are 2³⁰ memory blocks and all the address bits (except the blue 2 LOBs that specify the byte within the word) are used for the memory block number. Specifically 30 bits are so used.
   • The cache has 2¹² words, which is 2¹² blocks.
   • So the low order 12 bits of the memory block number give the index in the cache (the cache block number), shown in green.
   • The remaining 18 (30-12) bits are the tag, shown in red.
   
   
2. Direct mapped, blocksize 8
   • Three bits of the address give the word within the 8-word block. These are drawn in magenta.
   • The remaining 27 HOBs of the memory address give the memory block number.
   • The cache has 2¹² words, which is 2⁹ blocks.
   • So the low order 9 bits of the memory block number gives the index in the cache.
   • The remaining 18 bits are the tag
   
   
3. 4-way set associative, blocksize 1
   • Blocksize is 1 so there are 2³⁰ memory blocks and 30 bits are used for the memory block number.
   • The cache has 2¹² blocks, which is 2¹⁰ sets (each set has 4=2² blocks).
   • So the low order 10 bits of the memory block number gives the index in the cache.
   • The remaining 20 bits are the tag.
   • As the associativity grows, the tag gets bigger. Why?
     Ans: Growing associativity reduces the number of sets into which a block can be placed. This increases the number of memory blocks eligible to be placed in a given set. Hence more bits are needed to see if the desired block is there.
   
   
4. 4-way set associative, blocksize 8
   • Three bits of the address give the word within the block.
   • The remaining 27 HOBs of the memory address give the memory block number.
   • The cache has 2¹² words = 2⁹ blocks = 2⁷ sets.
   • So the low order 7 bits of the memory block number gives the index in the cache.
   • The remaining 20 bits form the tag.

Homework: 7.46 and 7.47. Note that 7.46 contains a typo !! should be ||.

Reducing the Miss Penalty Using Multilevel Caches

Improvement: Multilevel caches

Modern high end PCs and workstations all have at least two levels of caches: A very fast, and hence not very big, first level (L1) cache together with a larger but slower L2 cache.

When a miss occurs in L1, L2 is examined and only if a miss occurs there is main memory referenced.

So the average miss penalty for an L1 miss is

    (L2 hit rate)*(L2 time) + (L2 miss rate)*(L2 time + memory time)
  

We are assuming that L2 time is the same for an L2 hit or L2 miss and that the main memory access doesn't begin until the L2 miss has occurred.

Do the example on the board (a reasonably exam question, but a little long since it has so many parts).

• Assume
  1. L1 I-cache miss rate 4%
  2. L1 D-cache miss rate 5%
  3. 40% of instructions reference data
  4. L2 miss rate 6%
  5. L2 time of 15ns
  6. Memory access time 100ns
  7. Base CPI of 2
  8. Clock rate 400MHz
• How many instructions per second does this machine execute?
• How many instructions per second would this machine execute if the L2 cache were eliminated?
• How many instructions per second would this machine execute if both caches were eliminated?
• How many instructions per second would this machine execute if the L2 cache had a 0% miss rate (L1 as originally specified)?
• How many instructions per second would this machine execute if both L1 caches had a 0% miss rate?