Computer Architecture

Start Lecture #21

Remark: Demo of tristate drivers in logisim (controlled registers).

Improvement: Multiword Blocks

The setup we have described does not take any advantage of spatial locality. The idea of having a multiword block size is to bring into the cache words near the referenced word since, by spatial locality, they are likely to be referenced in the near future.

We continue to assume (for a while) that the cache is direct mapped and that all references are for one word.

The terminology for byte offset and block offset is inconsistent. The byte offset gives the offset of the byte within the word so the offset of the word within the block should be called the word offset, but alas it is not in both the 2e and 3e. I don't know if this is standard (poor) terminology or a long standing typo in both editions.

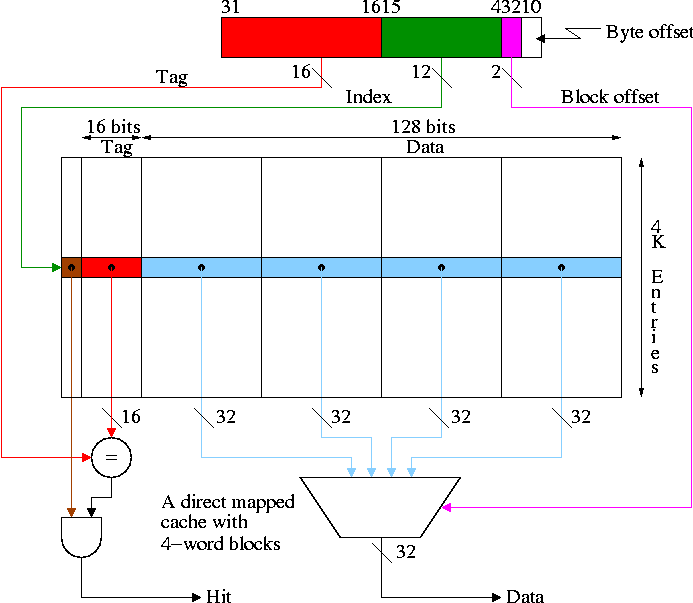
The figure to the right shows a 64KB direct mapped cache with 4-word blocks.

What addresses in memory are in the block and where in the cache do they go?

• The word address = the byte address / number of bytes per word = the byte address / 4
  for the 4-byte words we are assuming.
• The memory block number = the word address / number of words per block =
  the byte address / number of bytes per block.
• The cache block number = the memory block number modulo the number of blocks in the cache.
• The block offset (i.e., word offset) = the word address modulo the number of words per block.
• The tag = the memory block number / the number of blocks in the cache =
  the word address / the number of words in the cache = the byte address / the number of bytes in the cache

Show from the diagram how this gives the red portion for the tag and the green portion for the index or cache block number.

Consider the cache shown in the diagram above and a reference to word 17003.

• 17003 / 4 gives 4250 with a remainder of 3 .
• So the memory block number is 4250 and the block offset is 3.
• 4K=4096 and 4250 / 4096 gives 1 with a remainder of 154.
• So the cache block number is 154 and the tag is 1.
• Summary: Memory word 17003 resides in word 3 of cache block 154 with tag 154 set to 1.

The cache size is the size of the data portion of the cache (normally measured in bytes).

For the caches we have see so far this is the Blocksize times the number of entries. For the diagram above this is 64KB. For the simpler direct mapped caches blocksize = wordsize so the cache size is the wordsize times the number of entries.

Let's compare the pictured cache with another one containing 64KB of data, but with one word blocks.

1. Calculate on the board the total number of bits in each cache; this is not simply 8 times the cache size in bytes.
2. If the references are strictly sequential the pictured cache has 75% hits; the simpler cache with one word blocks has no hits.

How do we process read/write hits/misses for a cache with multiword blocks?

• Read hit: As before, return the data found to the processor.
• Read miss: As before, due to locality we discard (or write back depending on the policy) the old line and fetch the new line.
• Write hit: As before, write the word in the cache (and perhaps write memory as well depending on the policy).
• Write miss: A new consideration arises. As before we might or might not decide to replace the current line with the referenced line and, if we do decide to replace the line, we might or might not have to write the old line back. The new consideration is that if we decide to replace the line (i.e., if we are implementing store-allocate), we must remember that we only have a new word and the unit of cache transfer is a multiword line.
  • The simplest idea is to fetch the entire old line and overwrite the new word. This is called write-fetch and is something you wouldn't even consider with blocksize = reference size = 1 word. Why?
    Answer: You would be fetching the one word that you want to replace so you would fetch and then discard the entire fetched line.
  • Why, with multiword blocks, do we fetch the whole line including the word we are going to overwrite?
    Answer. The memory subsystem probably can't fetch just words 1,2, and 4 of the line.
  • Why might we want store-allocate and write-no-fetch?
    
  • Ans: Because a common case is storing consecutive words: With store-no-allocate all are misses and with write-fetch, each store fetches the line to overwrite another part of it.
  • To implement store-allocate-no-write-fetch (SANF), we need to keep a valid bit per word.

Homework: 7.9, 7.10, 7.12.

Why not make blocksize enormous? For example, why not have the cache be one huge block.

• NOT all access are sequential.
• With too few blocks misses go up again.

Memory support for wider blocks

Recall that our processor fetches one word at a time and our memory produces one word per request. With a large blocksize cache the processor still requests one word and the cache responds with one word. However the cache requests a multiword block from memory and to date our memory is only able to respond with a single word.

The question is, "Which pieces and buses should be narrow (one word) and which ones should be wide (a full block)?". The same question arises when the cache requests that the memory store a block and the answers are the same so we will only consider the case of reading the memory).

• Should memory be wide? That is, should the memory have enough pins so that the entire block is produced at once.
• Should the bus from the cache to the processor be wide? Since the processor is only requesting a single word, a wide cache to processor bus seems silly. The processor would contain a mux to discard the other words (you could imagine a buffer to store the entire block acting as a kind of L0 cache, but this would not be so useful if the L1 cache was fast enough).
• Assume
  1. 1 clock required to send the address. This is valid since only one address is needed per access for all designs.
  2. 15 clocks are required for each memory access (independent of width). Today the number would likely be bigger than 15, but it would remain independent of the width
  3. 1 Clock is required to transfer each busload of data.
• How long does it take satisfy a read miss for the cache above and each of the three memory/bus systems.
• The narrow design (a) takes 65 clocks: 1 address transfer, 4 memory reads, 4 data transfers (do it on the board).
• The wide design (b) takes 17.
• The interleaved design (c) takes 20.
• Interleaving works great because in this case we are guaranteed to have sequential accesses.
• Imagine a design between (a) and (b) with a 2-word wide datapath.
  It takes 33 cycles and is more expensive to build than (c).

Homework: 7.14