Computer Architecture

Start Lecture #16

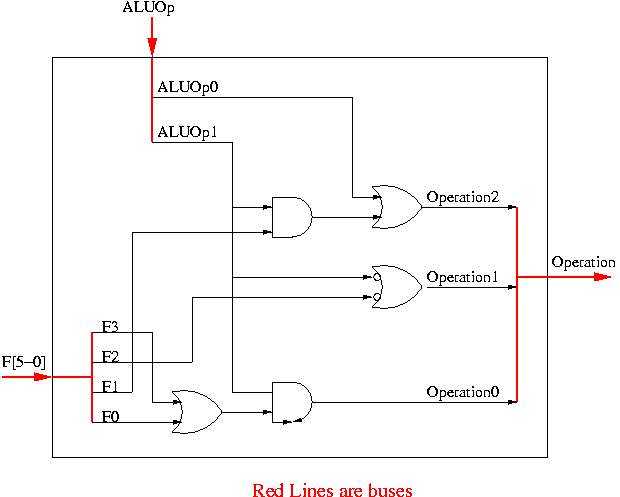
How should we implement this?
We will do it PLA style (disjunctive normal form, 2-levels of logic).

• Produce a circuit for each of the three output bits.
• Must decide when each output bit is 1, i.e., calculate the minterms.
• We do this one output bit at a time.

When is Bnegate (called Op2 in book) asserted?
Ans: Those rows where its bit is 1, namely rows 2, 4, and 7.

    ALUOp | Funct
    1 0   | 5 4 3 2 1 0
    ------+------------
    x 1   | x x x x x x
    1 x   | x x 0 0 1 0
    1 x   | x x 1 0 1 0
  

Notice that, in the 5 rows with ALUOp=1x, F1=1 is enough to distinugish the two rows where Bnegate is asserted. This gives

    ALUOp | Funct
    1 0   | 5 4 3 2 1 0
    ------+-------------
    x 1   | x x x x x x
    1 x   | x x x x 1 x
  

Hence Bnegate is ALUOp0 + (ALUOp1 F1)

Now we apply the same technique to determine when is OP0 asserted and begin by listing the rows where its bit is set.

    ALUOp | Funct
    1 0   | 5 4 3 2 1 0
    ------+------------
    1 x   | x x 0 1 0 1
    1 x   | x x 1 0 1 0
  

    ALUOp | Funct
    1 0   | 5 4 3 2 1 0
    ------+------------
    1 x   | x x x x x 1
    1 x   | x x 1 x x x
  

So OP0 is ALUOp1 F0 + ALUOp1 F3

Finally, we determine when is OP1 asserted and once again begin by listing the rows where its bit is one.

    ALUOp | Funct
    1 0   | 5 4 3 2 1 0
    ------+------------
    0 0   | x x x x x x
    x 1   | x x x x x x
    1 x   | x x 0 0 0 0
    1 x   | x x 0 0 1 0
    1 x   | x x 1 0 1 0
  

Inspection of the 5 rows with ALUOp=1x yields one F bit that distinguishes when OP1 is asserted, namely F2=0. Is this good luck, or well chosen funct values, or wise subset selection by H&P?

    ALUOp | Funct
    1 0   | 5 4 3 2 1 0
    ------+------------
    0 0   | x x x x x x
    x 1   | x x x x x x
    1 x   | x x x 0 x x
  

Since x 1 in the second row is really 0 1, rows 1 and 2 can be combined to give

	ALUOp | Funct
	1 0   | 5 4 3 2 1 0
	------+------------
	0 x   | x x x x x x
	1 x   | x x x 0 x x
      

Now we can use the first row to enlarge the scope of the last row

	ALUOp | Funct
	1 0   | 5 4 3 2 1 0
	------+------------
	0 x   | x x x x x x
	x x   | x x x 0 x x
      

So OP1 = NOT ALUOp1 + NOT F2

The circuit is then easy and is shown on the right.

The Main Control

Our task, illustrated in the diagram below, is to calculate 9 bits, specifically:

• Setting the four muxes.
• Writing the registers.
• Writing the memory.
• Reading the memory (for technical reasons, would not be needed if the memory was built from registers).
• Calculating ALUOp.

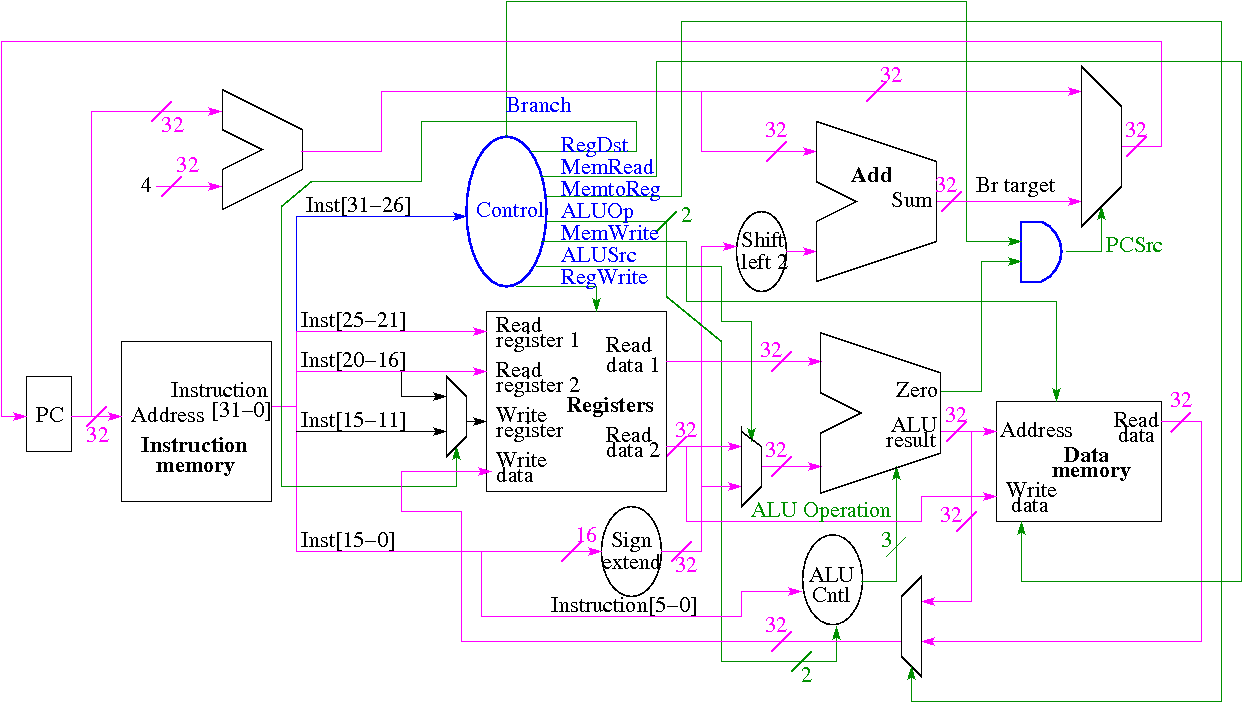
All 9 bits are determined by the opcode. We show the logic diagram after we illustrate the operation of the control logic.

Note that the MIPS instruction set is fairly regular. Most of the fields we need are always in the same place in the instruction (independent of the instruction type).

• The opcode (called Op[5-0]) is always in 31-26.
• The registers to be read are always 25-21 and 20-16 (R-type, beq, store).
• The base register used for calculating the effective address is always 25-21 (load store).
• The offset used for calculating the effective address is the immediate field, which is always 15-0.
• Oops: The register to be written is sometimes 20-16 (load) and other times 15-11 (R-type). Hence a mux is needed

MemRead:	Memory delivers the value stored at the specified addr
MemWrite:	Memory stores the specified value at the specified addr
ALUSrc:	Second ALU operand comes from (reg-file / sign-ext-immediate)
RegDst:	Number of reg to write comes from the (rt / rd) field
RegWrite:	Reg-file stores the specified value in the specified register
PCSrc:	New PC is Old PC+4 / Branch target
MemtoReg:	Value written in reg-file comes from (alu / mem)

We have just seen how to calculate ALUOp, the remaining 7 bits (recall that ALUOp is 2 bits) are described in the table to the right and their uses in controlling the datapath is shown in the picture above.

We are interested in four opcodes.

• R-type
• load
• store
• BEQ

Do a stage play

• Need volunteers
  1. One for each of 4 muxes
  2. One for PC reg
  3. One for the register file
  4. One for the instruction memory
  5. One for the data memory
• I will play the control
• Let the PC initially be zero
• Let each register initially contain its number (e.g. R2=2)
• Let each data memory word initially contain 100 times its address
• Let the instruction memory contain (starting at zero)

  	add r9,r5,r1 r9=r5+r1   0   5   1   9   0  32
  	sub r9,r9,r6            0   9   6   9   0  34
  	beq r9,r0,-8            4   9   0   <  -2   >
  	slt r1,r9,r0            0   9   0   1   0  42
  	lw  r1,102(r2)         35   2   1   <  100  >
  	sw  r9,102(r2)
        

• Go!

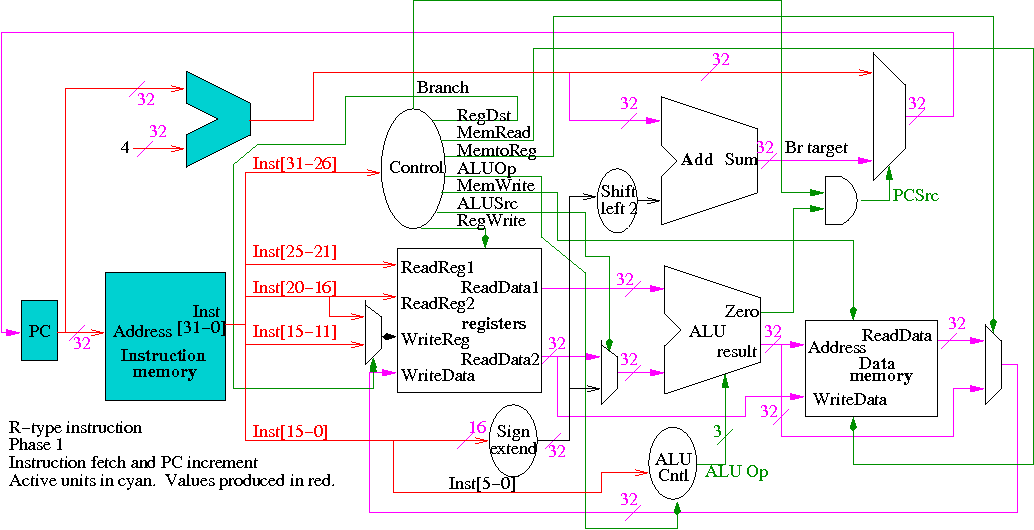
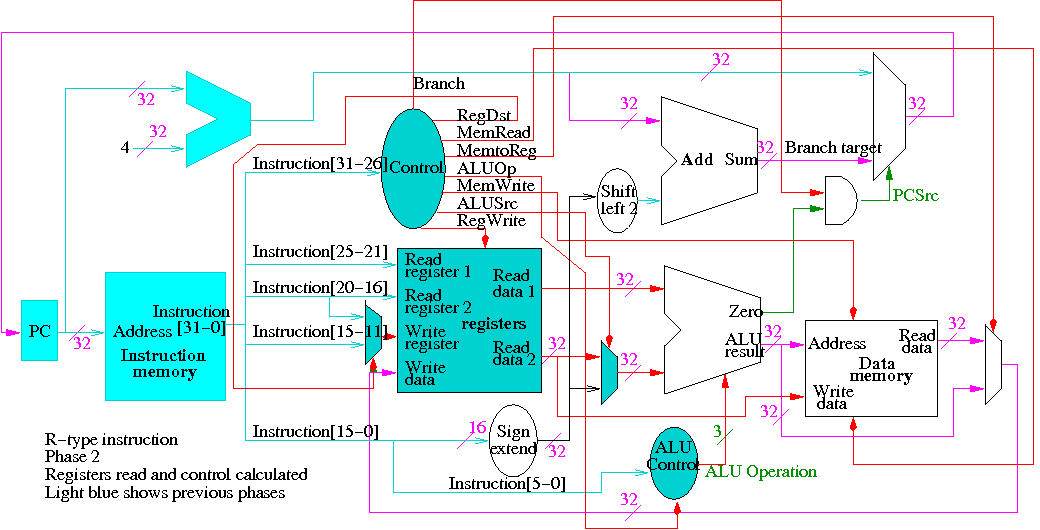
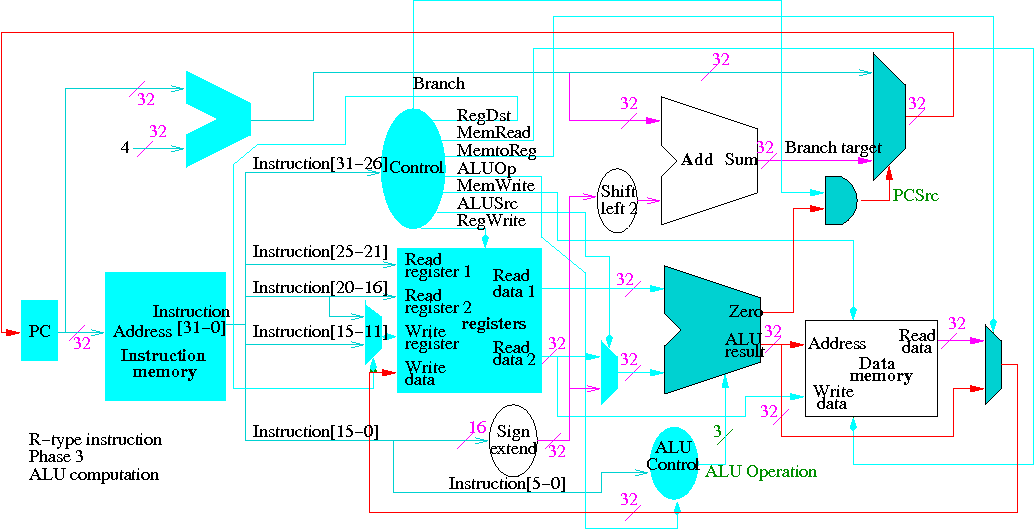
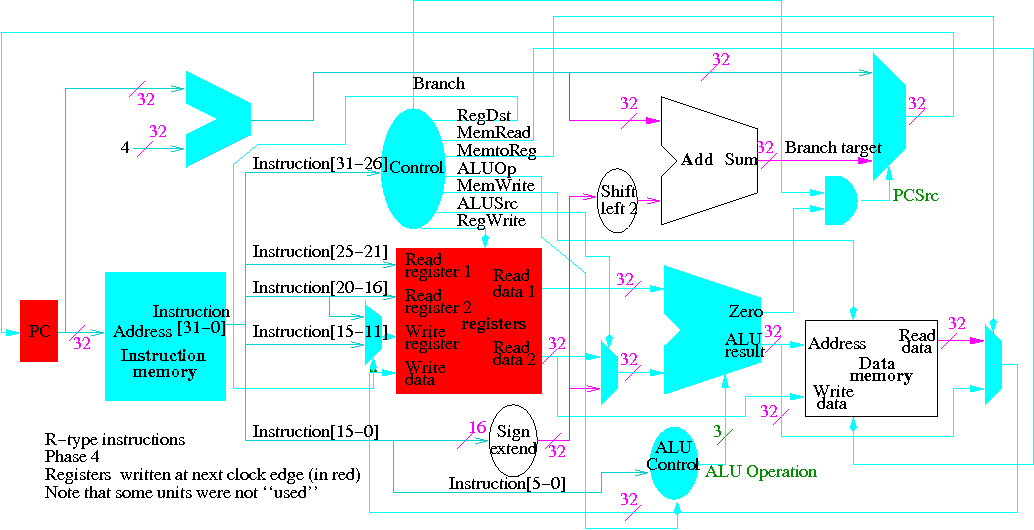
The following figures illustrate the play.

We start with R-type instructions