Computer Architecture

Start Lecture #11

Homework: Read 3.1-3-4

3.1: Introduction

I have nothing to add.

3.2: Signed and Unsigned Numbers

MIPS uses 2s complement (just like 8086)

To form the 2s complement (of 0000 1111 0000 1010 0000 0000 1111 1100)

• Take the 1s complement.
• That is, complement each bit (1111 0000 1111 0101 1111 1111 0000 0011)
• Then add 1 (1111 0000 1111 0101 1111 1111 0000 0100)

Need comparisons for signed and unsigned.

• For signed a leading 1 is smaller (negative) than a leading 0
• For unsigned a leading 1 is larger than a leading 0

Comments on Two's Complement

You could easily ask what does this funny notation have to do with negative numbers. Let me make a few comments.

1. What does minus 1 mean?
   Ans: It is the unique number that, when added to 1, gives zero.
2. The binary number 1111...1111 has this property (using regular n-bit addition and discarding the carry-out) so we do seem to have -1 correct.
3. Just as n+1 (for n≥0) is defined as the successor of n, -(n+1) is the number that has -n as successor. That is we need to show that
   TwosComp(n+1) + 1 = TwosComp(n).
4. This would follow if we coud show
   OnesComp(n+1) + 1 = OnesComp(n), i.e, (n+1)' + 1 = n'.
   1. Let n be even, n = *0, * arbitrary.
   2. Write n', n+1 and (n+1)' and see that it works.
   3. Let n be odd, n = *01^s1, where 1^s just means a bunch of ones.
   4. Again it works.
5. So for example TwosComp(6)+1=TwosComp(5) and hence TwosComp(6)+6=zero, so it really is -6.

sltu and sltiu

Like slt and slti but the comparison is unsigned.

Homework: 3.1-3.6

3.3: Addition and subtraction

To add two (signed) numbers just add them. That is, don't treat the sign bit special.

To subtract A-B, just take the 2s complement of B and add.

An overflow occurs when the result of an operation cannot be represented with the available hardware. For MIPS this means when the result does not fit in a 32-bit word.

• We have 31 bits plus a sign bit.
• The result would definitely fit in 33 bits (32 plus sign)
• The hardware simply discards the carry out of the top (sign) bit
• This is not wrong--consider -1 + -1

          11111111111111111111111111111111   (32 ones is -1)
        + 11111111111111111111111111111111
        ----------------------------------
         111111111111111111111111111111110   Now discard the carry out
  
          11111111111111111111111111111110   this is -2
        

• The bottom 31 bits are always correct.
  Overflow occurs when the 32 (sign) bit is set to a value and not the sign.
• Here are the conditions for overflow

          Operation  Operand A  Operand B  Result
          A+B         ≥ 0          ≥ 0       < 0
          A+B         < 0          < 0       ≥ 0
          A-B         ≥ 0          < 0       < 0
          A-B         < 0          ≥ 0       ≥ 0
        

• These conditions are the same as
  Carry-In to sign position != Carry-Out

Homework: Prove this last statement (4.29) (for fun only, do not hand in).

addu, subu, addiu

These three instructions perform addition and subtraction the same way as do add and sub, but do not signal overflow.

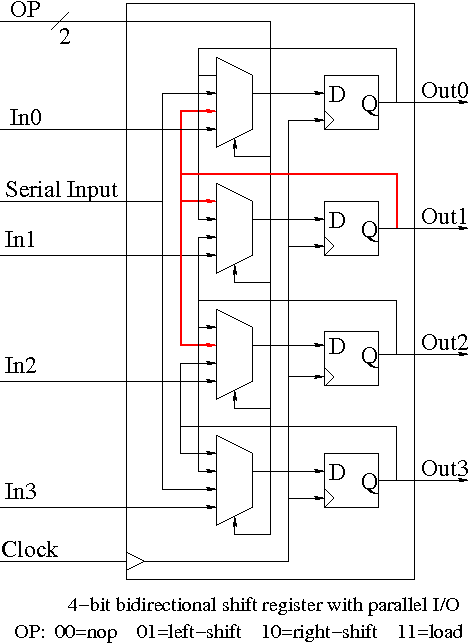
Shifter

This is a sequential circuit.

• Just a string of D-flops; output of one is input of next
  • Input to first is the serial input.
  • Output of last is the serial output.
  
  
• We want more.
  1. Left and right shifting (with serial input/output).
  2. Parallel load.
  3. Parallel Output.
  4. Don't shift every cycle.
  
  
• Parallel output is just wires.
  
  
• Shifter has 4 modes (left-shift, right-shift, nop, load) so
  • 4-1 mux inside.
  • 2 select lines are needed.
  
  
• We could modify our registers to be shifters (bigger mux), but ...
  
  
• Our shifters are slow for big shifts; barrel shifters are better and kept separate from the processor registers.

Homework: A 4-bit shift register initially contains 1101. It is shifted six times to the right with the serial input being 101101. What is the contents of the register after each shift.

Homework: Same register, same initial condition. For the first 6 cycles the opcodes are left, left, right, nop, left, right and the serial input is 101101. The next cycle the register is loaded (in parallel) with 1011. The final 6 cycles are the same as the first 6. What is the contents of the register after each cycle?

3.4: Multiplication

Of course we can do this with two levels of logic since multiplication is just a function of its inputs.

But just as with addition, would have a very big circuit and large fan in. Instead we use a sequential circuit that mimics the algorithm we all learned in grade school.

Recall how to do multiplication.

• Multiplicand times multiplier gives product
• Multiply multiplicand by each digit of multiplier
• Put the result in the correct column
• Then add the partial products just produced

We will do it the same way ...
... but differently

• We are doing binary arithmetic so each digit of the multiplier is 1 or zero.
• Hence multiplying the mulitplicand by a digit of the multiplier means either
  • Getting the multiplicand
  • Getting zero
• Use an if appropriate bit of multiplier is 1 stmt
  
• To get the appropriate bit
  • Start with the LOB of the multiplier
  • Shift the multiplier right (so the next bit is the LOB)
• Putting in the correct column means putting it one column further left than the last time.
• This is done by shifting the multiplicand left one bit each time (even if the multiplier bit is zero).
• Instead of adding partial products at end, we keep a running sum.
  • If the multiplier bit is zero, add the (shifted) multiplicand to the running sum.
  • If the bit is zero, simply skip the addition.

This results in the following algorithm

    product ← 0
    for i = 0 to 31
        if LOB of multiplier = 1
            product = product + multiplicand
        shift multiplicand left 1 bit
        shift multiplier right 1 bit
  

Do on the board 4-bit multiplication (8-bit registers) 1100 x 1101. Since the result has (up to) 8 bits, this is often called a 4x4→8 multiply.

The First Attempt

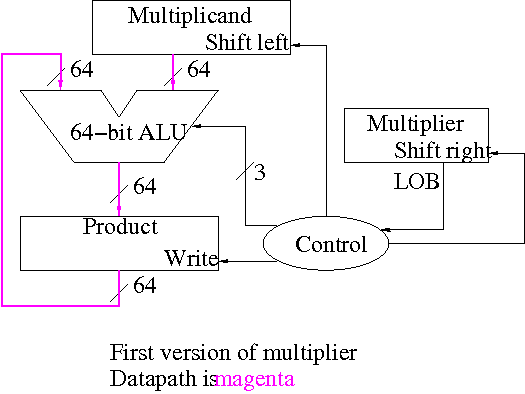
The diagrams below are for a 32x32-->64 multiplier.

What about the control?

• Always give the ALU the ADD operation
• Always send a 1 to the multiplicand to shift left
• Always send a 1 to the multiplier to shift right
• Pretty boring so far but
  • Send a 1 to write line in product if and only if LOB multiplier is a 1
  • I.e. send LOB to write line
  • I.e. it really is pretty boring

This works!

But, when compared to the better solutions to come, is wasteful of resourses and hence is

• slower
• hotter
• bigger
• all these are bad

An Improved Circuit

The product register must be 64 bits since the product can contain 64 bits.

Why is multiplicand register 64 bits?

• So that we can shift it left
• I.e., for our convenience.
  By this I mean it is not required by the problem specification,
  but only by the solution method chosen.

Why is ALU 64-bits?

• Because the product is 64 bits
• But we are only adding a 32-bit quantity to the product at any one step.
• Hmmm.
• Maybe we can just pull out the correct bits from the product.
• Would be tricky to pull out bits in the middle because which bits to pull changes each step

POOF!! ... as the smoke clears we see an idea.

We can solve both problems at once

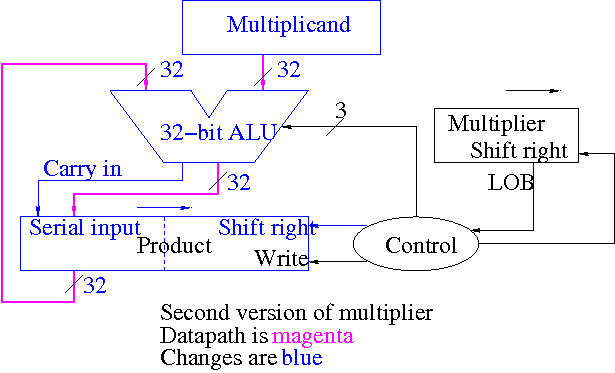
• DON'T shift the multiplicand left
  • Hence register is 32-bits.
  • Also register need not be a shifter
  
  
• Instead shift the product right!
  
  
• Add the high-order (HO) 32-bits of product register to the multiplicand and place the result back into HO 32-bits
  • Only do this if the current multiplier bit is one.
    
    
  • Use the Carry Out of the sum as the new bit to shift in
    
    
  • The book forgot the last point but their example used numbers too small to generate a carry

This results in the following algorithm

    product <- 0
    for i = 0 to 31
        if LOB of multiplier = 1
            (serial_in, product[32-63]) <- product[32-63] + multiplicand
        shift product right 1 bit
        shift multiplier right 1 bit
  

What about control

• Just as boring as before
• Send (ADD, 1, 1) to (ALU, multiplier (shift right), Product (shift right)).
• Send LOB to Product (write).

Redo same example on board

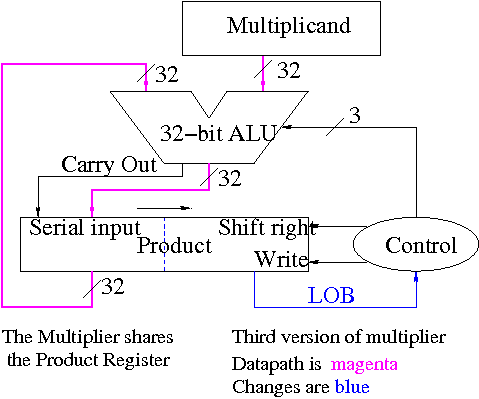
A final trick (gate bumming, like code bumming of 60s)

• There is a waste of registers, i.e. not full unilization.
  • The multiplicand is fully unilized since we always need all 32 bits.
  • But once we use a multiplier bit, we can toss it so we need less and less of the multiplier as we go along.
  • And the product is half unused at beginning and only slowly ...
  • POOF!!
  
  
• Timeshare the LO half of the product register.
  • In the beginning LO half contains the multiplier.
  • Each step we shift right and more goes to product less to multiplier.
  
  

The algorithm changes to:

    product[0-31] <- multiplier
    for i = 0 to 31
      if LOB of product = 1
        (serial_in, product[32-63]) <- product[32-63] + multiplicand
      shift product right 1 bit
  

Control again boring.

• Send (ADD, 1) to (ALU, Product (shift right)).
• Send LOB to Product (write).

Redo the same example on the board.

Signed Multiplication

The above was for unsigned 32-bit multiplication. What about signed multiplication?

• Save the signs of the multiplier and multiplicand.
• Convert multiplier and multiplicand to non-neg numbers.
• Use above algorithm.
• Only use 31 steps not 32 since there are only 31 multiplier bits (the HOB of the multiplier is the sign bit, not a bit used for multiplying).
• Compliment product if original signs were different.

There are faster multipliers, but we are not covering them.

3.5: Division

We are skiping division.

3.6: Floating Point

We are skiping floating point.

3.7: Real Stuff: Floating Point in the IA-32

We are skiping floating point.

Homework: Read for your pleasure (not on exams) 3.8 Fallacies and Pitfalls, 3.9 Conclusion, and 3.10 ``Historical Perspective'' (the last is on the CD).