Computer Architecture

Start Lecture #7

Shifters

MIPS (and most other) processors must execute shift (and rotate) instructions.

We could easily extend the ALU to do 1-bit shift/rotates (i.e., shift/rotate a 32-bit quantity by 1 bit), and then perform an n-bit shift/rotate as n 1-bit shift/rotates.

This is not done in practice. Instead a separate structure, called a barrel shifter is built outside the ALU.

Sequential Circuits, Memory, and State

Why do we need state?

• Memory (i.e., ram not just rom or prom).
• Counters.
• Reducing gate count.
  • Multiplying two n-bit numbers would require about n² gates if done with just combinatorial logic (think about how you multiply n-digit numbers.)
  • With sequential logic (state), multiplication can be done with about n gates.
    • What follows is unofficial (i.e. too fast to understand).
    • Shift register holds partial sum.
    • Real slick is to share this shift reg with multiplier.
    • We will do this circuit later in the course.

B.7: Clocks

Assume you have a physical OR gate. Assume the two inputs are both zero for an hour. At time t one input becomes 1. The output will OSCILLATE for a while before settling on exactly 1. We want to be sure we don't look at the answer before its ready.

This will require us to establish a clocking methodology, i.e. an approach to determining when data is valid.

First, however, we need some ...

Terminology

Micro-, Mega-, and Friends

Frequency and period

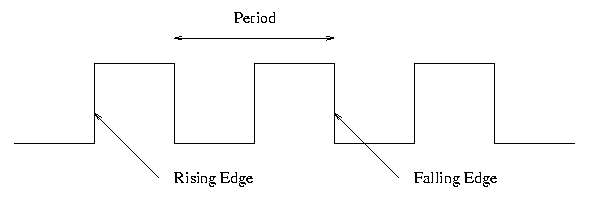
Consider the idealized waveform shown on the right. The horizontal axis is time and the vertical axis is (say) voltage.

If the waveform repeats itself indefinitely (as the one on the right does), it is called periodic.

The time required for one complete cycle, i.e., the time between two equivalent points in consecutive cycles, is called the period.

Since it is a time, period is measured in units such as seconds, days, nanoseconds, etc.

The rate at which cycles occur is called the frequency.

Since it is a rate at which cycles occur, frequency is measured in units such as cycles per hour, cycles per second, kilocycles per microweek, etc.

The modern (and less informative) name for cycles per second is Hertz, which is abbreviated Hz.

Prediction: At least one student will confuse frequency and periods on the midterm or final and hence mess up a gift question. Please, prove me wrong!

Make absolutely sure you understand why

1. A kilohertz clock is (a million times) faster than a millihertz clock.
2. A clock with a kilosecond period is (a million times) slower than one with a millisecond period.

Edges

Look at the diagram above and note the rising edge and the falling edge.

We will use edge-triggered logic, which means that state changes (i.e., writes to memory) occur at a clock edge.

For each design we choose to either

• Have all state changes occur at rising edges or
• Have all state changes occur at falling edges.

The edge on which changes occur (either the rising or falling edge) is called the active edge. For us, choosing which edge is active is basically a coin flip.

Synchronous system

Now we are going to add state elements to the combinational circuits we have been using previously.

Remember that a combinational/combinatorial circuits has its outpus determined solely by its input, i.e. combinatorial circuits do not contain state.

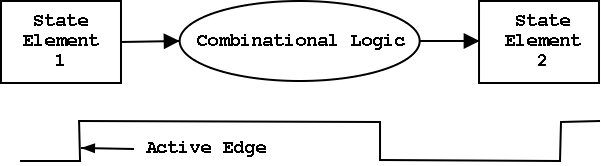
State elements include state (naturally).

• That is state elements are memory.
• State elements have clock as an input.
• These elements change state only at the active edge of the clock.
• They Always produce output, which is based on the current state.
• All signals that are written to state elements must be valid at the time of the active edge.
• For example, if cycle time (of the clock) is 10ns, the designer must ensure that combinational circuit used to compute new state values completes in 10ns.
• So state elements change at the active edge, the combinatorial circuit stabilizes between active edges.

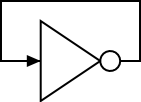
Combinatorial circuits can NOT contain loops. For example imagine an inverter with its output connected to its input. So if the input is false, the output becomes true. But this output is wired to the input, which is now true. Thus the output becomes false, which is the new input. So the output becomes true ... .
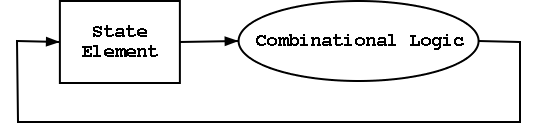However sequential circuits CAN and often Do contains loops.

• Think of state elements as registers or memory.
• Can have loops like at the right.
• For example imagine the assembler instruction
  add-register r1=r1+r1
  The state element is register number 1 and the combinatorial circuit is a full adder.

B.8: Memory Elements: Flip-Flops, Latches, and Registers

We will use only edge-triggered, clocked memory in our designs as they are the simplest memory to understand. So our current goal is to construct a 1-bit, edge-triggered, clocked memory cell. However, to get there we will proceed in three stages.

1. We first show how to build unclocked memory.
2. Then, using unclocked memory, we build level-sensitive clocked memory.
3. Finally from level-sensitive clocked memory we build edge-triggered clocked memory.

Unclocked Memory

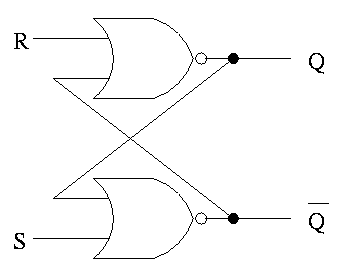
The only unclocked memory we will use is a so called S-R latch (S-R stands for Set-Reset).

When we define latch below to be a level-sensitive, clocked memory, we will see that the S-R latch is not really a latch.

The circuit for an S-R latch is on the right. Note the following properties.

• The S-R latch is constructed from Cross-coupled nor gates.
• Consider the four possible inputs.
• We do NOT assert both S and R at the same time (the output is not defined in this case).
• When S is asserted (i.e., S=1 and R=0):
  • The latch is Set (that's why it is called S).
  • Q becomes true (Q is the output of the latch).
  • Q' becomes false (Q' is the complemented output).
• When R is asserted:
  • The latch is Reset.
  • Q becomes false.
  • Q' becomes true.
• When neither one is asserted:
  • The latch retains its value, i.e. Q and Q' stay as they were.
  • This last statement is the memory aspect.

Clocked Memory: Flip-flops and latches

The S-R latch defined above is UNclocked memory; unfortunately the terminology is not perfect.

For both flip-flops and latches the output equals the value stored in the structure. Both have an input and an output (and the complemented output) and a clock input as well. The clock determines when the internal value is set to the current input. For a latch, the output can change whenever the clock is asserted (level sensitive). For a flip-flop, changes occur only at the active edge.

D latch

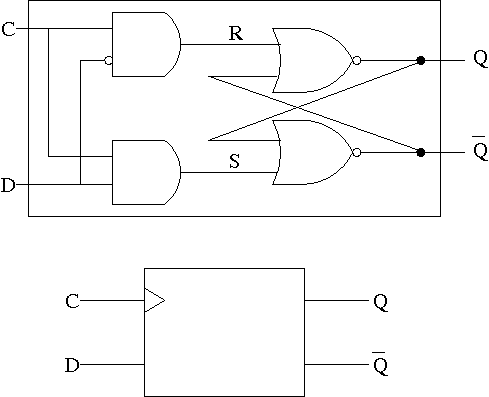
The D stands for data.

Note the following properties of the D latch circuit shown on the right.

• The left part of the circuit uses the clock; the right part is essentially a D latch.
• When the clock is low, both R and S are forced low so the outputs (Q and Q') don't change.
• When the clock is high, S=D and R=D' so the value stored is D and Q, the output of the latch, is D.
• The output changes when input changes and the clock is asserted, that is the latch is Level sensitive rather than edge triggered.

A D latch is sometimes called a transparent latch since, whenever the clock is high, the output equals the input (the input passes right through the latch).

We won't use D latches in our designs, except right now to our workhorse, the master-slave flip-flop, an edge-triggered memory cell.

The lower diagram is how a D-latch is normally drawn.



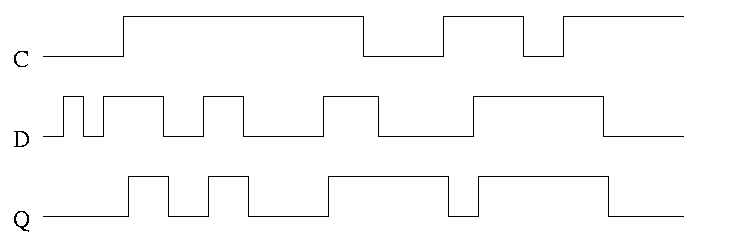
In the traces to the right notice how the output follows the input when the clock is high and remains constant when the clock is low. We assume the stored value was initially low.

D or Master-Slave Flip-flop

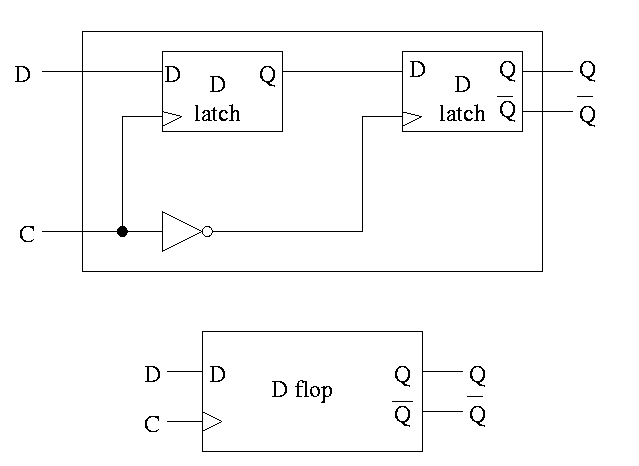
This structure was our goal. It is an edge-triggered, clocked memory.

The circuit for a D flop is on the right has the following properties.

• The D flop is built from D latches, which are transparent.
• The flop however is Not transparent
  • Changes to the output occur only at the active edge.
  • The circuit in the diagram has the falling edge as active edge.
• Sometimes called a master-slave flip-flop, the left latch is the master and the right the slave.
• The substructures reuse the same letters as the main structure but have different meaning (similar to block structured languages in the algol style).
• The master latch is set during the time the clock is asserted. Remember that the latch is transparent, i.e. it follows its input when its clock is asserted. But the second latch is ignoring its input at this time. When the clock falls, the 2nd latch pays attention and the first latch keeps producing whatever D was at fall-time.
• Actually D must remain constant for some time around the active edge.
  • The set-up time before the edge.
  • The hold time after the edge.
  • See the discussion and diagram below.

Homework: Move the inverter to the other latch. What has changed?

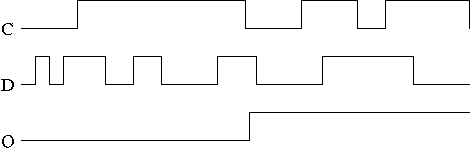The picture on the right is for a master-slave flip-flop. Note how much less wiggly the output is in this picture than before with the transparent latch. As before we are assuming the output is initially low.

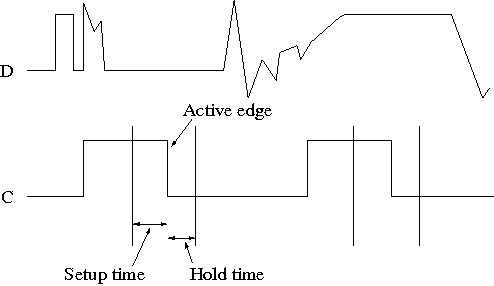This picture shows the setup and hold times discussed above.

• It is crucial when building circuits with flip flops that D is stable during the interval around the active edge including the setup and hold times.
• Note that D is wild outside the critical interval, but that is OK.
• We will not be emphasizing setup and hold requirements in this course.

Homework: Which code better describes a flip-flop and which a latch?

    repeat {
       while (clock is low) {do nothing}
       Q=D
       while (clock is high) {do nothing}
    } until forever

  or

    repeat {
    while (clock is high) {Q=D}
    } until forever