Computer Architecture

Start Lecture #5

Remark: Lab 3 assigned.

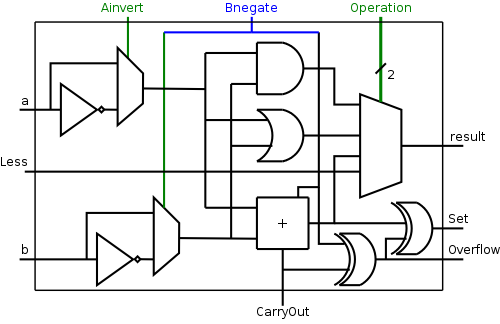
A Simple Observation

The CarryIn to the LOB and Binvert to all the 1-bit ALUs are always the same. So the ALU has just one input called Bnegate, which is sent to the appropriate inputs in the 1-bit ALUs. The final 1-bit cell of the ALU is shown on the right.

Note that the circuit is the same for all bits; however different bits are wired differently, i.e., they have different inputs and their outputs are sent to different places.

Equality Detection

To see if A = B we simply form A-B and test if the result is zero

• To see if all the bits are zero, is just a large NOR.
• This is conceptually trivially, but does require some wiring.

The Final Result

The final 32-bit ALU is shown below on the left. Again note that all the bits have the same circuit. The lob and hob have special external wiring; the other 30 bits are wired the same.

To the right of this diagram we see the symbol used for an ALU.

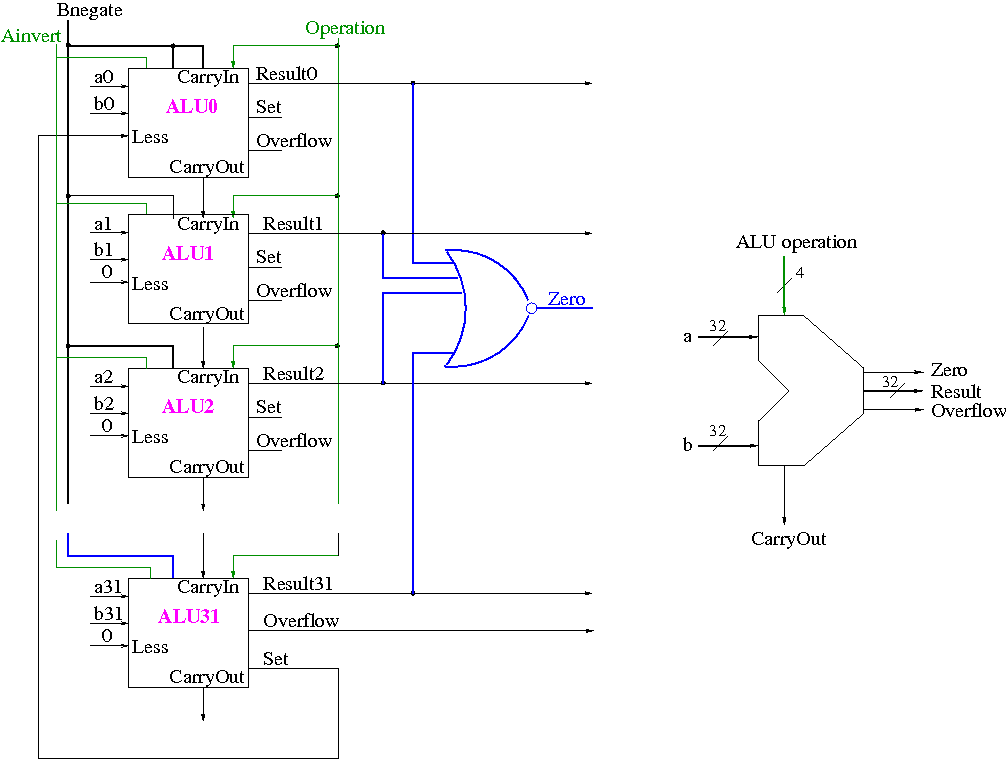
What are the control lines?

• Ainvert (1 bit)
• Bnegate (1 bit)
• OP (2 bits)

What functions can we perform?

function	4-bit cntl	Ainv	Bneg	Oper
AND	0000	0	0	00
OR	0001	0	0	01
ADD	0010	0	0	10
SUB	0110	0	1	10
slt	0111	0	1	11
NOR	1100	1	1	00

• AND
• OR
• ADD
• SUB
• NOR
• slt (set on less than)

We think of the three control lines Ainvert, Bnegate, and Operation as forming a single 4-bit control line. The table on the right shows what four bit value is needed for each function.

Defining the MIPS ALU in Verilog

Skipped.

B.6: Faster Addition: Carry Lookahead

This adder is much faster than the ripple adder we did before, especially for wide (i.e., many bit) addition.

Fast Carry Using Infinite Hardware

This is a simple (theoretical) result.

1. An adder is a combinatorial circuit hence it can be constructed with two (or three if you count the bubbles) levels of logic. Done


2. Consider 32-bit (or 64-bit, or 128-bit, or N-bit) addition, R=A+B.
   • This is a logic function with 32+32+1=65 binary inputs (A, B, and the CarryIn to the lob).
   • It has 33 outputs R and the final CarryOut.
   • Hence it can be expressed by a truth table having 2⁶⁵ rows and 65+33=98 columns.
   • This is a gigantic truth table (about 3 billion trillion entries), but nonetheless finite.
   • The corresponding PLA needs no more than 2⁶⁵ minterms feeding no more than 33 ORs.
   • Since each minterm is just an AND (with some bubbles) it is just one level of logic (or two if you count the bubbles). The ORs are just one level of logic, so we get a total of two (or three).
   • You could object that each minterm is the AND of a bunch (2N+1, for N-bit addition) of inputs so perhaps shouldn't be thought of as a single level of logic (even ignoring the bubbles).
   • The same consideration applies to the ORs, which might have even more (2^2N+1) inputs.
   • The above is a worst case analysis. The actual circuit for addition is probably not quite as bad, but still completely impractical for real 32-bit adders
   
   
3. The above applied to any logic function; here are the calculations specific for addition.
   • Each of the 1-bit adders we built were fast (just a few gate delays); the trouble was that the CarryIn to the upper order bits took a long time to calculate. We can calculate all the CarryIn's from the inputs a, b, and CarryIn₀ using two levels of logic.
   • We use c0 for CarryIn₀, c1 for CarryIn₁, c2 for CarryIn₂, etc.
   • c0 is an input.
   • c1 = a0 b0 + a0 c0 + b0 c0
   • c2 = a1 b1 + a1 c1 + b1 c1
           = a1 b1 + a1 a0 b0 + a1 a0 c0 + a1 b0 c0 + b1 a0 b0 + b1 a0 c0 + b1 b0 c0
   • c3 = a2 b2 + a2 c2 + b2 c2 = ... (substitute for c2)
   • etc.

Fast Carry Using the First Level of Abstraction: Propagate and Generate

At each bit position we have two input bits a and b as well as a CarryIn input. We now define two other bits propagate and generate (p=a_i+b_i and g=a_ib_i).

• We can calculate p and g quickly (one gate delay).
• It is crucial to note that p and g depend only on a and b.
• Specifically p and g do NOT depend on the CarryIn.
• Hence p and g for all bits can be calculated at once, there is no ripple effect.
• The idea behind propagate is that p is true if the current bit will propagate a carry from its input to its output.
• The idea behind generate is that g is true if the current bit will generate a carry out (independent of the carry in).
• It is easy to see that p = (a OR b), i.e.

  	if and only if (a OR b) {
  	  if there is a carry in
            then there is a carry out
  	}
        

• It is easy to see that g = (a AND b), i.e.

  	if and only if (a AND b)
  	then there will be a carry-out independent of the carry-in
        

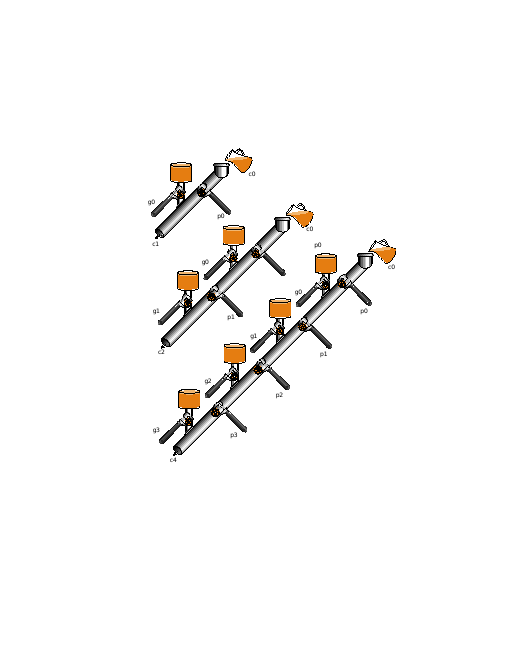
To summarize, using a subscript i to represent the bit number,

    to generate  a carry:   gi = ai bi
    to propagate a carry:   pi = ai+bi
  

The diagram on the right, from P&H, gives a plumbing analogue for generate and propagate. A full size version of the diagram is here in pdf.

The point is that liquid enters the main pipe if either the initial CarryIn or one of the generates is true. The water exits the pipe at the lower left (i.e., there is a CarryOut for this bit position) if all the propagate valves are open from the lowest liquid entrance to the exit.

The two diagrams in these notes are from the 2e; the colors changed between editions.

Given the generates and propagates, we can calculate all the carries for a 4-bit addition (recall that c0=C_in is an input) as follows (this is the formula version of the plumbing):

    c1 = g0 + p0 c0
    c2 = g1 + p1 c1 = g1 + p1 g0 + p1 p0 c0
    c3 = g2 + p2 c2 = g2 + p2 g1 + p2 p1 g0 + p2 p1 p0 c0
    c4 = g3 + p3 c3 = g3 + p3 g2 + p3 p2 g1 + p3 p2 p1 g0 + p3 p2 p1 p0 c0
  

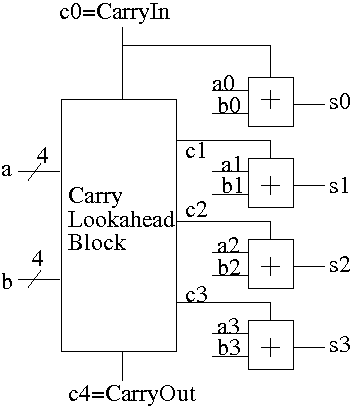
Thus we can calculate c1 ... c4 in just two additional gate delays given the p's and g's (where we assume one gate can accept upto 5 inputs). Since we get gi and pi after one gate delay, the total delay for calculating all the carries is 3 (this includes c4=Carry-Out)

Each bit of the sum si can be calculated in 2 gate delays given ai, bi, and ci. Thus, for 4-bit addition, 5 gate delays after we are given a, b and Carry-In, we have calculated s and Carry-Out.

We show this in the diagram on the right.

• The Carry Lookahead Block has inputs a, and b and the carry-in. The block calculates the p's and g's internally (not shown in the diagram) and then calculates the carries, which are the outputs of the block. The block requires 3 gate delays.
• Each small box labeled + is the part of a full adder that calculates the sum
          s = ai + bi + ci.
  Note that the carry-out is not calculated by this box. The box requires 2 gate delays.
• Note the division of labor: One block calculates the p's, g's, and carries; other logic calculates the sum.

Thus, for 4-bit addition, 5 gate delays after we are given a, b and Carry-In, we have calculated s and Carry-Out using a modest amount of realistic (no more than 5-input) logic.

How does the speed of this carry-lookahead adder CLA compare to our original ripple-carry adder?

• We have just seen that a 4-bit CLA completes its calculation in 5 gate delays.
• The ripple-carry adder is composed of 1-bit full adders (FAs).
• Each FA needs only two gate delays. Our design used more, but we were aiming for clarity not speed. It is a combinatorial circuit so of course theoretically it can be done in 2 gate delays (assuming the bubbles are free) and the design you get in this way is practical as well.
• But the calculation of bit i takes two gate delays starting from when the calculation of the previous bit is finished since bit i needs the CarryOut of bit i-1 as its own CarryIn.
• Thus the time required for a 4-bit adder is 4*2=8 gate delays.

Fast Carry Using the Second Level of Abstraction

We have finished the design of a 4-bit CLA; the next goal is a 16-bit fast adder. Let's consider, at varying levels of detail, five possibilities.

1. Ripple carry. Simple, we know it, but not fast.
2. General 2 levels of logic. Always applicable, we know it, but not practical.
3. Extend the above design to 16 bits. Possible, we could do it, but some gates have 17 inputs. Would need a tree to reduce the input count.
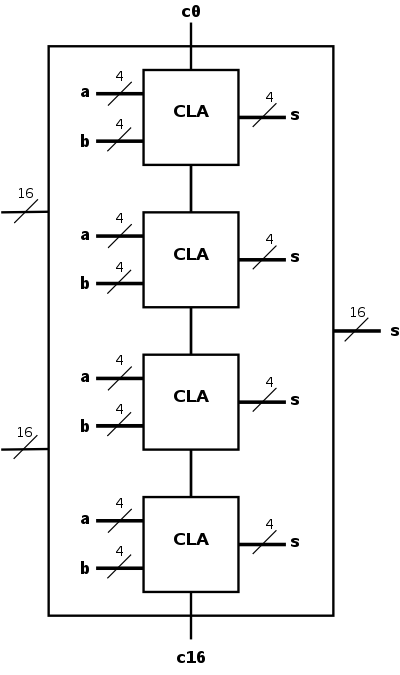
4. Put together four of the 4-bit CLAs. Shown in the diagram to the right is a schematic of our 4-bit CLA and a 16-bit adder constructed from four of them.
   • As black boxes, both ripple-carry adders and carry-lookahead adders (CLAs) look the same.
   • We could simply put four CLAs together and let the Carry-Out from one be the Carry-In of the next. That is, we could put these CLAs together in a ripple-carry manner to get a hybrid 16-bit adder.
   • Since the Carry-Out is calculated in 3 gate delays, the Carry-In to the high order 4-bit adder is calculated in 3*3=9 delays.
   • Hence the overall Carry-Out takes time 9+3=12 and the high order four bits of the sum take 9+5=14. The other bits take less time.
   • So this mixed 16-bit adder takes 14 gate delays compared with 2*16=32 for a straight ripple-carry 16-bit adder.
   • Note that this hybrid structure is not a true 16-bit CLA because the 4-bit structures are ripple-carry connected.
5. Be more clever and put together the 4-bit CLAs in a carry-lookahead manner. One could call the result a 2-level CLA.
   • We have 33 inputs a0,...,a15; b0,...b15; c0=Carry-In
   • We want 17 outputs s0,...,s15; c16=c=Carry-Out
   • Again we are assuming a gate can accept upto 5 inputs.
   • It is important that the number of inputs per gate does not grow with the number of bits we are adding.
   • If the technology available supplies only 4-input gates (instead of the 5-input gates we are assuming), we would use groups of three bits rather than four.
   • This will take us some time to develop and is our next goal.