Computer Architecture

Start Lecture #4

Remark: Show in class how to broadcast S (select line) to many ANDs (used for wide muxes in 2nd lab) and assign lab 2.

Full Adder

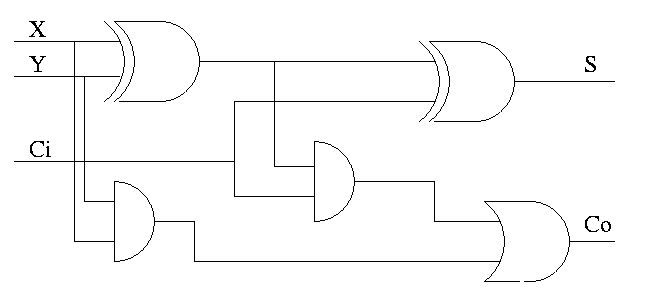
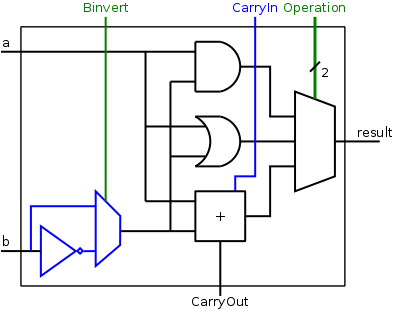
Now we include the carry-in.

• Three 1-bit inputs: X, Y and Ci.
• Two 1-bit output: S and Co.
• S = the total number of 1s in X, Y, and Ci is odd
• Co = #1s is at least 2.
• The diagram on the right uses logic formulas for S and Co equivalent to the definitions given above (see homework just below).

Homework:

• Draw truth table (8 rows)
• Show S = X ⊕ Y ⊕ Ci
• Show Co = XY + (X ⊕ Y)Ci

Combining 1-bit AND, OR, and ADD

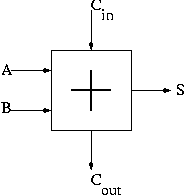
We have implemented 1-bit versions of AND (a basic gate), OR (a basic gate), and SUM (the FA just constructed, which we henceforth draw as shown on the right). We now want a single structure that, given another input (the desired operation, another one of those control lines), produces as output the specified operation.

There is a general principle used to produce a structure that yields either X or Y depending on the value of operation.

1. Implement a structure that always computes X.
2. Implement another structure that always computes Y.
3. Mux X and Y together using operation as the select line.

This mux, with an operation select line, gives a structure that sometimes produces one result and sometimes produces another. Internally both results are always produced.

In our case we have three possible operations so we need a three way mux and the select line is a 2-bit wide bus. With a 2-bit select line we can specify 4 operations, for now we are using only three.

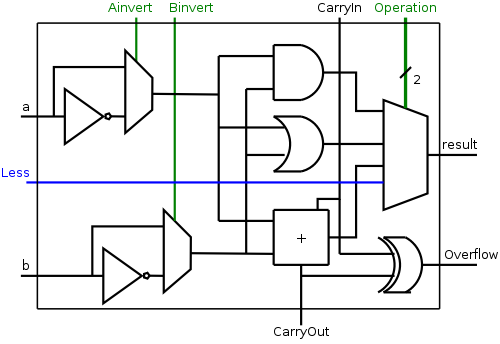
We show the diagram for this 1-bit ALU on the right.

The Operation input is shown in green to distinguish it as a control line rather than a data line. That is, the goal is to produce two bits of result from 2 (AND, OR) or 3 (ADD) bits of data. The 2 bits of control tell what to do, rather than what data to do it on.

The extra data output (CarryOut) is always produced. Presumably if the operation was AND or OR, CarryOut is not used.

I believe the distinction between data and control will become quite clear as we encounter more examples. However, I wouldn't want to be challenged to give a (mathematically precise) definition.

A 32-bit ALU

A 1-bit ALU is interesting, but we need a 32-bit ALU to implement the MIPS 32-bit operations, acting on 32-bit data values.

For AND and OR, there is almost nothing to do; a 32-bit AND is just 32 1-bit ANDs so we can simply use an array of logic elements.

However, ADD is a little more interesting since the bits are not quite independent: The CarryOut of one bit becomes the CarryIn of the next.

A 32-bit Adder

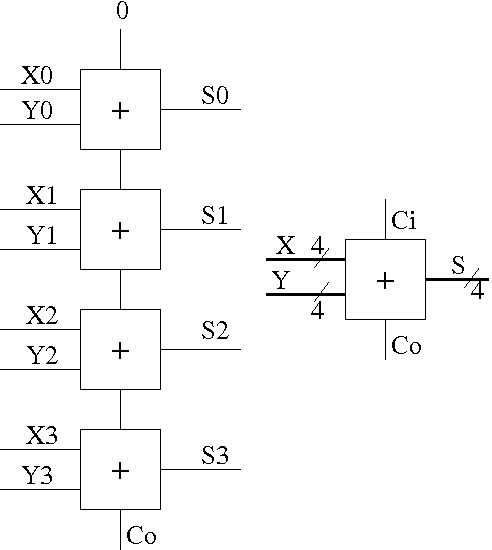
Let's start with a 4-bit adder.

• In the diagram to the near right, each box is a 1-bit full adder as above.
• The top FA is the low order bit (lob); the bottom FA is the hob.
• Note that the Carry-out of one 1-bit FA becomes the Carry-in of the next higher order 1-Bit FA.
• Note also that you do the same thing when you add numbers.
• Further to the right we show the 4-bit adder without showing the individual FAs.
• In this rightmost picture we have two 4-bit inputs (the addends), one 1-bit input (the Carry-in), one 4-bit output (the sum), and 1-bit output (the Carry-out).
• If all you ever wanted from the rightmost circuit was 4-bit addition, you would not have a Ci. Instead you would feed zero into the Ci of the lob as I did in the left picture.
• But you can put two of these 4-bit adders together to get an 8-bit adder. Simply connect the Co of one to the Ci of the second.

How about a 32-bit adder, or even an an n-bit adder ?

• No problem; just use n 1-bit FAs.
• Linear (time) complexity, i.e. the time for a 64-bit add is twice that for a 32-bit add, which itself is twice the time for a 16-bit add.
• This adder design is called ripple carry since the carry ripples down the circuit from the low order bit to the high order bit. The necessity for the carry to ripple down the circuit one bit at a time is why the circuit has linear complexity.
• Faster (logarithmic complexity) methods exist. Indeed we will learn one soon.

Combining 32-bit AND, OR, and ADD

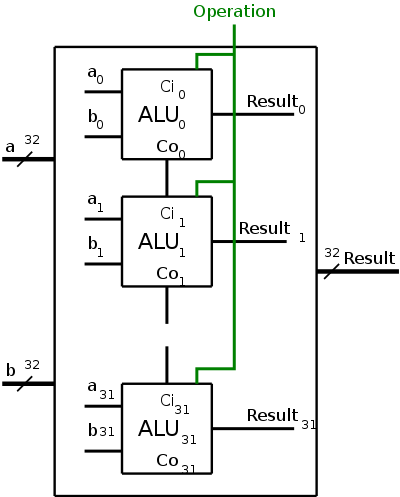
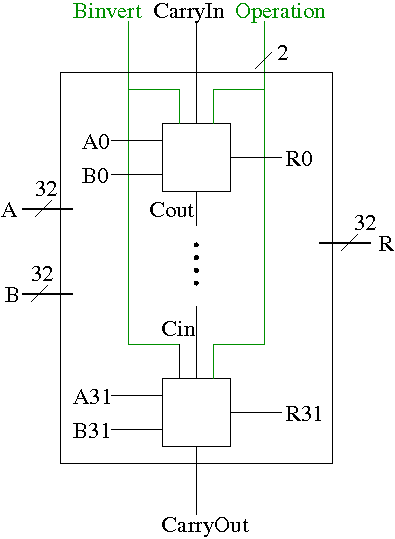
To obtain a 32-bit ALU, we put together the 1-bit ALUs in a manner similar to the way we constructed a 32-bit adder from 32 FAs. Specifically we proceed as follows and as shown in the figure on the right.

1. Use an array of logic elements for the logic. The individual logic element is the 1-bit ALU.
2. Use buses for A, B, and Result.
3. Broadcast Operation to all of the internal 1-bit ALUs. This means wire the external Operation to the Operation input of each of the internal 1-bit ALUs.

Facts Concerning (4-bit) Two's Complement Arithmetic

Remark
This is one place were the our treatment must go a little out of order. Appendix B in the book assumes you have read the chapter on computer arithmetic; in particular it assumes that you know about two's complement arithmetic.

I do not assume you know this material and we will cover it later, when we do that chapter. What I will do here is assert some facts about two's complement arithmetic that we will use to implement the circuit for SUB.
End of Remark.

For simplicity I will be presenting 4-bit arithmetic. We are really interested in 32-bit arithmetic, but the idea is the same and the 4-bit examples are much shorter (and hence less likely to contain typos).

4-bit Twos's Complement Numbers

With 4 bits, there can be only 16 numbers. One of them is zero, 8 are negative, and 7 are positive.

The high order bit (hob) on the left is the sign bit. The sign bit is zero for positive numbers and for the number zero; the sign bit is one for negative numbers.

Zero is written simply 0000.

1-7 are written 0001, 0010, 0011, 0100, 0101, 0110, 0111. That is, you set the sign bit zero and write 1-7 using the remaining three lob's. This last statement is also true for zero.

-1, -2, ..., -7 are written by taking the two's complement of the corresponding positive number. The two's complement is computed in two steps.

1. Take the (ordinary) complement, i.e. turn ones to zeros and vice versa. This is sometimes called the one's complement.
   For example, the (4-bit) one's complement of 3 is 1100.
2. Add 1.
   For example, the (4-bit) two's complement of 3 is 1101.

If you take the two's complement of -1, -2, ..., -7, you get back the corresponding positive number. Try it.

If you take the two's complement of zero you get zero. Try it.

What about the 8th negative number?
-8 is written 1000.
But if you take its (4-bit) two's complement, you must get the wrong number because the correct number (+8) cannot be expressed in 4-bit two's complement notation.

Two's Complement Addition and Subtraction

Amazingly easy (if you ignore overflows).

• Add: Just use a 4-bit adder, do NOT treat the sign bit in a special way, and discard the final carry-out.
• Sub: Take the two's complement of the subtrahend (the second number) and add as above.

Implementing SUB (with AND, OR, and ADD)

No change is needed to our circuit above to handle two's complement numbers for AND/OR/ADD. That statement is not clear for ADD and will be shown true later in the course.

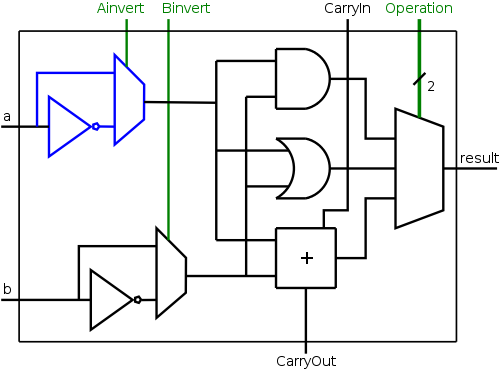
We wish to augment the ALU so that we can perform subtraction as well. As we stated above, A-B is obtained by taking the two's complement of B and adding. A 1-bit implementation is drawn on the right with the new structures in blue (I often use blue for this purpose). The enhancement consists of

1. Using an inverter to get the one's complement of B.
2. Using a mux with control line (in green) Binvert to select whether B or B' is fed to the adder.
3. Using a clever trick to obtain the effect of B's two complement when we are using B's one complement. Namely we set Cin, the carry-in to the lob, equal to 1 instead of 0. This trick increases the sum by one and, as a result, calculates A+B'+1, which is A plus the two's complement of B, which is A-B.
4. So for the lob CarryIn is kinda-sorta a data line used as a control line.
5. As before, setting Operation to 00 and 01 gives AND and OR respectively, providing we de-assert Binvert. CarryIn is a don't care for AND and OR.
6. To implement addition we use opcode 10 as before and de-assert both Binvert and CarryIn
7. To implement subtraction we again use opcode 10 but we assert both Binvert and CarryIn

Extending to 32 Bits

A 32-bit version is simply a bunch of the 1-bit structures wired together as shown on the right.

• The Binvert and Operation control lines are broadcast to all of the 1-bit ALUs.
• As before Operation is 00 for AND, 01 for OR, and 10 for both ADD and SUB.
• For AND and OR de-assert BInvert. CarryIn is a don't care.
• For addition de-assert both Binvert and CarryIn.
• For subtraction assert both Binvert and CarryIn.
• We could implement other functions as well. For example, we get AB' by asserting Binvert and setting Operation=00. That one is not so useful, but a variant is useful and we will implement it soon.

Tailoring the 32-bit ALU to MIPS

AND, OR, AND, and SUB are found in nearly all ALUs. In that sense, the construction up to this point has been generic. However, most real architectures have some extras. For MIPS they include.

1. NOR, not very special and very easy.
2. Overflow handling, common but not so easy.
3. Set on less than (slt), not common and not so easy.
4. Equality test, not very special and easy.

Implementing NOR

We noted above that our ALU already gives us the ability to calculate AB', a fairly uncommon logic function. A MIPS ALU needs NOR and, by DeMorgan's law,
A NOR B = (A + B)' = A'B',
which is rather close, we just need to invert A as well as B.

The diagram on the right shows the needed structures: an inverter to get A', a mux to choose between A and A', and a control line for the mux.

NOR is obtained by asserting Ainvert and Binvert and setting Operation=00.

The other operations are done as before, with Ainvert de-asserted.

The 32-bit version is a straightforward ...

Homework: Draw the 32-bit ALU that supports AND, OR, ADD, SUB, and NOR.

Overflows

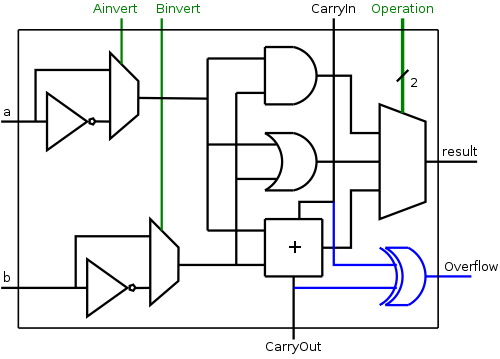
Remark: As with two's complement arithmetic, I just present the bare boned facts here; they are explained later in the course.

The facts are trivial (although the explanation is not). Indeed there is just one fact.

1. An overflow occurs for two's complement addition (which includes subtraction) if and only if the carry-in to the sign bit does not equal the carry out from the sign bit.

Only the hob portion of the ALU needs to be changed. We need to see if the carry-in is different from the carry-out, but that is exactly XOR. The simple modification to the hob structure is shown on the right.

Do on the board 4-bit twos complement addition of

1. 1 + 1
2. -1 + -1 Note that there is NO overflow despite a carry-out.
3. 6 + 6
4. -6 + -6

The 32-bit version is again a straightforward ...

Homework: Draw the 32-bit ALU that supports AND, OR, ADD, SUB, and NOR and that asserts an overflow line when appropriate.

Implementing Set on Less Than (SLT)

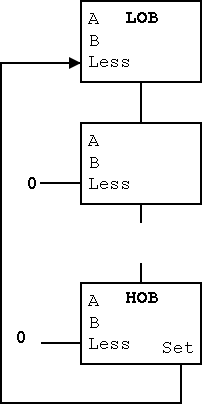
We are given two 32-bit, two's complement numbers A and B as input and seek a 32-bit result that is 1 if A<B and 0 otherwise. Note that only the lob of the result varies; the other bits are all 0.

The implementation is fairly clever as we shall see.

1. We need to set the LOB of the result equal to the sign bit of the subtraction A-B, and set the rest of the result bits to zero.


2. Idea #1. Give the 4-way mux another (i.e., fourth) input, called LESS. This input is brought in from outside the bit cell. To generate slt, we make the select line to the mux equal to 11 so that the the output is the this new input. See the diagram on the right.


3. For all the bits except the LOB, the LESS input is zero. This is trivial to do: Simply label a wire false or 0, or de-asserted and connected it to the 31 Less inputs (i.e., all but the LOB).


4. For the LOB we still need to figure out how to set less to the sign of A-B. Note that the circuit for the lob is the same as for the other bits; the difference is in the input to the circuit.


5. Recall that even though we have selected input 3 from the mux, all 4 inputs are computed. This is IMPORTANT: an OR gate always computes the OR of its inputs, whether you want it to or not, same for AND, etc.


6. Hence the adder is adding and if Binvert is asserted, Ainvert is de-asserted, and CarryIn is 1, the addition actually produces A-B.


7. Idea #2. Use the settings just mentioned so that the adder computes A-B (and the mux throws it away). Modify the HOB logic as follows (you could do this modification for all bits, but just use the result from the HOB).
   • Bring out the result of the adder (before the mux).
   • Take this new output from the HOB, call it SET and connect it to the Less input in idea #1 for the LOB.
   • Thus the Less for the LOB is correctly set and we are done!
   • The high level diagram of this maneuver is shown on the right.


8. Why didn't I show a detailed diagram for this method?
   Because this method is not used.


9. Why isn't the method used?
   Because it is wrong!

The problem with the above solution is that it ignores overflows. Consider the following 4-bit (instead of 32-bit) example.

• Try slt on -6 and +5.
• True subtraction gives -11.
• The negative sign in -11 indicates (correctly) that -6 < +5.
• But 4-bit subtraction gives a positive result (and asserts overflow).
• Hence the set output of the hob is zero and we send that to the Less input of the lob.
• Hence the circuit yields zero for slt given inputs -6 and +5, thereby claiming that -6 is not less than 5.

The fix is to use the correct rule for less than rather than the sometimes incorrect rule the sign bit of A-B is 1.

Homework: figure out correct rule, i.e. a non-pictorial version of problem B.24. Hint: When an overflow occurs, the sign bit is definitely wrong.

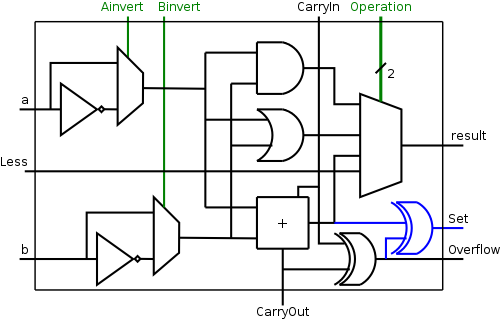
The diagram on the right shows the correct calculation of Set.