Computer Architecture

Start Lecture #3

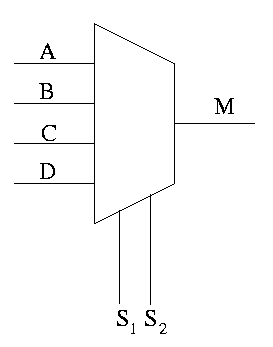
The diagram on the right shows a 4-input MUX.

Construct on the board an equivalent circuit with ANDs and ORs in three ways:

1. Construct the truth table (64 rows!) and write the sum of products form, one product (6-input AND) for each row and a gigantic 64-way OR. Just start this, don't finish it.
2. A simpler (more clever) two-level logic solution. Four ANDS (one per input), each gets one of the inputs and both select lines with appropriate bubbles. The four outputs go into a 4-way OR.
3. Construct a 2-input mux (using the clever solution). Then construct a 4-input mux using a tree of three 2-input muxes. One select line is used for the two muxes at the base of the tree, the other is used at the root.

All three of these methods generalize to a mux with 2^k input lines, and k select lines.

A 2-way mux is the hardware analogue of if-then-else.

    if S=0
        M=A
    else
        M=B
    endif

A 4-way mux is an if-then-elif-elif-else

    if S1=0 and S2=0
        M=A
    elif S1=0 and S2=1
        M=B
    elif S1=1 and S2=0
        M=C
    else -- S1=1 and S2=1
        M=D
    endif

Don't Cares (again)

S	I0	I1	O
0	0	X	0
0	1	X	1
1	X	0	0
1	X	1	1

Consider a 2-input mux. If the selector is 0, the output is I0 and the value of I1 is irrelevant. Thus, when the selector is 0, I1 is a don't care input. Similarly, when the selector is 1, I0 is a don't care input.

On the right we see the resulting truth table. Recall that without using don't cares the table would have 8 rows since there are three inputs; in this example the use of don't cares reduced the table size by a factor of 2.

The truth table for a 4-input mux has 64 rows, but the use of don't care inputs has a dramatic effect. When the selector is 01 (i.e, S0 is 0 and S1 is 1), the output equals the value of I1 and the other three I's are don't care. A corresponding result occurs for other values of the selector.

Homework: Draw the truth table for a 4-input mux making use of don't care inputs. What size reduction occurred with the don't cares?

Homework: B.13. (I am not sure what is meant by hierarchial; perhaps modular).
B.10. (Assume you have constant signals 1 and 0 as well.)

Recall that a don't care output occurs when for some input values (i.e., rows in the truth table), we don't care what the value is for certain outputs.

• Perhaps we know that this set of input values is impossible.
• Perhaps we know that we will mux out these outputs when we have the specified inputs.

Powers of 2 NOT Required

How can one construct a 5-way mux?

Construct an 8-way mux and use it as follows.

• Connect the five input signals to the first five inputs of the mux.
• Make sure the three select inputs never result in 5, 6, or 7.

Can do better by realizing the select lines equalling 5, 6, or 7 are don't cares and hence the 8-way can be customized and would use fewer gates than an 8-way mux.

PLAs—Programmable Logic Arrays (and PALs)

The idea is to partially automate the algorithmic way you can produce a circuit diagram (in the sums of product form) from a given truth table. Since the form of the circuit is always a bunch of ANDs feeding into a bunch of ORs, we can manufacture all the gates in advance of knowing the desired logic functions and when the functions are specified, we just need to make the necessary connections from the ANDs to the ORs. In essence all possible connections are configured but with switches that can be open or closed.

A	B	C	D	E	F
0	0	0	0	0	0
0	0	1	1	0	0
0	1	0	1	0	0
0	1	1	1	1	0
1	0	0	1	0	0
1	0	1	1	1	0
1	1	0	1	1	0
1	1	1	1	0	1

The description just given is more accurate for a PAL (Programmable Array Logic) than for a PLA, as we shall soon see.

Consider the truth table on the right, which we have seen before. It has three inputs A, B, and C, and three outputs D, E, F.

Below the truth table we see the corresponding logic diagram in sum of products form

Recall how we construct this diagram from the truth table.

• The circuit is in sum of products form.
• There is a big OR for each output. The OR has one input for each row that the output is true.
• Since there are 7 rows for which at least one output is true, there are 7 product terms that will be used in one or more of the ORs (in fact all seven will be used in D, but that is special to this example).
• Each of these product terms is called a Minterm.
• So we need seven ANDs, one for each minterm. Each AND takes a subset of A, B, C, A', B', and C' as inputs. In fact we can say more since some subsets (e.g., A and A') are never used. Instead of arbitrary subsets of the 6 inputs, we choose three inputs, either A or A', either B or B', and either C or C'. However, we will not make use of this refinement in the next diagram.
• This collection of ANDs is called the AND plane and the collection of ORs mentioned above is called the OR plane. The reason for calling them a plane will be clearer in the next diagram

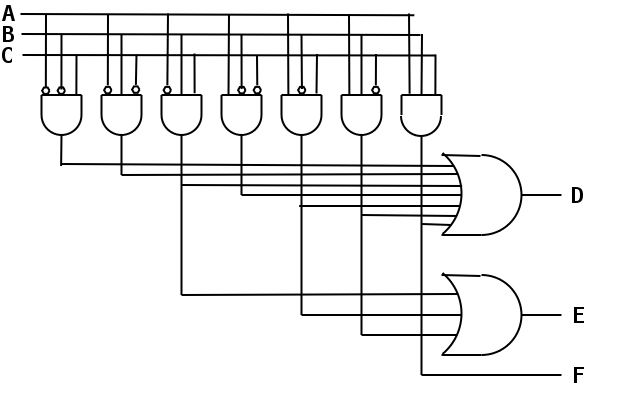
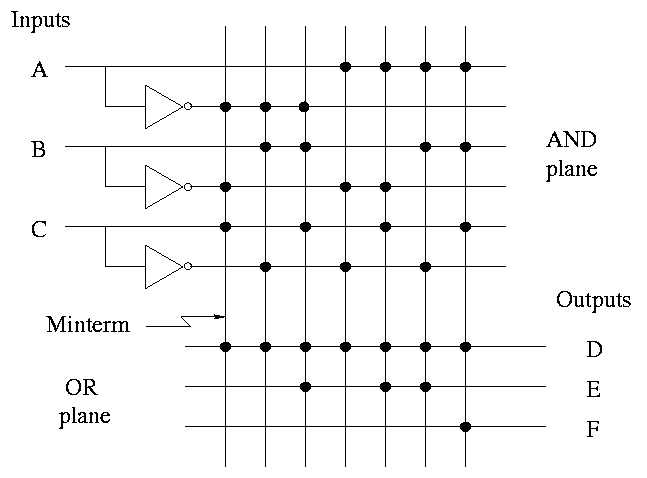
To the right, the above figure is redrawn in a more schematic style.

• This figure shows more clearly the AND plane, the OR plane, and the minterms.
• Rather than having bubbles (i.e., custom AND gates that invert certain inputs), we simply invert each input once and send the inverted signal all the way accross.
• AND gates are shown as vertical lines; ORs as horizontal.
• Note the dots used to represent connections.
• Imagine building a bunch of these but not yet specifying where the dots go. This would be a generic precursor to a PLA.

Finally, a PLA can be redrawn in the more abstract form shown on the right.

Before a PLA is manufactured all the connections are specified. That is, a PLA is specific for a given circuit. Hence the name Programmable Logic Array is somewhat of a misnomer since the device is not programmable by the user.

Homework: B.11 and B.12.

PAL (Programmable Array Logic)

A PAL can be thought of as a PLA in which the final dots are made by the user. The manufacturer produces a sea of gates. The user programs it to the desired logic function by adding the dots.

ROMs

One way to implement a mathematical function (or a java function without side effects) is to perform a table lookup.

A ROM (Read Only Memory) is the analogous way to implement a logic function.

• For a math function f we are given x and produce f(x).
• For a ROM with are given the address and produce the value stored at that address.
• Normally math functions are defined for an infinite number of values, for example f(x) = 3x for all real numbers x.
• We can't build an infinite ROM (sorry), so we are only interested in functions defined for a finite number of values. Today a billion is OK, but a trillion is not.
• How do we create a ROM for the function f(3)=4, f(6)=20 all other values don't care?
  Simply purchase a ROM with 4 in address 3 and 20 in address 6.
• Consider a function defined for all n-bit numbers (say n=20) and having a k-bit output for each input.
  • View an n-bit input as n 1-bit inputs.
  • View a k-bit output as k 1-bit outputs.
  • Since there are 2^n possible inputs and each requires a k 1-bit output, there are a total of (2^n)k bits of output, i.e. the ROM must hold (2^n)k bits.
  • Now consider a truth table with n inputs and k outputs. The total number of output bits is again (2^n)k (2^n rows and k output columns).
• Indeed the ROM implements a truth table, i.e. is a logic function.

Important: A ROM does not have state. It is another combinational circuit. That is, it does not represent memory. The reason is that once a ROM is manufactured, the output depends only on the input. I realize this sounds wrong, but it is right.

Indeed, we will shortly see that a ROM is like a PLA. Both are structures that can be used to implement a truth table.

The key property of combinational circuits is that the outputs depend only on the inputs. This property (having no state) is false for a RAM chip. The input to a RAM, just like the input to a ROM, is an address. The RAM responds by presenting at its outputs the value CURRENTLY stored at that address. Thus just knowing the input (i.e., the address) is not sufficient for determining the output.

A PROM is a programmable ROM. That is, you buy the ROM with nothing in its memory and then before it is placed in the circuit you load the memory, and never change it. This is like a CD-R.

An EPROM is an erasable PROM. It costs more but if you decide to change its memory this is possible (but is slow). This is like a CD-RW.

Normal EPROMs are erased by some ultraviolet light process. But EEPROMs (electrically erasable PROMS) are not as slow and are done electronically.

Flash is a modern EEPROM that is reasonably fast.

All these EPROMS are erasable not writable, i.e. you can't just change one byte to an arbitrary value. (Some modern flash rams can nearly replace true ram and perhaps should not be called EPROMS).

ROMs and PLAs

A ROM is similar to PLA

• Both can, in principle, implement any truth table.
• A 2Mx8 ROM can really implement any truth table with 21 inputs (2²¹=2M) and 8 outputs.
  • It stores 2M bytes.
  • In ROM-speak, it has 21 address pins and 8 data pins.
• A PLA with 21 inputs and 8 outputs might need to have 2M minterms (AND gates).
  • The number of minterms depends on the truth table itself.
  • For normal truth tables with 21 inputs the number of minterms is much less than 2²¹.
  • The PLA is manufactured with the number of minterms needed.
• Compare a PAL with a PROM.
  • Both can, in principle, implement any truth table.
  • Both are user programmable.
  • A PROM with n inputs and k outputs can implement any truth table with n inputs and k outputs.
  • An n-input, k-output PAL that you buy does not have enough gates for all possibilities since most truth tables with n inputs and k outputs require far fewer than k2ⁿ gates.

Don't Cares (bigger example)

• Sometimes not all the input and output entries in a truth table are needed. We indicate this with an X and it can result in a smaller truth table.
• Input don't cares.
  • The output doesn't depend on all inputs, i.e. the output has the same value no matter what value this input has.
  • We saw this when we did muxes.
• Output don't cares
  • For some input values, either output is OK.
    • This input combination is impossible.
    • For this input combination, the given output is not used (perhaps it is muxed out downstream).

The top diagram on the right is the full truth table for the following example (from the book). Consider a logic function with three inputs A, B, and C, and three outputs D, E, and F.

• If A or C is true, then D is true (independent of B).
• If A or B is true, then E is true (independent of C).
• F is true if exactly one of the inputs is true, but we don't care about the value of F if both D and E are true

The full truth table has 7 minterms (rows with at least one nonzero output).

The middle truth table has the output don't cares included.

Truth Table with Input and Output Don't Cares

A	B	C	D	E	F
0	0	0	0	0	0
0	0	1	1	0	1
0	1	0	0	1	1
X	1	1	1	1	X
1	X	X	1	1	X

Now do the input don't cares

• B=C=1 ==> D=E=11 ==> F=X ==> A=X
• A=1 ==> D=E=11 ==> F=X ==> B=C=X

The resulting truth table is also shown on the right. Note how much smaller it is

These don't cares are important for logic minimization. Compare the number of gates needed for the full truth table and the reduced truth table. There are techniques for minimizing logic, but we will not cover them.

Arrays of Logic Elements

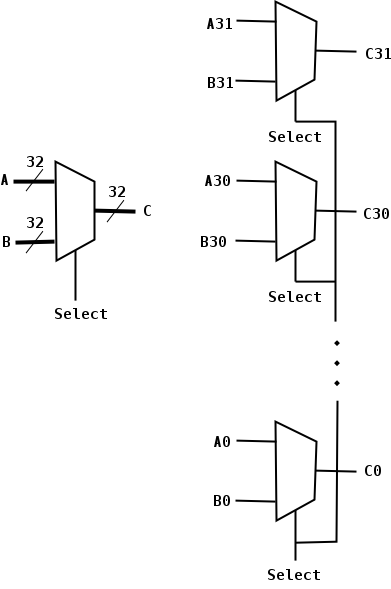
Often we want to consider signals that are wider than a single bit. An array of logic elements is used when each of the individual bits is treated similarly. As we will soon see, sometimes most of the bits are treated similarly, but there are a few exceptions. For example, a 32-bit structure might treat the lob (low order bit) and hob differently from the others. In such a case we would have an array 30 bits wide and two 1-bit structures.

• A Bus is a collection of (say n) data lines treated as a single logical (n-bit) value.
• We typically use an array of logic elements to process a bus. For example, the above mux switches between two 32-bit buses.
• We draw a bus using thicker lines and employ the by n notation.
• The diagram on the right shows a 32-bit, 2-way mux and an implementation using thirty-two 1-bit, 2-way muxes.

B.4: Using a Hardware Description Language

Skipped.

B.5: Constructing a Basic Arithmetic Logic Unit (ALU)

We will produce logic designs for the integer portion of the MIPS ALU (the floating point operations are more complicated and will not be implemented).

MIPS is a computer architecture widely used in embedded designs. In the 80s and early 90s, it was quite popular for desktop (or desk-side) computers. This was the era of the killer micros that decimated the market for minicomputers. (When I got my DECstation with a MIPS R3000, I think it was the fastest integer computer at NYU for a short while.)

Much of the design (all of the beginning part) is generic. I will point out when we are tailoring it for MIPS.

A 1-bit ALU

Our first goal will be a 1-bit wide structure that computes the AND, OR, and SUM of two 1-bit quantities. For the sum there is actually a third input, CarryIn, and a 2nd output, CarryOut.

Since out basic logic toolkit already includes AND and OR gates, our first real task is a 1-bit adder.

Half Adder

If the final goal was a 1-bit ALU, then we would not have a CarryIn. For a multi-bit ALU, the CarryIn for each bit is the CarryOut of the preceding lower-order bit (e.g., the CarryIn for bit 3 is the CarryOut from bit 2). When we don't have a CarryIn, the structure is sometimes called a half adder. Don't treat the name too seriously; it is not half of an adder.

• Two 1-bit inputs: X and Y.
• Two 1-bit outputs S (sum) and Co (carry out).
• No carry in.
• Draw truth table.

Homework: Draw the logic diagram.