Computer Architecture
V22.0436: Computer Architecture
2006-07 Fall
Allan Gottlieb
Mondays and Wednesdays 11:00-12:15
Room 102 Ciww
Start Lecture #1
Chapter 0: Administrivia
I start at Chapter 0 so that when we get to chapter 1, the
numbering will agree with the text.
0.1: Contact Information
- <my-last-name> AT nyu DOT edu (best method)
- http://cs.nyu.edu/~gottlieb
- 715 Broadway, Room 712
- 212 998 3344
0.2: Course Web Page
There is a web site for the course.
You can find it from my home page listed above.
- You can also find these lecture notes on the course home page.
Please let me know if you can't find it.
- The notes are updated as bugs are found or improvements made.
- I will also produce a separate page for each lecture after the
lecture is given.
These individual pages might not get updated as quickly as the
large page.
0.3: Textbook
The course text is Hennessy and Patterson,
Computer Organization and Design: The Hardware/Software Interface,
3rd edition.
- Available in the bookstore.
- The main body of the book assumes you know logic design.
- I do NOT make that assumption.
- We will start with appendix B, which is logic design review.
- Most of the figures in these notes are based on figures from the
course textbook.
The following copyright notice applies.
All figures from Computer Organization and Design:
The Hardware/Software Approach, Third Edition, by
David Patterson and John Hennessy, are copyrighted
material (COPYRIGHT 1998 MORGAN KAUFMANN
PUBLISHERS, INC. ALL RIGHTS RESERVED).
Figures may be reproduced only for classroom or
personal educational use in conjunction with the book
and only when the above copyright line is included. They
may not be otherwise reproduced, distributed, or
incorporated into other works without the prior written
consent of the publisher.
0.4: Computer Accounts and Mailman Mailing List
- You are entitled to a computer account, please get yours asap if
you don't already have one.
- Sign up for the course mailman mailing list
here.
- If you want to send mail just to me, use the address given
above, not not the mailing list.
- Questions on the labs should go to the mailing list.
You may answer questions posed on the list as well.
Note that replies are sent to the list.
- I will respond to all questions; if another student has answered the
question before I get to it, I will confirm if the answer given is
correct.
- Please use proper mailing list etiquette.
- Send plain text messages rather than (or at least in
addition to) html.
- Use the Reply command to contribute to the current thread,
but NOT to start another topic.
- If quoting a previous message, trim off irrelevant parts.
- Use a descriptive Subject: field when starting a new topic.
- Do not use one message to ask two unrelated questions.
- Do NOT make the mistake of sending your completed lab
assignment to the mailing list.
This is not a joke; several students have made this mistake in
past semesters.
0.5: Grades
Your grade will be a function of your exams and laboratory
assignments (see below).
I am not yet sure of the exact weightings, but it will be
approximately 30% midterm, 30% labs, 40% final exam.
0.6: The Upper Left Board
I use the upper left board for lab/homework assignments and
announcements.
I should never erase that board.
If you see me start to erase an announcement, please let me know.
I try very hard to remember to write all announcements on the upper
left board and I am normally successful.
If, during class, you see
that I have forgotten to record something, please let me know.
HOWEVER, if I forgot and no one reminds me, the
assignment has still been given.
0.7: Homeworks and Labs
I make a distinction between homeworks and labs.
Labs are
- Required.
- Due several lectures later (date given on assignment).
- Graded and form part of your final grade.
- Penalized for lateness.
- Most often are computer programs you must write.
Homeworks are
- Optional.
- Due the beginning of the Next lecture.
- Not accepted late.
- Mostly from the book.
- Collected and returned.
- Able to help, but not hurt, your grade.
0.7.1: Homework Numbering
Homeworks are numbered by the class in which they are assigned.
So any homework given today is homework #1.
Even if I do not give homework today, the homework assigned next
class will be homework #2.
Unless I explicitly state otherwise, all homeworks assignments can
be found in the class notes.
So the homework present in the notes for lecture #n is homework #n
(even if I inadvertently forgot to write it to the upper left
board).
0.7.2: Doing Labs on non-NYU Systems
You may solve lab assignments on any system you wish, but ...
- You are responsible for any non-nyu machine.
I extend deadlines if the nyu machines are down, not if yours are.
- Be sure test your assignments to the nyu
systems.
In an ideal world, a program written in a high level language
like Java, C, or C++ that works on your system would also work
on the NYU system used by the grader.
Sadly this ideal is not always achieved despite marketing
claims to the contrary.
So, although you may develop you lab on any system,
you must ensure that it runs on the nyu system assigned to the
course.
- If somehow your assignment is misplaced by me and/or a grader,
we need a to have a copy ON AN NYU SYSTEM
that can be used to verify the date the lab was completed.
- When you complete a lab and have it on an nyu system, email the
lab to the grader and copy yourself on that message.
This email must come from your CIMS account.
Keep the copy until you have received your grade on the
assignment.
The systems support staff can retrieve your mail from their logs
given your copy and from that we can verify the dates.
I realize that I am being paranoid about this.
It is rare for labs to get misplaced, but they sometimes do and I
really don't want to be in the middle of an
I sent it ... I never received it
debate.
Thank you.
0.7.3: Obtaining Help with the Labs
Good methods for obtaining help include
- Asking me during office hours (see web page for my hours).
- Asking the mailing list.
- Asking another student, but ...
Your lab must be your own.
That is, each student must submit a unique lab.
Naturally, simply changing comments, variable names, etc. does
not produce a unique lab.
0.7.4: Computer Language Used for Labs
You may write your lab in Java, C, or C++.
Other languages may be possible, but please ask in advance.
I need to ensure that the TA is comfortable with the language.
0.8: A Grade of Incomplete
The rules for incompletes and grade changes are set by the school
and not the department or individual faculty member.
The rules set by CAS can be found in
http://cas.nyu.edu/object/bulletin0608.ug.academicpolicies.html
state:
The grade of I (Incomplete) is a temporary grade that
indicates that the student has, for good reason, not
completed all of the course work but that there is the
possibility that the student will eventually pass the
course when all of the requirements have been completed.
A student must ask the instructor for a grade of I,
present documented evidence of illness or the equivalent,
and clarify the remaining course requirements with the
instructor.
The incomplete grade is not awarded automatically. It is
not used when there is no possibility that the student
will eventually pass the course. If the course work is
not completed after the statutory time for making up
incompletes has elapsed, the temporary grade of I shall
become an F and will be computed in the student's grade
point average.
All work missed in the fall term must be made up by the end of the
following spring term.
All work missed in the spring term or in a summer session must be
made up by the end of the following fall term.
Students who are out
of attendance in the semester following the one in which the course
was taken have one year to complete the work.
Students should contact the College Advising Center for an Extension
of Incomplete Form, which must be approved by the
instructor.
Extensions of these time limits are rarely granted.
Once a final (i.e., non-incomplete) grade has been submitted by the
instructor and recorded on the transcript, the final grade cannot be
changed by turning in additional course work.
0.9: Academic Integrity Policy
The CS policy on academic integrity, which applies to all graduate
courses in the department, can be found
here
.
Appendix B: Logic Design
Remark: Appendix B is on the CD that comes with
the book, but is not in the book
itself.
If anyone does not have convenient access to a printer,
please let me know and I will print a black and white copy for you.
The pdf on the CD is in color so downloading it to your computer for
viewing in color is probably a good idea.
If you have a color printer that is not terribly slow, you might
want to print it in color—that's what I did.
Homework: Read B1
B.2: Gates, Truth Tables and Logic Equations
Homework: Read B2
The word digital, when used in digital logic
or
digital computer
means discrete.
That is, the electrical values (i.e., voltages) of the signals in a
circuit are treated as a non-negative integers (normally just 0 and
1).
The alternative is analog, where the electrical values are
treated as real numbers.
To summarize, we will use only two voltages: high and low.
A signal at the high voltage is referred to as 1
or true or set or asserted.
A signal at the low voltage is referred to as 0
or false or unset or deasserted.
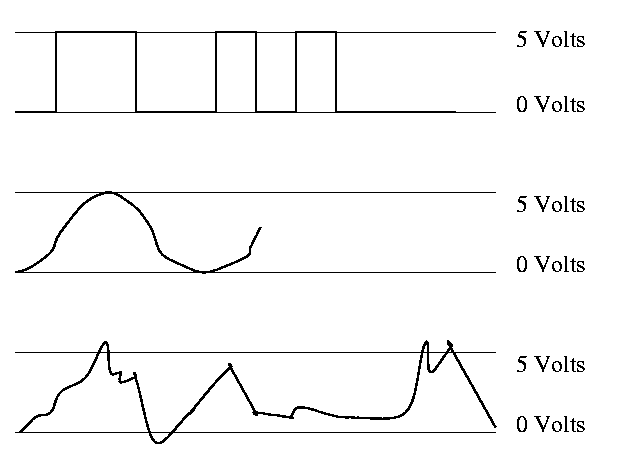
The assumption that at any time all signals are either 1 or 0 hides
a great deal of engineering.
- A full engineering design must make sure not to sample the
signal when not in one of these two states.
- Sometimes it is just a matter of waiting long enough
(determines the clock rate, i.e., how many megahertz).
- Other times it is worse and you must avoid glitches.
- Oscilloscope traces are shown on the right.
The vertical axis is voltage, the horizontal axis is time.
- Square wave—the ideal.
This is how we think of circuits.
- (Poorly drawn) Sine wave.
- Actual wave.
- Non-zero rise times and fall times.
- Overshoots and undershoots.
- Glitches.
Since this is not an engineering course, we will ignore these
issues and assume square waves.
In English digital implies 10 (based on digit, i.e. finger),
but not in computers.
Indeed, the word Bit is short for Binary digIT and binary means
base 2 not 10.
0 and 1 are called complements of each other as are true and false
(also asserted/deasserted; also set/unset)
A logic block can be thought of as a black box that takes signals in
and produces signals out.
There are two kinds of blocks
- Combinational (or combinatorial)
- Does NOT have memory elements.
- Is simpler than circuits with memory since the outputs are a
function of the inputs.
That is, if the same inputs are presented on
Monday and Tuesday, the same outputs will result.
- Sequential
- Contains memory.
- The current value in the memory is called the state of the block.
- The output depends on the input AND the state.
We are doing combinational blocks now. Will do sequential blocks
later (in a few lectures).
Truth Tables
Since combinatorial logic has no memory, it is simply a
(mathematical) function from its inputs to its outputs.
A common way to represent the function is using a
Truth Table.
A Truth Table has a column for each input and a
column for each output.
It has one row for each possible set of input values.
So, if there are A inputs, there are 2A rows.
In each of these rows the output columns have the output for that
input.
How many possible truth tables are there?
1-input, 1-output Truth Tables
 Let's start with a really simple truth table, one corresponding to a
logic block with one input and one output.
Let's start with a really simple truth table, one corresponding to a
logic block with one input and one output.
How many different truth tables are there for a
one input one output
logic block?
There are two columns (1 + 1) and two rows (21).
Hence the truth table looks like the one on the right with the
question marks filled in.
1-input, 1-output Truth Table
| In | Out |
|---|
|
|
| 0 | ? |
| 1 | ? |
Since there are two question marks and each one can have one of two
values there are just 22=4 possible truth tables.
- The constant function 1, which has output 1 (i.e., true) for either
input value.
- The constant function 0.
- The identity function, i.e., the function whose output equals
its input.
This logic block is sometimes called a buffer.
- An inverter.
This function has output the opposite of the input.
We will see pictures for the last two possibilities very soon.
2-input, 1-output Truth Table
| In1 | In2 | Out |
|---|
|
|
|
| 0 | 0 | ? |
| 0 | 1 | ? |
| 1 | 0 | ? |
| 1 | 1 | ? |
2-input, 1-output Truth Tables
Three columns (2+1) and 4 rows (22).
How many are there?
It is just the number ways can you fill in the
output entries, i.e. the question marks.
There are 4 output entries
so the answer is 24=16.
Larger Truth Tables
How about 2 in and 8 out?
- 10 cols.
- 22=4 rows.
- 4*8=32 question marks.
- 232 (about 4 billion) possibilities.
3 in and 8 out?
- 11 cols.
- 23=8 rows.
- 28*8=264 possibilities.
n in and k out?
- n+k cols.
- 2n rows.
- 2k*2n possibilities.
This gets big real fast!
Boolean algebra
We use a notation that looks like algebra to express logic functions and
expressions involving them.
The notation is called Boolean algebra in honor of
George Boole.
A Boolean value is a 1 or a 0.
A Boolean variable takes on Boolean values.
A Boolean function takes in boolean variables and
produces boolean values.
Four Boolean function are especially common.
- The (inclusive) OR Boolean function of two variables.
Draw its truth table on the board.
This is written + (e.g. X+Y where X and Y are Boolean variables)
and often called the logical sum.
(Three out of four output values in the truth table look
like the sum.)
- AND.
Draw its truth table on the board.
And is often called the logical product and written
as a centered dot (like the normal product in regular algebra).
I will offen write it as a period in these notes.
As in regular algebra, when all the logical variables are just one
character long, we indicate the product by juxtaposition, that
is, AB represents the product of A and B when it is clear that
it does not represent the two character symbol AB.
All four truth table values look like a product.
- NOT.
Draw its truth table on the board.
This is a unary operator (i.e., it has one argument, not two as
above; functions with two inputs are called binary operators).
Written A with a bar over it.
I will use ' instead of a bar as it is easier for me to input in
html.
- Exclusive OR (XOR).
Draw its truth table on the board.
Written as ⊕, a + with a circle around it.
True if exactly one input is true.
In particular, remember that TRUE ⊕ TRUE = FALSE.
Homework: Draw the truth table of the Boolean
function of 3 boolean variables that is true if and only
if exactly 1 of the three variables is true.
Some manipulation laws
Remember this is Boolean Algebra.
- Identity (recall that I use . for and):
- A+0 = 0+A = A
- A.1 = 1.A = A
- Inverse (recall that I use ' for not):
- A+A' = A'+A = 1
- A.A' = A'.A = 0
- The name inverse law is somewhat funny since you
Add the inverse and get the identity
for Product or Multiply by the
inverse and get the identity for Sum.
- Commutative Laws:
- A+B = B+A
- A.B = B.A
- Due to the commutative laws, we see that both the identity and
inverse laws contained redundancy.
For example from A+0 = A and the commutative law we get that
0+A = A without stating the latter explicitly.
- Associative Laws:
- A+(B+C) = (A+B)+C
- A.(B.C)=(A.B).C
- Due to the associative law we can write A.B.C without
parentheses since either order of evaluation gives the same
answer.
Similarly we can write A+B+C without parentheses.
- Distributive Laws:
- A(B+C)=AB+AC
- A+BC=(A+B)(A+C)
- Note that, unlike the situation for ordinary
algebra, both distributive laws are valid.
- Note also that like the situation for
ordinary algebra, multiplication has higher precedence than
addition if no parentheses are used.
- DeMorgan's Laws:
- (A+B)' = A'B' (NOT has the highest precedence
- (AB)' = A'+B'
How does one prove these laws??
- Simple (but long).
Write the truth tables for each side and see that the outputs
are the same.
Actually you write just one truth table with columns for all the
inputs and for the outputs of both sides.
You often write columns for intermediate outputs as well, but
that is only a convenience.
The key is that you have a column for the final value of the LHS
(left hand side) and a column for the final value of the RHS and
that these two columns have identical results.
- Prove the first distributive law on the board. The following
columns are required: the inputs A, B, C; the LHS A(B+C); and
the RHS AB+AC.
Beginners like us would also use columns for the intermediate
results B+C, AB, and AC.
Homework: Prove the second distributive law.
Homework: Prove DeMorgan's laws.
Let's do (on the board) the example on pages B-6 and B-7.
Consider a logic function with three inputs A, B, and C; and three
outputs D, E, and F defined as follows: D is true if
at least one input is true, E
if exactly two are true, and F if all three are
true.
(Note that by if
we mean if and only if
.
- Construct the truth table.
This is straightforward; simply fill in the 24 entries by
looking at the definitions of D, E, and F.
- Produce logic equations for D, E, and F.
This can be done in two ways.
- Examine the column of the truth table for a given output
and write one term for each entry that is a 1.
This method requires constructing the truth table and might
be called the method of perspiration.
- Look at the definition of D, E, and F and just
figure it out
.
This might be called the method of inspiration.
For D and F it is fairly clear.
E requires some cleverness: the key idea is that
exactly two are true
is the same as
(at least) two are true AND it is not the case that
all three are true
.
So we have the AND of two expressions: the first is a three
way OR and the second the negation of a three way AND.


 Let's start with a really simple truth table, one corresponding to a
logic block with one input and one output.
Let's start with a really simple truth table, one corresponding to a
logic block with one input and one output.