We must prevent interleaving sections of code that need to be atomic with respect to each other. That is, the conflicting sections need mutual exclusion. If process A is executing its critical section, it excludes process B from executing its critical section. Conversely if process B is executing is critical section, it excludes process A from executing its critical section.
Requirements for a critical section implementation.
The operating system can choose not to preempt itself. That is, we do not preempt system processes (if the OS is client server) or processes running in system mode (if the OS is self service). Forbidding preemption for system processes would prevent the problem above where x<--x+1 not being atomic crashed the printer spooler if the spooler is part of the OS.
But simply forbidding preemption while in system mode is not sufficient.
Initially P1wants=P2wants=false
Code for P1 Code for P2
Loop forever { Loop forever {
P1wants <-- true ENTRY P2wants <-- true
while (P2wants) {} ENTRY while (P1wants) {}
critical-section critical-section
P1wants <-- false EXIT P2wants <-- false
non-critical-section } non-critical-section }
Explain why this works.
But it is wrong! Why?
Let's try again. The trouble was that setting want before the loop permitted us to get stuck. We had them in the wrong order!
Initially P1wants=P2wants=false
Code for P1 Code for P2
Loop forever { Loop forever {
while (P2wants) {} ENTRY while (P1wants) {}
P1wants <-- true ENTRY P2wants <-- true
critical-section critical-section
P1wants <-- false EXIT P2wants <-- false
non-critical-section } non-critical-section }
Explain why this works.
But it is wrong again! Why?
So let's be polite and really take turns. None of this wanting stuff.
Initially turn=1
Code for P1 Code for P2
Loop forever { Loop forever {
while (turn = 2) {} while (turn = 1) {}
critical-section critical-section
turn <-- 2 turn <-- 1
non-critical-section } non-critical-section }
This one forces alternation, so is not general enough. Specifically, it does not satisfy condition three, which requires that no process in its non-critical section can stop another process from entering its critical section. With alternation, if one process is in its non-critical section (NCS) then the other can enter the CS once but not again.
The first example violated rule 4 (the whole system blocked). The second example violated rule 1 (both in the critical section. The third example violated rule 3 (one process in the NCS stopped another from entering its CS).
In fact, it took years (way back when) to find a correct solution. Many earlier “solutions” were found and several were published, but all were wrong. The first correct solution was found by a mathematician named Dekker, who combined the ideas of turn and wants. The basic idea is that you take turns when there is contention, but when there is no contention, the requesting process can enter. It is very clever, but I am skipping it (I cover it when I teach distributed operating systems in V22.0480 or G22.2251). Subsequently, algorithms with better fairness properties were found (e.g., no task has to wait for another task to enter the CS twice).
What follows is Peterson's solution, which also combines turn and wants to force alternation only when there is contention. When Peterson's solution was published, it was a surprise to see such a simple soluntion. In fact Peterson gave a solution for any number of processes. A proof that the algorithm satisfies our properties (including a strong fairness condition) for any number of processes can be found in Operating Systems Review Jan 1990, pp. 18-22.
Initially P1wants=P2wants=false and turn=1
Code for P1 Code for P2
Loop forever { Loop forever {
P1wants <-- true P2wants <-- true
turn <-- 2 turn <-- 1
while (P2wants and turn=2) {} while (P1wants and turn=1) {}
critical-section critical-section
P1wants <-- false P2wants <-- false
non-critical-section non-critical-section
The word atomically means that the two actions performed by TAS(x), testing (i.e., returning the old value of x) and setting (i.e., assigning true to x) are inseparable. Specifically it is not possible for two concurrent TAS(x) operations to both return false (unless there is also another concurrent statement that sets x to false).
With TAS available implementing a critical section for any number of processes is trivial.
loop forever {
while (TAS(s)) {} ENTRY
CS
s<--false EXIT
NCS
Remark: Tanenbaum does both busy waiting (as above) and blocking (process switching) solutions. We will only do busy waiting, which is easier. Sleep and Wakeup are the simplest blocking primitives. Sleep voluntarily blocks the process and wakeup unblocks a sleeping process. We will not cover these.
Homework: Explain the difference between busy waiting and blocking process synchronization.
Remark: Tannenbaum use the term semaphore only for blocking solutions. I will use the term for our busy waiting solutions. Others call our solutions spin locks.
The entry code is often called P and the exit code V. Thus the critical section problem is to write P and V so that
loop forever
P
critical-section
V
non-critical-section
satisfies
Note that I use indenting carefully and hence do not need (and sometimes omit) the braces {} used in languages like C or java.
A binary semaphore abstracts the TAS solution we gave for the critical section problem.
while (S=closed) {}
S<--closed <== This is NOT the body of the while
where finding S=open and setting S<--closed is atomic
The above code is not real, i.e., it is not an implementation of P. It is, instead, a definition of the effect P is to have.
To repeat: for any number of processes, the critical section problem can be solved by
loop forever
P(S)
CS
V(S)
NCS
The only specific solution we have seen for an arbitrary number of processes is the one just above with P(S) implemented via test and set.
Remark: Peterson's solution requires each process to know its processor number. The TAS soluton does not. Moreover the definition of P and V does not permit use of the processor number. Thus, strictly speaking Peterson did not provide an implementation of P and V. He did solve the critical section problem.
To solve other coordination problems we want to extend binary semaphores.
Both of the shortcomings can be overcome by not restricting ourselves to a binary variable, but instead define a generalized or counting semaphore.
while (S=0) {}
S--
where finding S>0 and decrementing S is atomic
These counting semaphores can solve what I call the semi-critical-section problem, where you premit up to k processes in the section. When k=1 we have the original critical-section problem.
initially S=k
loop forever
P(S)
SCS <== semi-critical-section
V(S)
NCS
Initially e=k, f=0 (counting semaphore); b=open (binary semaphore)
Producer Consumer
loop forever loop forever
produce-item P(f)
P(e) P(b); take item from buf; V(b)
P(b); add item to buf; V(b) V(e)
V(f) consume-item
| Busy wait | block/switch | |
|---|---|---|
| critical | (binary) semaphore | (binary) semaphore |
| semi-critical | counting semaphore | counting semaphore |
| Busy wait | block/switch | |
|---|---|---|
| critical | enter/leave region | mutex |
| semi-critical | no name | semaphore |
We did this previously.
A classical problem from Dijkstra
The purpose of mentioning the Dining Philosophers problem without giving the solution is to give a feel of what coordination problems are like. The book gives others as well. We are skipping these (again this material would be covered in a sequel course). If you are interested look, for example, here.
Homework: 31 and 32 (these have short answers but are not easy). Note that the problem refers to fig. 2-20, which is incorrect. It should be fig 2-33.
Quite useful in multiprocessor operating systems and database systems. The “easy way out” is to treat all processes as writers in which case the problem reduces to mutual exclusion (P and V). The disadvantage of the easy way out is that you give up reader concurrency. Again for more information see the web page referenced above.
We then defined (binary) Semaphores and showed that a Semaphore easily solves the critical section problem and doesn't require knowledge of how many processes are competing for the critical section. We gave an implementation using Test-and-Set.
We then gave an operational definition of Semaphore (which is not an implementation) and morphed this definition to obtain a Counting (or Generalized) Semaphore, for which we gave NO implementation. I asserted that a counting semaphore can be implemented using 2 binary semaphores and gave a reference.
We defined the Readers/Writers (or Bounded Buffer) Problem and showed that it can be solved using counting semaphores (and binary semaphores, which are a special case).
Finally we briefly discussed some classical problem, but did not give (full) solutions.
Scheduling processes on the processor is often called “process scheduling” or simply “scheduling”.
The objectives of a good scheduling policy include
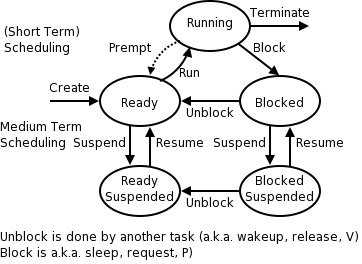
Recall the basic diagram describing process states
For now we are discussing short-term scheduling, i.e., the arcs connecting running <--> ready.
Medium term scheduling is discussed later.
It is important to distinguish preemptive from non-preemptive scheduling algorithms.
This is used for real time systems. The objective of the scheduler is to find a schedule for all the tasks (there are a fixed set of tasks) so that each meets its deadline. The run time of each task is known in advance.
Actually it is more complicated.
We do not cover deadline scheduling in this course.
There is an amazing inconsistency in naming the different (short-term) scheduling algorithms. Over the years I have used primarily 4 books: In chronological order they are Finkel, Deitel, Silberschatz, and Tanenbaum. The table just below illustrates the name game for these four books. After the table we discuss each scheduling policy in turn.
Finkel Deitel Silbershatz Tanenbaum ------------------------------------- FCFS FIFO FCFS FCFS RR RR RR RR PS ** PS PS SRR ** SRR ** not in tanenbaum SPN SJF SJF SJF PSPN SRT PSJF/SRTF -- unnamed in tanenbaum HPRN HRN ** ** not in tanenbaum ** ** MLQ ** only in silbershatz FB MLFQ MLFQ MQ
Remark: For an alternate organization of the scheduling algorithms (due to Eric Freudenthal and presented by him Fall 2002) click here.
If the OS “doesn't” schedule, it still needs to store the list of ready processes in some manner. If it is a queue you get FCFS. If it is a stack (strange), you get LCFS. Perhaps you could get some sort of random policy as well.
The round robin was originally a petition, its signatures arranged in a circular form to disguise the order of signing. Most probably it takes its name from the "ruban rond," "round ribbon," in 17th-century France, where government officials devised a method of signing their petitions of grievances on ribbons that were attached to the documents in a circular form. In that way no signer could be accused of signing the document first and risk having his head chopped off for instigating trouble. "Ruban rond" later became "round robin" in English and the custom continued in the British navy, where petitions of grievances were signed as if the signatures were spokes of a wheel radiating from its hub. Today "round robin" usually means a sports tournament where all of the contestants play each other at least once and losing a match doesn't result in immediate elimination.
Encyclopedia of Word and Phrase Origins by Robert Hendrickson (Facts on File, New York, 1997).
Homework: 26, 35, 38.
Homework: Give an argument favoring a large quantum; give an argument favoring a small quantum.
| Process | CPU Time | Creation Time |
|---|---|---|
| P1 | 20 | 0 |
| P2 | 3 | 3 |
| P3 | 2 | 5 |
Homework: Redo the previous homework for q=2 with the following change. After process P1 runs for 3ms (milliseconds), it blocks for 2ms. P1 never blocks again. P2 never blocks. After P3 runs for 1 ms it blocks for 1ms. Remind me to answer this one in class next lecture.
Merge the ready and running states and permit all ready jobs to be run at once. However, the processor slows down so that when n jobs are running at once, each progresses at a speed 1/n as fast as it would if it were running alone.
Homework: 34.