Compilers

Production	Semantic Rule
A → B C	B.inh = A.inh C.ihn = A.inh - B.inh + B.syn A.syn = A.inh * B.inh + B.syn - C.inh / C.syn
B → X	X.inh = something B.syn = B.inh + X.syn
C → Y	Y.inh = something C.syn = C.inh + Y.syn

Evaluating L-Attributed Definitions

The table on the right shows a very simple production with fairly general, L-attributed semantic rules attached. Compare the dependencies with the general case shown in the (red-green) picture of L-attributed SDDs above.

The picture below the table shows the parse tree for the grammar in the table. The triangles below B and C represent the parse tree for X and Y. The dotted and numbered arrow in the picture illustrates the evaluation order for the attributes; it will be discussed shortly.

The rules for calculating A.syn, B.inh, and C.inh are shown in the table. The attribute A.inh would have been set by the parent of A in the tree; the semantic rule generating A.h would be given with the production at the parent. The attributes X.syn and Y.syn are calculated at the children of B and C respectively. X.syn can depend of B.inh and on values in the triangle below B; similarly for Y.syn.

The picture shows that there is an evaluation order for L-attributed definitions (again assuming no case 3). We just need to follow the arrow and stop at all the numbered points. As in the pictures above red signifies inherited attributes and green synthetic. Specifically, the evaluations at the numbered stops are

1. A is invoked (viewing the traversal as a program) and is passed its inherited attributes (A.inh in our case, but of course there could be several such attributes), which have been evaluated at its parent.
2. B is invoked by A and is given B.inh, which A has calculated. In programming terms: A executes
         call B(B.inh)
   where the argument has been evaluated by A. This argument can depend on A.inh since the parent of A has given A this value.
3. B calls its first child (in our example X is the only child) and passes to the child its inherited attributes.
4. The child returns passing back to B. the synthesized attributes of the child. In programming terms: X executes
         return X.syn
   In reality there could be more synthesized attributes, there could be more children, the children could have children, etc.
5. B returns to A passing back B.syn, which can depend on B.inh (given to B by A in step 2) and X.syn (given to B by X in the previous step).
6. A calls C giving C its inherited attributes, which can depend on A.ihn (given to A, by A's parent), B.inh (previously calculated by A in step 2), and B.syn (given to A by B in step 5).
7. C calls its first child, just as B did.
8. The child returns to C, just as B's child returned to B.
9. C returns to A passing back C.syn, just as B did.
10. A returns to its parent passing back A.syn, which can depend on A.inh (given to A by its parent in step 1), B.inh calculated by A in step 2, B.syn (given to A by B in step 5), C.inh (calculated by A in step 6), and C.syn (given to A by C in step 9).

More formally, do a depth first traversal of the tree and evaluate inherited attributes on the way down and synthetic attributes on the way up. This corresponds to a an Euler-tour traversal. It also corresponds to a call graph of a program where actions are taken at each call and each return

The first time you visit a node (on the way down), evaluate its inherited attributes. The second time you visit a node (on the way back up), you evaluate the synthesized attributes.

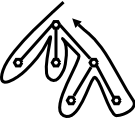
The key point is that all attributes needed will have already been evaluated. Consider the rightmost child of the root in the diagram on the right.

1. Inherited attributes (which are evaluated on the first, i.e., downward, pass): An inherited attribute depends only on inherited attributes from the parent and on (inherited or synthesized) attributes from left siblings.
   • The parent will have already been evaluated on the downward pass before the current child so the parent's inherited attributes will have already been evaluated.
   • The left children have already had both passes done so all their attributes will have been evaluated.
2. Synthesized attributes (which are evaluated on the second, i.e., upward pass): A synthesized attribute depends only on (inherited or synthesized) attributes of its children and on its own inherited attributes.
   • The children have already had both passes so all their attributes have been evaluated.
   • The node itself has already had its first (downward) pass so has had its inherited attributes evaluated.

Homework: 3(a-c).

5.2.5: Semantic Rules with Controlled Side Effects

When we have side effects such as printing or adding an entry to a table we must ensure that we have not added a constraint to the evaluation order that causes a cycle.

For example, the left-recursive SDD shown in the table on the right propagates type information from a declaration to entries in an identifier table.

The function addType adds the type information in the second argument to the identifier table entry specified in the first argument. Note that the side effect, adding the type info to the table, does not affect the evaluation order.

Draw the dependency graph on the board. Note that the terminal ID has an attribute (given by the lexer) entry that gives its entry in the identifier table. The nonterminal L has (in addition to L.type) a dummy synthesized attribute, say AddType, that is a place holder for the addType() routine. AddType depends on the arguments of addType(). Since the first argument is from a child, and the second is an inherited attribute of this node, we have legal dependences for a synthesized attribute.

Note that we have an L-attributed definition.

Homework: For the SDD above, give the annotated parse tree for

    INT a,b,c
  

5.3: Applications of Syntax-Directed Translations

5.3.1: Construction of Syntax Trees

Production	Semantic Rules
E → E 1 + T	E.node = new Node('+',E1.node,T.node)
E → E 1 - T	E.node = new Node('-',E1.node,T.node)
E → T	E.node = T.node
T → ( E )	T.node = E.node
T → ID	T.node = new Leaf(ID,ID.entry)
T → NUM	T.node = new Leaf(NUM,NUM.val)

Recall that in syntax tree (technically an abstract syntax tree) has just the essentials. For example 7+3*5, would have one + node, one *, and the three numbers. Lets see how to construct the syntax tree from an SDD.

Assume we have two functions Leaf(op,val) and Node(op,c1,...,cn), that create leaves and interior nodes respectively of the syntax tree. Leaf is called for terminals. Op is the label of the node (op for operation) and val is the lexical value of the token. Node is called for nonterminals and the ci's refer (are pointers) to the children.

Production	Semantic Rules	Type
E → T E'	E.node=E'.syn	Synthesized
	E'node=T.node	Inherited
E' → + T E'1	E'1.node=new Node('+',E'.node,T.node)	Inherited
	E'.syn=E'1.syn	Synthesized
E' → - T E'1	E'1.node=new Node('-',E'.node,T.node)	Inherited
	E'.syn=E'1.syn	Synthesized
E' → ε	E'.syn=E'.node	Synthesized
T → ( E )	T.node=E.node	Synthesized
T → ID	T.node=new Leaf(ID,ID.entry)	Synthesized
T → NUM	T.node=new Leaf(NUM,NUM.val)	Synthesized

The upper table on the right shows a left-recursive grammar that is S-attributed (so all attributes are synthesized).

Try this for x-2+y and see that we get the syntax tree.

When we eliminate the left recursion, we get the lower table on the right. It is a good illustration of dependencies. Follow it through and see that you get the same syntax tree as for the left-recursive version.

Remarks:

1. You probably did/are-doing/will-do some variant of new Node and new Leaf for lab 3. When processing a production
   1. Create a parse tree node for the LHS.
   2. Call subroutines for RHS symbols and connect the resulting nodes to the node created in i.
   3. Return a reference to the new node so the parent can hook it into the parse tree.
2. It is the lack of a call to new in the third and fourth productions that causes the (abstract) syntax tree to be produced rather than the parse (concrete syntax) tree.
3. Production compilers do not produce a parse tree, but only the syntax tree. The syntax tree is smaller, and hence more (space and time) efficient for subsequent passes that walk the tree. The parse tree is (I believe) slightly easier to construct as you don't have to decide which nodes to produce; you simply produce them all.

5.3.2: The structure of a Type

This course emphasizes top-down parsing (at least for the labs) and hence we must eliminate left recursion. The resulting grammars often need inherited attributes, since operations and operands are in different productions. But sometimes the language itself demands inherited attributes. Consider two ways to declare a 3x4, two-dimensional array.

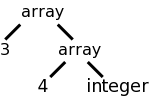
    array [3] of array [4] of int    and     int[3][4]
  

Assume that we want to produce a tree structure like the one the right for the array declarations on the left. The tree structure is generated by calling a function array(num,type). Our job is to create an SDD so that the function gets called with the correct arguments.

For the first language representation of arrays (found in Ada and in lab 3), it is easy to generate an S-attributed (non-left-recursive) grammar based on
A → ARRAY [ NUM ] OF A | INT | REAL
This is shown in the table on the left.

Production	Semantic Rules	Type
T → B C	T.t=C.t	Synthesized
	C.b=B.t	Inherited
B → INT	B.t=integer	Synthesized
B → REAL	B.t=real	Synthesized
C → [ NUM ] C1	C.t=array(NUM.val,C1.t)	Synthesized
	C1.b=C.b	Inherited
C → ε	C.t=C.b	Synthesized

Production	Semantic Rule
A → ARRAY [ NUM ] OF A1	A.t=array(NUM.val,A1.t)
A → INT	A.t=integer
A → REAL	A.t=real

On the board draw the parse tree and see that simple synthesized attributes above suffice.

For the second language representation of arrays (the C-style), we need some smarts (and some inherited attributes) to move the int all the way to the right. Fortunately, the result, shown in the table on the right, is L-attributed and therefore all is well.

Homework: 1.

5.4: Syntax-Directed Translation Schemes (SDTs)

Basically skipped.

The idea is that instead of the SDD approach, which requires that we build a parse tree and then perform the semantic rules in an order determined by the dependency graph, we can attach semantic actions to the grammar (as in chapter 2) and perform these actions during parsing, thus saving the construction of the parse tree.

But except for very simple languages, the tree cannot be eliminated. Modern commercial quality compilers all make multiple passes over the tree, which is actually the syntax tree (technically, the abstract syntax tree) rather than the parse tree (the concrete syntax tree).

5.4.1: Postfix Translation Schemes

If parsing is done bottom up and the SDD is S-attributed, one can generate an SDT with the actions at the end (hence, postfix). In this case the action is perform at the same time as the RHS is reduced to the LHS.

5.4.2: Parser-Stack Implementation of Postfix SDTs

Skipped.

5.4.3: SDTs with Actions Inside Productions

Skipped

5.4.4: Eliminating Left Recursion from SDTs

Skipped

5.4.5: SDTs For L-Attributed Definitions

Skipped

5.5: Implementing L-Attributed SDD's

A good summary of the available techniques.

1. Build the parse tree and annotate. Works as long as no cycles are present (guaranteed by L- or S-attributed).
2. the parse tree, add actions, and execute the actions in preorder. Works for any L-attributed definition. Can add actions based on the semantic rules of the SDD. (Since actions are leaves of the tree, I don't see why preorder is relevant).
3. Translate During Recursive Descent Parsing. See below.
4. Generate Code on the Fly. Also uses recursive descent, but is restrictive.
5. Implement an SDT during LL-parsing. Skipped.
6. Implement an SDT during LR-parsing of an LL Language. Skipped.

5.5.1: Translation During Recursive-Descent Parsing

Recall that in recursive-descent parsing there is one procedure for each nonterminal. Assume the SDD is L-attributed. Pass the procedure the inherited attributes it might need (different productions with the same LHS need different attributes). The procedure keeps variables for attributes that will be needed (inherited for nonterminals in the body; synthesized for the head). Call the procedures for the nonterminals. Return all synthesized attributes for this nonterminal.

5.5.2: On-the-fly Code Generation

5.5.3: L-attributed SDDs and LL Parsing

5.5.4: Bottom-Up Parsing of L-Attributed SDDs

Requires an LL (not just LR) language.

What is this all used for?

Assume we have a parse tree as produced, for example, by your lab3. You now want to write the semantics analyzer, or intermediate code generator, and you have these semantic rules or actions that need to be performed. Assume the grammar is L-attributed, so we don't have to worry about dependence loops.

You start to write
      analyze (tree-node)
This procedure is basically a big switch statement where the cases correspond to the different productions in the grammar. The tree-node is the LHS of the production and the children are the RHS. So by first switching on the tree-node and then inspecting enough of the children, you can tell the production.

As described in 5.5.1 above, you have received as parameters (in addition to tree-node), the attributes you inherit. You then call yourself recursively, with the tree-node argument set to your leftmost child, then call again using the next child, etc. Each time, you pass to the child the attributes it inherits.

When each child returns, it passes back its synthesized attributes.

After the last child returns, you return to your caller, passing back the synthesized attributes you have calculated.

Variations

1. Instead of a giant switch, you could have separate routines for each nonterminal as done in the parser and just switch on the productions having this nonterminal as LHS.
2. You could have separate routines for each production (requires the child tree node to indicate the production it corresponds to, not just the nonterminal, i.e. not just the LHS of the production).
3. If you like actions instead of rules, perform the actions where indicated in the SDT.
4. Global variable can be used (with care) instead of parameters.
5. As illustrated earlier, you can call routines instead of setting an attribute (see addType in 5.2.5).

Chapter 6: Intermediate-Code Generation

Homework: Read Chapter 6.

6.1: Variants of Syntax Trees

6.1.1: Directed Acyclic Graphs for Expressions

The difference between a syntax DAG and a syntax tree is that the former can have undirected cycles. DAGs are useful where there are multiple, identical portions in a given input. The common case of this is for expressions where there often are common subexpressions. For example in the expression
      X + a + b + c - X + ( a + b + c )
each individual variable is a common subexpression. But a+b+c is not since the first occurrence has the X already added. This is a real difference when one considers the possibility of overflow or of loss of precision. The easy case is
      x + y * z * w - ( q + y * z * w )
where y*z*w is a common subexpression.

It is easy to find such common subexpressions. The constructor Node() above checks if an identical node exists before creating a new one. So Node ('/',left,right) first checks if there is a node with op='/' and children left and right. If so, a reference to that node is returned; if not, a new node is created as before.

Homework: 1.

6.1.2: The Value-Number Method for Constructing DAGS

Often one stores the tree or DAG in an array, one entry per node. Then the array index, rather than a pointer, is used to reference a node. This index is called the node's value-number and the triple
    <op, value-number of left, value-number of right>
is called the signature of the node. When Node(op,left,right) needs to determine if an identical node exists, it simply searches the table for an entry with the required signature.

Searching an unordered array is slow; there are many better data structures to use. Hash tables are a good choice.

Homework: 2.