Homework: Read Chapter 5.
Again we are redoing, more formally and completely, things we briefly discussed when breezing over chapter 2.
Recall that a syntax-directed definition (SDD) adds semantic rules
to the productions of a grammar.
For example to the production T → T1 / F we might add the rule
T.code = T1.code || F.code || '/'
if we were doing an infix to postfix translator.
Rather than constantly copying ever larger strings to finally
output at the root of the tree after a depth first traversal, we can
perform the output incrementally by embedding semantic actions
within the productions themselves.
The above example becomes
T → T1 / F { print '/' }
Since we are generating postfix, the action comes at the end (after we have generated the subtrees for T1 and F, and hence performed their actions). In general the actions occur within the production, not necessarily after the last symbol.
For SDD's we conceptually need to have the entire tree available after the parse so that we can run the postorder traversal. (It is postorder since we are doing postfix; we will see other orders shortly.) Semantic actions can be performed during the parse, without saving the tree.
Formally, attributes are values (of any type) that are associated with grammar symbols. Write X.a for the attribute a of symbol X. You can think of attributes as fields in a record/struct/object.
Semantic rules (rules for short) are associated with productions.
Terminals can have synthesized attributes; these are given to it by the lexer (not the parser). There are no rules in an SDD giving values to attributes for terminals. Terminals do not have inherited attributes.
A nonterminal A can have both inherited and synthesized attributes. The difference is how they are computed. In either the computation is specified by a rule associated with the production at a node N of the parse tree.
Definition: A synthesized attribute of a nonterminal A, is defined at a node N (where A is the LHS of the production associated with N). The attribute can depend only on (synthesized or inherited) attribute values at the children of N (the RHS of N) and on inherited attribute values at N itself.
The arithmetic division example above was synthesized.
| Production | Semantic Rules |
|---|---|
| L → E $ | L.val = E.val |
| E → E1 + T | E.val = E1.val + T.val |
| E → E1 - T | E.val = E1.val - T.val |
| E → T | E.val = T.val |
| T → T1 * F | T.val = T1.val * F.val |
| T → T1 / F | T.val = T1.val / F.val |
| T → F | T.val = F.val |
| F → ( E ) | F.val = E.val |
| F → num | F.val = num.lexval |
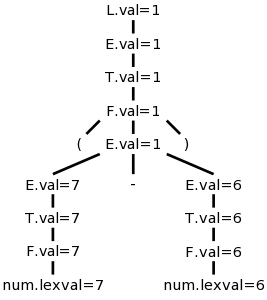
Example: The SDD at the right gives a left-recursive grammar for expressions with an extra nonterminal L added as the start symbol. The terminal num is given a value by the lexer, which corresponds to the value stored in the numbers table for lab 2.
Draw the parse tree for 7+6/3 on the board and verify that L.val is 9, the value of the expression.
Definition: This example use only synthesized attributes; such SDDs are called S-attributed and have the property that the rules give the attribute of the LHS in terms of attributes of the RHS.
For an S-attributed SDD, all the rules can be evaluated by a single bottom-up (i.e., postorder) traversal of the annotated parse tree.
Inherited attributes are more complicated since the node N of the parse tree with which the attribute is associated (and which is also the natural node to store the value) does not contain the production with the corresponding semantic rule.
Definition: An inherited attribute of a nonterminal B at node N (where B is the LHS) is defined by a semantic rule of the production at the parent of N (where B occurs in the RHS). The value depends only on attributes at N, N's siblings, and N's parent.
Note that when viewed from the parent node P (the site of the semantic rule), the inherited attribute depends on values at P and at P's children (the same as for synthesized attributes). However, and this is crucial, the nonterminal B is the LHS of a child of P and hence the attribute is naturally associated with that child. It is possibly stored there and is shown there in the diagrams below.
We will see an example with inherited attributes soon.
Definition: Often the attributes are just evaluations without side effects. In such cases we call the SDD an attribute grammar.
If we are given an SDD and a parse tree for a given sentence, we would like to evaluate the annotations at every node. Since, for synthesized annotations parents can depend on children, and for inherited annotations children can depend on parents, there is no guarantee that one can in fact find an order of evaluation. The simplest counterexample is the single production A→B with synthesized attribute A.syn, inherited attribute B.inh, and rules A.syn=B.inh and B.inh=A.syn+1. This means to evaluate A.syn at the parent node we need B.inh at the child and vice versa. Even worse it is very hard to tell, in general, if every sentence has a successful evaluation order.
All this not withstanding we will not have great difficulty because we will not be considering the general case.
Recall that a parse tree has leaves that are terminals and internal
nodes that are non-terminals.
We when we decorate the parse tree with attributes, the result is
called an annotated parse tree, which is constructed as
follows.
Each internal node corresponds to a production with the symbol
labeling the node the LHS of the production.
If there are no attributes for the LHS in this production, we leave
the node as it was (I don't believe this is a common occurrence).
If there are k attributes for the LHS, we replace the LHS in the
parse tree by k equations.
The LHS of the equation is the attribute and the right hand side is
its value.
Note that the annotated parse tree contains all the information of
the original parse tree since we replaced something like E with
something like E.att=7
.
We computed the values to put in this tree for 7+6/3 and on the right is (7-6).
Homework: 5.1
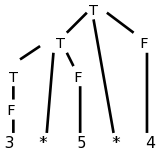
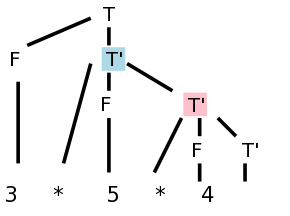
Consider the following left-recursive grammar for multiplication of numbers and the parse tree on the right for 3*5*4.
T → T * F T → F F → num
It is easy to see how the values can be propagated up the tree and the expression evaluated.
When doing top-down parsing, we need to avoid left recursion.
Consider the grammar below, which is the result of removing
the left recursion, and again its parse tree is shown on the right.
Try not to look at the semantic rules for the moment.

| Production | Semantic Rules | Type |
|---|---|---|
| T → F T' | T'.lval = F.val | Inherited |
| T.val = T'.tval | Synthesized | |
| T' → * F T1' | T'1.lval = T'.lval * F.val | Inherited |
| T'.tval = T'1.tval | Synthesized | |
| T' → ε | T'.tval = T'.lval | Synthesized |
| F → num | F.val = num.lexval | Synthesized |
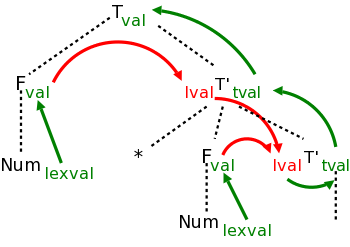
Now where on the tree should we do the multiplication 3*5? There is no node that has 3 and * and 5 as children. The second production is the one with the * so that is the natural candidate for the multiplication site. Make sure you see that this production (for 3*5) is associated with the blue highlighted node in the parse tree. The right operand (5) can be obtained from the F that is the middle child of this T'. F gets the value from its child, the number itself; this is an example of the simple synthesized case we have already seen, F.val=num.lexval (see the last semantic rule in the table).
But where is the left operand?
It is located at the sibling of T' in the parse tree, i.e., at the F
immediately to T's left.
This F is not mentioned in the production associated with the
T' node we are examining.
So, how does T' get F.val from its sibling?
The common parent, in this case T, can get the value from F and then our
node can inherit the value from its parent.
Bingo! ... an inherited attribute.
This can be accomplished by having the following two rules at the
node T.
T.tmp = F.val
T'.lval = T.tmp
Since we have no other use for T.tmp, we combine the above two rules into the first rule in the table.
Now lets look at the second multiplication (3*5)*4, where the parent of T' is another T'. (This is the normal case. When there are n multiplies, n-1 have T' as parent and only one has T).
The red-highlighted T' is the site for the multiplication. However, it needs as left operand, the product 3*5 that its parent can calculate. So we have the parent (another T' node, the blue one in this case) calculate the product and store it as an attribute of its right child namely the red T'. That is the first rule for T' in the table.
We have now explained the first, third, and last semantic rules. These are enough to calculate the answer. Indeed, if we trace it through, 60 does get evaluated and stored in the bottom right T', the one associated with the ε-production. Our remaining goal is to get the value up to the root where it represents the evaluation of this term T and can be combined with other terms to get the value of a larger expression.
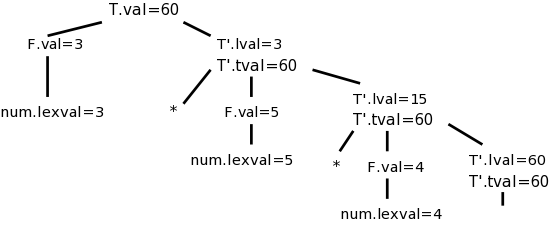
Going up is easy, just synthesize. I named the attribute tval, for term-value. It is generated at the ε-production from the lval attribute (which at this node is not a good name) and propagated back up. At the T node it is called simply val. At the right we see the annotated parse tree for this input.
Homework: Extend this SDD to handle the left-recursive, more complete expression evaluator given earlier in this section. Don't forget to eliminate the left recursion first.
It clearly requires some care to write the annotations.
Another question is how does the system figure out the evaluation order if one exists? That is the subject of the next section.
Remark: Consider the identifier table. The lexer creates it initially, but as the compiler performs semantic analysis and discovers more information about various identifiers, e.g., type and visibility information, the table is updated. One could think of this is some inherited/synthesized attribute pair that during each phase of analysis is pushed down and back up the tree. However, it is not implemented this way; the table is made a global data structure that is simply updated. The the compiler writer must ensure manually that the updates are performed in an order respecting any dependences.
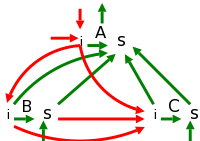
The diagram on the right illustrates a great deal. The black shows the parse tree for the multiplication grammar just studied when applied to a single multiplication, e.g. 3*5. The synthesized attributes are shown in green and are written to the right of the grammar symbol at the node where they are defined. The inherited attributes are shown in red and are written to the left of the grammar symbol where it is defined.
Each green arrow points to the attribute calculated from the attribute at the tail of the arrow. These arrows either go up the tree one level or stay at a node. That is because a synthesized attribute can depend only on the node where it is defined and that node's children. The computation of the attribute is associated with the production at the node at its arrowhead. In this example, each synthesized attribute depends on only one other, but that is not required.
Each red arrow also points to the attribute calculated from the attribute at the tail. Note that two red arrows point to the same attribute. This indicates that the common attribute at the arrowheads, depends on both attributes at the tails. According to the rules for inherited attributes, these arrows either go down the tree one level, go from a node to a sibling, or stay within a node. The computation of the attribute is associated with the production at the parent of the node at the arrowhead.
The graph just drawn is called the dependency graph. In addition to being generally useful in recording the relations between attributes, it shows the evaluation order(s) that can be used. Since the attribute at the head of an arrow depends on the on the one at the tail, we must evaluate the head attribute after evaluating the tail attribute.
Thus what we need is to find an evaluation order respecting the arrows. This is called a topological sort. The rule is that the needed ordering can be found if and only if there are no (directed) cycles. The algorithm is simple.
If the algorithm succeeds in deleting all the nodes, then the deletion order is a suitable evaluation order and there were no directed cycles.
The topological sort algorithm is nondeterministic (Choose a node) and hence there can be many topological sort orders.
Homework: 1.
Given an SDD and a parse tree, it is easy to tell (by doing a topological sort) whether a suitable evaluation exists (and to find one).
However, a very difficult problem is, given an SDD, are there any parse trees with cycles in their dependency graphs, i.e., are there suitable evaluation orders for all parse trees. Fortunately, there are classes of SDDs for which a suitable evaluation order is guaranteed.
As mentioned above an SDD is S-attributed if every attribute is synthesized. For these SDDs all attributes are calculated from attribute values at the children since the other possibility, the tail attribute is at the same node, is impossible since the tail attribute must be inherited for such arrows. Thus no cycles are possible and the attributes can be evaluated by a postorder traversal of the parse tree.
Since postorder corresponds to the actions of an LR parser when reducing the body of a production to its head, it is often convenient to evaluate synthesized attributes during an LR parse.
Unfortunately, it is hard to live without inherited attributes.
So we define a class that permits certain kinds of inherited
attributes.
Definition: An SDD is L-Attributed if each attribute is either
from the left, and hence the name L-attributed.
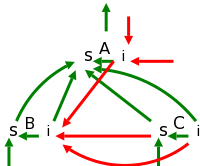
Case three must be handled specially whenever it occurs. The top picture to the right illustrates what the first two cases look like and suggest why there cannot be any cycles. The picture below it corresponds to a fictitious R-attributed definition. One reason L-attributed definitions are favored over R, is the left to right ordering in English. See the example below on type declarations and also consider the grammars that result from left recursion.
The picture shows
that there is an evaluation order for
L-attributed definitions (again assuming no case 3).
More formally, do a depth first traversal of the tree and evaluate
attributes on the way down and on the way up (the first and last
visit by an Euler-tour traversal).
The first time you visit a node (on the way down), evaluate its
inherited attributes.
The second time you visit a node (on the way back up), you evaluate
the synthesized attributes.
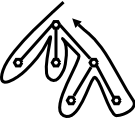
The key point is that all attributes needed will have already been evaluated. Consider the rightmost child of the root in the diagram on the right.
Homework: 3(a-c).