Operating Systems
================ Start Lecture #6 ================
3.1.2: Resource Acquisition
Simple example of the trouble you can get into.
-
Two resources and two processes.
-
Each process wants both resources.
-
Use a semaphore for each. Call them S and T.
-
If both processes execute P(S); P(T); --- V(T); V(S)
all is well.
-
But if one executes instead P(T); P(S); -- V(S); V(T)
disaster! This was the printer/tape example just above.
Recall from the semaphore/critical-section treatment last
chapter, that it is easy to cause trouble if a process dies or stays
forever inside its critical section; we assume processes do not do
this.
Similarly, we assume that no process retains a resource forever.
It may obtain the resource an unbounded number of times (i.e. it can
have a loop forever with a resource request inside), but each time it
gets the resource, it must release it eventually.
3.2: Introduction to Deadlocks
To repeat: A deadlock occurs when a every member of a set of
processes is waiting for an event that can only be caused
by a member of the set.
Often the event waited for is the release of
a resource.
3.2.1: (Necessary) Conditions for Deadlock
The following four conditions (Coffman; Havender) are
necessary but not sufficient for deadlock. Repeat:
They are not sufficient.
-
Mutual exclusion: A resource can be assigned to at most one
process at a time (no sharing).
-
Hold and wait: A processing holding a resource is permitted to
request another.
-
No preemption: A process must release its resources; they cannot
be taken away.
-
Circular wait: There must be a chain of processes such that each
member of the chain is waiting for a resource held by the next member
of the chain.
The first three are characteristics of the system and resources.
That is, for a given system with a fixed set of resources, the first
three conditions are either true or false: They don't change with time.
The truth or falsehood of the last condition does indeed change with
time as the resources are requested/allocated/released.

3.2.2: Deadlock Modeling
On the right are several examples of a
Resource Allocation Graph, also called a
Reusable Resource Graph.
-
The processes are circles.
-
The resources are squares.
-
An arc (directed line) from a process P to a resource R signifies
that process P has requested (but not yet been allocated) resource R.
-
An arc from a resource R to a process P indicates that process P
has been allocated resource R.
Homework: 5.
Consider two concurrent processes P1 and P2 whose programs are.
P1: request R1 P2: request R2
request R2 request R1
release R2 release R1
release R1 release R2
On the board draw the resource allocation graph for various possible
executions of the processes, indicating when deadlock occurs and when
deadlock is no longer avoidable.
There are four strategies used for dealing with deadlocks.
-
Ignore the problem
-
Detect deadlocks and recover from them
-
Avoid deadlocks by carefully deciding when to allocate resources.
-
Prevent deadlocks by violating one of the 4 necessary conditions.
3.3: Ignoring the problem--The Ostrich Algorithm
The “put your head in the sand approach”.
-
If the likelihood of a deadlock is sufficiently small and the cost
of avoiding a deadlock is sufficiently high it might be better to
ignore the problem. For example if each PC deadlocks once per 100
years, the one reboot may be less painful that the restrictions needed
to prevent it.
-
Clearly not a good philosophy for nuclear missile launchers.
-
For embedded systems (e.g., missile launchers) the programs run
are fixed in advance so many of the questions Tanenbaum raises (such
as many processes wanting to fork at the same time) don't occur.
3.4: Detecting Deadlocks and Recovering From Them
3.4.1: Detecting Deadlocks with Single Unit Resources
Consider the case in which there is only one
instance of each resource.
-
Thus a request can be satisfied by only one specific resource.
-
In this case the 4 necessary conditions for
deadlock are also sufficient.
-
Remember we are making an assumption (single unit resources) that
is often invalid. For example, many systems have several printers and
a request is given for “a printer” not a specific printer.
Similarly, one can have many tape drives.
-
So the problem comes down to finding a directed cycle in the resource
allocation graph. Why?
Answer: Because the other three conditions are either satisfied by the
system we are studying or are not in which case deadlock is not a
question. That is, conditions 1,2,3 are conditions on the system in
general not on what is happening right now.
To find a directed cycle in a directed graph is not hard. The
algorithm is in the book. The idea is simple.
-
For each node in the graph do a depth first traversal to see if the
graph is a DAG (directed acyclic graph), building a list as you go
down the DAG (and pruning it as you backtrack back up).
-
If you ever find the same node twice on your list, you have found
a directed cycle, the graph is not a DAG, and deadlock exists among
the processes in your current list.
-
If you never find the same node twice, the graph is a DAG and no
deadlock occurs.
-
The searches are finite since there are a finite number of nodes.
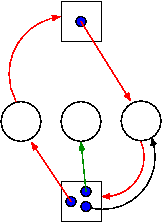
3.4.2: Detecting Deadlocks with Multiple Unit Resources
This is more difficult.
-
The figure on the right shows a resource allocation graph with
multiple unit resources.
-
Each unit is represented by a dot in the box.
-
Request edges are drawn to the box since they represent a request
for any dot in the box.
-
Allocation edges are drawn from the dot to represent that this
unit of the resource has been assigned (but all units of a resource
are equivalent and the choice of which one to assign is arbitrary).
-
Note that there is a directed cycle in red, but there is no
deadlock. Indeed the middle process might finish, erasing the green
arc and permitting the blue dot to satisfy the rightmost process.
-
The book gives an algorithm for detecting deadlocks in this more
general setting. The idea is as follows.
- look for a process that might be able to terminate (i.e., all
its request arcs can be satisfied).
- If one is found pretend that it does terminate (erase all its
arcs), and repeat step 1.
- If any processes remain, they are deadlocked.
-
We will soon do in detail an algorithm (the Banker's algorithm) that
has some of this flavor.
-
The algorithm just given makes the most optimistic assumption
about a running process: it will return all its resources and
terminate normally.
If we still find processes that remain blocked, they are
deadlocked.
-
In the bankers algorithm we make the most pessimistic
assumption about a running process: it immediately asks for all
the resources it can (details later on “can”).
If, even with such demanding processes, the resource manager can
assure that all process terminates, then we can assure that
deadlock is avoided.
3.4.3: Recovery from deadlock
Preemption
Perhaps you can temporarily preempt a resource from a process. Not
likely.
Rollback
Database (and other) systems take periodic checkpoints. If the
system does take checkpoints, one can roll back to a checkpoint
whenever a deadlock is detected. Somehow must guarantee forward
progress.
Kill processes
Can always be done but might be painful. For example some
processes have had effects that can't be simply undone. Print, launch
a missile, etc.
Remark:
We are doing 3.6 before 3.5 since 3.6 is easier.
3.6: Deadlock Prevention
Attack one of the coffman/havender conditions
3.6.1: Attacking Mutual Exclusion
Idea is to use spooling instead of mutual exclusion. Not
possible for many kinds of resources
3.6.2: Attacking Hold and Wait
Require each processes to request all resources at the beginning
of the run. This is often called One Shot.
3.6.3: Attacking No Preempt
Normally not possible.
That is, some resources are inherently preemptable (e.g., memory).
For those deadlock is not an issue.
Other resources are non-preemptable, such as a robot arm.
It is normally not possible to find a way to preempt one of these
latter resources.
3.6.4: Attacking Circular Wait
Establish a fixed ordering of the resources and require that they
be requested in this order. So if a process holds resources #34 and
#54, it can request only resources #55 and higher.
It is easy to see that a cycle is no longer possible.
Homework: 7.
3.5: Deadlock Avoidance
Let's see if we can tiptoe through the tulips and avoid deadlock
states even though our system does permit all four of the necessary
conditions for deadlock.
An optimistic resource manager is one that grants every
request as soon as it can. To avoid deadlocks with all four
conditions present, the manager must be smart not optimistic.
3.5.1 Resource Trajectories
We plot progress of each process along an axis.
In the example we show, there are two processes, hence two axes, i.e.,
planar.
This procedure assumes that we know the entire request and release
pattern of the processes in advance so it is not a practical
solution.
I present it as it is some motivation for the practical solution that
follows, the Banker's Algorithm.
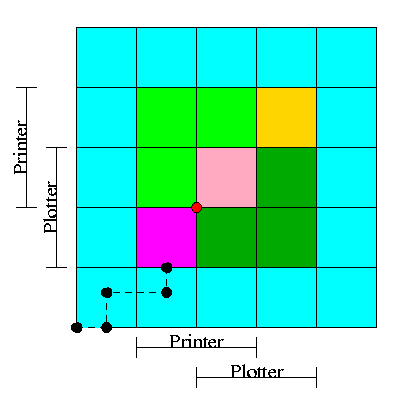
-
We have two processes H (horizontal) and V.
-
The origin represents them both starting.
-
Their combined state is a point on the graph.
-
The parts where the printer and plotter are needed by each process
are indicated.
-
The dark green is where both processes have the plotter and hence
execution cannot reach this point.
-
Light green represents both having the printer; also impossible.
-
Pink is both having both printer and plotter; impossible.
-
Gold is possible (H has plotter, V has printer), but the system
can't get there.
-
The upper right corner is the goal; both processes have finished.
-
The red dot is ... (cymbals) deadlock. We don't want to go there.
-
The cyan is safe. From anywhere in the cyan we have horizontal
and vertical moves to the finish point (the upper right corner)
without hitting any impossible area.
-
The magenta interior is very interesting. It is
- Possible: each processor has a different resource
- Not deadlocked: each processor can move within the magenta
- Deadly: deadlock is unavoidable. You will hit a magenta-green
boundary and then will no choice but to turn and go to the red dot.
-
The cyan-magenta border is the danger zone.
-
The dashed line represents a possible execution pattern.
-
With a uniprocessor no diagonals are possible. We either move to
the right meaning H is executing or move up indicating V is executing.
-
The trajectory shown represents.
- H excuting a little.
- V excuting a little.
- H executes; requests the printer; gets it; executes some more.
- V executes; requests the plotter.
-
The crisis is at hand!
-
If the resource manager gives V the plotter, the magenta has been
entered and all is lost. “Abandon all hope ye who enter
here” --Dante.
-
The right thing to do is to deny the request, let H execute moving
horizontally under the magenta and dark green. At the end of the dark
green, no danger remains, both processes will complete successfully.
Victory!
-
This procedure is not practical for a general purpose OS since it
requires knowing the programs in advance. That is, the resource
manager, knows in advance what requests each process will make and in
what order.
Homework: 10, 11, 12.
3.5.2: Safe States
Avoiding deadlocks given some extra knowledge.
-
Not surprisingly, the resource manager knows how many units of each
resource it had to begin with.
-
Also it knows how many units of each resource it has given to
each process.
-
It would be great to see all the programs in advance and thus know
all future requests, but that is asking for too much.
-
Instead, when each process starts, it announces its maximum usage.
That is each process, before making any resource requests, tells
the resource manager the maximum number of units of each resource
the process can possible need.
This is called the claim of the process.
-
If the claim is greater than the total number of units in the
system the resource manager kills the process when receiving
the claim (or returns an error code so that the process can
make a new claim).
-
If during the run the process asks for more than its claim,
the process is aborted (or an error code is returned and no
resources are allocated).
-
If a process claims more than it needs, the result is that the
resource manager will be more conservative than need be and there
will be more waiting.
Definition: A state is safe
if there is an ordering of the processes such that: if the
processes are run in this order, they will all terminate (assuming
none exceeds its claim).
Recall the comparison made above between detecting deadlocks (with
multi-unit resources) and the banker's algorithm
-
The deadlock detection algorithm given makes the most
optimistic assumption
about a running process: it will return all its resources and
terminate normally.
If we still find processes that remain blocked, they are
deadlocked.
-
The banker's algorithm makes the most pessimistic
assumption about a running process: it immediately asks for all
the resources it can (details later on “can”).
If, even with such demanding processes, the resource manager can
assure that all process terminates, then we can assure that
deadlock is avoided.
In the definition of a safe state no assumption is made about the
running processes; that is, for a state to be safe termination must
occur no matter what the processes do (providing the all terminate and
to not exceed their claims).
Making no assumption is the same as making the most pessimistic
assumption.
Give an example of each of the four possibilities. A state that is
-
Safe and deadlocked--not possible.
-
Safe and not deadlocked--trivial (e.g., no arcs).
-
Not safe and deadlocked--easy (any deadlocked state).
-
Not safe and not deadlocked--interesting.
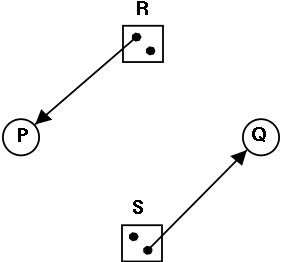 Is the figure on the right safe or not?
Is the figure on the right safe or not?
-
You can NOT tell until I give you the initial claims of the
process.
-
Please do not make the unfortunately common exam mistake to give
an example involving safe states without giving the claims.
-
For the figure on the right, if the initial claims are:
P: 1 unit of R and 2 units of S (written (1,2))
Q: 2 units of R and 1 units of S (written (2,1))
the state is NOT safe.
-
But if the initial claims are instead:
P: 2 units of R and 1 units of S (written (2,1))
Q: 1 unit of R and 2 units of S (written (1,2))
the state IS safe.
-
Explain why this is so.
A manager can determine if a state is safe.
-
Since the manager know all the claims, it can determine the maximum
amount of additional resources each process can request.
-
The manager knows how many units of each resource it has left.
The manager then follows the following procedure, which is part of
Banker's Algorithms discovered by Dijkstra, to
determine if the state is safe.
-
If there are no processes remaining, the state is
safe.
-
Seek a process P whose max additional requests is less than
what remains (for each resource type).
-
If no such process can be found, then the state is
not safe.
-
The banker (manager) knows that if it refuses all requests
excepts those from P, then it will be able to satisfy all
of P's requests. Why?
Ans: Look at how P was chosen.
-
The banker now pretends that P has terminated (since the banker
knows that it can guarantee this will happen). Hence the banker
pretends that all of P's currently held resources are returned. This
makes the banker richer and hence perhaps a process that was not
eligible to be chosen as P previously, can now be chosen.
-
Repeat these steps.
Example 1
A safe state with 22 units of one resource
| process | initial claim | current alloc | max add'l |
|---|
| X | 3 | 1 | 2 |
| Y | 11 | 5 | 6 |
| Z | 19 | 10 | 9 |
| Total | 16 |
| Available | 6 |
-
One resource type R with 22 unit
-
Three processes X, Y, and Z with initial claims 3, 11, and 19
respectively.
-
Currently the processes have 1, 5, and 10 units respectively.
-
Hence the manager currently has 6 units left.
-
Also note that the max additional needs for the processes are 2,
6, 9 respectively.
-
So the manager cannot assure (with its current
remaining supply of 6 units) that Z can terminate. But that is
not the question.
-
This state is safe
-
Use 2 units to satisfy X; now the manager has 7 units.
-
Use 6 units to satisfy Y; now the manager has 12 units.
-
Use 9 units to satisfy Z; done!
Example 2
An unsafe state with 22 units of one resource
| process | initial claim | current alloc | max add'l |
|---|
| X | 3 | 1 | 2 |
| Y | 11 | 5 | 6 |
| Z | 19 | 12 | 7 |
| Total | 18 |
| Available | 4 |
Start with example 1 and assume that Z now requests 2 units and the
manager grants them.
-
Currently the processes have 1, 5, and 12 units respectively.
-
The manager has 4 units.
-
The max additional needs are 2, 6, and 7.
-
This state is unsafe
-
Use 2 unit to satisfy X; now the manager has 5 units.
-
Y needs 6 and Z needs 7 so we can't guarantee satisfying either
-
Note that we were able to find a process that can terminate (X)
but then we were stuck. So it is not enough to find one process.
We must find a sequence of all the processes.




 Is the figure on the right safe or not?
Is the figure on the right safe or not?