Operating Systems

Remark: A very small change was made to lab2 (on the mailing list thurs evening). The name of the random number file must be random-numbers. The first sentence of the last paragraph on page 1 now states.

The function randomOS(U) reads a random non-negative integer X from a file named random-numbers (in the current directory) and returns the value 1+(X mod U).

Variants of Round Robin

• State dependent RR
  • Same as RR but q is varied dynamically depending on the state of the system.
  • Favor processes holding important resources.
    • For example, non-swappable memory.
    • Perhaps this should be considered medium term scheduling since you probably do not recalculate q each time.
• External priorities: RR but a user can pay more and get bigger q. That is one process can be given a higher priority than another. But this is not an absolute priority: the lower priority (i.e., less important) process does get to run, but not as much as the higher priority process.

Priority Scheduling

Each job is assigned a priority (externally, perhaps by charging more for higher priority) and the highest priority ready job is run.

• Similar to “External priorities” above
• If many processes have the highest priority, use RR among them.
• Can easily starve processes (see aging below for fix).
• Can have the priorities changed dynamically to favor processes holding important resources (similar to state dependent RR).
• Many policies can be thought of as priority scheduling in which we run the job with the highest priority (with different notions of priority for different policies). For example, FIFO and RR are priority scheduling where the priority is the time spent on the ready list/queue.

Priority aging

As a job is waiting, raise its priority so eventually it will have the maximum priority.

• This prevents starvation (assuming all jobs terminate or the policy is preemptive).
• Starvation means that some process is never run, because it never has the highest priority. It is also starvation, if process A runs for a while, but then is never able to run again, even though it is ready. The formal way to say this is “No job can remain in the ready state forever”.
• There may be many processes with the maximum priority.
• If so, can use FIFO among those with max priority (risks starvation if a job doesn't terminate) or can use RR.
• Can apply priority aging to many policies, in particular to priority scheduling described above.

Selfish RR (SRR, **, SRR, **)

• Preemptive.
• Perhaps it should be called “snobbish RR”.
• “Accepted processes” run RR.
• Accepted process have their priority increase at rate b≥0.
• A new process starts at priority 0; its priority increases at rate a≥0.
• A new process becomes an accepted process when its priority reaches that of an accepted process (or when there are no accepted processes).
• Once a process is accepted it remains accepted until it terminates.
• Note that at any time all accepted processes have same priority.
• It is not clear what is supposed to happen when a process blocks. Should it priority get reset and have unblock act like create? Should the priority continue to grow (at rate a or b)? Should its priority be frozen during the blockage. Let us assume the second case (continue to grow since it seems the simplest).
• If b≥a, get FCFS.
• If b=0, get RR.
• If a>b>0, it is interesting.
• If b>a=0, you get RR in "batches". This is similar to n-step scan for disk I/O.

Shortest Job First (SPN, SJF, SJF, SJF)

Sort jobs by total execution time needed and run the shortest first.

• Nonpreemptive
• First consider a static situation where all jobs are available in the beginning and we know how long each one takes to run. For simplicity lets consider “run-to-completion”, also called “uniprogrammed” (i.e., we don't even switch to another process on I/O). In this situation, uniprogrammed SJF has the shortest average waiting time.
  • Assume you have a schedule with a long job right before a short job.
  • Consider swapping the two jobs.
  • This decreases the wait for the short by the length of the long job and increases the wait of the long job by the length of the short job.
  • This decreases the total waiting time for these two.
  • Hence decreases the total waiting for all jobs and hence decreases the average waiting time as well.
  • Hence, whenever a long job is right before a short job, we can swap them and decrease the average waiting time.
  • Thus the lowest average waiting time occurs when there are no short jobs right before long jobs.
  • This is uniprogrammed SJF.
• The above argument illustrates an advantage of favoring short jobs (e.g., RR with small quantum): the average waiting time is reduced.
• In the more realistic case of true SJF where the scheduler switches to a new process when the currently running process blocks (say for I/O), we should call the policy shortest next-CPU-burst first.
• The difficulty is predicting the future (i.e., knowing in advance the time required for the job or next-CPU-burst).
• This is an example of priority scheduling.

Homework: 39, 40. Note that when the book says RR with each process getting its fair share, it means Processor Sharing.

Preemptive Shortest Job First (PSPN, SRT, PSJF/SRTF, --)

Preemptive version of above

• Permit a process that enters the ready list to preempt the running process if the time for the new process (or for its next burst) is less than the remaining time for the running process (or for its current burst).
• It will never happen that a process in the ready list will require less time than the remaining time for the currently running process. Why?
  Ans: When the process joined the ready list it would have started running if the current process had more time remaining. Since that didn't happen the current job had less time remaining and now it has even less.
• Can starve a process that require a long burst.
  • This is fixed by the standard technique.
  • What is that technique?
    Ans: Priority aging.
• Another example of priority scheduling.
• Consider three processes all starting at time 0. One requires 1ms, the second 100ms, the third 10sec (seconds). Compute the total/average waiting time and compare to RR q=1ms, FCFS, and PS.

Highest Penalty Ratio Next (HPRN, HRN, **, **)

Run the process that has been “hurt” the most.

• For each process, let r = T/t; where T is the wall clock time this process has been in system and t is the running time of the process to date.
• If r=2.5, that means the job has been running 1/2.5 = 40% of the time it has been in the system.
• We call r the penalty ratio and run the process having the highest r value.
• We must worry about a process that just enters the system since t=0 and hence the ratio is undefined. Define t to be the max of 1 and the running time to date. Since now t is at least 1, the ratio is always defined.
• HPRN is normally defined to be non-preemptive (i.e., the system only checks r when a burst ends), but there is an preemptive analogue
  • When putting process into the run state compute the time at which it will no longer have the highest ratio and set a timer.
  • When a process is moved into the ready state, compute its ratio and preempt if needed.
• HRN stands for highest response ratio next and means the same thing.
• This policy is yet another example of priority scheduling

Remark: Recall that SFJ/PSFJ do a good job of minimizing the average waiting time. The problem with them is the difficulty in finding the job whose next CPU burst is minimal. We now learn two scheduling algorithms that attempt to do this (approximately). The first one does this statically, presumably with some manual help; the second is dynamic and fully automatic.

Multilevel Queues (**, **, MLQ, **)

Put different classes of processs in different queues

• Processs do not move from one queue to another.
• Can have different policies on the different queues.
  For example, might have a background (batch) queue that is FCFS and one or more foreground queues that are RR.
• Must also have a policy among the queues.
  For example, might have two queues, foreground and background, and give the first absolute priority over the second
  • Might apply aging to prevent background starvation.
  • But might not, i.e., no guarantee of service for background processes. View a background process as a “cycle soaker”.
  • Might have 3 queues, foreground, background, cycle soaker.

Multilevel Feedback Queues (FB, MFQ, MLFBQ, MQ)

As with multilevel queues above we have many queues, but now processs move from queue to queue in an attempt to dynamically separate “batch-like” from interactive processs so that we can favor the latter.

• Remember that average waiting time is achieved by SJF, and this is an attempt to determine dynamically those processes that are interactive, which means have a very short cpu burst.
• Run processs from the highest priority nonempty queue in a RR manner.
• When a process uses its full quanta (looks a like batch process), move it to a lower priority queue.
• When a process doesn't use a full quanta (looks like an interactive process), move it to a higher priority queue.
• A long process with frequent (perhaps spurious) I/O will remain in the upper queues.
• Might have the bottom queue FCFS.
• Many variants.
  For example, might let process stay in top queue 1 quantum, next queue 2 quanta, next queue 4 quanta (i.e., sometimes return a process to the rear of the same queue it was in if the quantum expires).

Theoretical Issues

Considerable theory has been developed.

• NP completeness results abound.
• Much work in queuing theory to predict performance.
• Not covered in this course.

Medium-Term Scheduling

In addition to the short-term scheduling we have discussed, we add medium-term scheduling in which decisions are made at a coarser time scale.

• Called memory scheduling by Tanenbaum (part of his three level scheduling).
• Suspend (swap out) some process if memory is over-committed.
• Criteria for choosing a victim.
  • How long since previously suspended.
  • How much CPU time used recently.
  • How much memory does it use.
  • External priority (pay more, get swapped out less).
• We will discuss medium term scheduling again when we study memory management.

Long Term Scheduling

• “Job scheduling”. Decide when to start jobs, i.e., do not necessarily start them when submitted.
• Force user to log out and/or block logins if over-committed.
  • CTSS (an early time sharing system at MIT) did this to insure decent interactive response time.
  • Unix does this if out of processes (i.e., out of PTEs).
  • “LEM jobs during the day” (Grumman).
• Called admission scheduling by Tanenbaum (part of three level scheduling).
• Many supercomputer sites.

2.5.4: Scheduling in Real Time Systems

Skipped

2.5.5: Policy versus Mechanism

Skipped.

2.5.6: Thread Scheduling

Skipped.

Research on Processes and Threads

Skipped.

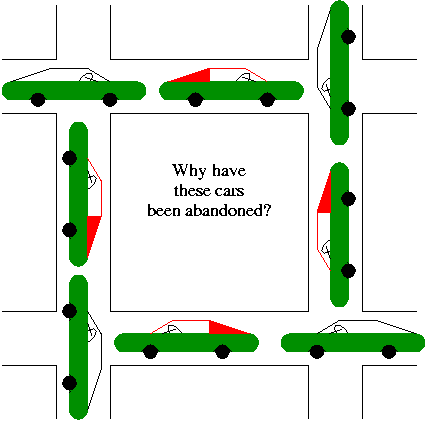
Chapter 3: Deadlocks

A deadlock occurs when every member of a set of processes is waiting for an event that can only be caused by a member of the set.

Often the event waited for is the release of a resource.

In the automotive world deadlocks are called gridlocks.

• The processes are the cars.
• The resources are the spaces occupied by the cars

Old Reward: I used to give one point extra credit on the final exam for anyone who brings a real (e.g., newspaper) picture of an automotive deadlock. Note that it must really be a gridlock, i.e., motion is not possible without breaking the traffic rules. A huge traffic jam is not sufficient. This was solved last semester so no reward any more. One of the winners in on my office door.

For a computer science example consider two processes A and B that each want to print a file currently on tape.

1. A has obtained ownership of the printer and will release it after printing one file.
2. B has obtained ownership of the tape drive and will release it after reading one file.
3. A tries to get ownership of the tape drive, but is told to wait for B to release it.
4. B tries to get ownership of the printer, but is told to wait for A to release the printer.

Bingo: deadlock!

3.1: Resources

The resource is the object granted to a process.

3.1.1: Preemptable and Nonpreemptable Resources

• Resources come in two types
  1. Preemptable, meaning that the resource can be taken away from its current owner (and given back later). An example is memory.
  2. Non-preemptable, meaning that the resource cannot be taken away. An example is a printer.
• The interesting issues arise with non-preemptable resources so those are the ones we study.
• Life history of a resource is a sequence of
  1. Request
  2. Allocate
  3. Use
  4. Release
• Processes make requests, use the resource, and release the resource. The allocate decisions are made by the system and we will study policies used to make these decisions.