
We are not covering global flow analysis; it is a key component of optimization and would be a natural topic in a follow-on course. Nonetheless there is something we can say just by examining the flow graphs we have constructed. For this discussion I am ignoring tricky and important issues concerning arrays and pointer references (specifically, disambiguation). You may wish to assume that the program contains no arrays or pointers for these comments.
We have seen that a simple backwards scan of the statements in a
basic block enables us to determine the variables that are
live-on-entry and those that are dead-on-entry.
Those variables that do not occur in the block are in neither
category; perhaps we should call them ignored by the block
.
We shall see below that it would be lovely to know which variables are live/dead-on-exit. This means which variables hold values at the end of the block that will / will not be used. To determine the status of v on exit of a block B, we need to trace all possible execution paths beginning at the end of B. If all these paths reach a block where v is dead-on-entry before they reach a block where v is live-on-entry, then v is dead on exit for block B.
The goal is to obtain a visual picture of how information flows through the block. The leaves will show the values entering the block and as we proceed up the DAG we encounter uses of these values defs (and redefs) of values and uses of the new values.
Formally, this is defined as follows.
live on exit, an officially-mysterious term meaning values possibly used in another block. (Determining the live on exit values requires global, i.e., inter-block, flow analysis.)
As we shall see in the next few sections various basic-block
optimizations are facilitated by using the DAG.

As we create nodes for each statement, proceeding in the static order of the statements, we might notice that a new node is just like one already in the DAG in which case we don't need a new node and can use the old node to compute the new value in addition to the one it already was computing.
Specifically, we do not construct a new node if an existing node has the same children in the same order and is labeled with the same operation.
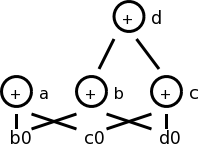
Consider computing the DAG for the following block of code.
a = b + c
c = a + x
d = b + c
b = a + x
The DAG construction is explain as follows (the movie on the right accompanies the explanation).
You might think that with only three computation nodes in the DAG,
the block could be reduced to three statements (dropping the
computation of b).
However, this is wrong.
Only if b is dead on exit can we omit the computation of b.
We can, however, replace the last statement with the simpler
b = c.
Sometimes a combination of techniques finds improvements that no
single technique would find.
For example if a-b is computed, then both a and b are incremented by
one, and then a-b is computed again, it will not be recognized as a
common subexpression even though the value has not changed.
However, when combined with various algebraic transformations, the
common value can be recognized.
Assume we are told (by global flow analysis) that certain values are dead on exit. We examine each root (node with no ancestor) and delete any that have no live variables attached. This process is repeated since new roots may have appeared.
For example, if we are told, for the picture on the right, that only a and b are live, then the root d can be removed since d is dead. Then the rightmost node becomes a root, which also can be removed (since c is dead).
Some of these are quite clear. We can of course replace x+0 or 0+x by simply x. Similar considerations apply to 1*x, x*1, x-0, and x/1.
Another class of simplifications is strength reduction, where we replace one operation by a cheaper one. A simple example is replacing 2*x by x+x on architectures where addition is cheaper than multiplication.
A more sophisticated strength reduction is applied by compilers that
recognize induction variables
(loop indices).
Inside a
for i from 1 to N
loop, the expression 4*i can be strength reduced to j=j+4 and 2^i
can be strength reduced to j=2*j (with suitable initializations of j
just before the loop).
Other uses of algebraic identities are possible; many require a
careful reading of the language reference manual to ensure their
legality.
For example, even though it might be advantageous to convert
((a + b) * f(x)) * a
to
((a + b) * a) * f(x)
it is illegal in Fortran since the programmer's use of parentheses
to specify the order of operations can not be violated.
Does
a = b + c
x = y + c + b + r
contain a common subexpression of b+c that need be evaluated only
once?Arrays are tricky. Question: Does
x = a[i]
a[j] = 3
z = a[i]
contain a common subexpression of a[i] that need be evaluated only
once?A statement of the form x = a[i] generates a node labeled with the operator =[] and the variable x, and having children a0, the initial value of a, and the value of i.
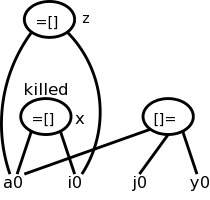
A statement of the form a[j] = y generates a node labeled with operator []= and three children a0. j, and y, but with no variable as label. The new feature is that this node kills all existing nodes depending on a0. A killed node can not received any future labels so cannot becomew a common subexpression.
Returning to our example
x = a[i]
a[j] = 3
z = a[i]
We obtain the top figure to the right.
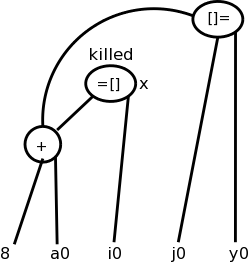
Sometimes it is not children but grandchildren (or other descendant) that are arrays. For example we might have
b = a + 8 // b[i] is 8 bytes past a[i]
x = b[i]
b[j] = y
Again we need to have the third statement kill the second node even
though it is caused by a grandchild.
This is shown in the bottom figure.
Pointers are even trickier than arrays.
Together they have spawned a mini-industry in disambiguation
,
i.e., when can we tell whether two array or pointer references refer
to the same or different locations.
A trivial case of disambiguation occurs with.
p = &x
*p = y
In this case we know precisely the value of p so the second
statement kills only nodes with x attached.
With no disambiguation information, we must assume that a pointer can refer to any location. Consider
x = *p
*q = y
We must treat the first statement as a use of every variable; pictorially the =* operator takes all current nodes with identifiers as arguments. This impacts dead code elimination.
We must treat the second statement as writing every variable. That is all existing nodes are killed, which impacts common subexpression elimination.
In our basic-block level approach, a procedure call has properties similar to a pointer reference: For all x in the scope of P, we must treat a call of P as using all nodes with x attached and also kills those same nodes.
Now that we have improved the DAG for a basic block, we need to regenerate the quads. That is, we need to obtain the sequence of quads corresponding to the new DAG.
We need to construct a quad for every node that has a variable attached. If there are several variables attached we chose a live-on-exit variable, assuming we have done the necessary global flow analysis to determine such variables).
If there are several live-on-exit variables we need to compute one and make a copy so that we have both. An optimization pass may eliminate the copy if it is able to assure that one such variable may be used whenever the other is referenced.
Recall the example from our movie
a = b + c
c = a + x
d = b + c
b = a + x
If b is dead on exit, the first three instructions suffice. If not we produce instead
a = b + c
c = a + x
d = b + c
b = c
which is still an improvement as the copy instruction is less
expensive than the addition on most architectures.
If global analysis shows that, whenever this definition of b is used, c contains the same value, we can eliminate the copy and use c in place of b.
Note that of the following 5, rules 2 are due to arrays, and 2 due to pointers.
Homework: 9.14,
9.15 (just simplify the 3-address code of 9.14 using the two cases
given in 9.15), and
9.17 (just construct the DAG for the given basic block in the two
cases given).
A big issue is proper use of the registers, which are often in short supply, and which are used/required for several purposes.
For this section we assume a RISC architecture. Specifically, we assume only loads and stores touch memory; that is, the instruction set consists of
LD reg, mem
ST mem, reg
OP reg, reg, reg
where there is one OP for each operation type used in the three
address code.
The 1e uses CISC like instructions (2 operands). Perhaps 2e switched to RISC in part due to the success of the ROPs in the Pentium Pro.
A major simplification is we assume that, for each three address operation, there is precisely one machine instruction that accomplishes the task. This eliminates the question of instruction selection.
We do, however, consider register usage. Although we have not done global flow analysis (part of optimization), we will point out places where live-on-exit information would help us make better use of the available registers.
Recall that the mem operand in the load LD and store ST
instructions can use any of the previously discussed addressing
modes.
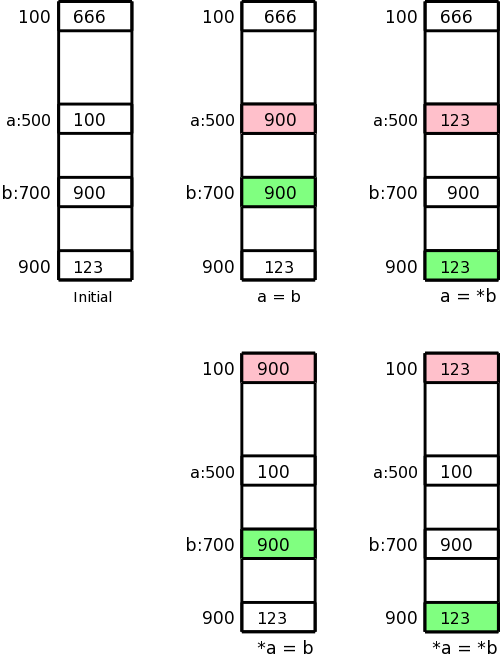
Remember that in 3-address instructions, the variables written are addresses, i.e., they represent l-values.
Let us assume a is 500 and b is 700, i.e., a and b refer to locations 500 and 700 respectively. Assume further that location 100 contains 666, location 500 contains 100, location 700 contains 900, and location 900 contains 123. This initial state is shown in the upper left picture.
In the four other pictures the contents of the pink location has been changed to the contents of the light green location. These correspond to the three-address assignment statements shown below each picture. The machine instructions indicated below implement each of these assignment statements.
a = b
LD R1, b
ST a, R1
a = *b
LD R1, b
LD R1, 0(R1)
ST a, R1
*a = b
LD R1, b
LD R2, a
ST 0(R2), R1
*a = *b
LD R1, b
LD R1, 0(R1)
LD R2, a
ST 0(R2), R1
These are the primary data structures used by the code generator. They keep track of what values are in each register as well as where a given value resides.
The register descriptor could be omitted since you can compute it from the address descriptors.
There are basically three parts to (this simple algorithm for) code generation.
We will isolate register allocation in a function getReg(Instruction), which is presented later. First presented is the algorithm to generate instructions. This algorithm uses getReg() and the descriptors. Then we learn how to manage the descriptors and finally we study getReg() itself.
Given a quad OP x, y, z (i.e., x = y OP z), proceed as follows.
Call getReg(OP x, y, z) to get Rx, Ry, and Rz, the registers to be used for x, y, and z respectively.
Note that getReg merely selects the registers, it does not guarantee that the desired values are present in these registers.
Check the register descriptor for Ry.
If y is not present in Ry, check the address descriptor
for y and issue
LD Ry, y
The 2e uses y' (not y) as source of the load, where y' is some location containing y (1e suggests this as well). I don't see how the value of y can appear in any memory location other than y. Please check me on this.
One might worry that either
It would be a serious bug in the algorithm if the first were
true, and I am confident it is not.
The second might be a possible design, but when we study
getReg(), we will see that if the value of y is in some
register, then the chosen Ry will contain that
value.
When processing
x = y
steps 1 and 2 are the same as above
(getReg() will set Rx=Ry).
Step 3 is vacuous and step 4 is omitted.
This says that if y was already in a register before the copy
instruction, no code is generated at this point.
Since the value of y is not in its memory location,
we may need to store this value back into y at block exit.
You probably noticed that we have not yet generated any store instructions; They occur here (and during spill code in getReg()). We need to ensure that all variables needed by (dynamically) subsequent blocks (i.e., those live-on-exit) have their current values in their memory locations.
All live on exit variables (for us all non-temporaries) need to be in their memory location on exit from the block.
Check the address descriptor for each live on exit variable.
If its own memory location is not listed, generate
ST x, R
where R is a register listed in the address descriptor
This is fairly clear. We just have to think through what happens when we do a load, a store, an OP, or a copy. For R a register, let Desc(R) be its register descriptor. For x a program variable, let Desc(x) be its address descriptor.
Since we haven't specified getReg() yet, we will assume there are an unlimited number of registers so we do not need to generate any spill code (saving the register's value in memory). One of getReg()'s jobs is to generate spill code when a register needs to be used for another purpose and the current value is not presently in memory.
Despite having ample registers and thus not generating spill code, we will not be wasteful of registers.
This example is from the book. I give another example after presenting getReg(), that I believe justifies my claim that the book is missing an action, as indicated above.
Assume a, b, c, and d are program variables and t, u, v are compiler generated temporaries (I would call these t$1, t$2, and t$3). The intermediate language program is on the left with the generated code for each quad shown. To the right is shown the contents of all the descriptors. The code generation is explained below the diagram.

t = a - b
LD R1, a
LD R2, b
SUB R2, R1, R2
u = a - c
LD r3, c
SUB R1, R1, R3
v = t + u
ADD R3, R2, R1
a = d
LD R2, d
d = v + u
ADD R1, R3, R1
exit
ST a, R2
ST d, R1
What follows describes the choices made. Confirm that the values in the descriptors matches the explanations.
Consider
x = y OP z
Picking registers for y and z are the same; we just do y.
Choosing a register for x is a little different.
A copy instruction
x = y
is easier.
Similar to demand paging, where the goal is to produce an available frame, our objective here is to produce an available register we can use for Ry. We apply the following steps in order until one succeeds. (Step 2 is a special case of step 3.)
As stated above choosing Rz is the same as choosing Ry.
Choosing Rx has the following differences.
getReg(x=y) chooses Ry as above and chooses Rx=Ry.
R1 R2 R3 a b c d e
a b c d e
a = b + c
LD R1, b
LD R2, c
ADD R3, R1, R2
R1 R2 R3 a b c d e
b c a R3 b,R1 c,R2 d e
d = a + e
LD R1, e
ADD R2, R3, R1
R1 R2 R3 a b c d e
2e → e d a R3 b,R1 c R2 e,R1
me → e d a R3 b c R2 e,R1
We needed registers for d and e; none were free. getReg() first chose R2 for d since R2's current contents, the value of c, was also located in memory. getReg() then chose R1 for e for the same reason.
Using the 2e algorithm, b might appear to be in R1 (depends if you look in the address or register descriptors).
a = e + d
ADD R3, R1, R2
Descriptors unchanged
e = a + b
ADD R1, R3, R1 ← possible wrong answer from 2e
R1 R2 R3 a b c d e
e d a R3 b,R1 c R2 R1
LD R1, b
ADD R1, R3, R1
R1 R2 R3 a b c d e
e d a R3 b c R2 R1
The 2e might think R1 has b (address descriptor) and also conclude R1 has only e (register descriptor) so might generate the erroneous code shown.
Really b is not in a register so must be loaded. R3 has the value of a so was already chosen for a. R2 or R1 could be chosen. If R2 was chosen, we would need to spill d (we must assume live-on-exit, since we have no global flow analysis). We choose R1 since no spill is needed: the value of e (the current occupant of R1) is also in its memory location.
exit
ST a, R3
ST d, R2
ST e, R1
Skipped.
Skipped.
What if a given quad needs several OPs and we have choices?
We would like to be able to describe the machine OPs in a way that enables us to find a sequence of OPs (and LDs and STs) to do the job.
The idea is that you express the quad as a tree and express each OP
as a (sub-)tree simplification, i.e. the op replaces a subtree by a
simpler subtree.
In fact the simpler subtree is just a single node.
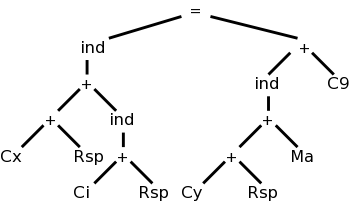
The diagram on the right represents x[i] = y[a] + 9, where x and y are on the stack and a is in the static area. M's are values in memory; C's are constants; and R's are registers. The weird ind (presumably short for indirect) treats its argument as a memory location.
Compare this to grammars: A production replaces the RHS by the LHS. We consider context free grammars where the LHS is a single nonterminal.
For example, a LD replaces a Memory node with a Register node.
Another example is that ADD Ri, Ri, Rj replaces a subtree consisting of a + with both children registers (i and j) with a Register node (i).
As you do the pattern matching and reductions (apply the productions), you emit the corresponding code (semantic actions). So to support a new processor, you need to supply the tree transformations corresponding to every instruction in the instruction set.
This is quite cute.
We assume all operators are binary and label the instruction tree with something like the height. This gives the minimum number of registers needed so that no spill code is required. A few details follow.
biggerchild L regs.
Can see this is optimal (assuming you have enough registers).
Rough idea is to apply the above recursive algorithm, but at each recursive step, if the number of regs is not enough, store the result of the first child computed before starting the second.
Skipped