Skipped.
Remark: As mentioned before 6.6 in the notes is 6.6 in 2e and 8.4 in 1e. However the third level material is not is the same order. In particular this section (6.6.6) is very early in 8.4.
If ther are boolean variables (or variables into which a boolean value can be placed), we can have boolean assignment statements. That is we might evaluate boolean expressions outside of control flow statements.
Recall that the code we generated for boolean expressions (inside control flow statements) used inherited attributes to push down the tree the exit labels B.true and B.false. How are we to deal with Boolean assignment statements?
Up to now we have used the so called jumping code
method for
Boolean quantities.
We evaluated Boolean expressions (in the context of control flow
statements) by using inherited attributes to push down the tree the
true and false exits (i.e., the target locations to jump to if the
expression evaluates to true and false).
With this method if we have a Boolean assignment statement, we just let the true and false exits lead to statements
LHS = true
LHS = false
respectively.
In the second method we simply treat boolean expressions as
expressions.
That is, we just mimic the actions we did for integer/real
evaluations.
Thus Boolean assignment statements like
a = b OR (c AND d AND (x < y))
just work.
For control flow statements like
while (boolean-expression) statement-list end
if (boolean-expression) statement-list else statement-list end
we simply evaluate the boolean expression as if it was part of an
assignment statement and then have two jumps to where we should go
if the result is true or false.
However this is wrong. In C if (a=0 || 1/a > f(a)) is guaranteed not to divide by zero and the above implementation fails to provide this guarantee. We must somehow implement short-circuit boolean evaluation.
Skipped.
Our intermediate code uses symbolic labels.
At some point these must be translated into addresses of
instructions.
If we use quads all instructions are the same length so the address
is just the number of the instruction.
Sometimes we generate the jump before we generate the target so we
can't put in the instruction number on the fly
.
Indeed, that is why we used symbolic labels.
The easiest method of fixing this up is to make an extra pass (or
two) over the quads to determine the correct instruction number and
use that to replace the symbolic label.
This is extra work; a more efficient technique, which is independent
of compilation, is called backpatching
.
Evaluate an expression, compare it with a vector of constants that are viewed as labels of the arms of the switch, and execute the matching arm (or a default).
The C language is unusual in that the various cases are just labels
for a giant computed goto
at the beginning.
The more traditional idea is that you execute just one of the arms,
as in a series of
if
else if
else if
...
end if
else if'sabove. This executes roughly 2k jumps (worst case) for k cases.
The lab 3 grammar does not have a switch statement so we won't do a detailed SDD.
Such an SDD would be organized as follows.
Much of the work for procedures involves storage issues and the run time environment; this is discussed in the next chapter.
In order to support inter-procedural type checking by the compiler, we need to define the called procedure in the calling procedure, which the lab 3 grammar doesn't support except for calling itself recursively. So the best we can do is type check recursive calls.
The basic scheme for type checking recursive (or other calls) is to
generate a table entry for the procedure that contains
its signature
, i.e., the types of its parameters and its
result type.
Recall the SDD
for declarations.
These semantic rules pass up the totalSize to the
ds → d ds
production.
What is needed is for the ps (parameters) to do an analogous thing with their declarations but also (or perhaps instead) pass up a representation of the declarations themselves which when it reaches the top is the signature for a procedure and when put together with the return is the signature for a function.
More serious is supporting nested procedure definitions (defining a procedure inside a procedure). Lab 3 doesn't support this because a procedure or function definition is not a declaration. It would be easy to enhance the grammar to fix this, but the serious work is that then you need nested identifier tables.
Our lexer doesn't support this. So you would remove table building from the lexer and instead do it in the parser and when a new scope (procedure definition, record definition, begin block) arises you push the current tables on a stack and begin a new one. When the nested scope ends, you pop the tables.
Homework: Read Chapter 7.
We are discussing storage organization from the point of view of the compiler, which must allocate space for programs to be run. In particular, we are concerned with only virtual addresses and treat them uniformly.
This should be compared with an operating systems treatment, where we worry about how to effectively map this configuration to real memory. For example see see these two diagrams in my OS class notes, which illustrate an OS difficulty with our allocation method, which uses a very large virtual address range and one solution.
Some system require various alignment constraints. For example 4-byte integers might need to begin at a byte address that is a multiple of four. Unaligned data might be illegal or might lower performance. To achieve proper alignment padding is often used.
expansion region.
new, or via a library function call, such as malloc(). It is deallocated either by another executable statement, such as a call to free(), or automatically by the system.
Much (often most) data cannot be statically allocated. Either its size is not know at compile time or its lifetime is only a subset of the program's execution.
Early versions of Fortran used only statically allocated data. This required that each array had a constant size specified in the program. Another consequence of supporting only static allocation was that recursion was forbidden (otherwise the compiler could not tell how many versions of a variable would be needed).
Modern languages, including newer versions of Fortran, support both static and dynamic allocation of memory.
The advantage supporting dynamic storage allocation is the increased flexibility and storage efficiency possible (instead of declaring an array to have a size adequate for the largest data set; just allocate what is needed). The advantage of static storage allocation is that it avoids the runtime costs for allocation/deallocation and may permit faster code sequences for referencing the data.
An (unfortunately, all too common) error is a so-called memory leak
where a long running program repeated allocates memory that it fails
to delete, even after it can no longer be referenced.
To avoid memory leaks and ease programming, several programming
language systems employ automatic garbage collection
.
That means the runtime system itself can determine if data
can no longer be referenced and if so automatically deallocates it.
Achievements.
Recall the fibonacci sequence 1,1,2,3,5,8, ... defined by f(1)=f(2)=1 and, for n>2, f(n)=f(n-1)+f(n-2). Consider the function calls that result from a main program calling f(5). On the left we show the calls and returns linearly and on the right in tree form. The latter is sometimes called the activation tree or call tree.
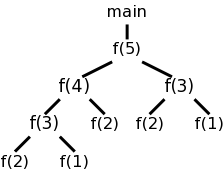
System starts main
enter f(5)
enter f(4)
enter f(3)
enter f(2)
exit f(2)
enter f(1)
exit f(1)
exit f(3)
enter f(2) int a[10];
exit f(2) int main(){
exit f(4) int i;
enter f(3) for (i=0; i<10; i++){
enter f(2) a[i] = f(i);
exit f(2) }
enter f(1) }
exit f(1) int f (int n) {
exit f(3) if (n<3) return 1;
exit f(5) return f(n-1)+f(n-2);
main ends }
We can make the following observation about these procedure calls.

The information needed for each invocation of a procedure is kept in a runtime data structure called an activation record (AR) or frame. The frames are kept in a stack called the control stack.
At any point in time the number of frames on the stack is the current depth of procedure calls. For example, in the fibonacci execution shown above when f(4) is active there are three activation records on the control stack.
ARs vary with the language and compiler implementation. Typical components are described and pictured below. In the diagrams the stack grows down the page.
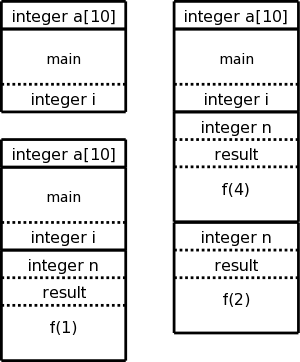
The diagram on the right shows (part of) the control stack for the fibonacci example at three points during the execution. In the upper left we have the initial state, We show the global variable a, although it is not in an activation record and actually is allocated before the program begins execution (it is statically allocated; recall that the stack and heap are each dynamically allocated). Also shown is the activation record for main, which contains storage for the local variable i.
Below the initial state we see the next state when main has called f(1) and there are two activation records, one for main and one for f. The activation record for f contains space for the parameter n and and also for the result. There are no local variables in f.
At the far right is a later state in the execution when f(4) has been called by main and has in turn called f(2). There are three activation records, one for main and two for f. It is these multiple activations for f that permits the recursive execution. There are two locations for n and two for the result.
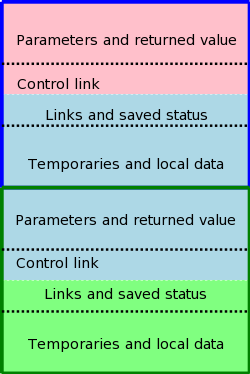
The calling sequence, executed when one procedure (the caller) calls another (the callee), allocates an activation record (AR) on the stack and fills in the fields. Part of this work is done by the caller; the remainder by the callee. Although the work is shared, the AR is called the callee's AR.
Since the procedure being called is defined in one place, but called from many, there are more instances of the caller activation code than of the callee activation code. Thus it is wise, all else being equal, to assign as much of the work to the callee.
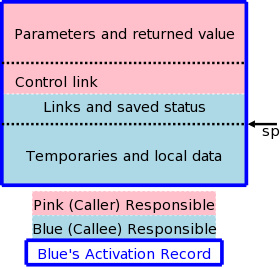
The top picture illustrates the situation where a pink procedure (the caller) calls a blue procedure (the callee). Also shown is Blue's AR. Note that responsibility for this single AR is shared by both procedures. The picture is just an approximation: For example, the returned value is actually the Blue's responsibility (although the space might well be allocated by Pink. Also some of the saved status, e.g., the old sp, is saved by Pink.
The bottom picture shows what happens when Blue, the callee, itself
calls a green procedure and thus Blue is also a caller.
You can see that Blue's responsibility includes part of its AR as
well as part of Green's.

Note that varagrs are supported.
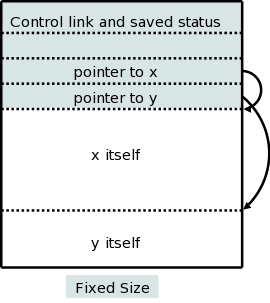
There are two flavors of variable-length data.
It is the second flavor that we wish to allocate on the stack. The goal is for the (called) procedure to be able to access these arrays using addresses determinable at compile time even though the size of the arrays (and hence the location of all but the first) is not know until the program is called and indeed often differs from one call to the next.
The solution is to leave room for pointers to the arrays in the AR. These are fixed size and can thus be accessed using static offsets. Then when the procedure is invoked and the sizes are known, the pointers are filled in and the space allocated.
A small change caused by storing these variable size items on the stack is that it no longer is obvious where the real top of the stack is located relative to sp. Consequently another pointer (call it real-top-of-stack) is also kept. This is used on a call to tell where the new allocation record should begin.
As we shall see the ability of procedure p to access data declared outside of p (either declared globally outside of all procedures or declared inside another procedure q) offers interesting challenges.
In languages like standard C without nested procedures, visible names are either local to the procedure in question or are declared globally.
With nested procedures a complication arises. Say g is nested inside f. So g can refer to names declared in f. These names refer to objects in the AR for f; the difficulty is finding that AR when g is executing. We can't tell at compile time where the (most recent) AR for f will be relative to the current AR for g since a dynamically-determined number of routines could have been called in the middle.
There is an example in the next section. in which g refers to x, which is declared in the immediately outer scope (main) but the AR is 2 away because f was invoked in between. (In that example you can tell at compile time what was called in what order, but with a more complicated program having data-dependent branches, it is not possible.)
As we have discussed, the 1e, which you have, uses pascal, which many of you don't know. The 2e, which you don't have uses C, which you do know.
Since pascal supports nested procedures, this is what the 1e uses to give examples.
The 2e asserts (correctly) that C doesn't have nested procedures so introduces ML, which does (and is quite slick), but which unfortunately many of you don't know and I haven't used. Fortunately a common extension to C is to permit nested procedures. In particular, gcc supports nested procedures. To check my memory I compiled and ran the following program.
#include <stdio.h>
int main (int argc, char *argv[])
{
int x = 10;
void g(int y)
{
int z = x;
return;
}
int f (int y)
{
g(y);
return y+1;
}
printf("The answer is %d\n", f(x));
return 0;
}
The program compiles without errors and the correct answer of 11 is printed.
So we can use C (really the GCC, et al extension of C).
Outermost procedures have nesting depth 1. Other procedures have nesting depth 1 more than the nesting depth of the immediately outer procedure. In the example above main has nesting depth 1; both f and g have nesting depth 2.
The AR for a nested procedure contains an access link that points to the AR of the (most recent activation of the immediately outer procedure). So in the example above the access link for all activations of f and g would point to the AR of the (only) activation of main. Then for a procedure P to access a name defined in the 3-outer scope, i.e., the unique outer scope whose nesting depth is 3 less than that of P, you follow the access links three times.
The question is how are the access links maintained.
Let's assume there are no procedure parameters. We are also assuming that the entire program is compiled at once. For multiple files the main issues involve the linker, which is not covered in this course. I do cover it a little in the OS course.
Without procedure parameters, the compiler knows the name of the called procedure and, since we are assuming the entire program is compiled at once, knows the nesting depth.
Let the caller be procedure R (the last letter in caller) and let the called procedure be D. Let N(f) be the nesting depth of f. I did not like the presentation in 2e (which had three cases and I think did not cover the example above). I made up my own and noticed it is much closer to 1e (but makes clear the direct recursion case, which is explained in 2e). I am surprised to see a regression from 1e to 2e, so make sure I have not missed something in the cases below.
P() {
D() {...}
P1() {
P2() {
...
Pk() {
R(){... D(); ...}
}
...
}
}
}
Our goal while creating the AR for D at the call from R is to set
the access link to point to the AR for P.
Note that this entire structure in the skeleton code shown is
visible to the compiler.
Thus, the current (at the time of the call) AR is the one for R
and if we follow the access links k+1 times we get a pointer to
the AR for P, which we can then place in the access link for the
being-created AR for D.
When k=0 we get the gcc code I showed before and also the case of direct recursion where D=R.
Basically skipped. The problem is that, if f calls g giving with a parameter of h (or a pointer to h in C-speak) and the g calls this parameter (i.e., calls h), g might not know the context of h. The solution is for f to pass to g the pair (h, the access link of h) instead of just passing h. Naturally, this is done by the compiler, the programmer is unaware of access links.
Basically skipped. In theory access links can form long chains (in practice nesting depth rarely exceeds a dozen or so). A display is an array in which entry i points to the most recent (highest on the stack) AR of depth i.
Almost all of this section is covered in the OS class.
Covered in OS.
Covered in Architecture.
Covered in OS.
Covered in OS.
Stack data is automatically deallocated when the defining procedure returns. What should we do with heap data explicated allocated with new/malloc?
The manual method is to require that the programmer explicitly deallocate these data. Two problems arise.
loop
allocate X
use X
forget to deallocate X
As this program continues to run it will require more and more
storage even though is actual usage is not increasing
significantly.
allocate X
use X
deallocate X
100,000 lines of code not using X
use X
Both can be disastrous.
The system detects data that cannot be accessed (no direct or indirect references exist) and deallocates the data automatically.
Covered in programming languages???
Skipped
Skipped
Skipped.