Compilers

6.4.4: Translation of Array References

Let's go over this carefully, especially the generated code and its use of addresses.

The book (both additions are the same in this respect) included a[i] as a legal address for three-address code. Last time, I did not appreciate the significance of this address form and thought it was just a convenience. In fact it is a special form.

• In lisp there is a simple evaluation rule. To evaluate (a b c d) you
  1. Evaluate all four components.
  2. Confirm that the first component evaluates to a function.
  3. Invoke this function passing as arguments the values calculated for the other three components.
• But is not always applied.
• Instead there are special forms that are evaluated differently.
• For example (setq a b) does not evaluate a prior to invoking setq.
• A similar thing is happening with a[i]. It is a special form in that we don't use the address of i but instead the value of i is added to the address of a.

1. Since we are restricted to one dimensional arrays, the full code generation for the address of an element is not hard and
2. I thought it would be instructive to see the full address generation without hiding some of it under the covers.

It was definitely instructive for me! The rules for addresses in 3-address code also include

    a = &b
    a = *b
    *a = b
  

I believe the SDD on the right if given a[3]=5, with a an integer array will generate

    t$1 = 3*4    // t$n are the temporary names from new TEMP()
    t$2 = &a
    t$3 = t$2 + t$1
    *t3 = 5
  

I also added an & to the non-array production lv→ID so that both could be handled by the same semantic rule for as→lv=e.

Homework: Write the SDD using the a[i] special form instead of the & and * special forms.

This is an exciting moment. At long last we can compile a full program!

Recall the program we could partially handle.

    procedure test () is
        y : integer;
        type t is array of real;
        x : t[10];
    begin
        y = 5;        // we haven't yet done statements
        x[2] = y;     // type error?
    end;
  

What about the possible type error?

1. We could ignore errors.
2. We could assume the intermediate language permits mismatched types. Final code generation would then need to generate conversion code or signal an error.
3. We could change the program to use only one type.
4. We could learn about type checking and conversions.

Let's take the last option.

Homework: What code is generated for the program written above?

6.5: Type Checking

Remark: We are back to chapter 6 in 1e.

Type Checking includes several aspects.

1. The language comes with a type system, i.e., a set of rules saying what types can appear where.
2. The compiler assigns a type expression to parts of the source program.
3. The compiler checks that the type usage in the program conforms to the type system for the language.

All type checking could be done at run time: The compiler generates code to do the checks. Some languages have very weak typing; for example, variables can change their type during execution. Often these languages need run-time checks. Examples include lisp, snobol, apl.

A sound type system guarantees that all checks can be performed prior to execution. This does not mean that a given compiler will make all the necessary checks.

An implementation is strongly typed if compiled programs are guaranteed to run without type errors.

6.5.1: Rules for Type Checking

There are two forms of type checking.

1. We will learn type synthesis where the types of parts are used to infer the type of the whole. For example, integer+real=real.
2. Type inference is very slick. The type of a construct is determined from usage. This permits languages like ML to check types even though names need not be declared.

We consider type checking for expessions. Checking statements is very similar. View the statement as a function having its components as arguments and returning void.

6.5.2: Type Conversions

A very strict type system would do no automatic conversion. Instead it would offer functions for the programer to explicitly convert between selected types. Then either the program has compatible types or is in error.

However, we will consider a more liberal approach in which the language permits certain implicit conversions that the compiler is to supply. This is called type coercion. Explicit conversions supplied by the programmer are called casts.

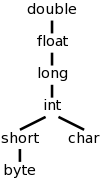
We continue to work primarily with the two types used in lab 3, namely integer and real, and postulate a unary function denoted (real) that converts an integer into the real having the same value. Nonetheless, we do consider the more general case where there are multiple types some of which have coercions (often called widening). For example in C/Java, int can be widened to long, which in turn can be widened to float as shown in the figure to the right.

Mathematically the hierarchy on the right is a partially order set (poset) in which each pair of elements has a least upper bound (LUB). For many binary operators (all the arithmetic ones we are considering, but not exponentiation) the two operands are converted to the LUB. So adding a short to a char, requires both to be converted to an int. Adding a byte to a float, requires the byte to be converted to a float (the float remains a float and is not converted).

Checking and Coercing Types for Addition

The steps for addition, subtraction, multiplication, and division are all essentially the same: Convert each types if necessary to the LUB and then perform the arithmetic on the (converted or original) values. Note that conversion requires the generation of code.

Two functions are convenient.

1. LUB(t1,t2) returns the type that is the LUB of the two given types. It signals an error if there is no LUB, for example if one of the types is an array.
2. widen(a,t,w,newcode,newaddr). Given an address a of type t, and a (hopefully) wider address w, produce the instructions newcode needed so that the address newaddr is the conversion of address a to type w.

LUB is simple, just look at the address latice. If one of the type arguments is not in the lattice, signal an error; otherwise find the lowest common ancestor.

widen is more interesting. It involves n² cases for n types. Many of these are error cases (e.g., if t wider than w). Below is the code for our situation with two possible types integer and real. The four cases consist of 2 nops (when t=w), one error (t=real; w=integer) and one conversion (t=integer; w=real).

    widen (a:addr, t:type, w:type, newcode:string, newaddr:addr)
      if t=w
        newcode = ""
        newaddr = a
      else if t=integer and w=real
        newaddr = new Temp()
        newcode = gen(newaddr = (real) a)
      else signal error
  

With these two functions it is not hard to modify the rules to catch type errors and perform coercions for arithmetic expressions.

1. Maintain the type of each operand by defining type attributes for e, t, and f.
2. Coerce each operand to the LUB.

This requires that we have type information for the base entities, identifiers and numbers. The lexer can supply the type of the numbers. We retrieve it via get(NUM.type).

It is more interesting for the identifiers. We insert that information when we process declarations. So we now have another semantic check: Is the identifier declared before it is used?

I will use the function get(ID.type), which returns the type from the identifier table and signals an error if it is not there. The original SDD for assignment statements was here and the changes for arrays was here.

Assignment Statements With Type Checks and Coercions

Production	Semantic Rule
as → lv = e	widen(e.addr, e.type, lv.type, as.code1, as.addr1) as.code = lv.code || e.code || as.code1 || gen(*lv.addr1 = as.addr1)
lv → ID	lv.addr = new TEMP()
	lv.type = get(ID.type)
	lv.code = gen(lv.addr = &get(ID.lexeme))
lv → let ae	lv.addr = ae.addr
	lv.type = ae.type
	lv.code = ae.code
ae → ID [ e ]	ae.type = getBaseType(ID.entry.type) ae.t1 = new Temp() ae.t2 = new Temp() ae.addr = new Temp() ae.code = e.code || gen(ae.t1 = e.addr * getBaseWidth(ID.entry)) ||           gen(ae.t2 = &get(ID.lexeme)) ||           gen(ae.addr = ae.t2 + ae.t1)
e → t	e.addr = t.addr
	e.type = t.type
	e.code = t.code
e → e1 + t	e.addr = new Temp()
	e.type = LUB(e1.type, t.type)
	widen(e1.addr, e1.type, e.type, e.code1, e.addr1) widen(t.addr, t.type, e.type, e.code2, e.addr2) e.code = e1.code || t.code || e.code1 || e.code2 || gen(e.addr = e.addr1 + e.addr2)
e → e1 - t	e.addr = new Temp()
	e.type = LUB(e1.type, t.type)
	widen(e1.addr, e1.type, e.type, e.code1, e.addr1) widen(t.addr, t.type, e.type, e.code2, e.addr2) e.code = e1.code || t.code || e.code1 || e.code2 || gen(e.addr = e.addr1 - e.addr2)
t → f	t.addr = f.addr
	t.type = f.type
	t.code = f.code
t → t1 * f	t.addr = new Temp()
	t.type = LUB(t1.type, f.type)
	widen(t1.addr, t1.type, t.type, t.code1, t.addr1) widen(f.addr, f.type, t.type, t.code2, t.addr2) t.code = t1.code || f.code || t.code1 || t.code2 || gen(t.addr = t.addr1 * t.addr2)
t → t1 / f	t.addr = new Temp()
	t.type = LUB(t1.type, f.type)
	widen(t1.addr, t1.type, t.type, t.code1, t.addr1) widen(f.addr, f.type, t.type, t.code2, t.addr2) t.code = t1.code || f.code || t.code1 || t.code2 || gen(t.addr = t.addr1 / t.addr2)
f → ( e )	f.addr = e.addr
	f.type = e.type
	f.code = e.code
f → ID	f.addr = get(ID.lexeme)
	f.type = get(ID.type)
	f.code = ""
f → NUM	f.addr = get(NUM.lexeme)
	f.type = get(NUM.type)
	f.code = ""

Homework: Same question as the previous homework (What code is generated for the program written above?). But the answer is different!

6.5.3: Overloading of Functions and Operators

Skipped.

Overloading is when a function or operator has several definitions depending on the types of the operands and result.

6.5.4: Type Inference and Polymorphic Functions

Skipped.

6.5.5: An Algorithm for Unification

Skipped.

6.6: Control Flow

Remark: Section 8.4 in 1e.

Control flow includes the study of Boolean expressions, which have two roles.

1. They can be computed and treated similar to integers or real. Once can declare Boolean variables, there are boolean constants and boolean operators. There are also relational operators that produce Boolean values from arithmetic operands. From this point of view, Boolean expressions are similar to the expressions we have already treated. Our previous semantic rules could be modified to generate the code needed to evaluate these expressions.
2. They are used in certain statements that alter the normal flow of control. In this regard, we have something new to learn.

6.6.1: Boolean Expressions

One question that comes up with Boolean expressions is whether both operands need be evaluated. If we need to evaluate A or B and find that A is true, must we evaluate B? For example, consider evaluating

     A=0 OR  3/A < 1.2
  

This comes up some times in arithmetic as well. Consider A*F(x). If the compiler knows that for this run A is zero must it evaluate F(x)? Don't forget that functions can have side effects,

6.6.2: Short-Circuit Code

This is also called jumping code. Here the Boolean operators AND, OR, and NOT do not appear in the generated instruction stream. Instead we just generate jumps to either the true branch or the false branch

6.6.3: Flow-of-Control Statements

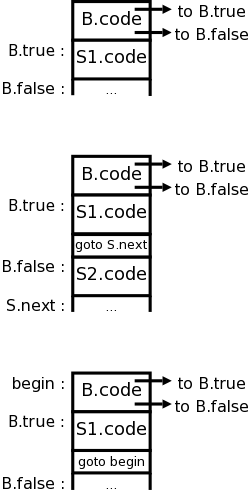
This time I will follow 2e and use C/Java grammar rather than lab 3 grammar since lab 3 is basically a subset.

So our grammar is (S for statement, B for boolean expression)

  S → if ( B ) S1
  S → if ( B ) S1 else S2
  S → while ( B ) S1

The idea is simple.

1. In this section we will produce an SDD for these three compound statements under the assumption that the SDD for B generates jumps to the labels B.true and B.false (depending of course on whether B is true or false).
2. In the next section we give the needed SDD for B.
3. I don't know why the sections aren't in the reverse order and I came close to reversing the order of presentation.
4. The diagrams on the right give the idea.
5. The table below gives the details.

Homework: Give the SDD for a repeat statement
Repeat S while B

6.6.4: Control-Flow Translation of Boolean Expressions

Do on the board the translation of

    if ( x < 5 || x > 10 && x == y ) x = 3 ;
  

We get

        if x < 5 goto L2
        goto L3
    L3: if x > 10 goto L4
	goto L1
    L4: if x == y goto L2
	goto L1
    L2: x = 3
  

Note that there are three extra gotos. One is a goto the next statement. Two others could be eliminated by using ifFalse.