
Example: Work out the parsing table for
E → T E'
E' → + T E' | ε
T → F T'
T' → * F T' | ε
F → ( E ) | id
| FIRST | FOLLOW | |
|---|---|---|
| E | ( id | $ ) |
| E' | ε + | $ ) |
| T | ( id | + $ ) |
| T' | ε * | + $ ) |
| F | ( id | * + $ ) |
We already computed FIRST and FOLLOW as shown on the right. The table skeleton is
| Nonter- minal | Input Symbol | |||||
|---|---|---|---|---|---|---|
| + | * | ( | ) | id | $ | |
| E | ||||||
| E' | ||||||
| T | ||||||
| T' | ||||||
| F | ||||||
Homework: Produce the predictive parsing table for
This illustrates the standard technique for eliminating recursion by keeping the stack explicitly. The runtime improvement can be considerable.
Skipped.

Now we start with the input string, i.e., the bottom (leaves) of what will become the parse tree, and work our way up to the start symbol.
For bottom up parsing, we are not as fearful of left recursion as we were with top down. Our first few examples will use the left recursive expression grammar
E → E + T | T
T → T * F | F
F → ( E ) | id
Remember that running a production in reverse
, i.e., replacing
the RHS by the LHS is called reducing.
So our goal is to reduce the input string to the start symbol.
On the right is a movie of parsing id*id in a bottom-up fashion. Note the way it is written. For example, from step 1 to 2, we don't just put F above id*id. We draw it as we do because it is the current top of the tree (really forest) and not the bottom that we are working on so we want the top to be in horizontal line and hence easy to read.
The tops of the forest are the roots of the subtrees present in the
diagram.
For the movie those are
id * id, F * id, T * F, T, E
Note that (since the reduction successfully reaches the start
symbol) each of these sets of roots is a sentential form.
The steps from one frame of the movie, when viewed going down the
page, are reductions (replace the RHS of a production by the LHS).
Naturally, when viewed going up the page, we have a derivation
(replace LHS by RHS).
For our example the derivation is
E ⇒ T ⇒ T * F ⇒
T * id ⇒ F * id ⇒ id * id
Note that this is a rightmost derivation and hence each of the sets of roots identified above is a right sentential form. So the reduction we did in the movie was a rightmost derivation in reverse.
Remember that for a non-ambiguous grammar there is only one rightmost derivation and hence there is only one rightmost derivation in reverse.
Remark: You cannot simply scan the string (the
roots of the forest) from left to right and choose the first
substring that matches the RHS of some production.
If you try it in our movie you will reduce T to E right after T
appears.
The result is not a right sentential form.
| Right Sentential Form | Handle | Reducing Production |
|---|---|---|
| id1 * id2 | id1 | F → id |
| F * id2 | F | T → F |
| T * id2 | id2 | F → id |
| T * F | T * F | E → T * F |
The strings that are reduced during the reverse of a rightmost derivation are called the handles. For our example, this is shown in the table on the right.
Note that the string to the right of the handle must contain only terminals. If there was a non-terminal to the right, it would have been reduced in the RIGHTmost derivation that leads to this right sentential form.
Often instead of referring to a derivation A→α as a handle, we call α the handle. I should say a handle because there can be more than one if the grammar is ambiguous.
So (assuming a non-ambiguous grammar) the rightmost derivation in reverse can be obtained by constantly reducing the handle in the current string.
Homework: 4.23 a c
We use two data structures for these parsers.
shifted(see below) onto the stack will be terminals, but some are
reducedto nonterminals. The bottom of the stack is marked with $ and initially the stack is empty (i.e., has just $).
| Stack | Input | Action |
|---|---|---|
| $ | id1*id2$ | shift |
| $id1 | *id2$ | reduce F→id |
| $F | *id2$ | reduce T→F |
| $T | *id2$ | shift |
| $T* | id2$ | shift |
| $T*id2 | $ | reduce F→id |
| $T*F | $ | reduce T→T*F |
| $T | $ | reduce E→T |
| $E | $ | accept |
A technical point, which explains the usage of a stack is that a handle is always at the TOS. See the book for a proof; the idea is to look at what rightmost derivations can do (specifically two consecutive productions) and then trace back what the parser will do since it does the reverse operations (reductions) in the reverse order.
We have not yet discussed how to decide whether to shift or reduce when both are possible. We have also not discussed which reduction to choose if multiple reductions are possible. These are crucial question for bottom up (shift-reduce) parsing and will be addressed.
Homework: 4.23 b
There are grammars (non-LR) for which no viable algorithm can decide whether to shift or reduce when both are possible or which reduction to perform when several are possible. However, for most languages, choosing a good lexer yields an LR(k) language of tokens. For example, ada uses () for both function calls and array references. If the lexer returned id for both array names and procedure names then a reduce/reduce conflict would occur when the stack was ... id ( id and the input ) ... since the id on TOS should be reduced to parameter if the first id was a procedure name and to expr if the first id was an array name. A better lexer (and an assumption, which is true in ada, that the declaration must precede the use) would return proc-id when it encounters a lexeme corresponding to a procedure name. It does this by constructing the symbol table it builds.
Remark: Both editions do a warm up
before
getting down to business with full LR parsing.
The first edition does operator precedence and covers SLR in the
middle of the section on LR parsing.
The second omits operator precedence and does SLR here.
I am following the second since operator precedence is no longer
widely used and I believe SLR will be more helpful
when trying to understand full LR and hence serves as a better
introduction the subject.
Indeed, I will have much more to say about SLR than the other LR schemes. The reason is that SLR is simpler to understand, but does capture the essence of shift-reduce, bottom-up parsing. The disadvantage of SLR is that there are LR grammars that are not SLR.
I will just say the following about operator precedence. We shall see that a major consideration in all the bottom-up, shift-reduce parsers is deciding when to shift and when to reduct. Consider parsing A+B*C in C/java/etc. When the stack is A+B and the remaining input is *C, the parser needs to know whether to reduce A+B or shift in * and then C. (Really the A+B will probably by now be more like E+T.) The idea of operator precedence is that we give * higher precedence so when the parser see * on the input it knows not to reduce +. More details are in the first (i.e., your) edition of the text.
The text's presentation is somewhat controversial.
Most commercial compilers use hand-written top-down parsers of the
recursive-descent (LL not LR) variety.
Since the grammars for these languages are not LL(1), the
straightforward application of the techniques we have seen will not
work.
Instead the parsers actually look ahead further than one token, but
only at those few places where the grammar is in fact not LL(1).
Recall that (hand written) recursive descent compilers have a
procedure for each nonterminal so we can customize as needed
.
These compiler writers claim that they are able to produce much
better error messages than can readily be obtained by going to LR
(with its attendant requirement that a parser-generator be used since
the parsers are too large to construct by hand).
Note that compiler error messages is a very important user interface
issue and that with recursive descent one can augment the procedure
for a nonterminal with statements like
if (nextToken == X) then error(expected Y here
)
Nonetheless, the claims made by the text are correct, namely.
We now come to grips with the big question
:
How does a shift-reduce parser know when to shift and when to
reduce?
This will take a while to answer in a satisfactory manner.
The unsatisfactory answer is that the parser has tables that say in
each situation
whether to shift or reduce (or announce error,
or announce acceptance).
To begin the path toward the answer, we need several definitions.
An item is a production with a marker saying how far the parser has gotten with this production. Formally,
Definition: An (LR(0)) item of a grammar is a production with a dot added somewhere to the RHS.
Examples:
The item E → E · + T signifies that the parser has just processed input that is derivable from E and will look for input derivable from + T.
Line 4 indicates that the parser has just seen the entire
RHS and must consider reducing it to E.
Important: consider
does not mean do
.
The parser groups certain items together into states. As we shall see, the items with a given state are treated similarly.
Our goal is to construct first the canonical LR(0)
collection of states and then a DFA called the LR(0) automaton
(technically not a DFA since no dead state
).
To construct the canonical LR(0) collection formally and present the parsing algorithm in detail we shall
Augmenting the grammar is easy. We simply add a new start state S' and one production S'→S. The purpose is to detect success, which occurs when the parser is ready to reduce S to S'.
So our example grammar
E → E + T | T
T → T * F | F
F → ( E ) | id
is augmented by adding the production E' → E.
I hope the following interlude will prove helpful. In preparing to present SLR, I was struck how it looked like we were working with a DFA that came from some (unspecified and unmentioned) NFA. It seemed that by first doing the NFA, I could give some rough insight. Since for our current example the NFA has more states and hence a bigger diagram, let's consider the following extremely simple grammar.
E → E + T
E → T
T → id
When augmented this becomes
E' → E
E → E + T
E → T
T → id
When the dots are added we get 10 items (4 from the second
production, 2 each from the other three).
See the diagram at the right.
We begin at E'→.E since it is the start item.
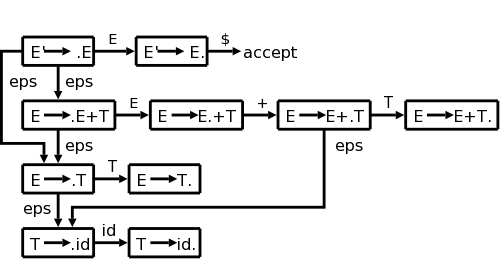
Note that there are really four kinds
of edges.
If we were at the item E→E·+T (the dot indicating that we have seen an E and now need a +) and shifted a + from the input to the stack we would move to the item E→E+·T. If the dot is before a non-terminal, the parser needs a reduction with that non-terminal as the LHS.
Now we come to the idea of closure, which I illustrate in the diagram with the ε's. Please note that this is rough, we are not doing regular expressions again, but I hope this will help you understand the idea of closure, which like ε in regular production leads to nondeterminism.
Look at the start state. The placement of the dot indicates that we next need to see an E. Since E is a nonterminal, we won't see it in the input, but will instead have to generate it via a production. Thus by looking for an E, we are also looking for any production that has E on the LHS. This is indicated by the two ε's leaving the top left box. Similarly, there are ε's leaving the other three boxes where the dot is immediately to the left of a nonterminal.
 As with regular expressions, we combine
As with regular expressions, we combine n-items
connected by
an ε arc into a d-item
.
The actual terminology used is that we combine these items into a
set of items (later referred to as a state).
There is another combination that occurs.
The top two n-items in the left column are combined into the same
d-item and both n-items have E transitions (outgoing arcs labeled
E).
Since we are considering these two n-items to be the same d-item and
the arcs correspond to the same transition, the two targets (the
top two n-items in the 2nd column) are combined.
A d-item has all the outgoing arcs of the original n-items
it contains.
This is the way we converted an NFAs into a DFA in the previous chapter.
I0, I1, etc are called (LR(0)) item sets, and
the collection with the arcs (i.e., the DFA) is called the LR(0)
automaton.
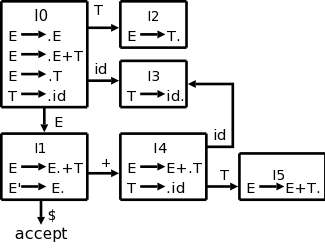
| Stack | Symbols | Input | Action |
|---|---|---|---|
| 0 | id+id$ | Shift to 3 | |
| 03 | id | +id$ | Reduce by T→id |
| 02 | T | +id$ | Reduce by E→T. |
| 01 | E | +id$ | Shift to 4 |
| 014 | E+ | id$ | Shift to 3 |
| 0143 | E+id | $ | Reduce by T→id |
| 0145 | E+T | $ | Reduce by E→E+T |
| 01 | E | $ | Accept |
We start in the initial state with the stack empty and the input full. The $'s are just end markers. From state 0, called I0 in my diagram (following the book they are called I's since they are sets of items), we can only shift in the id (the nonterminals will appear in the symbols column). This brings us to I3 so we push a 3 onto the stack
In I3 we see a completed production in the box (the
dot is on the extreme right).
Thus we can reduce by this production.
To reduce we pop the stack for each symbol in the RHS since we are
replacing the RHS by the LHS; this time the RHS has one symbol so we
pop the stack once and also remove one symbol.
The stack corresponds to moves so we are undoing the move to 3 and
we are temporarily
in 0 again.
But the production has a T on the LHS so we follow the T production
from 0 to 2, push T onto Symbols, and push 2 onto the stack.
In I2 we again see a completed production and do another reduction, which brings us to 1.
The next two steps are shifts of + and id.
We then reduce the id to T and are in step 5 ready for the
big one
.
The reduction in 5 has three symbols on the RHS so we pop (back up) three times again temporarily landing in 0, but the RHS puts us in 1.
Perfect! We have just E as a symbol and the input is empty so we are ready to reduce by E'→E, which signifies acceptance.
Now we rejoin the book and say it more formally.