
Homework: 4.1 a, c, d
The leaves of a parse tree (or of any other tree), when read left to right, are called the frontier of the tree. For a parse tree we also call them the yield of the tree.
If you are given a derivation starting with a single nonterminal,
A ⇒ x1 ⇒ x2 ... ⇒ xn
it is easy to write a parse tree with A as the root and
xn as the leaves.
Just do what (the productions contained in) each step of the
derivation says.
The LHS of each production is a nonterminal in the frontier of the
current tree so replace it with the RHS to get the next tree.
Do this for both the leftmost and rightmost derivations of id+id above.
So there can be many derivations that wind up with the same final tree.
But for any parse tree there is a unique leftmost derivation the produces that tree and a unique rightmost derivation that produces the tree. There may be others as well (e.g., sometime choose the leftmost nonterminal to expand; other times choose the rightmost).
Homework: 4.1 b
Recall that an ambiguous grammar is one for which there is more than one parse tree for a single sentence. Since each parse tree corresponds to exactly one leftmost (or rightmost) derivation, an ambiguous grammar is one for which there is more than one leftmost (or rightmost) derivation of a given sentence.
We know that the grammar
E → E + E | E * E | ( E ) | id
is ambiguous because we have seen (a few lectures ago) two parse
trees for
E ⇒ E + E E ⇒ E * E
⇒ id + E ⇒ E + E * E
⇒ id + E * E ⇒ id + E * E
⇒ id + id * E ⇒ id + id * E
⇒ id + id * id ⇒ id + id * E
As we stated before we prefer unambiguous grammars. Failing that, we want disambiguation rules.
Skipped
Alternatively context-free languages vs regular languages.
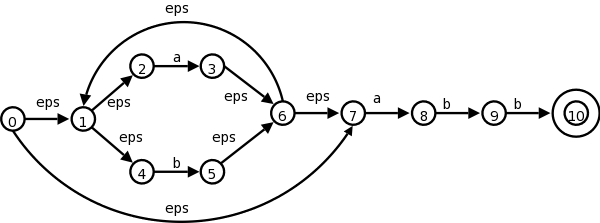
Given an RE, construct an NFA as in chapter 3.
From that NFA construct a grammar as follows.
If you trace an NFA accepting a sentence, it just corresponds to the constructed grammar deriving the same sentence. Similarly, follow a derivation and notice that at any point prior to acceptance there is only one nonterminal; this nonterminal gives the state in the NFA corresponding to this point in the derivation.
The book starts with (a|b)*abb and then uses the short NFA on the left below. Recall that the NFA generated by our construction is the longer one on the right.


The book gives the simple grammar for the short diagram.
Let's be ambitious and try the long diagram
A0 → A1 | A7
A1 → A2 | A4
A2 → a A3
A3 → A6
A4 → b A5
A5 → A6
A6 → A1 | A7
A7 → a A8
A8 → b A9
A9 → b A10
A10 → ε
Now trace a path in the NFA and see that it is just a derivation. The same is true in reverse (derivation gives path). The key is that at every stage you have only one nonterminal.
The grammar
A → a A b | ε
generates all strings of the form anbn, where
there are the same number of a's and b's.
In a sense the grammar has counted.
No RE can generate this language (proof in book).
Why have separate lexer and parser?
Recall the ambiguous grammar with the notorious dangling
else
problem.
stmt → if expr then stmt
| if expr then stmt else stmt
| other
This has two leftmost derivations for
if E1 then S1 else if E2 then S2 else S3
Do these on the board. They differ in the beginning.
In this case we can find a non-ambiguous, equivalent grammar.
stmt → matched-stmt | open-stmt
matched-stmp → if expr then matched-stmt else matched-stmt
| other
open-stmt → if expr then stmt
| if expr then matched-stmt else open-stmt
On the board try to find leftmost derivations of the problem sentence above.
We did special cases in chapter 2.
Now we do it right
(tm).
Previously we did it separately for one production and for two productions with the same nonterminal A on the LHS. Not surprisingly, this can be done for n such productions (together with other non-left recursive productions involving A).
Specifically we start with
A → A x1 | A x2 | ... A xn | y1 | y2 | ... ym
where the x's and y's are strings, no x is ε, and no y
begins with A.
The equivalent non-left recursive grammar is
A → y1 A' | ... | ym A'
A' → x1 A' | ... | xn A' | ε
Example: Assume x1 is + and y1 is *.
With the recursive grammar, we have the following lm derivation.
A ⇒ A + ⇒ , +
With the non-recursive grammar we have
A ⇒ , A' ⇒ , + A' ⇒ , +
This removes direct left recursion where a production with A on the left hand side begins with A on the right. If you also had direct left recursion with B, you would apply the procedure twice.
The harder general case is where you permit indirect left recursion, where, for example one production has A as the LHS and begins with B on the RHS, and a second production has B on the LHS and begins with A on the RHS. Thus in two steps we can turn A into something starting again with A. Naturally, this indirection can involve more than 2 nonterminals.
Theorem: All left recursion can be eliminated.
Proof: The book proves this for grammars that have
no ε-productions and no cycles
and has exercises
asking the reader to prove that cycles and ε-productions can
be eliminated.
We will try to avoid these hard cases.
Homework: Eliminate left recursion in the
following grammar for simple postfix expressions.
X → S S + | S S * | a
If two productions with the same LHS have their RHS beginning with the same symbol, then the FIRST sets will not be disjoint so predictive parsing (chapter 2) will be impossible and more generally top down parsing (later this chapter) will be more difficult as a longer lookahead will be needed to decide which production to use.
So convert A → x y1 | x y2 into
A → x A'
A' → y1 | y2
In other words factor outthe x.
Homework: Left factor your answer to the previous homework.
Although our grammars are powerful, they are not all-powerful. For example, we cannot write a grammar that checks that all variables are declared before used.
We did an example of top down parsing, namely predictive parsing, in chapter 2.
For top down parsing, we
The above has two nondeterministic choices (the nonterminal, and the production) and requires luck at the end. Indeed, the procedure will generate the entire language. So we have to be really lucky to get the input string.
Let's reduce the nondeterminism in the above algorithm by specifying which nonterminal to expand. Specifically, we do a depth-first (left to right) expansion.
We leave the choice of production nondeterministic.
We also process the terminals in the RHS, checking that they match the input. By doing the expansion depth-first, left to right, we ensure that we encounter the terminals in the order they will appear in the frontier of the final tree. Thus if the terminal does not match the corresponding input symbol now, it never will and the expansion so far will not produce the input string as desired.
Now our algorithm is
for i = 1 to n
if Xi is a nonterminal
process Xi // recursive
else if Xi (a terminal) matches current input symbol
advance input to next symbol
else // trouble Xi doesn't match and never will
Note that the trouble
mentioned at the end of the algorithm
does not signify an erroneous input.
We may simply have chosen the wrong
production in step 2.
In a general recursive descent (top-down) parser, we would support backtracking, that is when we hit the trouble, we would go back and choose another production. Since this is recursive, it is possible that no productions work for this nonterminal, because the wrong choice was made earlier.
The good news is that we will work with grammars where we can control the nondeterminism much better. Recall that for predictive parsing, the use of 1 symbol of lookahead made the algorithm fully deterministic, without backtracking.
We used FIRST(RHS) when we did predictive parsing.
Now we learn the whole truth about these two sets, which prove to be quite useful for several parsing techniques (and for error recovery).
The basic idea is that FIRST(α) tells you what the first symbol can be when you fully expand the string α and FOLLOW(A) tells what terminals can immediately follow the nonterminal A.
Definition: For any string α of grammar symbols, we define FIRST(α) to be the set of terminals that occur as the first symbol in a string derived from α. So, if α⇒*xQ for x a terminal and Q a string, then x is in FIRST(α). In addition if α⇒*ε, then ε is in FIRST(α).
Definition: For any nonterminal A, FOLLOW(A) is the set of terminals x, that can appear immediately to the right of A in a sentential form. Formally, it is the set of terminals x, such that S⇒*αAxβ. In addition, if A can be the rightmost symbol in a sentential form, the endmarker $ is in FOLLOW(A).
Note that there might have been symbols between A and x during the derivation, providing they all derived ε and eventually x immediately follows A.
Unfortunately, the algorithms for computing FIRST and FOLLOW are not as simple to state as the definition suggests, in large part caused by ε-productions.
Do the FIRST and FOLLOW sets for
E → T E'
E' → + T E' | ε
T → F T'
T' → * F T' | ε
F → ( E ) | id
Homework: Compute FIRST and FOLLOW for the postfix grammar S → S S + | S S * | a
The predictive parsers of chapter 2 are recursive descent parsers needing no backtracking. A predictive parser can be constructed for any grammar in the class LL(1). The two Ls stand for (processing the input) Left to right and for producing Leftmost derivations. The 1 in parens indicates that 1 symbol of lookahead is used.
Definition: A grammar is LL(1) if for all production pairs A → α | β
The 2nd condition may seem strange; it did to me for a while. Let's consider the simplest case that condition 2 is trying to avoid.
S → A b // b is in FOLLOW(A)
A → b // α=b so α derives a string beginning with b
A → ε // β=ε so β derives ε
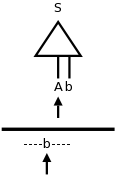
Assume we are using predictive parsing and, as illustrated in the diagram to the right, we are at A in the parse tree and b in the input. Since lookahead=b and b is in FIRST(RHS) for the top A production, we would choose that production to expand A. But this could be wrong! Remember that we don't look ahead in the tree just in the input. So we would not have noticed that the next node in the tree (i.e., in the frontier) is b. This is possible since b is in FOLLOW(A). So perhaps we should use the second A production to produce ε in the tree, and then the next node b would match the input b.
The goal is to produce a table telling us at each situation which
production to apply.
A situation
means a nonterminal in the parse tree and an
input symbol in lookahead.
So we produce a table with rows corresponding to nonterminals and columns corresponding to input symbols (including $. the endmarker). In an entry we put the production to apply when we are in that situation.
We start with an empty table M and populate it as follows. For each production A → α
strange) condition above. If ε is in FIRST(α), then α⇒*ε. Hence we should apply the production A→α, have the α go to ε and then the b (or $), which follows A will match the b in the input.
When we have finished filling in the table M, what do we do if an slot has