I start at Chapter 0 so that when we get to chapter 1, the numbering will agree with the text.
There is a web site for the course. You can find it from my home page listed above.
The course text is Aho, Seithi, and Ullman: Compilers: Principles, Techniques, and Tools
Your grade will be a function of your final exam and laboratory assignments (see below). I am not yet sure of the exact weightings for each lab and the final, but will let you know soon.
I use the upper left board for lab/homework assignments and announcements. I should never erase that board. If you see me start to erase an announcement, please let me know.
I try very hard to remember to write all announcements on the upper left board and I am normally successful. If, during class, you see that I have forgotten to record something, please let me know. HOWEVER, if I forgot and no one reminds me, the assignment has still been given.
I make a distinction between homeworks and labs.
Labs are
Homeworks are
Homeworks are numbered by the class in which they are assigned. So any homework given today is homework #1. Even if I do not give homework today, the homework assigned next class will be homework #2. Unless I explicitly state otherwise, all homeworks assignments can be found in the class notes. So the homework present in the notes for lecture #n is homework #n (even if I inadvertently forgot to write it to the upper left board).
You may solve lab assignments on any system you wish, but ...
Good methods for obtaining help include
You may write your lab in Java, C, or C++. Other languages may be possible, but please ask in advance. I need to ensure that the TA is comfortable with the language.
The rules for incompletes and grade changes are set by the school and not the department or individual faculty member. The rules set by GSAS state:
The assignment of the grade Incomplete Pass(IP) or Incomplete Fail(IF) is at the discretion of the instructor. If an incomplete grade is not changed to a permanent grade by the instructor within one year of the beginning of the course, Incomplete Pass(IP) lapses to No Credit(N), and Incomplete Fail(IF) lapses to Failure(F).
Permanent grades may not be changed unless the original grade resulted from a clerical error.
I do not assume you have had a compiler course as an undergraduate, and I do not assume you have had experience developing/maintaining a compiler.
If you have already had a compiler class, this course is probably not appropriate. For example, if you can explain the following concepts/terms, the course is probably too elementary for you.
I do assume you are an experienced programmer. There will be non-trivial programming assignments during this course. Indeed, you will write a compiler for a simple programming language.
I also assume that you have at least a passing familiarity with assembler language. In particular, your compiler will produce assembler language. We will not, however, write significant assembly-language programs.
Our policy on academic integrity, which applies to all graduate courses in the department, can be found here.
Homework Read chapter 1.
A Compiler is a translator from one language, the input or source language, to another language, the output or target language.
Often, but not always, the target language is an assembler language or the machine language for a computer processor.
Modern compilers contain two (large) parts, each of which is often subdivided. These two parts are the front end and the back end.
The front end analyzes the source program, determines its constituent parts, and constructs an intermediate representation of the program. Typically the front end is independent of the target language.
The back end synthesizes the target program from the intermediate representation produced by the front end. Typically the back end is independent of the source language.
This front/back division very much reduces the work for a compiling
system that can handle several (N) source languages and several (M)
target languages. Instead of NM compilers, we need N front ends and
M back ends. For gcc (originally standing for Gnu C Compiler, but
now standing for Gnu Compiler Collection), N=7 and M~30 so the
savings is considerable.

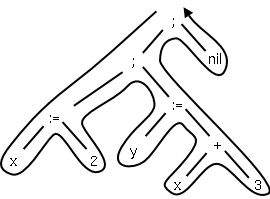
Often the intermediate form produced by the front end is
a syntax tree. In simple cases, such as that shown to the
right corresponding to the C statement sequence
x := 2; y := x + 3;
this tree has constants and
variables (and nil) for leaves and operators for internal nodes.
The back end traverses the tree in “Euler-tour” order and
generates code for each node. (This is quite oversimplified.)
Other “compiler like” applications also use analysis and synthesis. Some examples include
[preprocessor] --> [compiler] --> [assembler] --> [linker] --> [loader]
We will be primarily focused on the second element of the chain, the compiler. Our target language will be assembly language.
Preprocessors are normally fairly simple as in the C language, providing primarily the ability to include files and expand macros. There are exceptions, however. IBM's PL/I, another Algol-like language had quite an extensive preprocessor, which made available at preprocessor time, much of the PL/I language itself (e.g., loops and I believe procedure calls).
Some preprocessors essentially augment the base language, to add additional capabilities. One could consider them as compilers in their own right having as source this augmented language (say fortran augmented with statements for multiprocessor execution in the guise of fortran comments) and as target the original base language (in this case fortran). Often the “preprocessor” inserts procedure calls to implement the extensions at runtime.
Assembly code is an mnemonic version of machine code in which names, rather than binary values, are used for machine instructions, and memory addresses.
Some processors have fairly regular operations and as a result assembly code for them can be fairly natural and not-too-hard to understand. Other processors, in particular Intel's x86 line, have let us charitably say more “interesting” instructions with certain registers used for certain things.
My laptop has one of these latter processors (pentium 4) so my gcc compiler produces code that from a pedagogical viewpoint is less than ideal. If you have a mac with a ppc processor (newest macs are x86), your assembly language is cleaner. NYU's ACF features sun computers with sparc processors, which also have regular instruction sets.
No matter what the assembly language is, an assembler needs to assign memory locations to symbols (called identifiers) and use the numeric location address in the target machine language produced. Of course the same address must be used for all occurrences of a given identifier and two different identifiers must (normally) be assigned two different locations.
The conceptually simplest way to accomplish this is to make two passes over the input (read it once, then read it again from the beginning). During the first pass, each time a new identifier is encountered, an address is assigned and the pair (identifier, address) is stored in a symbol table. During the second pass, whenever an identifier is encountered, its address is looked up in the symbol table and this value is used in the generated machine instruction.
Consider the following trivial C program that computes and returns the xor of the characters in a string.
int xor (char s[]) // native C speakers say char *s
{
int ans = 0;
int i = 0;
while (s[i] != 0) {
ans = ans ^ s[i];
i = i + 1;
}
return ans;
}
The corresponding assembly language program (produced by gcc -S -fomit-frame-pointer) is
.file "xor.c" .text .globl xor .type xor, @function xor: subl $8, %esp movl $0, 4(%esp) movl $0, (%esp) .L2: movl (%esp), %eax addl 12(%esp), %eax cmpb $0, (%eax) je .L3 movl (%esp), %eax addl 12(%esp), %eax movsbl (%eax),%edx leal 4(%esp), %eax xorl %edx, (%eax) movl %esp, %eax incl (%eax) jmp .L2 .L3: movl 4(%esp), %eax addl $8, %esp ret .size xor, .-xor .section .note.GNU-stack,"",@progbits .ident "GCC: (GNU) 3.4.6 (Gentoo 3.4.6-r1, ssp-3.4.5-1.0, pie-8.7.9)"
You should be able to follow everything from xor: to ret. Indeed most of the rest can be omitted (.globl g is needed). That is the following assembly program gives the same results.
.globl xor xor: subl $8, %esp movl $0, 4(%esp) movl $0, (%esp) .L2: movl (%esp), %eax addl 12(%esp), %eax cmpb $0, (%eax) je .L3 movl (%esp), %eax addl 12(%esp), %eax movsbl (%eax),%edx leal 4(%esp), %eax xorl %edx, (%eax) movl %esp, %eax incl (%eax) jmp .L2 .L3: movl 4(%esp), %eax addl $8, %esp ret
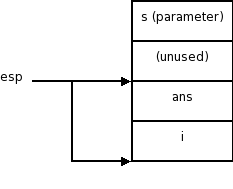
What is happening in this program?
Lab assignment 1 is available on the class web site. The programming is trivial; you are just doing inclusive (i.e., normal) OR rather than XOR I just did. The point of the lab is to give you a chance to become familiar with your compiler and assembler.
Linkers, a.k.a. linkage editors combine the output of the assembler for several different compilations. That is the horizontal line of the diagram above should really be a collection of lines converging on the linker. The linker has another input, namely libraries, but to the linker the libraries look like other programs compiled and assembled. The two primary tasks of the linker are
The assembler processes one file at a time. Thus the symbol table produced while processing file A is independent of the symbols defined in file B, and conversely. Thus, it is likely that the same address will be used for different symbols in each program. The technical term is that the (local) addresses in the symbol table for file A are relative to file A; they must be relocated by the linker. This is accomplished by adding the starting address of file A (which in turn is the sum of the lengths of all the files processed previously in this run) to the relative address.
Assume procedure f, in file A, and procedure g, in file B, are compiled (and assembled) separately. Assume also that f invokes g. Since the compiler and assembler do not see g when processing f, it appears impossible for procedure f to know where in memory to find g.
The solution is for the compiler to indicated in the output of the file A compilation that the address of g is needed. This is called a use of g When processing file B, the compiler outputs the (relative) address of g. This is called the definition of g. The assembler passes this information to the linker.
The simplest linker technique is to again make two passes. During the first pass, the linker records in its “external symbol table” (a table of external symbols, not a symbol table that is stored externally) all the definitions encountered. During the second pass, every use can be resolved by access to the table.
I will be covering the linker in more detail tomorrow at 5pm in 2250, OS Design
After the linker has done its work, the resulting “executable file” can be loaded by the operating system into central memory. The details are OS dependent. With early single-user operating systems all programs would be loaded into a fixed address (say 0) and the loader simply copies the file to memory. Today it is much more complicated since (parts of) many programs reside in memory at the same time. Hence the compiler/assembler/linker cannot know the real location for an identifier. Indeed, this real location can change.
More information is given in any OS course (e.g., 2250 given wednesdays at 5pm).
Conceptually, there are three phases of analysis with the output of one phase the input of the next. The phases are called lexical analysis or scanning, syntax analysis or parsing, and semantic analysis.
The character stream input is grouped into tokens. For example, any one of the following
x3 := y + 3; x3 := y + 3 ; x3 :=y+ 3 ;but not
x 3 := y + 3;would be grouped into
Note that non-significant blanks are normally removed during scanning. In C, most blanks are non-significant. Blanks inside strings are an exception.
Note that we could define identifiers, numbers, and the various
symbols and punctuation can be defined without recursion (compare
with parsing below).
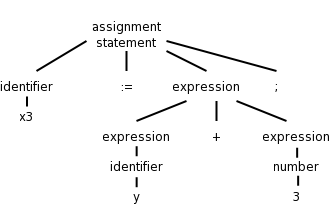
Parsing involves a further grouping in which tokens are grouped into grammatical phrases, which are normally represented in a parse tree. For example
x3 := y + 3;would be parsed into the tree on the right.
This parsing would result from a grammar containing rules such as
asst-stmt --> id := expr ;
expr --> number
| id
| expr + expr
Note the recursive definition of expression (expr). Note also the hierarchical decomposition in the figure on the right.
The division between scanning and parsing is somewhat arbitrary,
but invariably if a recursive definition is involved, it is
considered parsing not scanning.
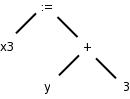
Often we utilize a simpler tree called the syntax tree with operators as interior nodes and operands as the children of the operator. The syntax tree on the right corresponds to the parse tree above it.
(Technical point.) The syntax tree represents an assignment expression not an assignment statement. In C an assignment statement includes the trailing semicolon. That is, in C (unlike in Algol) the semicolon is a statement terminator not a statement separator.
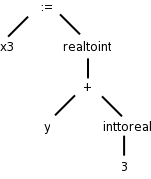
There is more to a front end than simply syntax. The compiler needs semantic information, e.g., the types (integer, real, pointer to array of integers, etc) of the objects involved. This enables checking for semantic errors and inserting type conversion where necessary.
For example, if y was declared to be a real and x3 an integer, We need to insert (unary, i.e., one operand) conversion operators “inttoreal” and “realtoint” as shown on the right.
Illustrates the use of hierarchical grouping for formatting languages (Tex and EQN are used as examples). For example shows how you can get subscripted superscripts (or superscripted subscripts)
[scanner]→[parser]→[sem anal]→[inter code gen]→[opt1]→[code gen]→[opt2]
We just examined the first three phases. Modern, high-performance
compilers, are dominated by their extensive optimization
phases, which occur before, during, and after code generation. Note
that optimization is most assuredly an inaccurate, albeit standard,
terminology, as the resulting code is not optimal.
As we have seen when discussing assemblers and linkers, a symbol table is used to maintain information about symbols. The compiler uses a symbol to maintain information across phases as well as within each phase. One key item stored with each symbol is the corresponding type, which is determined during semantic and used (among other places) during code generation.
As you have doubtless noticed, not all programming efforts produce correct programs. If the input to the compiler is not a legal source language program, errors must be detected and reported. It is often much easier to detect that the program is not legal (e.g., the parser reaches a point where the next token cannot legally occur) than to deduce what is the actual error (which may have occurred earlier). It is even harder to reliably deduce what the intended correct program should be.
The scanner converts
x3 := y + 3;into
id1 := id2 + 3 ;where id is short for identifier.
This is processed by the parser and semantic analyzer to produce the two trees shown above here and here. On some systems, the tree would not contain the symbols themselves as shown in the figures. Instead the tree would contain leaves of the form idi which in turn would refer to the corresponding entries in the symbol table.
Many compilers first generate code for an “idealized machine”. For example, the intermediate code generated would assume that the target has an unlimited number of registers and that any register can be used for any operation. Another common assumption is that all machine operations take three operands, two source and one target.
With these assumptions one generates “three-address code” by walking the semantic tree. Our example C instruction would produce
temp1 := inttoreal(3) temp2 := id2 + temp1 temp3 := realtoint(temp2) id1 := temp3
We see that three-address code can include instructions with fewer than 3 operands.
Sometimes three-address code is called quadruples because one can view the previous code sequence as
inttoreal temp1 3 -- add temp2 id2 temp1 realtoint temp3 temp2 -- assign id1 temp3 --Each “quad” has the form
operation target source1 source2
This is a very serious subject, one that we will not really do justice to in this introductory course. Some optimizations are fairly easy to see.
add temp2 id2 3.0
realtoint id1 temp2
Modern processors have only a limited number of register. Although some processors, such as the x86, can perform operations directly on memory locations, we will for now assume only register operations. Some processors (e.g., the MIPS architecture) use three-address instructions. However, some processors permit only two addresses; the result overwrites the second source. With these assumptions, code something like the following would be produced for our example, after first assigning memory locations to id1 and id2.
MOVE id2, R1 ADD #3.0, R1 RTOI R1, R2 MOVE R2, id1
I found it more logical to treat these topics (preprocessors, assemblers, linkers, and loaders) earlier.
Logically each phase is viewed as a separate program that reads input and produces output for the next phase, i.e., a pipeline. In practice some phases are combined.
We discussed this previously.
Aho, Sethi, Ullman assert only limited success in producing several compilers for a single machine using a common back end. That is a rather pessimistic view and I wonder if the 2nd edition will change in this area.
The term pass is used to indicate that the entire input is read during this activity. So two passes, means that the input is read twice. We have discussed two pass approaches for both assemblers and linkers. If we implement each phase separately and use multiple phases for some of them, the compiler will perform a large number of I/O operations, an expensive undertaking.
As a result techniques have been developed to reduce the number of passes. We will see in the next chapter how to combine the scanner, parser, and semantic analyzer into one phase. Consider the parser. When it needs another token, rather than reading the input file (presumably produced by the scanner), the parser calls the scanner instead. At selected points during the production of the syntax tree, the parser calls the “code generator”, which performs semantic analysis as well as generating a portion of the intermediate code.
One problem with combining phases, or with implementing a single phase in one pass, is that it appears that an internal form of the entire program will need to be stored in memory. This problem arises because the downstream phase may need early in its execution information that the upstream phase produces only late in its execution. This motivated the use of symbol tables and a two pass approach. However, a clever one-pass approach is often possible.
Consider the assembler (or linker). The good case is when the definition precedes all uses so that the symbol table contains the value of the symbol prior to that value being needed. Now consider the harder case of one or more uses preceding the definition. When a not yet defined symbol is first used, an entry is placed in the symbol table, pointing to this use and indicating that the definition has not yet appeared. Further uses of the same symbol attach their addresses to a linked list of “undefined uses” of this symbol. When the definition is finally seen, the value is placed in the symbol table, and the linked list is traversed inserting the value in all previously encountered uses. Subsequent uses of the symbol will find its definition in the table.
This technique is called backpatching.
Originally, compilers were written “from scratch”, but now the situation is quite different. A number of tools are available to ease the burden.
We will study tools that generate scanners and parsers. This will involve us in some theory, regular expressions for scanners and various grammars for parsers. These techniques are fairly successful. One drawback can be that they do not execute as fast as “hand-crafted” scanners and parsers.
We will also see tools for syntax-directed translation and automatic code generation. The automation in these cases is not as complete.
Finally, there is the large area of optimization. This is not automated; however, a basic component of optimization is “data-flow analysis” (how are values transmitted between parts of a program) and there are tools to help with this task.
Homework: Read chapter 2.
Implement a very simple compiler.
The source language is infix expressions consisting of digits, +,
and -; the target is postfix expressions with the same components.
The compiler will convert
7+4-5 to 74+5-.
Actually, our simple compiler will handle a few other operators as well.
We will tokenize
the input (i.e., write a scanner), model
the syntax of the source, and let this syntax direct the translation.
This will be “done right” in the next two chapters.
A context-free grammar (CFG) consists of
Example:
Terminals: 0 1 2 3 4 5 6 7 8 9 + -
Nonterminals: list digit
Productions: list → list + digit
list → list - digit
list → digit
digit → 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
Start symbol: list
Watch how we can generate the input 7+4-5 starting with the start symbol, applying productions, and stopping when no productions are possible (we have only terminals).
list → list - digit
→ list - 5
→ list + digit - 5
→ list + 4 - 5
→ digit + 4 - 5
→ 7 + 4 - 5
Homework: 2.1a, 2.1c, 2.2a-c (don't worry about “justifying” your answers).
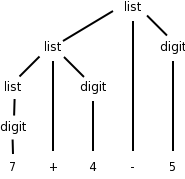
The compiler front end runs the above procedure in reverse! It starts with the string 7+4-5 and gets back to list (the “start” symbol). Reaching the start symbol means that the string is in the language generated by the grammar. While running the procedure in reverse, the front end builds up the parse tree on the right.
You can read off the productions from the tree. For any internal (i.e.,non-leaf) tree node, its children give the right hand side (RHS) of a production having the node itself as the LHS.
The leaves of the tree, read from left to right, is called the yield of the tree. We call the tree a derivation of its yield from its root. The tree on the right is a derivation of 7+4-5 from list.
Homework: 2.1b
An ambiguous grammar is one in which there are two or more parse trees yielding the same final string. We wish to avoid such grammars.
The grammar above is not ambiguous. For example 1+2+3 can be parsed only one way; the arithmetic must be done left to right. Note that I am not giving a rule of arithmetic, just of this grammar. If you reduced 2+3 to list you would be stuck since it is impossible to generate 1+list.
Homework: 2.3 (applied only to parts a, b, and c of 2.2)
Our grammar gives left associativity. That is, if you traverse the
tree in postorder and perform the indicated arithmetic you will
evaluate the string left to right. Thus 8-8-8 would evaluate to
-8. If you wished to generate right associativity (normally
exponentiation is right associative, so 2**3**2 gives 512 not 64),
you would change the first two productions to
list → digit + list and list → digit - list
We normally want * to have higher precedence than +. We do this by using an additional nonterminal to indicate the items that have been multiplied. The example below gives the four basic arithmetic operations their normal precedence unless overridden by parentheses. Redundant parentheses are permitted. Equal precedence operations are performed left to right.
expr → expr + term | expr - term | term term → term * factor | term / factor | factor factor → digit | ( expr ) digit → 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
We use | to indicate that a nonterminal has multiple possible right hand side. So
A → B | Cis simply shorthand for
A → B A → C
Do the examples 1+2/3-4*5 and (1+2)/3-4*5 on the board.
Note how the precedence is enforced by the grammar; slick!
Keywords are very helpful for distinguishing statements from one another.
stmt → id := expr
| if expr then stmt
| if expr then stmt else stmt
| while expr do stmt
| begin opt-stmts end
opt-stmts → stmt-list | ε
stmt-list → stmt-list ; stmt | stmt
Remark:
Homework: 2.16a, 2.16b
Specifying the translation of a source language construct in terms of attributes of its syntactic components.

Operator after operand. Parentheses are not needed. The normal notation we used is called infix. If you start with an infix expression, the following algorithm will give you the equivalent postfix expression.
One question is, given say 1+2-3, what is E, F and op? Does E=1+2, F=3, and op=+? Or does E=1, F=2-3 and op=+? This is the issue of precedence mentioned above. To simplify the present discussion we will start with fully parenthesized infix expressions.
Example: 1+2/3-4*5
Example: Now do (1+2)/3-4*5
We want to “decorate” the parse trees we construct with “annotations” that give the value of certain attributes of the corresponding node of the tree. We will do the example of translating infix to postfix with 1+2/3-4*5. We use the following grammar, which follows the normal arithmetic terminology where one multiplies and divides factors to obtain terms, which in turn are added and subtracted to form expressions.
expr → expr + term | expr - term | term term → term * factor | term / factor | factor factor → digit | ( expr ) digit → 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
This grammar supports parentheses, although our example does not use them. On the right is a “movie” in which the parse tree is build from this example.
The attribute we will associate with the nodes is the text to be used to print the postfix form of the string in the leaves below the node. In particular the value of this attribute at the root is the postfix form of the entire source.
The book does a simpler grammar (no *, /, or parentheses) for a simpler example. You might find that one easier. The book also does another grammar describing commands to give a robot to move north, east, south, or west by one unit at a time. The attributes associated with the nodes are the current position (for some nodes, including the root) and the change in position caused by the current command (for other nodes).
Definition: A syntax-directed definition is a grammar together with a set of “semantic rules” for computing the attribute values. A parse tree augmented with the attribute values at each node is called an annotated parse tree.
For the bottom-up approach I will illustrate now, we annotate a node after having annotated its children. Thus the attribute values at a node can depend on the children of the node but not the parent of the node. We call these synthesized attributes, since they are formed by synthesizing the attributes of the children.
In chapter 5, when we study top-down annotations as well, we will introduce “inherited” attributes that are passed down from parents to children.
We specify how to synthesize attributes by giving the semantic rules together with the grammar. That is we give the syntax directed definition.
| Production | Semantic Rule |
|---|---|
| expr → expr1 + term | expr.t := expr1.t || term.t || '+' |
| expr → expr1 - term | expr.t := expr1.t || term.t || '-' |
| expr → term | expr.t := term.t |
| term → term1 * factor | term.t := term1.t || factor.t || '*' |
| term → term1 / factor | term.t := term1.t || factor.t || '/' |
| term → factor | term.t := factor.t |
| factor → digit | factor.t := digit.t |
| factor → ( expr ) | factor.t := expr.t |
| digit → 0 | digit.t := '0' |
| digit → 1 | digit.t := '1' |
| digit → 2 | digit.t := '2' |
| digit → 3 | digit.t := '3' |
| digit → 4 | digit.t := '4' |
| digit → 5 | digit.t := '5 |
| digit → 6 | digit.t := '6' |
| digit → 7 | digit.t := '7' |
| digit → 8 | digit.t := '8' |
| digit → 9 | digit.t := '9' |
We apply these rules bottom-up (starting with the geographically lowest productions, i.e., the lowest lines on the page) and get the annotated graph shown on the right. The annotation are drawn in green.
Homework: Draw the annotated graph for (1+2)/3-4*5.
As mentioned in this chapter we are annotating bottom-up. This corresponds to doing a depth-first traversal of the (unannotated) parse tree to produce the annotations. It is often called a postorder traversal because a parent is visited after (i.e., post) its children are visited.
The bottom-up annotation scheme generates the final result as the annotation of the root. In our infix → postfix example we get the result desired by printing the root annotation. Now we consider another technique that produces its results incrementally.
Instead of giving semantic rules for each production (and thereby generating annotations) we can embed program fragments called semantic actions within the productions themselves.
In diagrams the semantic action is connected to the node with a distinctive, often dotted, line. The placement of the actions determine the order they are performed. Specifically, one executes the actions in the order they are encountered in a postorder traversal of the tree.
Definition: A syntax-directed translation scheme is a context-free grammar with embedded semantic actions.
For our infix → postfix translator, the parent either just
passes on the attribute of its (only) child or concatenates them
left to right and adds something at the end. The equivalent
semantic actions would be either to print the new item or print
nothing.
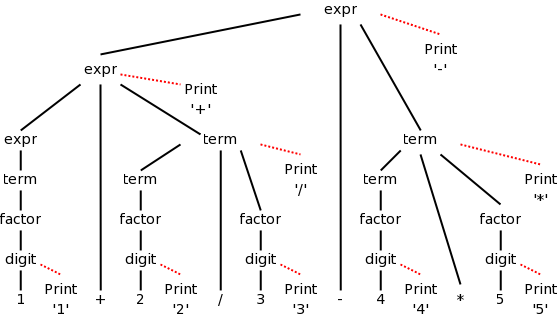
Here are the semantic actions corresponding to a few of the rows of the table above. Note that the actions are enclosed in {}.
expr → expr + term { print('+') }
expr → expr - term { print('-') }
term → term / factor { print('/') }
term → factor { null }
digit → 3 { print('3') }
The diagram for 1+2/3-4*5 with attached semantic actions is shown on the right.
Given an input, e.g. our favorite 1+2/3-4*5, we just do a depth first (postorder) traversal of the corresponding diagram and perform the semantic actions as they occur. When these actions are print statements as above, we can be said to be emitting the translation.
Do a depth first traversal of the diagram on the board, performing the semantic actions as they occur, and confirm that the translation emitted is in fact 123/+45*-, the postfix version of 1+2/3-4*5
Homework: Produce the corresponding diagram for (1+2)/3-4*5.
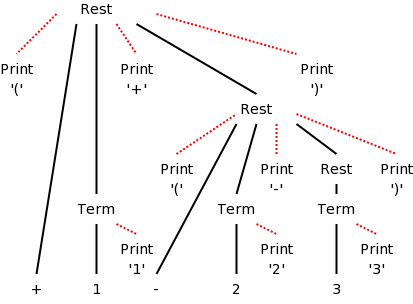
When we produced postfix, all the prints came at the end (so that the children were already “printed”. The { actions } do not need to come at the end. We illustrate this by producing infix arithmetic (ordinary) notation from a prefix source.
In prefix notation the operator comes first so +1-23 evaluates to zero. Consider the following grammar. It translates prefix to infix for the simple language consisting of addition and subtraction of digits between 1 and 3 without parentheses (prefix notation and postfix notation do not use parentheses). The resulting parse tree for +1-23 is shown on the right. Note that the output language (infix notation) has parentheses.
rest → + term rest | - term rest | term term → 1 | 2 | 3
The table below shows the semantic actions or rules needed for our
translator.
| Production with Semantic Action | Semantic Rule |
|---|---|
| rest → { print('(') } + term { print('+') } rest { print(')') } | rest.t := '(' || term.t || '+' || rest.t || ')' |
| rest → { print('(') } - term { print('-') } rest { print(')') } | rest.t := '(' || term.t || '-' || rest.t || ')' |
| rest → term | rest.t := term.t |
| term → 1 { print('1') } | term.t := '1' |
| term → 2 { print('2') } | term.t := '2' |
| term → 3 { print('3') } | term.t := '3' |
Homework: 2.8.
If the semantic rules of a syntax-directed definition all have the property that the new annotation for the left hand side (LHS) of the production is just the concatenation of the annotations for the nonterminals on the RHS in the same order as the nonterminals appear in the production, we call the syntax-directed definition simple. It is still called simple if new strings are interleaved with the original annotations. So the example just done is a simple syntax-directed definition.
Remark: We shall see later that, in many cases a simple syntax-directed definition permits one to execute the semantic actions while parsing and not construct the parse tree at all.
Remarks:
Objective: Given a string of tokens and a grammar, produce a parse tree yielding that string (or at least determine if such a tree exists).
We will learn both top-down (begin with the start symbol, i.e. the root of the tree) and bottom up (begin with the leaves) techniques.
In the remainder of this chapter we just do top down, which is easier to implement by hand, but is less general. Chapter 4 covers both approaches.
Tools (so called “parser generators”) often use bottom-up techniques.
In this section we assume that the lexical analyzer has already
scanned the source input and converted it into a sequence of tokens.

Consider the following simple language, which derives a subset of the types found in the (now somewhat dated) programming language Pascal. I am using the same example as the book so that the compiler code they give will be applicable.
We have two nonterminals, type, which is the start symbol, and simple, which represents the “simple” types.
There are 8 terminals, which are tokens produced by the lexer and correspond closely with constructs in pascal itself. I do not assume you know pascal. (The authors appear to assume the reader knows pascal, but do not assume knowledge of C.) Specifically, we have.
The productions are
type → simple
type → ↑ id
type → array [ simple ] of type
simple → integer
simple → char
simple → num dotdot num
Parsing is easy in principle and for certain grammars (e.g., the two above) it actually is easy. The two fundamental steps (we start at the root since this is top-down parsing) are
When programmed this becomes a procedure for each nonterminal that chooses a production for the node and calls procedures for each nonterminal in the RHS. Thus it is recursive in nature and descends the parse tree. We call these parsers “recursive descent”.
The big problem is what to do if the current node is the LHS of more than one production. The small problem is what do we mean by the “next” node needing a subtree.
The easiest solution to the big problem would be to assume that there is only one production having a given terminal as LHS. There are two possibilities
expr → term + term - 9
term → factor / factor
factor → digit
digit → 7
But this is very boring. The only possible sentence
is 7/7+7/7-9
expr → term + term
term → factor / factor
factor → ( expr )
This is even worse; there are no (finite) sentences. Only an
infinite sentence beginning (((((((((.
So this won't work. We need to have multiple productions with the same LHS.
How about trying them all? We could do this! If we get stuck where the current tree cannot match the input we are trying to parse, we would backtrack.
Instead, we will look ahead one token in the input and only choose productions that can yield a result starting with this token. Furthermore, we will (in this section) restrict ourselves to predictive parsing in which there is only production that can yield a result starting with a given token. This solution to the big problem also solves the small problem. Since we are trying to match the next token in the input, we must choose the leftmost (nonterminal) node to give children to.
Let's return to pascal array type grammar and consider the three
productions having type as LHS. Even when I write the short
form
type → simple | ↑ id | array [ simple ] of type
I view it as three productions.
For each production P we wish to consider the set FIRST(P) consisting of those tokens that can appear as the first symbol of a string derived from the RHS of P. We actually define FIRST(RHS) rather than FIRST(P), but I often say “first set of the production” when I should really say “first set of the RHS of the production”.
Definition: Let r be the RHS of a production P. FIRST(r) is the set of tokens that can appear as the first symbol in a string derived from r.
To use predictive parsing, we make the following
Assumption: Let P and Q be two productions with the same LHS. Then FIRST(P) and FIRST(Q) are disjoint. Thus, if we know both the LHS and the token that must be first, there is (at most) one production we can apply. BINGO!
This table gives the FIRST sets for our pascal array type example.
| Production | FIRST |
|---|---|
| type → simple | { integer, char, num } |
| type → ↑ id | { ↑ } |
| type → array [ simple ] of type | { array } |
| simple → integer | { integer } |
| simple → char | { char } |
| simple → num dotdot num | { num } |
The three productions with type as LHS have disjoint FIRST sets. Similarly the three productions with simple as LHS have disjoint FIRST sets. Thus predictive parsing can be used. We process the input left to right and call the current token lookahead since it is how far we are looking ahead in the input to determine the production to use. The movie on the right shows the process in action.
Homework:
A. Construct the corresponding table for
rest → + term rest | - term rest | term term → 1 | 2 | 3B. Can predictive parsing be used?
End of Homework:.
Not all grammars are as friendly as the last example. The first complication is when ε occurs in a RHS. If this happens or if the RHS can generate ε, then ε is included in FIRST.
But ε would always match the current input position!
The rule is that if lookahead is not in FIRST of any production with the desired LHS, we use the (unique!) production (with that LHS) that has ε as RHS.
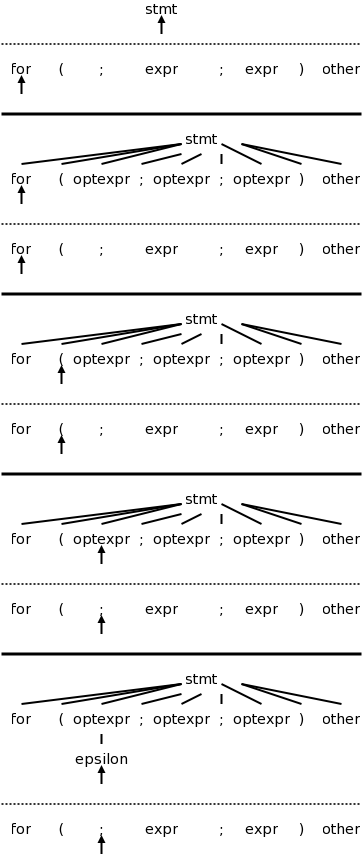
The second edition, which I just obtained now does a C instead of a pascal example. The productions are
stmt → expr ;
| if ( expr ) stmt
| for ( optexpr ; optexpr ; optexpr ) stmt
| other
optexpr → expr | ε
For completeness, on the right is the beginning of a movie for the C example. Note the use of the ε-production at the end since no other entry in FIRST will match ;
Predictive parsers are fairly easy to construct as we will now see. Since they are recursive descent parsers we go top-down with one procedure for each nonterminal. Do remember that we must have disjoint FIRST sets for all the productions having a given nonterminal as LHS.
The book has code at this point. We will see code later in this chapter.
Another complication. Consider
expr → expr + term
expr → term
For the first production the RHS begins with the LHS. This is called left recursion. If a recursive descent parser would pick this production, the result would be that the next node to consider is again expr and the lookahead has not changed. An infinite loop occurs.
Consider instead
expr → term rest
rest → + term rest
rest → ε
Both pairs of productions generate the same possible token strings,
namely
term + term + ... + term
The second pair is called right recursive since the RHS ends (has on
the right) the LHS.
If you draw the parse trees generated, you will see
that, for left recursive productions, the tree grows to the left; whereas,
for right recursive, it grows to the right.
Note also that, according to the trees generated by the first pair,
the additions are performed right to left; whereas, for the second
pair, they are performed left to right.
That is, for
term + term + term
the tree from the first pair has the left + at the top (why?);
whereas, the tree from the second pair has the right + at the top.
In general, for any A, R, α, and β, we can replace the pair
A → A α | β
with the triple
A → β R
R → α R | ε
For the example above A is “expr”, R is “rest”, α is “+ term”, and β is “term”.
Objective: an infix to postfix translator for expressions. We start with just plus and minus, specifically the expressions generated by the following grammar. We include a set of semantic actions with the grammar. Note that finding a grammar for the desired language is one problem, constructing a translator for the language given a grammar is another problem. We are tackling the second problem.
expr → expr + term { print('+') }
expr → expr - term { print('-') }
expr → term
term → 0 { print('0') }
. . .
term → 9 { print('9') }
One problem that we must solve is that this grammar is left recursive.
We prefer not to have superfluous nonterminals as they make the parsing less efficient. That is why we don't say that a term produces a digit and a digit produces each of 0,...,9. Ideally the syntax tree would just have the operators + and - and the 10 digits 0,1,...,9. That would be called the abstract syntax tree. A parse tree coming from a grammar is technically called a concrete syntax tree.
We eliminate the left recursion as we did in 2.4. This time there
are two operators + and - so we replace the triple
A → A α | A β | γ
with the quadruple
A → γ R
R → α R | β R | ε
This time we have actions so, for example
α is + term { print('+') }
However, the formulas still hold and we get
expr → term rest
rest → + term { print('+') } rest
| - term { print('-') } rest
| ε
term → 0 { print('0') }
. . .
| 9 { print('9') }
The C code is in the book. Note the else ; in rest(). This corresponds to the epsilon production. As mentioned previously. The epsilon production is only used when all others fail (that is why it is the else arm and not the then or the else if arms).
These are (useful) programming techniques.
In the first edition this is about 40 lines of C code, 12 of which are single { or }. The second edition has equivalent code in java.
Converts a sequence of characters (the source) into a sequence of tokens. A lexeme is the sequence of characters comprising a single token.
These do not become tokens so that the parser need not worry about them.
The 2nd edition moves the discussion about
x<y versus x<=y
into this new section.
I have left it 2 sections ahead to more closely agree with our
(first edition).
This chapter considers only numerical integer constants. They are computed one digit at a time by value=10*value+digit. The parser will therefore receive the token num rather than a sequence of digits. Recall that our previous parsers considered only one digit numbers.
The value of the constant is stored as the attribute of the token num. Indeed <token,attribute> pairs are passed from the scanner to the parser.
The C statement
sum = sum + x;
contains 4 tokens. The scanner will convert the input into
id = id + id ; (id standing for identifier).
Although there are three id tokens, the first and second represent
the lexeme sum; the third represents x. These must be
distinguished. Many language keywords, for example
“then”, are syntactically the same as identifiers.
These also must be distinguished. The symbol table will accomplish
these tasks.
Care must be taken when one lexeme is a proper subset of another.
Consider
x<y versus x<=y
When the < is read, the scanner needs to read another character
to see if it is an =. But if that second character is y, the
current token is < and the y must be “pushed back”
onto the input stream so that the configuration is the same after
scanning < as it is after scanning <=.
Also consider then versus thenewvalue, one is a keyword and the other an id.
As indicated the scanner reads characters and occasionally pushes one back to the input stream. The “downstream” interface is to the parser to which <token,attribute> pairs are passed.
A few comments on the program given in the text. One inelegance is that, in order to avoid passing a record (struct in C) from the scanner to the parser, the scanner returns the next token and places its attribute in a global variable.
Since the scanner converts digits into num's we can shorten the grammar. Here is the shortened version before the elimination of left recursion. Note that the value attribute of a num is its numerical value.
expr → expr + term { print('+') }
expr → expr - term { print('-') }
expr → term
term → num { print(num,value) }
In anticipation of other operators with higher precedence, we
introduce factor and, for good measure, include parentheses for
overriding the precedence. So our grammar becomes.
expr → expr + term { print('+') }
expr → expr - term { print('-') }
expr → term
term → factor
factor → ( expr ) | num { print(num,value) }
The factor() procedure follows the familiar recursive descent pattern: find a production with lookahead in FIRST and do what the RHS says.
The symbol table is an important data structure for the entire compiler. For the simple translator, it is primarily used to store and retrieve <lexeme,token> pairs.
insert(s,t) returns the index of a new entry storing the
pair (lexeme s, token t).
lookup(s) returns the index for x or 0 if not there.
Simply insert them into the symbol table prior to examining any input. Then they can be found when used correctly and, since their corresponding token will not be id, any use of them where an identifier is required can be flagged.
insert("div",div)Probably the simplest would be
struct symtableType {
char lexeme[BIGNUMBER];
int token;
} symtable[ANOTHERBIGNUMBER];
The space inefficiency of having a fixed size entry for all lexemes is
poor, so the authors use a (standard) technique of concatenating all
the strings into one big string and storing pointers to the beginning
of each of the substrings.
One form of intermediate representation is to assume that the target machine is a simple stack machine (explained very soon). The the front end of the compiler translates the source language into instructions for this stack machine and the back end translates stack machine instructions into instructions for the real target machine.
We use a very simple stack machine
Consider Q := Z; or A[f(x)+B*D] := g(B+C*h(x,y));. (I follow the text and use := for the assignment op, which is written = in C/C++. I am using [] for array reference and () for function call).
From a macroscopic view, we have three tasks.
Note the differences between L-values and R-values
| push v | push v (onto stack) |
|---|---|
| rvalue l | push contents of (location) l |
| lvalue l | push address of l |
| pop | pop |
| := | r-value on tos put into the location specified by l-value 2nd on the stack; both are popped |
| copy | duplicate the top of stack |
Machine instructions to evaluate an expression mimic the postfix form of the expression. That is we generate code to evaluate the left operand, then code to evaluate the write operand, and finally the code to evaluate the operation itself.
For example y := 7 * xx + 6 * (z + w) becomes
lvalue y push 7 rvalue xx * push 6 rvalue z rvalue w + * + :=
To say this more formally we define two attributes. For any nonterminal, the attribute t gives its translation and for the terminal id, the attribute lexeme gives its string representation.
Assuming we have already given the semantic rules for expr (i.e., assuming that the annotation expr.t is known to contain the translation for expr) then the semantic rule for the assignment statement is
stmt → id := expr
{ stmt.t := 'lvalue' || id.lexime || expr.t || := }
There are several ways of specifying conditional and unconditional jumps. We choose the following 5 instructions. The simplifying assumption is that the abstract machine supports “symbolic” labels. The back end of the compiler would have to translate this into machine instructions for the actual computer, e.g. absolute or relative jumps (jump 3450 or jump +500).
| label l | target of jump |
|---|---|
| goto l | |
| gofalse | pop stack; jump if value is false |
| gotrue | pop stack; jump if value is true |
| halt |
Fairly simple. Generate a new label using the assumed function newlabel(), which we sometimes write without the (), and use it. The semantic rule for an if statement is simply
stmt → if expr then stmt1 { out := newlabel();
stmt.t := expr.t || 'gofalse' out || stmt1.t || 'label' out
Rewriting the above as a semantic action (rather than a rule) we get the following, where emit() is a function that prints its arguments in whatever form is required for the abstract machine (e.g., it deals with line length limits, required whitespace, etc).
stmt → if
expr { out := newlabel; emit('gofalse', out); }
then
stmt1 { emit('label', out) }
Don't forget that expr is itself a nonterminal. So by the time we reach out:=newlabel, we will have already parsed expr and thus will have done any associated actions, such as emit()'ing instructions. These instructions will have left a boolean on the tos. It is this boolean that is tested by the emitted gofalse.
More precisely, the action written to the right of expr will be the third child of stmt in the tree. Since a postorder traversal visits the children in order, the second child “expr” will have been visited (just) prior to visiting the action.
Look how simple it is! Don't forget that the FIRST sets for the productions having stmt as LHS are disjoint!
procedure stmt
integer test, out;
if lookahead = id then // first set is {id} for assignment
emit('lvalue', tokenval); // pushes lvalue of lhs
match(id); // move past the lhs]
match(':='); // move past the :=
expr; // pushes rvalue of rhs on tos
emit(':='); // do the assignment (Omitted in book)
else if lookahead = 'if' then
match('if'); // move past the if
expr; // pushes boolean on tos
out := newlabel();
emit('gofalse', out); // out is integer, emit makes a legal label
match('then'); // move past the then
stmt; // recursive call
emit('label', out) // emit again makes out legal
else if ... // while, repeat/do, etc
else error();
end stmt;
Full code for a simple infix to postfix translator. This uses the concepts developed in 2.5-2.7 (it does not use the abstract stack machine material from 2.8). Note that the intermediate language we produced in 2.5-2.7, i.e., the attribute .t or the result of the semantic actions, is essentially the final output desired. Hence we just need the front end.
The grammar with semantic actions is as follows. All the actions come at the end since we are generating postfix. this is not always the case.
start → list eof
list → expr ; list
list → ε // would normally use | as below
expr → expr + term { print('+') }
| expr - term { print('-'); }
| term
term → term * factor { print('*') }
| term / factor { print('/') }
| term div factor { print('DIV') }
| term mod factor { print('MOD') }
| factor
factor → ( expr )
| id { print(id.lexeme) }
| num { print(num.value) }
Eliminate left recursion to get
start → list eof
list → expr ; list
| ε
expr → term moreterms
moreterms → + term { print('+') } moreterms
| - term { print('-') } moreterms
| ε
term | factor morefactors
morefactors → * factor { print('*') } morefactors
| / factor { print('/') } morefactors
| div factor { print('DIV') } morefactors
| mod factor { print('MOD') } morefactors
| ε
factor → ( expr )
| id { print(id.lexeme) }
| num { print(num.value) }
Show “A+B;” on board starting with “start”.
Contains lexan(), the lexical analyzer, which is called by the parser to obtain the next token. The attribute value is assigned to tokenval and white space is stripped.
| lexme | token | attribute value |
|---|---|---|
| white space | ||
| sequence of digits | NUM | numeric value |
| div | DIV | |
| mod | MOD | |
| other seq of a letter then letters and digits | ID | index into symbol table |
| eof char | DONE | |
| other char | that char | NONE |
Using a recursive descent technique, one writes routines for each nonterminal in the grammar. In fact the book combines term and morefactors into one routine.
term() {
int t;
factor();
// now we should call morefactorsl(), but instead code it inline
while(true) // morefactor nonterminal is right recursive
switch (lookahead) { // lookahead set by match()
case '*': case '/': case DIV: case MOD: // all the same
t = lookahead; // needed for emit() below
match(lookahead) // skip over the operator
factor(); // see grammar for morefactors
emit(t,NONE);
continue; // C semantics for case
default: // the epsilon production
return;
Other nonterminals similar.
The routine emit().
The insert(s,t) and lookup(s) routines described previously are in symbol.c The routine init() preloads the symbol table with the defined keywords.
Does almost nothing. The only help is that the line number, calculated by lexan() is printed.
One reason is that much was deliberately simplified. Specifically note that
Also, I presented the material way too fast to expect full understanding.
Homework: Read chapter 3.
Two methods to construct a scanner (lexical analyzer).
Note that the speed (of the lexer not of the code generated by the compiler) and error reporting/correction are typically much better for a handwritten lexer. As a result most production-level compiler projects write their own lexers
The lexer is called by the parser when the latter is ready to process another token.
The lexer also might do some housekeeping such as eliminating whitespace and comments. Some call these tasks scanning, but others call the entire task scanning.
After the lexer, individual characters are no longer examined by the compiler; instead tokens (the output of the lexer) are used.
Why separate lexical analysis from parsing? The reasons are basically software engineering concerns.
Note the circularity of the definitions for lexeme and pattern.
Common token classes.
Homework: 3.3.
We saw an example of attributes in the last chapter.
For tokens corresponding to keywords, attributes are not needed since the name of the token tells everything. But consider the token corresponding to integer constants. Just knowing that the we have a constant is not enough, subsequent stages of the compiler need to know the value of the constant. Similarly for the token identifier we need to distinguish one identifier from another. The normal method is for the attribute to specify the symbol table entry for this identifier.
We saw in this movie an example where parsing got “stuck” because we reduced the wrong part of the input string. We also learned about FIRST sets that enabled us to determine which production to apply when we are operating left to right on the input. For predictive parsers the FIRST sets for a given nonterminal are disjoint and so we know which production to apply. In general the FIRST sets might not be disjoint so we have to try all the productions whose FIRST set contains the lookahead symbol.
All the above assumed that the input was error free, i.e. that the source was a sentence in the language. What should we do when the input is erroneous and we get to a point where no production can be applied?
The simplest solution is to abort the compilation stating that the program is wrong, perhaps giving the line number and location where the parser could not proceed.
We would like to do better and at least find other errors. We could perhaps skip input up to a point where we can begin anew (e.g. after a statement ending semicolon), or perhaps make a small change to the input around lookahead so that we can proceed.
Determining the next lexeme often requires reading the input beyond the end of that lexeme. For example, to determine the end of an identifier normally requires reading the first whitespace character after it. Also just reading > does not determine the lexeme as it could also be >=. When you determine the current lexeme, the characters you read beyond it may need to be read again to determine the next lexeme.
The book illustrates the standard programming technique of using two (sizable) buffers to solve this problem.
A useful programming improvement to combine testing for the end of a buffer with determining the character read.
The chapter turns formal and, in some sense, the course begins.
The book is fairly careful about finite vs infinite sets and also uses
(without a definition!) the notion of a countable set.
(A countable set is either a finite set or one whose elements can be
put into one to one correspondence with the positive integers.
That is, it is a set whose elements can be counted.
The set of rational numbers, i.e., fractions in lowest terms, is
countable;
the set of real numbers is uncountable, because it is strictly
bigger, i.e., it cannot be counted.)
We should be careful to distinguish the empty set φ from the
empty string ε.
Formal language theory is a beautiful subject, but I shall suppress
my urge to do it right
and try to go easy on the formalism.
We will need a bunch of definitions.
Definition: An alphabet is a finite set of symbols.
Example: {0,1}, presumably φ (uninteresting), ascii, unicode, ebcdic, latin-1.
Definition: A string over an alphabet is a finite sequence of symbols from that alphabet. Strings are often called words or sentences.
Example: Strings over {0,1}: ε, 0, 1, 111010. Strings over ascii: ε, sysy, the string consisting of 3 blanks.
Definition: The length of a string is the number of symbols (counting duplicates) in the string.
Example: The length of allan, written |allan|, is 5.
Definition: A language over an alphabet is a countable set of strings over the alphabet.
Example: All grammatical English sentences with five, eight, or twelve words is a language over ascii. It is also a language over unicode.
Definition: The concatenation of strings s and t is the string formed by appending the string t to s. It is written st.
Example: εs = sε = s for any string s.
We view concatenation as a product (see Monoid in wikipedia http://en.wikipedia.org/wiki/Monoid). It is thus natural to define s0=ε and si+1=sis.
Example: s1=s, s4=ssss.
A prefix of a string is a portion starting from the beginning and a suffix is a portion ending at the end. More formally,
Definitions: A prefix of s is any string obtained from s by removing (possibly zero) characters from the end of s.
A suffix is defined analogously and a substring of s is obtained by deleting a prefix and a suffix.
Example: If s is 123abc, then
(1) s itself and ε are each a prefix, suffix, and a substring.
(2) 12 are 123a are prefixes.
(3) 3abc is a suffix.
(4) 23a is a substring.
Definitions: A proper prefix of s is a prefix of s other than ε and s itself. Similarly, proper suffixes and proper substrings of s do not include ε and s.
Definition: A subsequence of s is formed by deleting (possibly) positions from s. We say positions rather than characters since s may for example contain 5 occurrences of the character Q and we only want to delete a certain 3 of them.
Example: issssii is a subsequence of Mississippi.
Homework: 3.1b, 3.5 (c and e are optional).
Definition: The union of L1 and L2 is simply the set-theoretic union, i.e., it consists of all words (strings) in either L1 or L2.
Example: The union of {Grammatical English sentences with one, three, or five words} with {Grammatical English sentences with two or four words} is {Grammatical English sentences with five or fewer words}.
Definition: The concatenation of L1 and L2 is the set of all strings st, where s is a string of L1 and t is a string of L2.
We again view concatenation as a product and write LM for the concatenation of L and M.
Examples:: The concatenation of {a,b,c} and {1,2} is {a1,a2,b1,b2,c1,c2}. The concatenation of {a,b,c} and {1,2,ε} is {a1,a2,b1,b2,c1,c2,a,b,c}.
Definition: As with strings, it is natural to
define powers of a language L.
L0={ε}, which is not φ.
Li+1=LiL.
Definition: The (Kleene) closure of L,
denoted L* is
L0 ∪ L1 ∪ L2 ...
Definition: The positive closure of L,
denoted L+ is
L1 ∪ L2 ...
Example: {0,1,2,3,4,5,6,7,8,9}+ gives
all unsigned integers, but with some ugly versions.
It has 3, 03, 000003.
{0} ∪ ( {1,2,3,4,5,6,7,8,9} ({0,1,2,3,4,5,6,7,8,9,0}* ) )
seems better.
In these notes I may write * for * and + for +, but that is strictly speaking wrong and I will not do it on the board or on exams or on lab assignments.
Example: {a,b}* is
{ε,a,b,aa,ab,ba,bb,aaa,aab,aba,abb,baa,bab,bba,bbb,...}.
{a,b}+ is {a,b,aa,ab,ba,bb,aaa,aab,aba,abb,baa,bab,bba,bbb,...}.
{ε,a,b}* is {ε,a,b,aa,ab,ba,bb,...}.
{ε,a,b}+ is the same as {ε,a,b}*.
The book gives other examples based on L={letters} and D={digits}, which you should read..
The idea is that the regular expressions over an alphabet consist
of
ε, the alphabet, and expressions using union, concatenation, and *,
but it takes more words to say it right.
For example, I didn't include ().
Note that (A ∪ B)* is definitely not A* ∪ B* (* does not
distribute over ∪) so we
need the parentheses.
The book's definition includes many () and is more complicated than I think is necessary. However, it has the crucial advantages of being correct and precise.
The wikipedia entry doesn't seem to be as precise.
I will try a slightly different approach, but note again that there is nothing wrong with the book's approach (which appears in both first and second editions, essentially unchanged).
Definition: The regular expressions and associated languages over an alphabet consist of
Parentheses, if present, control the order of operations. Without parentheses the following precedence rules apply.
The postfix unary operator * has the highest precedence. The book mentions that it is left associative. (I don't see how a postfix unary operator can be right associative or how a prefix unary operator such as unary - could be left associative.)
Concatenation has the second highest precedence and is left associative.
| has the lowest precedence and is left associative.
The book gives various algebraic laws (e.g., associativity) concerning these operators.
The reason we don't include the positive closure is that for any RE
r+ = rr*.
Homework: 3.6 a and b.
These will look like the productions of a context free grammar we saw previously, but there are differences. Let Σ be an alphabet, then a regular definition is a sequence of definitions
d1 → r1
d2 → r2
...
dn → rn
where the d's are unique and not in Σ andNote that each di can depend on all the previous d's.
Example: C identifiers can be described by the following regular definition
letter_ → A | B | ... | Z | a | b | ... | z | _
digit → 0 | 1 | ... | 9
CId → letter_ ( letter_ | digit)*
Homework: 3.7 a,b (c is optional)
There are many extensions of the basic regular expressions given above. The following three will be frequently used in this course as they are particular useful for lexical analyzers as opposed to text editors or string oriented programming languages, which have more complicated regular expressions.
All three are simply shorthand. That is, the set of possible languages generated using the extensions is the same as the set of possible languages generated without using the extensions.
Examples:
C-language identifiers
letter_ → [A-Za-z_]
digit → [0-9]
CId → letter_ ( letter | digit ) *
Unsigned integer or floating point numbers
digit → [0-9] digits → digit+ number → digits (. digits)?(E[+-]? digits)?
Homework: 3.8 for the C language (you might need to read a C manual first to find out all the numerical constants in C), 3.10a.
Goal is to perform the lexical analysis needed for the following grammar.
stmt → if expr then stmt
| if expr then stmt else stmt
| ε
expr → term relop term // relop is relational operator =, >, etc
| term
term → id
| number
Recall that the terminals are the tokens, the nonterminals produce terminals.
A regular definition for the terminals is
digit → [0-9]
digits → digits+
number → digits (. digits)? (E[+-]? digits)?
letter → [A-Za-z]
id → letter ( letter | digit )*
if → if
then → then
else → else
relop → < | > | <= | >= | = | <>
| Lexeme | Token | Attribute |
|---|---|---|
| Whitespace | ws | — |
| if | if | — |
| then | then | — |
| else | else | — |
| An identifier | id | Pointer to table entry |
| A number | number | Pointer to table entry |
| < | relop | LT |
| <= | relop | LE |
| = | relop | EQ |
| <> | relop | NE |
| > | relop | GT |
| >= | relop | GE |
We also want the lexer to remove whitespace so we define a new token
ws → ( blank | tab | newline ) +where blank, tab, and newline are symbols used to represent the corresponding ascii characters.
Recall that the lexer will be called by the parser when the latter needs a new token. If the lexer then recognizes the token ws, it does not return it to the parser but instead goes on to recognize the next token, which is then returned. Note that you can't have two consecutive ws tokens in the input because, for a given token, the lexer will match the longest lexeme starting at the current position that yields this token. The table on the right summarizes the situation.
For the parser all the relational ops are to be treated the same so
they are all the same token, relop.
Naturally, other parts of the compiler will need to distinguish
between the various relational ops so that appropriate code is
generated.
Hence, they have distinct attribute values.
A transition diagram is similar to a flowchart for (a part of) the lexer. We draw one for each possible token. It shows the decisions that must be made based on the input seen. The two main components are circles representing states (think of them as decision points of the lexer) and arrows representing edges (think of them as the decisions made).
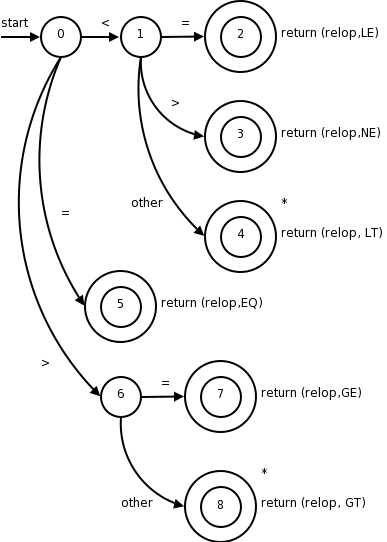
The transition diagram (3.12 in the 1st edition, 3.13 in the second) for relop is shown on the right.
too farin finding the token, one (or more) stars are drawn.
It is fairly clear how to write code corresponding to this diagram. You look at the first character, if it is <, you look at the next character. If that character is =, you return (relop,LE) to the parser. If instead that character is >, you return (relop,NE). If it is another character, return (relop,LT) and adjust the input buffer so that you will read this character again since you have used it for the current lexeme. If the first character was =, you return (relop,EQ).
The transition diagram below corresponds to the regular definition given previously.

Note again the star affixed to the final state.
Two questions remain.
then, which also match the pattern in the transition diagram?
We will continue to assume that the keywords are reserved, i.e., may not be used as identifiers. (What if this is not the case—as in Pl/I, which had no reserved words? Then the lexer does not distinguish between keywords and identifiers and the parser must.)
We will use the method mentioned last chapter and have the keywords installed into the symbol table prior to any invocation of the lexer. The symbol table entry will indicate that the entry is a keyword.
installID() checks if the lexeme is already in the table. If it is not present, the lexeme is install as an id token. In either case a pointer to the entry is returned.
gettoken() examines the lexeme and returns the token name, either id or a name corresponding to a reserved keyword.
Both installID() and gettoken() access the buffer to obtain the lexeme of interest
The text also gives another method to distinguish between identifiers and keywords.
So far we have transition diagrams for identifiers (this diagram also handles keywords) and the relational operators. What remains are whitespace, and numbers, which are the simplest and most complicated diagrams seen so far.
The diagram itself is quite simple reflecting the simplicity of the corresponding regular expression.
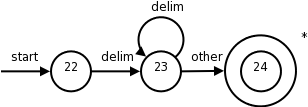
delimin the diagram represents any of the whitespace characters, say space, tab, and newline.
The diagram below is from the second edition. It is essentially a combination of the three diagrams in the first edition.
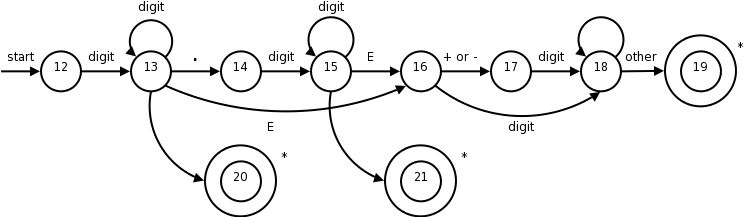
This certainly looks formidable, but it is not that bad; it follows from the regular expression.
In class go over the regular expression and show the corresponding parts in the diagram.
When an accepting states is reached, action is required but is not shown on the diagram. Just as identifiers are stored in a symbol table and a pointer is returned, there is a corresponding number table in which numbers are stored. These numbers are needed when code is generated. Depending on the source language, we may wish to indicate in the table whether this is a real or integer. A similar, but more complicated, transition diagram could be produced if they language permitted complex numbers as well.
Homework: Write transition diagrams for the regular expressions in problems 3.6 a and b, 3.7 a and b.
The idea is that we write a piece of code for each decision diagram. I will show the one for relational operations below (from the 2nd edition). This piece of code contains a case for each state, which typically reads a character and then goes to the next case depending on the character read. The numbers in the circles are the names of the cases.
Accepting states often need to take some action and return to the parser. Many of these accepting states (the ones with stars) need to restore one character of input. This is called retract() in the code.
What should the code for a particular diagram do if at one state the character read is not one of those for which a next state has been defined? That is, what if the character read is not the label of any of the outgoing arcs? This means that we have failed to find the token corresponding to this diagram.
The code calls fail(). This is not an error case. It simply means that the current input does not match this particular token. So we need to go to the code section for another diagram after restoring the input pointer so that we start the next diagram at the point where this failing diagram started. If we have tried all the diagram, then we have a real failure and need to print an error message and perhaps try to repair the input.
Note that the order the diagrams are tried is important. If the input matches more than one token, the first one tried will be chosen.
TOKEN getRelop() // TOKEN has two components
TOKEN retToken = new(RELOP); // First component set here
while (true)
switch(state)
case 0: c = nextChar();
if (c == '<') state = 1;
else if (c == '=') state = 5;
else if (c == '>') state = 6;
else fail();
break;
case 1: ...
...
case 8: retract(); // an accepting state with a star
retToken.attribute = GT; // second component
return(retToken);
The description above corresponds to the one given in the first edition.
The newer edition gives two other methods for combining the multiple transition-diagrams (in addition to the one above).
The newer version, which we will use, is called flex, the f stands for fast. I checked and both lex and flex are on the cs machines. I will use the name lex for both.
Lex is itself a compiler that is used in the construction of other compilers (its output is the lexer for the other compiler). The lex language, i.e, the input language of the lex compiler, is described in the few sections. The compiler writer uses the lex language to specify the tokens of their language as well as the actions to take at each state.
Let us pretend I am writing a compiler for a language called pink. I produce a file, call it lex.l, that describes pink in a manner shown below. I then run the lex compiler (a normal program), giving it lex.l as input. The lex compiler output is always a file called lex.yy.c, a program written in C.
One of the procedures in lex.yy.c (call it pinkLex()) is the lexer itself, which reads a character input stream and produces a sequence of tokens. pinkLex() also sets a global value yylval that is shared with the parser. I then compile lex.yy.c together with a the parser (typically the output of lex's cousin yacc, a parser generator) to produce say pinkfront, which is an executable program that is the front end for my pink compiler.
The general form of a lex program like lex.l is
declarations %% translation rules %% auxiliary functions
The lex program for the example we have been working with follows (it is typed in straight from the book).
%{
/* definitions of manifest constants
LT, LE, EQ, NE, GT, GE,
IF, THEN, ELSE, ID, NUMBER, RELOP */
%}
/* regular definitions */
delim [ \t\n]
ws {delim}*
letter [A-Za-z]
digit [0-9]
id {letter}({letter}{digit})*
number {digit}+(\.{digit}+)?(E[+-]?{digit}+)?
%%
{ws} {/* no action and no return */}
if {return(IF);}
then {return(THEN);}
else {return(ELSE);}
{id} {yylval = (int) installID(); return(ID);}
{number} {yylval = (int) installNum(); return(NUMBER);}
"<" {yylval = LT; return(RELOP);}
"<=" {yylval = LE; return(RELOP);}
"=" {yylval = EQ; return(RELOP);}
"<>" {yylval = NE; return(RELOP);}
">" {yylval = GT; return(RELOP);}
">=" {yylval = GE; return(RELOP);}
%%
int installID() {/* function to install the lexeme, whose first character
is pointed to by yytext, and whose length is yyleng,
into the symbol table and return a pointer thereto */
}
int installNum() {/* similar to installID, but puts numerical constants
into a separate table */
The first, declaration, section includes variables and constants as well as the all-important regular definitions that define the building blocks of the target language, i.e., the language that the generated lexer will analyze.
The next, translation rules, section gives the patterns of the lexemes that the lexer will recognize and the actions to be performed upon recognition. Normally, these actions include returning a token name to the parser and often returning other information about the token via the shared variable yylval.
If a return is not specified the lexer continues executing and finds the next lexeme present.
Anything between %{ and %} is not processed by lex, but instead is copied directly to lex.yy.c. So we could have had statements like
#define LT 12 #define LE 13
The regular definitions are mostly self explanatory. When a definition is later used it is surrounded by {}. A backslash \ is used when a special symbol like * or . is to be used to stand for itself, e.g. if we wanted to match a literal star in the input for multiplication.
Each rule is fairly clear: when a lexeme is matched by the left, pattern, part of the rule, the right, action, part is executed. Note that the value returned is the name (an integer) of the corresponding token. For simple tokens like the one named IF, which correspond to only one lexeme, no further data need be sent to the parser. There are several relational operators so a specification of which lexeme matched RELOP is saved in yylval. For id's and numbers's, the lexeme is stored in a table by the install functions and a pointer to the entry is placed in yylval for future use.
Everything in the auxiliary function section is copied directly to lex.yy.c. Unlike declarations enclosed in %{ %}, however, auxiliary functions may be used in the actions
The first rule makes <= one instead of two lexemes.
The second rule makes if
a keyword and not an id.
Sorry.
Sometimes a sequence of characters is only considered a certain
lexeme if the sequence is followed by specified other sequences.
Here is a classic example.
Fortran, PL/I, and some other languages do not have reserved words.
In Fortran
IF(X)=3
is a legal assignment statement and the IF is an identifier.
However,
IF(X.LT.Y)X=Y
is an if/then statement and IF is a keyword.
Sometimes the lack of reserved words makes lexical disambiguation
impossible, however, in this case the slash / operator of lex is
sufficient to distinguish the two cases.
Consider
IF / \(.*\){letter}
This only matches IF when it is followed by a ( some text a ) and a letter. The only FORTRAN statements that match this are the if/then shown above; so we have found a lexeme that matches the if token. However, the lexeme is just the IF and not the rest of the pattern. The slash tells lex to put the rest back into the input and match it for the next and subsequent tokens.
Homework: 3.11.
Homework: Modify the lex program in section 3.5.2 so that: (1) the keyword while is recognized, (2) the comparison operators are those used in the C language, (3) the underscore is permitted as another letter (this problem is easy).
The secret weapon used by lex et al to convert (compile
) its
input into a lexer.
Finite automata are like the graphs we saw in transition diagrams but they simply decide if a sentence (input string) is in the language (generated by our regular expression). That is, they are recognizers of language.
There are two types of finite automata
executionis deterministic; hence the name.
lookaheadsymbol.
Surprising Theorem: Both DFAs and NFAs are capable of recognizing the same languages, the regular languages, i.e., the languages generated by regular expressions (plus the automata can recognize the empty language).
There are certainly NFAs that are not DFAs. But the language recognized by each such NFA can also be recognized by at least one DFA.
The DFA that recognizes the same language as an NFA might be significantly larger that the NFA.
The finite automaton that one constructs naturally from a regular expression is often an NFA.
Here is the formal definition.
A nondeterministic finite automata (NFA) consists of
An NFA is basically a flow chart like the transition diagrams we have already seen. Indeed an NFA (or a DFA, to be formally defined soon) can be represented by a transition graph whose nodes are states and whose edges are labeled with elements of Σ ∪ ε. The differences between a transition graph and our previous transition diagrams are:
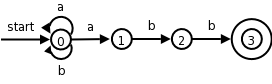
The transition graph to the right is an NFA for the regular expression (a|b)*abb, which (given the alphabet {a,b} represents all words ending in abb.
Consider aababb.
If you choose the wrong
edge for the initial a's you will get
stuck or not end at the accepting state.
But an NFA accepts a word if any path (beginning at the start
state and using the symbols in
the word in order) ends at an accepting state.
It essentially tries all such paths at once and accepts if any end
at an accepting state.
Patterns like (a|b)*abb are useful regular expressions!
If the alphabet is ascii, consider *.java.
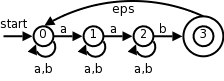
Homework: For the NFA to the right,
indicate all the paths labeled aabb.
| State | a | b | ε |
|---|---|---|---|
| 0 | {0,1} | {0} | φ |
| 1 | φ | {2} | φ |
| 2 | φ | {3} | φ |
There is an equivalent way to represent an NFA, namely a table giving, for each state s and input symbol x (and ε), the set of successor states x leads to from s. The empty set φ is used when there is no edge labeled x emanating from s. The table on the right corresponds to the transition graph above.
The downside of these tables is their size, especially if most of the entries are φ since those entries would not take any space in a transition graph.
Homework: Construct the transition table for the NFA in the previous homework problem.
An NFA accepts a string if the symbols of the string specify a path from the start to an accepting state.
Homework: Does the NFA in the previous homework accept the string aabb?
Again note that these symbols may specify several paths, some of which lead to accepting states and some that don't. In such a case the NFA does accept the string; one successful path is enough.
Also note that if an edge is labeled ε, then it can be
taken for free
.
For the transition graph above any string can just sit at state 0 since every possible symbol (namely a or b) can go from state 0 back to state 0. So every string can lead to a non-accepting state, but that is not important since if just one path with that string leads to an accepting state, the NFA accepts the string.
The language defined by an NFA or the language accepted by an NFA is the set of strings (a.k.a. words) accepted by the NFA.
So the NFA in the diagram above (not the diagram with the homework problem) accepts the same language as the regular expression (a|b)*abb.
If A is an automaton (NFA or DFA) we use L(A) for the language accepted by A.
The diagram on the right illustrates an NFA accepting the language
L(aa*|bb*).
The path
0 → 3 → 4 → 4 → 4 → 4
shows that bbbb is accepted by the NFA.
Note how the ε that labels the edge 0 → 3 does not appear in the string bbbb since ε is the empty string.
There is something weird about an NFA if viewed as a model of computation. How is a computer of any realistic construction able to check out all the (possibly infinite number of) paths to determine if any terminate at an accepting state?
We now consider a much more realistic model, a DFA.
Definition: A deterministic finite automata or DFA is a special case of an NFA having the restrictions
This is realistic. We are at a state and examine the next character in the string, depending on the character we go to exactly one new state. Looks like a switch statement to me.
Minor point: when we write a transition table for a DFA, the entries are elements not sets so there are no {} present.
Indeed a DFA is so reasonable there is an obvious algorithm for simulating it (i.e., reading a string and deciding whether or not it is in the language accepted by the DFA). We present it now.
The second edition has switched to C syntax: = is assignment == is comparison. I am going to change to this notation since I strongly suspect that most of the class is much more familiar with C/C++/java/C# than with algol60/algol68/pascal/ada (the last is my personal favorite). As I revisit past sections of the notes to fix errors, I will change the examples from algol to C usage of =. I realize that this makes the notes incompatible with the edition you have, but hope and believe that this will not cause any serious problems.
s = s0; // start state. NOTE = is assignment c = nextChar(); // aprimingread while (c != eof) { s = move(s,c); c = nextChar(); } if (s is in F, the set of accepting states) returnyeselse returnno
This is not from the book.
Do not forget the goal of the chapter is to understand lexical analysis. We saw, when looking at Lex, that regular expressions are a key in this task. So we want to recognize regular expressions (say the ones representing tokens). We are going to see two methods.
So we need to learn 4 techniques.
The list I just gave is in the order the algorithms would be applied—but you would use either 2 or (3 and 4).
The two editions differ in the order the techniques are presented, but neither does it in the order I just gave. Indeed, we just did item #4.
I will follow the order of 2nd ed but give pointers to the first edition where they differ.
Remark: If you find a particular homework question challenging, ask on the mailing list and an answer will be produced.
Remark: I forgot to assign homework for section 3.6. I have added one problem spread into three parts. It is not assigned but it is a question I believe you should be able to do.
(This is item #3 above and is done in section 3.6 in the first edition.)
The book gives a detailed proof; I am just trying to motivate the ideas.
Let N be an NFA, we construct a DFA D that accepts the same strings
as N does.
Call a state of N an N-state, and call a state of D a D-state.
The idea is that D-state corresponds to a set of N-states and hence
this is called the subset algorithm.
Specifically for each string X of symbols we consider all the
N-states that can result when N processes X.
This set of N-states is a D-state.
Let us consider the transition graph on the right, which is an NFA
that accepts strings satisfying the regular expression
(a|b)*abb.
| NFA states | DFA state | a | b |
|---|---|---|---|
| {0,1,2,4,7} | D0 | D1 | D2 |
| {1,2,3,4,6,7,8} | D1 | D1 | D3 |
| {1,2,4,5,6,7} | D2 | D1 | D2 |
| {1,2,4,5,6,7,9} | D3 | D1 | D4 |
| {1,2,4,5,6,7,10} | D4 | D1 | D2 |
The start state of D is the set of N-states that can result when N processes the empty string ε. This is called the ε-closure of the start state s0 of N, and consists of those N-states that can be reached from s0 by following edges labeled with ε. Specifically it is the set {0,1,2,4,7} of N-states. We call this state D0 and enter it in the transition table we are building for D on the right.
Next we want the a-successor of D0, i.e., the D-state
that occurs when we start at D0 and move along an edge
labeled a.
We call this successor D1.
Since D0 consists of the N-states corresponding to
ε, D1 is the N-states corresponding
to εa
=a
.
We compute the a-successor of all the N-states in D0 and
then form the ε-closure.
Next we compute the b-successor of D0 the same way and call it D2.
We continue forming a- and b-successors of all the D-states until no new D-states result (there is only a finite number of subsets of all the N-states so this process does indeed stop).
This gives the table on the right. D4 is the only D-accepting state as it is the only D-state containing the (only) N-accepting state 10.
Theoretically, this algorithm is awful since for a set with k elements, there are 2k subsets. Fortunately, normally only a small fraction of the possible subsets occur in practice.
Homework: Convert the NFA from the homework for section 3.6 to a DFA.
Instead of producing the DFA, we can run the subset algorithm as a simulation itself. This is item #2 in my list of techniques
S = ε-closure(s0);
c = nextChar();
while ( c != eof ) {
S = ε-closure(move(S,c));
c = nextChar();
}
if ( S ∩ F != φ ) return yes
; // F is accepting states
else return no
;
Slick implementation.
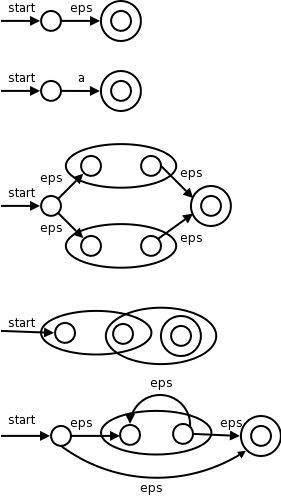
I give a pictorial proof by induction. This is item #1 from my list of techniques.
The pictures on the right illustrate the base and inductive cases.
Remarks:
Do the NFA for (a|b)*abb and see that we get the same diagram that we had before.
Do the steps in the normal leftmost, innermost order (or draw a normal parse tree and follow it).
Homework: 3.16 a,b,c
(This is on page 127 of the first edition.) Skipped.
How lexer-generators like Lex work.
We have seen simulators for DFAs and NFAs.
The remaining large question is how is the lex input converted into one of these automatons.
Also
In this section we will use transition graphs, lexer-generators do not draw pictures; instead they use the equivalent transition tables.
Recall that the regular definitions in Lex are mere conveniences
that can easily be converted to REs and hence we need only convert
REs into an FSA.
We already know how to convert a single RE into an NFA. But lex input will contain several REs (since it wishes to recognize several different tokens). The solution is to
At each of the accepting states (one for each NFA in step 1), the simulator executes the actions specified in the lex program for the corresponding pattern.
We use the algorithm for simulating NFAs presented in 3.7.2.
The simulator starts reading characters and calculates the set of states it is at.
At some point the input character does not lead to any state or we have reached the eof. Since we wish to find the longest lexeme matching the pattern we proceed backwards from the current point (where there was no state) until we reach an accepting state (i.e., the set of NFA states, N-states, contains an accepting N-state). Each accepting N-state corresponds to a matched pattern. The lex rule is that if a lexeme matches multiple patterns we choose the pattern listed first in the lex-program.
| Pattern | Action to perform |
|---|---|
| a | Action1 |
| abb | Action2 |
| a*b+ | Action3 |
Consider the example on the right with three patterns and their
associated actions and consider processing the input aaba.
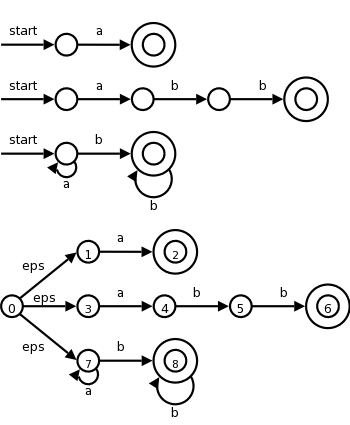
optimization.
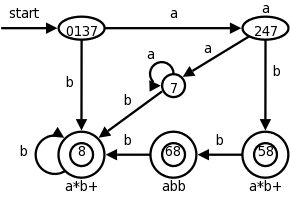
We label the accepting states with the pattern matched. If multiple patterns are matched (because the accepting D-state contains multiple accepting N-states), we use the first pattern listed (assuming we are using lex conventions).
Technical point. For a DFA, there must be a outgoing edge from each D-state for each possible character. In the diagram, when there is no NFA state possible, we do not show the edge. Technically we should show these edges, all of which lead to the same D-state, called the dead state, and corresponds to the empty subset of N-states.
This has some tricky points. Recall that this lookahead operator is for when you must look further down the input but the extra characters matched are not part of the lexeme. We write the pattern r1/r2. In the NFA we match r1 then treat the / as an ε and then match s1. It would be fairly easy to describe the situation when the NFA has only ε-transition at the state where r1 is matched. But it is tricky when there are more than one such transition.
Skipped
Skipped
Skipped
Skipped
Skipped
Homework: Read Chapter 4.
Conceptually, the parser accepts a sequence of tokens and produces a parse tree.
As we saw in the previous chapter the parser calls the lexer to obtain the next token. In practice this might not occur.
There are three classes for grammar-based parsers.
The universal parsers are not used in practice as they are inefficient.
As expected, top-down parsers start from the root of the tree and proceed downward; whereas, bottom-up parsers start from the leaves and proceed upward.
The commonly used top-down and bottom parsers are not universal. That is, there are grammars that cannot be used with them.
The LL and LR parsers are important in practice. Hand written parsers are often LL. Specifically, the predictive parsers we looked at in chapter two are for LL grammars.
The LR grammars form a larger class. Parsers for this class are usually constructed with the aid of automatic tools.
Expressions with + and *
E → E + T | T
T → T * F | F
F → ( E ) | id
This takes care of precedence, but as we saw before, gives us trouble since it is left-recursive and we did top-down parsing. So we use the following non-left-recursive grammar that generates the same language.
E → T E'
E' → + T E' | ε
T → F T'
T' → * F T' | ε
F → ( E ) | id
The following ambiguous grammar will be used for illustration, but in general we try to avoid ambiguity. This grammar does not enforce precedence.
E → E + E | E * E | ( E ) | id
There are different levels
of errors.
off by oneusage of < instead of <=.
The goals are clear, but difficult.
Print an error message when parsing cannot continue and then terminate parsing.
The first level improvement. The parser discards input until it encounters a synchronizing token. These tokens are chosen so that the parser can make a fresh beginning. Good examples are ; and }.
Locally replace some prefix of the remaining input by some string. Simple cases are exchanging ; with , and = with ==. Difficulty is when real error occurred long before the error was detected.
Include productions for common errors
.
Change the input I to the closest
correct input I' and
produce the parse tree for I'.
I don't use these without saying so.
This is mostly (very useful) notation.
Assume we have a production A → α.
We would then say that A derives α and write
A ⇒ α
We generalize this.
If, in addition, β and γ are strings, we say that
βAγ derives βαγ and write
βAγ ⇒ βαγ
We generalize further.
If x derives y and y derives z, we say x derives z and write
x ⇒* z.
The notation used is ⇒ with a * over it (I don't see it in
html).
This should be read derives in zero or more steps
.
Formally,
Definition: If S is the start symbol and S ⇒* x, we say x is a sentential form of the grammar.
A sentential form may contain nonterminals and terminals. If it contains only terminals it is a sentence of the grammar and the language generated by a grammar G, written L(G), is the set of sentences.
Definition: A language generated by a (context-free) grammar is called a context free language.
Definition: Two grammars generating the same language are called equivalent.
Examples: Recall the ambiguous grammar above
E → E + E | E * E | ( E ) | id
We see that id + id is a sentence.
Indeed it can be derived in two ways from the start symbol E
E ⇒ E + E ⇒ id + E ⇒ id + id
E ⇒ E + E ⇒ E + id ⇒ id + id
In the first derivation, we replaced the leftmost nonterminal by the body of a production having the nonterminal as head. This is called a leftmost derivation. Similarly the second derivation in which the rightmost nonterminal is replaced is called a rightmost derivation or a canonical derivation.
When one wishes to emphasize that a (one step) derivation is leftmost they write an lm under the ⇒. To emphasize that a (general) derivation is leftmost, one writes an lm under the ⇒*. Similarly one writes rm to indicate that a derivation is rightmost. I won't do this in the notes but will on the board.
Definition: If x can be derived using a leftmost derivation, we call x a left-sentential form. Similarly for right-sentential form.
Homework: 4.1 a, c, d
The leaves of a parse tree (or of any other tree), when read left to right, are called the frontier of the tree. For a parse tree we also call them the yield of the tree.
If you are given a derivation starting with a single nonterminal,
A ⇒ x1 ⇒ x2 ... ⇒ xn
it is easy to write a parse tree with A as the root and
xn as the leaves.
Just do what (the productions contained in) each step of the
derivation says.
The LHS of each production is a nonterminal in the frontier of the
current tree so replace it with the RHS to get the next tree.
Do this for both the leftmost and rightmost derivations of id+id above.
So there can be many derivations that wind up with the same final tree.
But for any parse tree there is a unique leftmost derivation the produces that tree and a unique rightmost derivation that produces the tree. There may be others as well (e.g., sometime choose the leftmost nonterminal to expand; other times choose the rightmost).
Homework: 4.1 b
Recall that an ambiguous grammar is one for which there is more than one parse tree for a single sentence. Since each parse tree corresponds to exactly one leftmost (or rightmost) derivation, an ambiguous grammar is one for which there is more than one leftmost (or rightmost) derivation of a given sentence.
We know that the grammar
E → E + E | E * E | ( E ) | id
is ambiguous because we have seen (a few lectures ago) two parse
trees for
E ⇒ E + E E ⇒ E * E
⇒ id + E ⇒ E + E * E
⇒ id + E * E ⇒ id + E * E
⇒ id + id * E ⇒ id + id * E
⇒ id + id * id ⇒ id + id * E
As we stated before we prefer unambiguous grammars. Failing that, we want disambiguation rules.
Skipped
Alternatively context-free languages vs regular languages.
Given an RE, construct an NFA as in chapter 3.
From that NFA construct a grammar as follows.
If you trace an NFA accepting a sentence, it just corresponds to the constructed grammar deriving the same sentence. Similarly, follow a derivation and notice that at any point prior to acceptance there is only one nonterminal; this nonterminal gives the state in the NFA corresponding to this point in the derivation.
The book starts with (a|b)*abb and then uses the short NFA on the left below. Recall that the NFA generated by our construction is the longer one on the right.


The book gives the simple grammar for the short diagram.
Let's be ambitious and try the long diagram
A0 → A1 | A7
A1 → A2 | A4
A2 → a A3
A3 → A6
A4 → b A5
A5 → A6
A6 → A1 | A7
A7 → a A8
A8 → b A9
A9 → b A10
A10 → ε
Now trace a path in the NFA and see that it is just a derivation. The same is true in reverse (derivation gives path). The key is that at every stage you have only one nonterminal.
The grammar
A → a A b | ε
generates all strings of the form anbn, where
there are the same number of a's and b's.
In a sense the grammar has counted.
No RE can generate this language (proof in book).
Why have separate lexer and parser?
Recall the ambiguous grammar with the notorious dangling
else
problem.
stmt → if expr then stmt
| if expr then stmt else stmt
| other
This has two leftmost derivations for
if E1 then S1 else if E2 then S2 else S3
Do these on the board. They differ in the beginning.
In this case we can find a non-ambiguous, equivalent grammar.
stmt → matched-stmt | open-stmt
matched-stmp → if expr then matched-stmt else matched-stmt
| other
open-stmt → if expr then stmt
| if expr then matched-stmt else open-stmt
On the board try to find leftmost derivations of the problem sentence above.
We did special cases in chapter 2.
Now we do it right
(tm).
Previously we did it separately for one production and for two productions with the same nonterminal A on the LHS. Not surprisingly, this can be done for n such productions (together with other non-left recursive productions involving A).
Specifically we start with
A → A x1 | A x2 | ... A xn | y1 | y2 | ... ym
where the x's and y's are strings, no x is ε, and no y
begins with A.
The equivalent non-left recursive grammar is
A → y1 A' | ... | ym A'
A' → x1 A' | ... | xn A' | ε
Example: Assume x1 is + and y1 is *.
With the recursive grammar, we have the following lm derivation.
A ⇒ A + ⇒ , +
With the non-recursive grammar we have
A ⇒ , A' ⇒ , + A' ⇒ , +
This removes direct left recursion where a production with A on the left hand side begins with A on the right. If you also had direct left recursion with B, you would apply the procedure twice.
The harder general case is where you permit indirect left recursion, where, for example one production has A as the LHS and begins with B on the RHS, and a second production has B on the LHS and begins with A on the RHS. Thus in two steps we can turn A into something starting again with A. Naturally, this indirection can involve more than 2 nonterminals.
Theorem: All left recursion can be eliminated.
Proof: The book proves this for grammars that have
no ε-productions and no cycles
and has exercises
asking the reader to prove that cycles and ε-productions can
be eliminated.
We will try to avoid these hard cases.
Homework: Eliminate left recursion in the
following grammar for simple postfix expressions.
X → S S + | S S * | a
If two productions with the same LHS have their RHS beginning with the same symbol, then the FIRST sets will not be disjoint so predictive parsing (chapter 2) will be impossible and more generally top down parsing (later this chapter) will be more difficult as a longer lookahead will be needed to decide which production to use.
So convert A → x y1 | x y2 into
A → x A'
A' → y1 | y2
In other words factor outthe x.
Homework: Left factor your answer to the previous homework.
Although our grammars are powerful, they are not all-powerful. For example, we cannot write a grammar that checks that all variables are declared before used.
We did an example of top down parsing, namely predictive parsing, in chapter 2.
For top down parsing, we
The above has two nondeterministic choices (the nonterminal, and the production) and requires luck at the end. Indeed, the procedure will generate the entire language. So we have to be really lucky to get the input string.
Let's reduce the nondeterminism in the above algorithm by specifying which nonterminal to expand. Specifically, we do a depth-first (left to right) expansion.
We leave the choice of production nondeterministic.
We also process the terminals in the RHS, checking that they match the input. By doing the expansion depth-first, left to right, we ensure that we encounter the terminals in the order they will appear in the frontier of the final tree. Thus if the terminal does not match the corresponding input symbol now, it never will and the expansion so far will not produce the input string as desired.
Now our algorithm is
for i = 1 to n
if Xi is a nonterminal
process Xi // recursive
else if Xi (a terminal) matches current input symbol
advance input to next symbol
else // trouble Xi doesn't match and never will
Note that the trouble
mentioned at the end of the algorithm
does not signify an erroneous input.
We may simply have chosen the wrong
production in step 2.
In a general recursive descent (top-down) parser, we would support backtracking, that is when we hit the trouble, we would go back and choose another production. Since this is recursive, it is possible that no productions work for this nonterminal, because the wrong choice was made earlier.
The good news is that we will work with grammars where we can control the nondeterminism much better. Recall that for predictive parsing, the use of 1 symbol of lookahead made the algorithm fully deterministic, without backtracking.
We used FIRST(RHS) when we did predictive parsing.
Now we learn the whole truth about these two sets, which prove to be quite useful for several parsing techniques (and for error recovery).
The basic idea is that FIRST(α) tells you what the first symbol can be when you fully expand the string α and FOLLOW(A) tells what terminals can immediately follow the nonterminal A.
Definition: For any string α of grammar symbols, we define FIRST(α) to be the set of terminals that occur as the first symbol in a string derived from α. So, if α⇒*xQ for x a terminal and Q a string, then x is in FIRST(α). In addition if α⇒*ε, then ε is in FIRST(α).
Definition: For any nonterminal A, FOLLOW(A) is the set of terminals x, that can appear immediately to the right of A in a sentential form. Formally, it is the set of terminals x, such that S⇒*αAxβ. In addition, if A can be the rightmost symbol in a sentential form, the endmarker $ is in FOLLOW(A).
Note that there might have been symbols between A and x during the derivation, providing they all derived ε and eventually x immediately follows A.
Unfortunately, the algorithms for computing FIRST and FOLLOW are not as simple to state as the definition suggests, in large part caused by ε-productions.
Do the FIRST and FOLLOW sets for
E → T E'
E' → + T E' | ε
T → F T'
T' → * F T' | ε
F → ( E ) | id
Homework: Compute FIRST and FOLLOW for the postfix grammar S → S S + | S S * | a
The predictive parsers of chapter 2 are recursive descent parsers needing no backtracking. A predictive parser can be constructed for any grammar in the class LL(1). The two Ls stand for (processing the input) Left to right and for producing Leftmost derivations. The 1 in parens indicates that 1 symbol of lookahead is used.
Definition: A grammar is LL(1) if for all production pairs A → α | β
The 2nd condition may seem strange; it did to me for a while. Let's consider the simplest case that condition 2 is trying to avoid.
S → A b // b is in FOLLOW(A)
A → b // α=b so α derives a string beginning with b
A → ε // β=ε so β derives ε
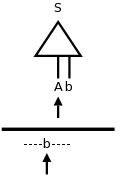
Assume we are using predictive parsing and, as illustrated in the diagram to the right, we are at A in the parse tree and b in the input. Since lookahead=b and b is in FIRST(RHS) for the top A production, we would choose that production to expand A. But this could be wrong! Remember that we don't look ahead in the tree just in the input. So we would not have noticed that the next node in the tree (i.e., in the frontier) is b. This is possible since b is in FOLLOW(A). So perhaps we should use the second A production to produce ε in the tree, and then the next node b would match the input b.
The goal is to produce a table telling us at each situation which
production to apply.
A situation
means a nonterminal in the parse tree and an
input symbol in lookahead.
So we produce a table with rows corresponding to nonterminals and columns corresponding to input symbols (including $. the endmarker). In an entry we put the production to apply when we are in that situation.
We start with an empty table M and populate it as follows. (2nd edition has typo, A instead of α.) For each production A → α
strange) condition above. If ε is in FIRST(α), then α⇒*ε. Hence we should apply the production A→α, have the α go to ε and then the b (or $), which follows A will match the b in the input.
When we have finished filling in the table M, what do we do if an slot has
LL(1) grammarsSomeone erred when they said the grammar generated an LL(1) language. Since the language is not LL(1), we must use a different technique. One possibility is to use bottom-up parsing, which we study next. Another is to modify the procedure for this non-terminal to look further ahead (typically one more token) to decide what action to perform.
Example: Work out the parsing table for
E → T E'
E' → + T E' | ε
T → F T'
T' → * F T' | ε
F → ( E ) | id
| FIRST | FOLLOW | |
|---|---|---|
| E | ( id | $ ) |
| E' | ε + | $ ) |
| T | ( id | + $ ) |
| T' | ε * | + $ ) |
| F | ( id | * + $ ) |
We already computed FIRST and FOLLOW as shown on the right. The table skeleton is
| Nonter- minal | Input Symbol | |||||
|---|---|---|---|---|---|---|
| + | * | ( | ) | id | $ | |
| E | ||||||
| E' | ||||||
| T | ||||||
| T' | ||||||
| F | ||||||
Homework: Produce the predictive parsing table for
This illustrates the standard technique for eliminating recursion by keeping the stack explicitly. The runtime improvement can be considerable.
Skipped.

Now we start with the input string, i.e., the bottom (leaves) of what will become the parse tree, and work our way up to the start symbol.
For bottom up parsing, we are not as fearful of left recursion as we were with top down. Our first few examples will use the left recursive expression grammar
E → E + T | T
T → T * F | F
F → ( E ) | id
Remember that running a production in reverse
, i.e., replacing
the RHS by the LHS is called reducing.
So our goal is to reduce the input string to the start symbol.
On the right is a movie of parsing id*id in a bottom-up fashion. Note the way it is written. For example, from step 1 to 2, we don't just put F above id*id. We draw it as we do because it is the current top of the tree (really forest) and not the bottom that we are working on so we want the top to be in horizontal line and hence easy to read.
The tops of the forest are the roots of the subtrees present in the
diagram.
For the movie those are
id * id, F * id, T * F, T, E
Note that (since the reduction successfully reaches the start
symbol) each of these sets of roots is a sentential form.
The steps from one frame of the movie, when viewed going down the
page, are reductions (replace the RHS of a production by the LHS).
Naturally, when viewed going up the page, we have a derivation
(replace LHS by RHS).
For our example the derivation is
E ⇒ T ⇒ T * F ⇒
T * id ⇒ F * id ⇒ id * id
Note that this is a rightmost derivation and hence each of the sets of roots identified above is a right sentential form. So the reduction we did in the movie was a rightmost derivation in reverse.
Remember that for a non-ambiguous grammar there is only one rightmost derivation and hence there is only one rightmost derivation in reverse.
Remark: You cannot simply scan the string (the
roots of the forest) from left to right and choose the first
substring that matches the RHS of some production.
If you try it in our movie you will reduce T to E right after T
appears.
The result is not a right sentential form.
| Right Sentential Form | Handle | Reducing Production |
|---|---|---|
| id1 * id2 | id1 | F → id |
| F * id2 | F | T → F |
| T * id2 | id2 | F → id |
| T * F | T * F | E → T * F |
The strings that are reduced during the reverse of a rightmost derivation are called the handles. For our example, this is shown in the table on the right.
Note that the string to the right of the handle must contain only terminals. If there was a non-terminal to the right, it would have been reduced in the RIGHTmost derivation that leads to this right sentential form.
Often instead of referring to a derivation A→α as a handle, we call α the handle. I should say a handle because there can be more than one if the grammar is ambiguous.
So (assuming a non-ambiguous grammar) the rightmost derivation in reverse can be obtained by constantly reducing the handle in the current string.
Homework: 4.23 a c
We use two data structures for these parsers.
shifted(see below) onto the stack will be terminals, but some are
reducedto nonterminals. The bottom of the stack is marked with $ and initially the stack is empty (i.e., has just $).
| Stack | Input | Action |
|---|---|---|
| $ | id1*id2$ | shift |
| $id1 | *id2$ | reduce F→id |
| $F | *id2$ | reduce T→F |
| $T | *id2$ | shift |
| $T* | id2$ | shift |
| $T*id2 | $ | reduce F→id |
| $T*F | $ | reduce T→T*F |
| $T | $ | reduce E→T |
| $E | $ | accept |
A technical point, which explains the usage of a stack is that a handle is always at the TOS. See the book for a proof; the idea is to look at what rightmost derivations can do (specifically two consecutive productions) and then trace back what the parser will do since it does the reverse operations (reductions) in the reverse order.
We have not yet discussed how to decide whether to shift or reduce when both are possible. We have also not discussed which reduction to choose if multiple reductions are possible. These are crucial question for bottom up (shift-reduce) parsing and will be addressed.
Homework: 4.23 b
There are grammars (non-LR) for which no viable algorithm can decide whether to shift or reduce when both are possible or which reduction to perform when several are possible. However, for most languages, choosing a good lexer yields an LR(k) language of tokens. For example, ada uses () for both function calls and array references. If the lexer returned id for both array names and procedure names then a reduce/reduce conflict would occur when the stack was ... id ( id and the input ) ... since the id on TOS should be reduced to parameter if the first id was a procedure name and to expr if the first id was an array name. A better lexer (and an assumption, which is true in ada, that the declaration must precede the use) would return proc-id when it encounters a lexeme corresponding to a procedure name. It does this by constructing the symbol table it builds.
Remark: Both editions do a warm up
before
getting down to business with full LR parsing.
The first edition does operator precedence and covers SLR in the
middle of the section on LR parsing.
The second omits operator precedence and does SLR here.
I am following the second since operator precedence is no longer
widely used and I believe SLR will be more helpful
when trying to understand full LR and hence serves as a better
introduction the subject.
Indeed, I will have much more to say about SLR than the other LR schemes. The reason is that SLR is simpler to understand, but does capture the essence of shift-reduce, bottom-up parsing. The disadvantage of SLR is that there are LR grammars that are not SLR.
I will just say the following about operator precedence. We shall see that a major consideration in all the bottom-up, shift-reduce parsers is deciding when to shift and when to reduct. Consider parsing A+B*C in C/java/etc. When the stack is A+B and the remaining input is *C, the parser needs to know whether to reduce A+B or shift in * and then C. (Really the A+B will probably by now be more like E+T.) The idea of operator precedence is that we give * higher precedence so when the parser see * on the input it knows not to reduce +. More details are in the first (i.e., your) edition of the text.
The text's presentation is somewhat controversial.
Most commercial compilers use hand-written top-down parsers of the
recursive-descent (LL not LR) variety.
Since the grammars for these languages are not LL(1), the
straightforward application of the techniques we have seen will not
work.
Instead the parsers actually look ahead further than one token, but
only at those few places where the grammar is in fact not LL(1).
Recall that (hand written) recursive descent compilers have a
procedure for each nonterminal so we can customize as needed
.
These compiler writers claim that they are able to produce much
better error messages than can readily be obtained by going to LR
(with its attendant requirement that a parser-generator be used since
the parsers are too large to construct by hand).
Note that compiler error messages is a very important user interface
issue and that with recursive descent one can augment the procedure
for a nonterminal with statements like
if (nextToken == X) then error(expected Y here
)
Nonetheless, the claims made by the text are correct, namely.
We now come to grips with the big question
:
How does a shift-reduce parser know when to shift and when to
reduce?
This will take a while to answer in a satisfactory manner.
The unsatisfactory answer is that the parser has tables that say in
each situation
whether to shift or reduce (or announce error,
or announce acceptance).
To begin the path toward the answer, we need several definitions.
An item is a production with a marker saying how far the parser has gotten with this production. Formally,
Definition: An (LR(0)) item of a grammar is a production with a dot added somewhere to the RHS.
Examples:
The item E → E · + T signifies that the parser has just processed input that is derivable from E and will look for input derivable from + T.
Line 4 indicates that the parser has just seen the entire
RHS and must consider reducing it to E.
Important: consider
does not mean do
.
The parser groups certain items together into states. As we shall see, the items with a given state are treated similarly.
Our goal is to construct first the canonical LR(0)
collection of states and then a DFA called the LR(0) automaton
(technically not a DFA since no dead state
).
To construct the canonical LR(0) collection formally and present the parsing algorithm in detail we shall
Augmenting the grammar is easy. We simply add a new start state S' and one production S'→S. The purpose is to detect success, which occurs when the parser is ready to reduce S to S'.
So our example grammar
E → E + T | T
T → T * F | F
F → ( E ) | id
is augmented by adding the production E' → E.
I hope the following interlude will prove helpful. In preparing to present SLR, I was struck how it looked like we were working with a DFA that came from some (unspecified and unmentioned) NFA. It seemed that by first doing the NFA, I could give some rough insight. Since for our current example the NFA has more states and hence a bigger diagram, let's consider the following extremely simple grammar.
E → E + T
E → T
T → id
When augmented this becomes
E' → E
E → E + T
E → T
T → id
When the dots are added we get 10 items (4 from the second
production, 2 each from the other three).
See the diagram at the right.
We begin at E'→.E since it is the start item.
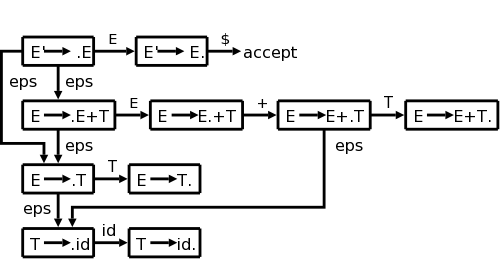
Note that there are really four kinds
of edges.
If we were at the item E→E·+T (the dot indicating that we have seen an E and now need a +) and shifted a + from the input to the stack we would move to the item E→E+·T. If the dot is before a non-terminal, the parser needs a reduction with that non-terminal as the LHS.
Now we come to the idea of closure, which I illustrate in the diagram with the ε's. Please note that this is rough, we are not doing regular expressions again, but I hope this will help you understand the idea of closure, which like ε in regular production leads to nondeterminism.
Look at the start state. The placement of the dot indicates that we next need to see an E. Since E is a nonterminal, we won't see it in the input, but will instead have to generate it via a production. Thus by looking for an E, we are also looking for any production that has E on the LHS. This is indicated by the two ε's leaving the top left box. Similarly, there are ε's leaving the other three boxes where the dot is immediately to the left of a nonterminal.
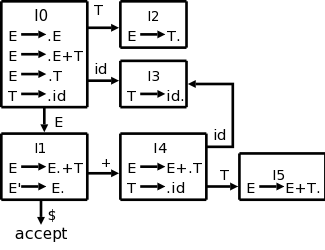 As with regular expressions, we combine
As with regular expressions, we combine n-items
connected by
an ε arc into a d-item
.
The actual terminology used is that we combine these items into a
set of items (later referred to as a state).
There is another combination that occurs.
The top two n-items in the left column are combined into the same
d-item and both n-items have E transitions (outgoing arcs labeled
E).
Since we are considering these two n-items to be the same d-item and
the arcs correspond to the same transition, the two targets (the
top two n-items in the 2nd column) are combined.
A d-item has all the outgoing arcs of the original n-items
it contains.
This is the way we converted an NFAs into a DFA in the previous chapter.
I0, I1, etc are called (LR(0)) item sets, and
the collection with the arcs (i.e., the DFA) is called the LR(0)
automaton.
| Stack | Symbols | Input | Action |
|---|---|---|---|
| 0 | id+id$ | Shift to 3 | |
| 03 | id | +id$ | Reduce by T→id |
| 02 | T | +id$ | Reduce by E→T. |
| 01 | E | +id$ | Shift to 4 |
| 014 | E+ | id$ | Shift to 3 |
| 0143 | E+id | $ | Reduce by T→id |
| 0145 | E+T | $ | Reduce by E→E+T |
| 01 | E | $ | Accept |
We start in the initial state with the stack empty and the input full. The $'s are just end markers. From state 0, called I0 in my diagram (following the book they are called I's since they are sets of items), we can only shift in the id (the nonterminals will appear in the symbols column). This brings us to I3 so we push a 3 onto the stack
In I3 we see a completed production in the box (the
dot is on the extreme right).
Thus we can reduce by this production.
To reduce we pop the stack for each symbol in the RHS since we are
replacing the RHS by the LHS; this time the RHS has one symbol so we
pop the stack once and also remove one symbol.
The stack corresponds to moves so we are undoing the move to 3 and
we are temporarily
in 0 again.
But the production has a T on the LHS so we follow the T production
from 0 to 2, push T onto Symbols, and push 2 onto the stack.
In I2 we again see a completed production and do another reduction, which brings us to 1.
The next two steps are shifts of + and id.
We then reduce the id to T and are in step 5 ready for the
big one
.
The reduction in 5 has three symbols on the RHS so we pop (back up) three times again temporarily landing in 0, but the RHS puts us in 1.
Perfect! We have just E as a symbol and the input is empty so we are ready to reduce by E'→E, which signifies acceptance.
Now we rejoin the book and say it more formally.
Say I is a set of items and one of these items is A→α·Bβ. This item represents the parser having seen α and records that the parser might soon see the remainder of the RHS. For that to happen the parser must first see a string derivable from B. Now consider any production starting with B, say B→γ. If the parser is to making progress on A→α·Bβ, it will need to be making progress on one such B→·γ. Hence we want to add all the latter productions to any state that contains the former. We formalize this into the notion of closure.
Definition: For any set of items I, CLOSURE(I) is formed as follows.
Example: Recall our main example
E' → E
E → E + T | T
T → T * F | F
F → ( E ) | id
CLOSURE({E' → E})
contains 7 elements.
The 6 new elements are the 6 original productions each with a dot
right after the arrow.
If X is a grammar symbol, then moving from A→α·Xβ to A→αX·β signifies that the parser has just processed (input derivable from) X. The parser was in the former position and X was on the input; this caused the parser to go to the latter position. We (almost) indicate this by writing GOTO(A→α·Xβ,X) is A→αX·β. I said almost because GOTO is actually defined from item sets to item sets not from items to items.
Definition: If I is an item set and X is a grammar symbol, then GOTO(I,X) is the closure of the set of items A→αX·β where A→α·Xβ is in I.
I really believe this is very clear, but I understand that the formalism makes it seem confusing. Let me begin with the idea.
We augment the grammar and get this one new production; take its closure. That is the first element of the collection; call it Z. Try GOTOing from Z, i.e., for each grammar symbol, consider GOTO(Z,X); each of these (almost) is another element of the collection. Now try GOTOing from each of these new elements of the collection, etc. Start with jane smith, add all her friends F, then add the friends of everyone in F, called FF, then add all the friends of everyone in FF, etc
The (almost)
is because GOTO(Z,X) could be empty so formally
we construct the canonical collection of LR(0) items, C, as follows
This GOTO gives exactly the arcs in the DFA I constructed earlier. The formal treatment does not include the NFA, but works with the DFA from the beginning.
Homework:
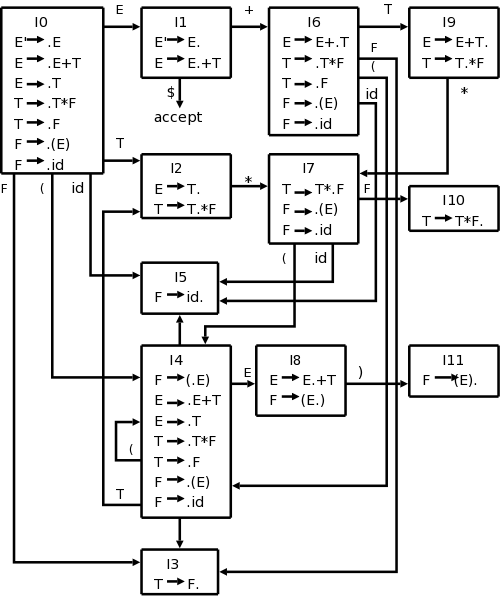
Our main example is larger than the toy I did before. The NFA would have 2+4+2+4+2+4+2=20 states (a production with k symbols on the RHS gives k+1 N-states since there k+1 places to place the dot). This gives rise to 11 D-states. However, the development in the book, which we are following now, constructs the DFA directly. The resulting diagram is on the right.
Start constructing the diagram on the board. Begin with {E' → ·E}, take the closure, and then keep applying GOTO.
The LR-parsing algorithm must decide when to shift and when to reduce (and in the latter case, by which production). It does this by consulting two tables, ACTION and GOTO. The basic algorithm is the same for all LR parsers, what changes are the tables ACTION and GOTO.
We have already seen GOTO (for SLR).
Technical point that may, and probably should, be ignored: our GOTO was defined on pairs [item-set,grammar-symbol]. The new GOTO is defined on pairs [state,nonterminal]. A state (except the initial state) is an item set together with the grammar symbol that was used to generate it (via the old GOTO). We will not use the new GOTO on terminals so we just define it on nonterminals.
Given a state i and a terminal a (or the endmarker), ACTION[i,a] can be
So ACTION is the key to deciding shift vs. reduce. We will soon see how this table is computed for SLR.
Since ACTION is defined on [state,terminal] pairs and GOTO is defined on [state,nonterminal], we can combine these tables into one defined on [state,grammar-symbol] pairs.
This formalism is useful for stating the actions of the parser precisely, but I believe it can be explained without it.
As mentioned above the Symbols column is redundant so a configuration of the parser consists of the current stack and the remainder of the input. Formally it is
The parser consults the combined ACTION-GOTO table for its current state (TOS) and next input symbol, formally this is ACTION[sm,ai], and proceeds as follows based on the value in the table. We have done this informally just above; here we use the formal treatment
The missing piece of the puzzle is finally revealed.
The book (both editions) and the rest of the world seem to use GOTO for both the function defined on item sets and the derived function on states. As a result we will be defining GOTO in terms of GOTO. (I notice that the first edition uses goto for both; I have been following the second edition, which uses GOTO. I don't think this is a real problem.) Item sets are denoted by I or Ij, etc. States are denoted by s or si or (get ready) i. Indeed both books use i in this section. The advantage is that on the stack we placed integers (i.e., i's) so this is consistent. The disadvantage is that we are defining GOTO(i,A) in terms of GOTO(Ii,A), which looks confusing. Actually, we view the old GOTO as a function and the new one as an array (mathematically, they are the same) so we actually write GOTO(i,A) and GOTO[Ii,A].
We start with an augmented grammar (i.e., we added S' → S).
shift j, where GOTO(Ii,b)=Ij.
reduce A→α.
accept.
error.
| State | ACTION | GOTO | |||||||
|---|---|---|---|---|---|---|---|---|---|
| id | + | * | ( | ) | $ | E | T | F | |
| 0 | s5 | s4 | 1 | 2 | 3 | ||||
| 1 | s6 | acc | |||||||
| 2 | r2 | s7 | r2 | r2 | |||||
| 3 | r4 | r4 | r4 | r4 | |||||
| 4 | s5 | s4 | 8 | 2 | 3 | ||||
| 5 | r6 | r6 | r6 | r6 | |||||
| 6 | s5 | s4 | 9 | 3 | |||||
| 7 | s5 | s4 | 10 | ||||||
| 8 | s6 | s11 | |||||||
| 9 | r1 | s7 | r1 | r1 | |||||
| 10 | r3 | r3 | r3 | r3 | |||||
| 11 | r5 | r5 | r5 | r5 | |||||
shift and go to state 5.
reduce by production number 2, where we have numbered the productions as follows.
The shift actions can be read directly off the DFA. For example I1 with a + goes to I6, I6 with an id goes to I5, and I9 with a * goes to I7.
The reduce actions require FOLLOW.
Consider I5={F→id·}.
Since the dot is at the end, we are ready to reduce, but we must
check if the next symbol can follow the F we are reducing to.
Since FOLLOW(F)={+,*,),$}, in row 5 (for I5) we put
r6 (for reduce by production 6
) in the columns for
+, *, ), and $.
The GOTO columns can also be read directly off the DFA. Since there is an E-transition (arc labeled E) from I0 to I1, the column labeled E in row 0 contains a 1.
Since the column labeled + is blank for row 7, we see that it would be an error if we arrived in state 7 when the next input character is +.
Finally, if we are in state 1 when the input is exhausted ($ is the next input character), then we have a successfully parsed the input.
| Stack | Symbols | Input | Action |
|---|---|---|---|
| 0 | id*id+id$ | shift | |
| 05 | id | *id+id$ | reduce by F→id |
| 03 | F | *id+id$ | reduct by T→id |
| 02 | T | *id+id$ | shift |
| 027 | T* | id+id$ | shift |
| 0275 | T*id | +id$ | reduce by F→id |
| 027 10 | T*F | +id$ | reduce by T→T*F |
| 02 | T | +id$ | reduce by E→T |
| 01 | E | +id$ | shift |
| 016 | E+ | id$ | shift |
| 0165 | E+id | $ | reduce by F→id |
| 0163 | E+F | $ | reduce by T→F |
| 0169 | E+T | $ | reduce by E→E+T |
| 01 | E | $ | accept |
Homework:
Construct the SLR parsing table for the
following grammar
X → S S + | S S * | a
You already constructed the LR(0) automaton for this example in
the previous homework.
Skipped.
We consider very briefly two alternatives to SLR, canonical-LR or LR, and lookahead-LR or LALR.
SLR used the LR(0) items, that is the items used were productions with an embedded dot, but contained no other (lookahead) information. The LR(1) items contain the same productions with embedded dots, but add a second component, which is a terminal (or $). This second component becomes important only when the dot is at the extreme right (indicating that a reduction can be made if the input symbol is in the appropriate FOLLOW set). For LR(1) we do that reduction only if the input symbol is exactly the second component of the item. This finer control of when to perform reductions, enables the parsing of a larger class of languages.
Skipped.
Skipped.
For LALR we merge various LR(1) item sets together, obtaining nearly the LR(0) item sets we used in SLR. LR(1) items have two components, the first, called the core, is a production with a dot; the second a terminal. For LALR we merge all the item sets that have the same cores by combining the 2nd components (thus permitting reductions when any of these terminals is the next input symbol). Thus we obtain the same number of states (item sets) as in SLR since only the cores distinguish item sets.
Unlike SLR, we limit reductions to occurring only for certain specified input symbols. LR(1) gives finer control; it is possible for the LALR merger to have reduce-reduce conflicts when the LR(1) items on which it is based is conflict free.
Although these conflicts are possible, they are rare and the size reduction from LR(1) to LALR is quite large. LALR is the current method of choice for bottom-up, shift-reduce parsing.
Skipped.
Skipped.
Skipped.
Dangling-ElseAmbiguity
Skipped.
Skipped.
The tool corresponding to Lex for parsing is yacc, which (at least originally) stood for yet another compiler compiler. This name is cute but somewhat misleading since yacc (like the previous compiler compilers) does not produce a compiler, just a parser.
The structure of the user input is similar to that for lex, but instead of regular definitions, one includes productions with semantic actions.
There are ways to specify associativity and precedence of operators. It is not done with multiple grammar symbols as in a pure parser, but more like declarations.
Use of Yacc requires a serious session with its manual.
Skipped.
Skipped
Skipped
Homework: Read Chapter 5.
Again we are redoing, more formally and completely, things we briefly discussed when breezing over chapter 2.
Recall that a syntax-directed definition (SDD) adds semantic rules
to the productions of a grammar.
For example to the production T → T1 / F we might add the rule
T.code = T1.code || F.code || '/'
if we were doing an infix to postfix translator.
Rather than constantly copying ever larger strings to finally
output at the root of the tree after a depth first traversal, we can
perform the output incrementally by embedding semantic actions
within the productions themselves.
The above example becomes
T → T1 / F { print '/' }
Since we are generating postfix, the action comes at the end (after
we have generated the subtrees for T1 and F, and hence
performed their actions).
In general the actions occur within the production, not necessarily
after the last symbol.
For SDD's we conceptually need to have the entire tree available after the parse so that we can run the depth first traversal. (It is depth first since we are doing postfix; we will see other orders shortly.) Semantic actions can be performed during the parse, without saving the tree.
Formally, attributes are values (of any type) that are associated with grammar symbols. Write X.a for the attribute a of symbol X. You can think of attributes as fields in a record/struct/object.
Semantic rules (rules for short) are associated with productions.
Terminals can have synthesized attributes, that are given to it by the lexer (not the parser). There are no rules in an SDD giving values to attributes for terminals. Terminals do not have inherited attributes. A nonterminal A can have both inherited and synthesized attributes. The difference is how they are computed by rules associated with a production at a node N of the parse tree. We sometimes refer to the production at node N as production N.
The arithmetic division example above was synthesized.
| Production | Semantic Rules |
|---|---|
| L → E $ | L.val = E.val |
| E → E1 + T | E.val = E1.val + T.val |
| E → E1 - T | E.val = E1.val - T.val |
| E → T | E.val = T.val |
| T → T1 * F | T.val = T1.val * F.val |
| T → T1 / F | T.val = T1.val / F.val |
| T → F | T.val = F.val |
| F → ( E ) | F.val = E.val |
| F → num | F.val = num.lexval |
Example: The SDD at the right gives a left-recursive grammar for expressions with an extra nonterminal L added as the start symbol. The terminal num is given a value by the lexer, which corresponds to the value stored in the numbers table for lab 2.
Draw the parse tree for 7+6/3 on the board and verify that L.val is 9, the value of the expression.
Definition: This example use only synthesized attributes; such SDDs are called S-attributed and have the property that the rules give the attribute of the LHS in terms of attributes of the RHS.
Inherited attributes are more complicated since the node N of the parse tree with which it is associated (which is also the natural node to store the value) does not contain the production with the corresponding semantic rule.
Definition: An inherited attribute of a nonterminal B at node N (where B is the LHS) is defined by a semantic rule of the production at the parent of N (where B occurs in the RHS). The value depends only on attributes at N, N's siblings, and N's parent.
Note that when viewed from the parent node P (the site of the semantic rule), the inherited attribute depends on values at P and at P's children (the same as for synthesized attributes). However, and this is crucial, the nonterminal B is the LHS of a child of P and hence the attribute is naturally associated with that child. It is possibly stored there and is shown there in the diagrams below.
We will see an example with inherited attributes soon.
Definition:Often the attributes are just evaluations without side effects. In such cases we call the SDD an attribute grammar.
Remark: There was a question last time about SLR concerning B⇒*ε. Consider A→α·Bβ. Can we consider the dot to be on the other side of B since B derives ε? I said I thought not and want to add that, since B derives ε, these productions will appear in the LR(0) automaton and hence will be taken care of without any extra rules here.
Remark: Do 7+6/3 on board using the SDD from the end of the previous lecture (should have been done last time).
If we are given an SDD and a parse tree for a given sentence, we would like to evaluate the annotations at every node. Since, for synthesized annotations parents can depend on children, and for inherited annotations children can depend on parents, there is no guarantee that one can in fact find an order of evaluation. The simplest counterexample is the single production A→B with synthesized attribute A.syn, inherited attribute B.inh, and rules A.syn=B.inh and B.inh=A.syn+1. This means to evaluate A.syn at the parent node we need B.inh at the child and vice versa. Even worse it is very hard to tell, in general, if every sentence has a successful evaluation order.
All this not withstanding we will not have great difficulty because we will not be considering the general case.
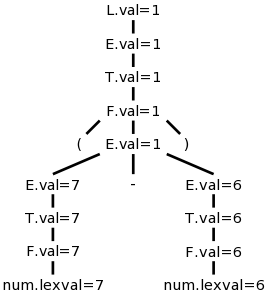
Recall that a parse tree has leaves that are terminals and internal
nodes that are non-terminals.
We when we decorate the parse tree with attributes, the result is
called an annotated parse tree, which is constructed as
follows.
Each internal node corresponds to a production with the symbol
labeling the node the LHS of the production.
If there are no attributes for the LHS in this production, we leave
the node as it was (I don't believe this is a common occurrence).
If there are k attributes for the LHS, we replace the LHS in the
parse tree by k equations.
The LHS of the equation is the attribute and the right hand side is
its value.
Note that the annotated parse tree contains all the information of
the original parse tree since we replaced something like E with
something like E.att=7
.
We computed the values to put in this tree for 7+6/3 and on the right is (7-6).
Homework: 5.1
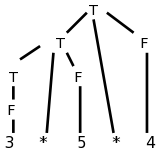
Consider the following left-recursive grammar for multiplication of numbers and the parse tree on the right for 3*5*4.
T → T * F T → F F → num
It is easy to see how the values can be propagated up the tree and the expression evaluated.
When doing top-down parsing, we need to avoid left recursion.
Consider the grammar below, which is the result of removing
the left recursion, and again its parse tree is shown on the right.
Try not to look at the semantic rules for the moment.
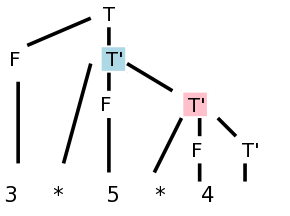
| Production | Semantic Rules | Type |
|---|---|---|
| T → F T' | T'.lval = F.val | Inherited |
| T.val = T'.tval | Synthesized | |
| T' → * F T1' | T'1.lval = T'.lval * F.val | Inherited |
| T'.tval = T'1.tval | Synthesized | |
| T' → ε | T'.tval = T'.lval | Synthesized |
| F → num | F.val = num.lexval | Synthesized |
Now where on the tree should we do the multiplication 3*5? There is no node that has 3 and * and 5 as children. The second production is the one with the * so that is the natural candidate for the multiplication site. Make sure you see that this production (for 3*5) is associated with the blue highlighted node in the parse tree. The right operand (5) can be obtained from the F that is the middle child of this T'. F gets the value from its child, the number itself; this is an example of the simple synthesized case we have already seen, F.val=num.lexval (see the last semantic rule in the table).
But where is the left operand?
It is located at the sibling of T' in the parse tree, i.e., at the F
immediately to T's left.
This F is not mentioned in the production associated with the
T' node we are examining.
So, how does T' get F.val from its sibling?
The common parent, in this case T, can get the value from F and then our
node can inherit the value from its parent.
Bingo! ... an inherited attribute.
This can be accomplished by having the following two rules at the
node T.
T.tmp = F.val
T'.lval = T.tmp
Since we have no other use for T.tmp, we combine the above two rules into the first rule in the table.
Now lets look at the second multiplication (3*5)*4, where the parent of T' is another T'. (This is the normal case. When there are n multiplies, n-1 have T' as parent and only one has T).
The red-highlighted T' is the site for the multiplication. However, it needs as left operand, the product 3*5 that its parent can calculate. So we have the parent (another T' node, the blue one in this case) calculate the product and store it as an attribute of its right child namely the red T'. That is the first rule for T' in the table.
We have now explained the first, third, and last semantic rules. These are enough to calculate the answer. Indeed, if we trace it through, 60 does get evaluated and stored in the bottom right T', the one associated with the ε-production. Our remaining goal is to get the value up to the root where it represents the evaluation of this term T and can be combined with other terms to get the value of a larger expression.
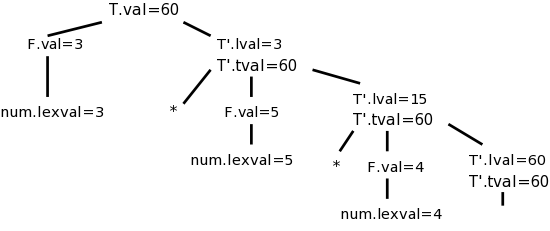
Going up is easy, just synthesize. I named the attribute tval, for term-value. It is generated at the ε-production from the lval attribute (which at this node is not a good name) and propagated back up. At the T node it is called simply val. At the right we see the annotated parse tree for this input.
Homework: Extend this SDD to handle the left-recursive, more complete expression evaluator given earlier in this section. Don't forget to eliminate the left recursion first.
It clearly requires some care to write the annotations.
Another question is how does the system figure out the evaluation order if one exists? That is the subject of the next section.
Remark: Consider the identifier table. The lexer creates it initially, but as the compiler performs semantic analysis and discover more information about various identifiers, e.g., type and visibility information, the table is updated. One could think of this is some inherited/synthesized attribute pair that during each phase of analysis is pushed down and back up the tree. However, it is not implemented this way; the table is made a global data structure that is simply updated. The the compiler writer must ensure manually that the updates are performed in an order respecting any dependences.
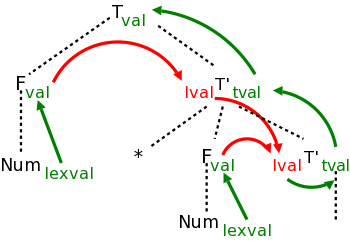
The diagram on the right illustrates a great deal. The black shows the parse tree for the multiplication grammar just studied when applied to a single multiplication, e.g. 3*5. The synthesized attributes are shown in green and are written to the right of the grammar symbol at the node where they are defined. The inherited attributes are shown in red and are written to the left of the grammar symbol where it is defined.
Each green arrow points to the attribute calculated from the attribute at the tail of the arrow. These arrows either go up the tree one level or stay at a node. That is because a synthesized attribute can depend only on the node where it is defined and that node's children. The computation of the attribute is associated with the production at the node at its arrowhead. In this example, each synthesized attribute depends on only one other, but that is not required.
Each red arrow also points to the attribute calculated from the attribute at the tail. Note that two red arrows point to the same attribute. This indicates that the common attribute at the arrowheads, depends on both attributes at the tails. According to the rules for inherited attributes, these arrows either go down the tree one level, go from a node to a sibling, or stay within a node. The computation of the attribute is associated with the production at the parent of the node at the arrowhead.
The graph just drawn is called the dependency graph. In addition to being generally useful in recording the relations between attributes, it shows the evaluation order(s) that can be used. Since the attribute at the head of an arrow depends on the on the one at the tail, we must evaluate the head attribute after evaluating the tail attribute.
Thus what we need is to find an evaluation order respecting the arrows. This is called a topological sort. The rule is that the needed ordering can be found if and only if there are no (directed) cycles. The algorithm is simple.
If the algorithm succeeds in deleting all the nodes, then the deletion order is a suitable evaluation order and there were no directed cycles.
Homework: The topological sort algorithm is nondeterministic (Choose a node) and hence there can be many topological sort orders. Find all the orders for the diagram above (you should label the nodes so you can describe the orders).
Given an SDD and a parse tree, it is easy to tell (by doing a topological sort) whether a suitable evaluation exists (and to find one).
However, a very difficult problem is, given an SDD, are there any parse trees with cycles in their dependency graphs, i.e., are there suitable evaluation orders for all parse trees. Fortunately, there are classes of SDDs for which a suitable evaluation order is guaranteed.
As mentioned above an SDD is S-attributed if every attribute is synthesized. For these SDDs all attributes are calculated from attribute values at the children since the other possibility, the tail attribute is at the same node, is impossible since the tail attribute must be inherited for such arrows. Thus no cycles are possible and the attributes can be evaluated by a postorder traversal of the parse tree.
Since postorder corresponds to the actions of an LR parser when reducing the body of a production to its head, it is often convenient to evaluate synthesized attributes during an LR parse.
Unfortunately, it is hard to live without inherited attributes.
So we define a class that permits certain kinds of inherited
attributes.
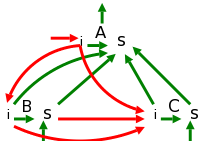
Definition: An SDD is L-Attributed if each attribute is either
from the left, and hence the name L-attributed.
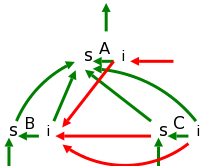
Case three must be handled specially whenever it occurs. The top picture to the right illustrates what the first two cases look like and suggest why there cannot be any cycles. The picture below it corresponds to a fictitious R-attributed definition. One reason L-attributed definitions are favored over R, is the left to right ordering in English. See the example below on type declarations and also consider the grammars that result from left recursion.
The picture shows
that there is an evaluation order for
L-attributed definitions (again assuming no case 3).
More formally, do a depth first traversal of the tree.
The first time you visit a node, evaluate its inherited attributes
(since you will know the value of everything it depends on), and the
last time you visit it, evaluate the synthesized attributes.
This is two-thirds
of an Euler-tour traversal.
Homework: Suppose we have a production A → B C D. Each of the four nonterminals has two attributes s, which is synthesized, and i, which is inherited. For each set of rules below, tell whether the rules are consistent with (i) an S-attributed definition, (ii) an L-attributed definition, (iii) any evaluation order at all.
| Production | Semantic Rule | Type |
|---|---|---|
| D → T L | L.type = T.type | inherited |
| T → INT | T.type = integer | synthesized |
| L → L1 , ID | L1.type = L.type | inherited |
| addType(ID.entry,L.type) | synthesized, side effect | |
| L → ID | addType(ID.entry,L.type) | synthesized, side effect |
When we have side effects such as printing or adding an entry to a table we must ensure that we have not added a constraint to the evaluation order that causes a cycle.
For example, the left-recursive SDD shown in the table on the right propagates type information from a declaration to entries in an identifier table.
The function addType adds the type information in the second argument to the identifier table entry specified in the first argument. Note that the side effect, adding the type info to the table, does not affect the evaluation order.
Draw the dependency graph on the board.
Note that the terminal ID has an attribute
(given by the
lexer) entry that gives its entry in the identifier table.
The nonterminal L has (in addition to L.type) a dummy synthesized
attribute, say AddType, that is a place holder for the addType()
routine.
AddType depends on the arguments of addType().
Since the first argument is from a child, and the second is an
inherited attribute of this node, we have legal dependences
for a synthesized attribute.
Note that we have an L-attributed definition.
Homework: For the SDD above, give the annotated parse tree for
INT a,b,c
Remark: See the new section Evaluating
L-Attributed Definitions
in section 5.2.4.
| Production | Semantic Rules |
|---|---|
| E → E 1 + T | E.node = new Node('+',E1.node,T.node) |
| E → E 1 - T | E.node = new Node('-',E1.node,T.node) |
| E → T | E.node = T.node |
| T → ( E ) | T.node = E.node |
| T → ID | T.node = new Leaf(ID,ID.entry) |
| T → NUM | T.node = new Leaf(NUM,NUM.val) |
Recall that in a syntax tree (technically an abstract syntax tree) we just have the essentials. For example 7+3*5, would have one + node, one *, and the three numbers. Lets see how to construct the syntax tree from an SDD.
Assume we have two functions Leaf(op,val) and Node(op,c1,...,cn), that create leaves and interior nodes respectively of the syntax tree. Leaf is called for terminals. Op is the label of the node (op for operation) and val is the lexical value of the token. Node is called for nonterminals and the ci's refer (are pointers) to the children.
| Production | Semantic Rules | Type |
|---|---|---|
| E → T E' | E.node=E'.syn | Synthesized |
| E'node=T.node | Inherited | |
| E' → + T E'1 | E'1.node=new Node('+',E'.node,T.node) | Inherited |
| E'.syn=E'1.syn | Synthesized | |
| E' → - T E'1 | E'1.node=new Node('-',E'.node,T.node) | Inherited |
| E'.syn=E'1.syn | Synthesized | |
| E' → ε | E'.syn=E'.node | Synthesized |
| T → ( E ) | T.node=E.node | Synthesized |
| T → ID | T.node=new Leaf(ID,ID.entry) | Synthesized |
| T → NUM | T.node=new Leaf(NUM,NUM.val) | Synthesized |
The upper table on the right shows a left-recursive grammar that is S-attributed (so all attributes are synthesized).
Try this for x-2+y and see that we get the syntax tree.
When we eliminate the left recursion, we get the lower table on the right. It is a good illustration of dependencies. Follow it through and see that you get the same syntax tree as for the left-recursive version.
Remarks:
This course emphasizes top-down parsing (at least for the labs) and
hence we must eliminate left recursion.
The resulting grammars need inherited attributes, since operations
and operands are in different productions.
But sometimes the language itself demands inherited attributes.
Consider two ways to describe a 3x4, two-dimensional array.
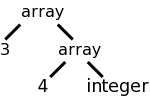
array [3] of array [4] of int and int[3][4]
Assume that we want to produce a structure like the one the right for the array declaration given above. This structure is generated by calling a function array(num,type). Our job is to create an SDD so that the function gets called with the correct arguments.
For the first language representation of arrays (found in Ada and
similar to that in lab 3), it is easy to generate an S-attributed
(non-left-recursive) grammar based on
A → ARRAY [ NUM ] OF A | INT | FLOAT
This is shown in the table on the left.
| Production | Semantic Rules | Type |
|---|---|---|
| T → B C | T.t=C.t | Synthesized |
| C.b=B.t | Inherited | |
| B → INT | B.t=integer | Synthesized |
| B → FLOAT | B.t=float | Synthesized |
| C → [ NUM ] C1 | C.t=array(NUM.val,C1.t) | Synthesized |
| C1.b=C.b | Inherited | |
| C → ε | C.t=C.b | Synthesized |
| Production | Semantic Rule |
|---|---|
| A → ARRAY [ NUM ] OF A1 | A.t=array(NUM.val,A1.t) |
| A → INT | A.t=integer |
| A → FLOAT | A.t=float |
On the board draw the parse tree and see that simple synthesized attributes above suffice.
For the second language representation of arrays (the C-style), we need some smarts (and some inherited attributes) to move the int all the way to the right. Fortunately, the result, shown in the table on the right, is L-attributed and therefore all is well.
Homework: 5.6
Basically skipped.
The idea is that instead of the SDD approach, which requires that we build a parse tree and then perform the semantic rules in an order determined by the dependency graph, we can attach semantic actions to the grammar (as in chapter 2) and perform these actions during parsing, thus saving the construction of the parse tree.
But except for very simple languages, the tree cannot be eliminated. Modern commercial quality compilers all make multiple passes over the tree, which is actually the syntax tree (technically, the abstract syntax tree) rather than the parse tree (the concrete syntax tree).
If parsing is done bottom up and the SDD is S-attributed, one can generate an SDT with the actions at the end (hence, postfix). In this case the action is perform at the same time as the RHS is reduced to the LHS.
Skipped.
Skipped
Skipped
Skipped
A good summary of the available techniques.
Recall that in recursive-descent parsing there is one procedure for each nonterminal. Assume the SDD is L-attributed. Pass the procedure the inherited attributes it might need (different productions with the same LHS need different attributes). The procedure keeps variables for attributes that will be needed (inherited for nonterminals in the body; synthesized for the head). Call the procedures for the nonterminals. Return all synthesized attributes for this nonterminal.
Requires an LL (not just LR) language.
Assume we have a parse tree as produced, for example, by your lab3. You now want to write the semantics analyzer, or intermediate code generator, and you have these semantic rules or actions that need to be performed. Assume the grammar is L-attributed, so we don't have to worry about dependence loops.
You start to write
As described in 5.5.1 above, you have received as parameters (in addition to tree-node), the attributes you are to inherit. You then call yourself recursively, with the tree-node argument set to your leftmost child, then call again using the next child, etc. Each time, you pass to the child the attributes it needs to inherit (You may be giving it too many since you know the nonterminal represented by this child but not the production; you could find out the production by examining the child's children, but probably don't bother doing so.)
When each child returns, it supplies as its return value the synthesized attributes it is passing back to you.
After the last child returns, you return to your caller, passing back the synthesized attributes you are to calculate.
Remark: This corresponds to chapters 6 and 8 in the first edition. The change is that storage management is now done after intermediate code generation.
Homework: Read Chapters 6 and 8.
Remark: This is 8.1 in 1e.
The difference between a syntax DAG and a syntax tree is that the
former can have undirected cycles.
DAGs are useful where there are multiple, identical portions in a
given input.
The common case of this is for expressions where there often are
common subexpressions.
For example in the expression
X + a + b + c - X + ( a + b + c )
each individual variable is a common subexpression.
But a+b+c is not since the first occurrence has the X already
added.
This is a real difference when one considers the possibility of
overflow or of loss of precision.
The easy case is
x + y * z * w - ( q + y * z * w )
where y*z*w is a common subexpression.
It is easy to find these. The constructor Node() above checks if an identical node exists before creating a new one. So Node ('/',left,right) first checks if there is a node with op='/' and children left and right. If so, a reference to that node is returned; if not, a new node is created as before.
Homework: Construct the DAG for
((x+y)-((x+y)*(x-y)))+((x+y)*(x-y))
Often one stores the tree or DAG in an array, one entry per node. Then references to the array index of a node is called the node's value-number. Searching an unordered array is slow; there are many better data structures to use. Hash tables are a good choice.
Instructions of the form op a,b,c, where op is
a primitive
operator.
For example
lshift a,b,4 // left shift b by 4 and place result in a
add a,b,c // a = b + c
a = b + c // alternate (more natural) representation of above
If we are starting with a DAG (or syntax tree if less aggressive), then transforming into 3-address code is just a topological sort and an assignment of a 3-address operation with a new name for the result to each interior node (the leaves already have names and values).
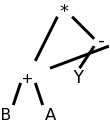
For example, (B+A)*(Y-(B+A)) produces the DAG on the right, which yields the following 3-address code.
t1 = B + A
t2 = Y - t1
t3 = t1 * t2
We use the term 3-address when we view the (intermediate-)
code as having one elementary
operation with three
operands, each of which is an address.
Typically two of the addresses represent source operands or
arguments of the operation and the third represents the result.
Some of the 3-address operations have fewer than three addresses; we
simply think of the missing addresses as unused (or ignored) fields
in the instruction.
There is no universally agreed to set of three-address instructions or to whether 3-address code should be the intermediate code for the compiler. Some prefer a set close to a machine architecture. Others prefer a higher-level set closer to the source, for example, subsets of C have been used. Others prefer to have multiple levels of intermediate code in the compiler with one phase of compilation being converting from the high-level intermediate code into the low-level intermediate code. What follows is the set proposed in the 2ed; it looks to be essentially the same as that in the 1e.
In the list below, x, y, and z are addresses, i is an integer, and
L is a symbolic label, as used in
chapter 2.
The instructions can be thought of as numbered and the labels can be
converted to the numbers with another pass over the output or
via backpatching
, which is discussed below.
Homework: 8.1
An easy way to represent the three address instructions: put the op into the first of four fields and the addresses into the remaining three. Some instructions do not use all the fields. Many operands will be references to entries in tables (e.g., the identifier table).
Optimization to save a field. The result field of a quad is omitted in a triple since the result is often a temporary.
When this result occurs as a source operand of a subsequent instruction, we indicate it by writing the value-number of the first instruction (distinguished some way, say with parens) as the operand of the second.
If the result field of a quad is not a temporary then two triples may be needed: One to do the operation and place the result into a temporary (which is not a field of the instruction). The second operation is a copy operation from the temporary to the final home. Recall that a copy does not use all the fields of a quad no fits into a triple without omitting the result.
When an optimizing compiler reorders instructions for increased performance, extra work is needed with triples since the instruction numbers, which have changed, are used implicitly. Hence the triples must be regenerated with correct numbers as operands.
Indirect triples. Keep an array of pointers to triples and, if it is necessary to reorder instructions, just reorder these pointers. This has two advantages.
This has become a big deal in modern optimizers, but we will
largely ignore it.
The idea is that you have all assignments go to unique (temporary)
variables.
So if the code is
if x then y=4 else y=5
it is treated as though it was
if x then y1=4 else y2=5
The interesting part comes when y is used later in the program and
the compiler must choose between y1 and y2.
Much of the early part of this section is really programming languages. In 1e this is section 6.1 (back from chapter 8).
A type expression is either a basic type or the result of applying a type constructor.
Definition: A type expression is one of the following.
There are two camps, name equivalence and structural equivalence.
Consider the following for example.
declare
type MyInteger is new Integer;
MyX : MyInteger;
x : Integer := 0;
begin
MyX := x;
end
This generates a type error in Ada, which has name equivalence since
the types of x and MyX do not have the same name, although they have
the same structure.
When you have an object of an anonymous
type as in
x : array [5] of integer;
it doesn't have the same type as any other object even
y : array [5] of integer;
But x[2] has the same type as y[3]; both are integers.
The following from 2ed uses C/Java array notation. The 1ed has pascal-like material (section 6.2). Although I prefer Ada-like constructs as in lab 3, I realize that the class knows C/Java best so like the authors I will go with the 2ed. I will try to give lab3-like grammars as well.
This grammar gives C/Java like records/structs/methodless-classes as well as multidimensional arrays (really arrays of arrays).
D → T id ; D | ε
T → B C | RECORD { D }
B → INT | FLOAT
C → [ NUM ] C | ε
The lab 3 grammar doesn't support records and the support for multidimensional arrays is flawed (you can define the type, but not a (constrained) object). Here is the part of the lab3 grammar that handles declarations of ints, reals and arrays.
declarations → declaration declarations | ε
declaration → object-declaration | type-declaration
object-declaration → defining-identifier : object-definition ;
object-definition → type-name | type-name [ NUMBER ]
type-declaration → TYPE defining-identifier IS ARRAY OF type-name ;
defining-identifier → IDENTIFIER
type-name → IDENTIFIER | INT | REAL
So that the tables below are not too wide, let's use shorter names
ds → d ds | ε
d → od | td
od → di : odef ;
odef → tn | tn [ NUM ]
td → TYPE di IS ARRAY OF tn ;
di → ID
tn → ID | INT | REAL
Ada supports both constrained array types such as
type t1 is array [5] of integer
and unconstrained array types (as in lab 3) such as
type t2 is array of integer
With the latter, the constraint is specified when the array (object)
itself is declared.
x1 : t1
x2 : t2[5]
The grammar in lab3 supports t2 and x2, but not t1 and x1.
The deficiency of the lab3 grammar is that for two dimensional array
types
type t3 is array of t2
we have no way to supply the two array bounds in the array (object)
definition.
Ada, which as said above, has both constrained and unconstrained
array types, forbids the latter from appearing after
is array of
.
You might wonder why we want the unconstrained type. These types permit a procedure to have a parameter that is an array of integers of unspecified size. Remember that the declaration of a procedure specifies only the type of the parameter; the object is determined at the time of the procedure call.
See section 8.2 in 1e (we are going back to chapter 8 from 6, so perhaps Doc Brown from BTTF should give the lecture).
We are considering here only those types for which the storage can be computed at compile time. For others, e.g., string variables, dynamic arrays, etc, we would only be reserving space for a pointer to the structure; the structure itself is created at run time and is discussed in the next chapter.
The idea is that the basic type determines the width of the data,
and the size of an array determines the height
.
These are then multiplied to get the size (area) of the data.
The book uses semantic actions (i.e., a syntax directed translation SDT). I added the corresponding semantic rules so that we have an SDD as well.
Remember that for an SDT, the placement of the actions withing the production is important. Since it aids reading to have the actions lined up in a column, we sometimes write the production itself on multiple lines. For example the production T→BC has the B and C on separate lines so that the action can be in between even though it is written to the right of both.
The actions use global variables t and w to carry the base type (INT or FLOAT) and width down to the ε-production, where they are then sent on their way up and become multiplied by the various dimensions. In the rules I use inherited attributes bt and bw. This is similar to the comment above that instead of having the identifier table passed up and down via attributes, the bullet is bitten and a globally visible table is used.
The base types and widths are set by the lexer or are constants in the parser.
| Production | Actions | Semantic Rules | Kind |
|---|---|---|---|
| T → B | { t = B.type; w = B.width; } | C.bt = B.bt | Inherited |
| C | { T.type = C.type; T.width = B.width; } | ||
| B → INT | { B.type = integer; B.width = 4; } | B.bt = integer B.bw = 4 | Synthesized Synthesized |
| B → FLOAT | { B.type = float; B.width = 8; } | B.bt = integer B.bw = 8 | Synthesized Synthesized |
| C → [ NUM ] C1 | C.type = array(NUM.value, C1.type) | Synthesized | |
| C.width = NUM.value * C1.width; | Synthesized | ||
| { C.type = array(NUM.value, C1.type); | C1.bt = C.bt | Inherited | |
| C.width = NUM.value * C1.width; } | C1.bw = C.bw | Inherited | |
| C → ε | C.type = t; C.width=w | C.type = C.bt C.width = C.bw | Synthesized Synthesized |
| Production | Semantic Rules |
|---|---|
| d → od | d.width = od.width |
| d → td | d.width = 0 |
| od → di : odef ; | addType(di.entry, odef.type) |
| od.width = odef.width | |
| di → ID | di.entry = ID.entry |
| odef → tn | odef.type = tn.type |
| odef.width = tn.width | |
| tn.type must be integer or real | |
| tn → INT | tn.type = integer |
| tn.width = 4 | |
| tn → REAL | tn.type = real |
| tn.width = 8 |
First let's ignore arrays. Then we get the simple table on the right. All the attributes are Synthesized so we have an S-attributed grammar.
We dutifully synthesize the width attribute all the way to the top and then do not use it. We shall use it in the next section when we consider multiple declarations.
Recall that addType is viewed as a synthesized since its parameters
come from the RHS, i.e., from children of this node.
It has a side effect (of modifying the identifier table) so we must
be sure that we are not depending on some order of evaluation that
is not simply parent after children
.
In fact, later when we evaluate expressions, we will need some of this information.
We will need to enforce declaration before use
since we will be looking
up information that we are setting here.
So in evaluation, we check the entry in the identifier table to be sure that the
type (for example) has already been set.
Note the comment tn.type must be integer or real
.
This is an example of a type check, a key component of semantic
analysis, that we will learn about soon.
The reason for it here is that we are only able to handle 1
dimensional arrays with the lab3 grammar.
(It would be a more complicated grammar with other type check rules
to handle the general case found in ada).
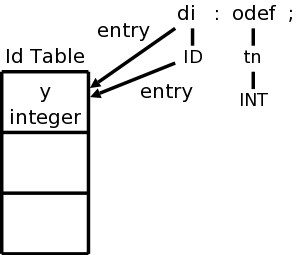
On the board, construct the parse tree, starting from the declaration
for
y: int ;
We should get the diagram on the right.
Now let's consider arrays. We need to include td (type-definition) and tn (type-name) as well as an additional production for od (object-definition). For td we need the restriction that tn is a basic type since we cannot define higher dimensional arrays.
I put in many type checks to distinguish the array case from the scalar case; possibly some are superfluous.
Once again all attributes are synthesized (including those with side effects) so we have an S-attributed SDD.
| Production | Semantic Rules |
|---|---|
| d → od | d.width = od.width |
| d → td | d.width = 0 |
| od → di : odef ; | addType(di.entry, odef.type)
od.width = odef.width |
| di → ID | di.entry = ID.entry |
| odef → tn | odef.type = tn.type |
| odef.width = tn.width | |
| tn.type must be integer or real | |
| odef → tn [ NUM ] | odef.type = array(NUM.value, getBaseType(tn.entry.type) |
| odef.width = sizeof(odef.type)
= NUM.value*sizeof(getBaseType(tn.entry.type)) | |
| tn must be ID | |
| td → TYPE di IS ARRAY OF tn ; | addType(di.entry, Array(*, tn.type)) |
| tn.type must be integer or real | |
| tn → ID | tn.entry = ID.entry |
| ID.entry.type must be array() | |
| tn → INT | tn.type = integer |
| tn.width = 4 | |
| tn → REAL | tn.type = real |
| tn.width = 8 |
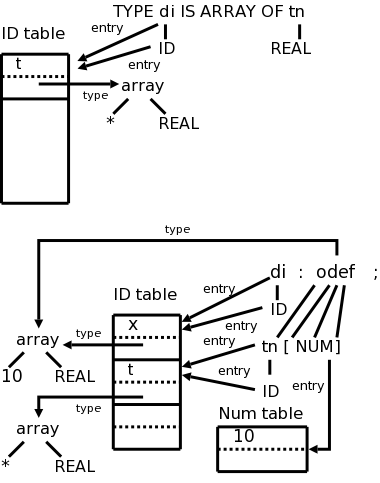
The top diagram on the right shows the result of applying the
semantic actions in the table above to to the declaration
type t is array of real;
The middle diagram shows the result after
x : t[10];
The diagram below parses the following program using the lab grammar. Actually the diagram cheats since the lab grammar requires a statement and the diagram pretends that statement can be ε.
Procedure P1 is
y : integer;
type t is array of real ;
x : t[10];
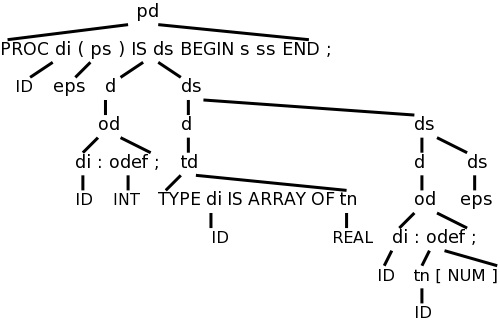
Be careful to distinguish three methods used to store and pass information.
To summarize, the identifier table (and others we have used) are not present when the program is run. But there must be run time storage for objects. We need to know the address each object will have during execution. Specifically, we need to know its offset from the start of the area used for object storage.
For just one object, it is trivial: the offset is zero.
The goal is to permit multiple declarations in the same procedure (or program or function). For C/java like languages this can occur in two ways.
In either case we need to associate with the object being declared its storage location. Specifically we include in the table entry for the object, its offset from the beginning of the current procedure. We initialize this offset at the beginning of the procedure and increment it after each object declaration.
The programming languages Ada and Pascal do not permit multiple
objects in a single declaration.
Both languages are of the
object : type
school.
Thus lab 3, which follows Ada, and 1e, which follows pascal, do not
support multiple objects in a single declaration.
C/Java certainly does permit multiple objects, but surprisingly
the 2e grammar does not.
Naturally, the way to permit multiple declarations is to have a
list of declarations in the natural right-recursive way.
The 2e C/Java grammar has D which is a list of semicolon-separated
T ID's
D → T ID ; D | ε
The lab 3 grammar has a list of declarations
(each of which ends in a semicolon).
Shortening declarations to ds we have
ds → d ds | ε
As mentioned, we need to maintain an offset, the next storage location to be used by an object declaration. The 2e snippet below introduces a nonterminal P for program that gives a convenient place to initialize offset.
P → { offset = 0; }
D
D → T ID ; { top.put(id.lexeme, T.type, offset);
offset = offset + T.width; }
D1
D → ε
The name top is used to signify that we work with the top symbol table (when we have nested scopes for record definitions we need a stack of symbol tables). Top.put places the identifier into this table with its type and storage location. We then bump offset for the next variable or next declaration.
Rather that figure out how to put this snippet together with the previous 2e code that handled arrays, we will just present the snippets and put everything together on the lab 3 grammar.
In the function-def (fd) and procedure-def (pd) productions we add the inherited attribute offset to declarations (ds.offset) and set it to zero. We then inherit this offset down to an individual declaration. If this is an object declaration, we store it in the entry for the identifier being declared and we increment the offset by the size of this object. When we get the to the end of the declarations (the ε-production), the offset value is the total size needed. So we turn it around and send it back up the tree.
| Production | Semantic Rules | Kind |
|---|---|---|
| fd → FUNC di ( ps ) RET tn IS ds BEG s ss END ; | ds.offset = 0 | Inherited |
| pd → PROC di ( ps ) IS ds BEG s ss END ; | ds.offset = 0 | Inherited |
| s.next = newlabel() | Inherited | |
| ss.next = newlabel() | Inherited | |
| pd.code = s.code || label(s.next) || ss.code || label(ss.next) | Synthesized | |
| ds → d ds1 | d.offset = ds.offset | Inherited |
| ds1.offset = d.newoffset | Inherited | |
| ds.totalSize = ds1.totalSize | Synthesized | |
| ds → ε | ds.totalSize = ds.offset | Synthesized |
| d → od | od.offset = d.offset | Inherited |
| d.newoffset = d.offset + od.width | Synthesized | |
| d → td | d.newoffset = d.offset | Synthesized |
| od → di : odef ; | addType(di.entry, odef.type) | Synthesized |
| od.width = odef.width | Synthesized | |
| addOffset(di.entry, od.offset) | Synthesized | |
| di → ID | di.entry = ID.entry | Synthesized |
| odef → tn | odef.type = tn.type | Synthesized |
| odef.width = tn.width | Synthesized | |
| tn.type must be integer or real | ||
| odef → tn [ NUM ] | odef.type = array(NUM.value, getBaseType(tn.entry.type)) | Synthesized |
| odef.width = sizeof(odef.type) | Synthesized | |
| tn must be ID | ||
| td → TYPE di is ARRAY OF tn ; | addType(di.entry, array(*, tn.type)) | Synthesized |
| tn.type must be integer or real | ||
| tn → ID | tn.entry = ID.entry | Synthesized |
| ID.entry.type must be array() | ||
| tn → INT | tn.type = integer | Synthesized |
| tn.width = 4 | Synthesized | |
| tn → REAL | tn.type = real | Synthesized |
| tn.width = 8 | Synthesized |
Now show what happens when the following program is parsed and the semantic rules above are applied.
procedure test () is
y : integer;
type t is array of real;
x : t[10];
begin
y = 5; // we haven't yet done statements
x[2] = y; // type error?
end;
Since records can essentially have a bunch of declarations inside,
we only need add
T → RECORD { D }
to get the syntax right.
For the semantics we need to push the environment and offset onto
stacks since the namespace inside a record is distinct from that on
the outside.
The width of the record itself is the final value of (the inner)
offset.
T → record { { Env.push(top); top = new Env()
Stack.puch(offset); offset = 0; }
D } { T.type = record(top); T.width = offset;
top = Env.pop(); offset = Stack.pop(); }
This does not apply directly to the lab 3 grammar since the grammar does not have records. It does, however, have procedures that can be nested. If we wanted to generate code for nested procedures we would need to stack the symbol table as done here in 2e.
Homework: Determine the types and relative addresses for the identifiers in the following sequence of declarations.
float x;
record { float x; float y; } rec;
float y;
Remark: See 8.3 in 1e.
| Production | Semantic Rule |
|---|---|
| as → lv = e | as.code = e.code || gen(lv.lexeme = e.addr) |
| lv → ID | lv.lexeme = get(ID.lexeme) |
| e → t | e.addr = t.addr |
| e.code = t.code | |
| e → e1 + t | e.addr = new Temp() |
| e.code = e1.code || t.code || gen(e.addr = e1.addr + t.addr) | |
| e → e1 - t | e.addr = new Temp() |
| e.code = e1.code || t.code || gen(e.addr = e1.addr - t.addr) | |
| t → f | t.addr = f.addr |
| t.code = f.code | |
| t → t1 * f | t.addr = new Temp() |
| t.code = t1.code || f.code || gen(t.addr = t1.addr * f.addr) | |
| t → t1 / f | t.addr = new Temp() |
| t.code = t1.code || f.code || gen(t.addr = t1.addr / f.addr) | |
| f → ( e ) | f.addr = e.addr |
| f.code = e.code | |
| f → ID | f.addr = get(ID.lexeme) |
| f.code = "" | |
| f → NUM | f.addr = get(NUM.lexeme) |
| f.code = "" |
The goal is to generate 3-address code for expressions.
We will generate them using the natural
notation of
6.2.
In fact we assume there is a function gen() that given the pieces
needed does the proper formatting so gen(x = y + z) will output the
corresponding 3-address code.
gen() is often called with addresses rather than lexemes like x.
The constructor Temp() produces a new address in whatever format gen
needs.
Hopefully this will be clear in the tables that follow
In fact, we do a little more and generate code for assignment statements.
We will use two attributes code and address. For a parse tree node the code attribute gives the three address code to evaluate the input derived from that node. In particular, code at the root performs the entire assignment statement. there.
The attribute addr at a node is the address that holds the value calculated by the code at the node. Recall that unlike real code for a real machine our 3-address code doesn't reuse addresses.
As one would expect for expressions, all the attributes in the
table to the right are synthesized.
The table is for the expression part of the lab 3 grammar.
To save space let's use as for assignment-statement, lv for lvalue,
e for expression, t for term, and f for factor.
Since we will be covering arrays a little later, we do not consider
LET array-element
.
We saw this in chapter 2.
The method in the previous section generates long strings and we walk the tree. By using SDT instead of using SDD, you can output parts of the string as each node is processed.
The idea is that you associate the base address with the array name. That is, the offset stored in the identifier table is the address of the first element of the array. The indices and the array bounds are used to compute the amount, often called the offset (unfortunately, we have already used that term), by which the address of the referenced element differs from the base address.
For one dimensional arrays, this is especially easy: The address increment is the width of each element times the index (assuming indexes start at 0). So the address of A[i] is the base address of A plus i times the width of each element of A.
The width of each element is the width of what we have called the base type.
So for an ID the element width is sizeof(getBaseType(ID.entry.type)).
For convenience we define getBaseWidth by the formula
getBaseWidth(ID.entry) = sizeof(getBaseType(ID.entry.type))
Let us assume row major ordering. That is, the first element stored is A[0,0], then A[0,1], ... A[0,k-1], then A[1,0], ... . Modern languages use row major ordering.
With the alternative column major ordering, after A[0,0] comes A[1,0], A[2,0], ... .
For two dimensional arrays the address of A[i,j] is the sum of three terms
(In some languages A[i,j] is written A[i][j].)
The generalization to higher dimensional arrays is clear.
| Production | Semantic Rules |
|---|---|
| as → lv = e ; | as.code = e.code || lv.code || gen(*lv.addr = e.addr) |
| lv → ID | lv.addr = new Temp()
lv.code = gen(lv.addr = &get(ID.lexeme)) |
| lv → let ae | lv.addr = ae.addr
lv.code = ae.code |
| ae → ID [ e ] | ae.t1 = new Temp()
ae.t2 = new Temp() ae.addr = new Temp() ae.code = e.code || gen(ae.t1 = e.addr * getBaseWidth(ID.entry)) || gen(ae.t2 = &get(ID.lexeme)) || gen(ae.addr = ae.t2 + ae.t1) |
Let's go over this carefully, especially the generated code and its use of addresses.
The book (both additions are the same in this respect) included
a[i] as a legal address for three-address code.
Last time, I did not appreciate the significance of this
address form and thought it was just a convenience.
In fact it is a special form
.
special formsthat are evaluated differently.
special formin that we don't use the address of i but instead the value of i is added to the address of a.
It was definitely instructive for me! The rules for addresses in 3-address code also include
a = &b
a = *b
*a = b
which are other special forms. They have the same meaning as in C.
I believe the SDD on the right if given a[3]=5, with a an integer array will generate
t$1 = 3*4 // t$n are the temporary names from new TEMP()
t$2 = &a
t$3 = t$2 + t$1
*t3 = 5
I also added an & to the non-array production lv→ID so that both could be handled by the same semantic rule for as→lv=e.
Homework: Write the SDD using the a[i] special form instead of the & and * special forms.
This is an exciting moment. At long last we can compile a full program!
Recall the program we could partially handle.
procedure test () is
y : integer;
type t is array of real;
x : t[10];
begin
y = 5; // we haven't yet done statements
x[2] = y; // type error?
end;
Now we can do the statements.
What about the possible type error?
Let's take the last option.
Homework: What code is generated for the program written above?
Remark: We are back to chapter 6 in 1e.
Type Checking includes several aspects.
All type checking could be done at run time: The compiler generates code to do the checks. Some languages have very weak typing; for example, variables can change their type during execution. Often these languages need run-time checks. Examples include lisp, snobol, apl.
A sound type system guarantees that all checks can be performed prior to execution. This does not mean that a given compiler will make all the necessary checks.
An implementation is strongly typed if compiled programs are guaranteed to run without type errors.
There are two forms of type checking.
We consider type checking for expessions. Checking statements is very similar. View the statement as a function having its components as arguments and returning void.
A very strict type system would do no automatic conversion. Instead it would offer functions for the programer to explicitly convert between selected types. Then either the program has compatible types or is in error.
However, we will consider a more liberal approach in which the language
permits certain implicit conversions that the compiler is to supply.
This is called type coercion.
Explicit conversions supplied by the programmer are
called casts.
We continue to work primarily with the two types used in lab 3, namely integer and real, and postulate a unary function denoted (real) that converts an integer into the real having the same value. Nonetheless, we do consider the more general case where there are multiple types some of which have coercions (often called widening). For example in C/Java, int can be widened to long, which in turn can be widened to float as shown in the figure to the right.
Mathematically the hierarchy on the right is a partially order set (poset) in which each pair of elements has a least upper bound (LUB). For many binary operators (all the arithmetic ones we are considering, but not exponentiation) the two operands are converted to the LUB. So adding a short to a char, requires both to be converted to an int. Adding a byte to a float, requires the byte to be converted to a float (the float remains a float and is not converted).
The steps for addition, subtraction, multiplication, and division are all essentially the same: Convert each types if necessary to the LUB and then perform the arithmetic on the (converted or original) values. Note that conversion requires the generation of code.
Two functions are convenient.
LUB is simple, just look at the address latice. If one of the type arguments is not in the lattice, signal an error; otherwise find the lowest common ancestor.
widen is more interesting. It involves n2 cases for n types. Many of these are error cases (e.g., if t wider than w). Below is the code for our situation with two possible types integer and real. The four cases consist of 2 nops (when t=w), one error (t=real; w=integer) and one conversion (t=integer; w=real).
widen (a:addr, t:type, w:type, newcode:string, newaddr:addr)
if t=w
newcode = ""
newaddr = a
else if t=integer and w=real
newaddr = new Temp()
newcode = gen(newaddr = (real) a)
else signal error
With these two functions it is not hard to modify the rules to catch type errors and perform coercions for arithmetic expressions.
This requires that we have type information for the base entities, identifiers and numbers. The lexer can supply the type of the numbers. We retrieve it via get(NUM.type).
It is more interesting for the identifiers. We insert that information when we process declarations. So we now have another semantic check: Is the identifier declared before it is used?
I will use the function get(ID.type), which returns the type from the identifier table and signals an error if it is not there. The original SDD for assignment statements was here and the changes for arrays was here.
| Production | Semantic Rule |
|---|---|
| as → lv = e | widen(e.addr, e.type, lv.type, as.code1, as.addr1)
as.code = lv.code || e.code || as.code1 || gen(*lv.addr = as.addr1) |
| lv → ID | lv.addr = new TEMP() |
| lv.type = get(ID.type) | |
| lv.code = gen(lv.addr = &get(ID.lexeme)) | |
| lv → let ae | lv.addr = ae.addr |
| lv.type = ae.type | |
| lv.code = ae.code | |
| ae → ID [ e ] | ae.type = getBaseType(ID.entry.type)
ae.t1 = new Temp() ae.t2 = new Temp() ae.addr = new Temp() ae.code = e.code || gen(ae.t1 = e.addr * getBaseWidth(ID.entry)) || gen(ae.t2 = &get(ID.lexeme)) || gen(ae.addr = ae.t2 + ae.t1) |
| e → t | e.addr = t.addr |
| e.type = t.type | |
| e.code = t.code | |
| e → e1 + t | e.addr = new Temp() |
| e.type = LUB(e1.type, t.type) | |
| widen(e1.addr, e1.type, e.type, e.code1, e.addr1)
widen(t.addr, t.type, e.type, e.code2, e.addr2) e.code = e1.code || t.code || e.code1 || e.code2 || gen(e.addr = e.addr1 + e.addr2) | |
| e → e1 - t | e.addr = new Temp() |
| e.type = LUB(e1.type, t.type) | |
| widen(e1.addr, e1.type, e.type, e.code1, e.addr1)
widen(t.addr, t.type, e.type, e.code2, e.addr2) e.code = e1.code || t.code || e.code1 || e.code2 || gen(e.addr = e.addr1 - e.addr2) | |
| t → f | t.addr = f.addr |
| t.type = f.type | |
| t.code = f.code | |
| t → t1 * f | t.addr = new Temp() |
| t.type = LUB(t1.type, f.type) | |
| widen(t1.addr, t1.type, t.type, t.code1, t.addr1)
widen(f.addr, f.type, t.type, t.code2, t.addr2) t.code = t1.code || f.code || t.code1 || t.code2 || gen(t.addr = t.addr1 * t.addr2) | |
| t → t1 / f | t.addr = new Temp() |
| t.type = LUB(t1.type, f.type) | |
| widen(t1.addr, t1.type, t.type, t.code1, t.addr1)
widen(f.addr, f.type, t.type, t.code2, t.addr2) t.code = t1.code || f.code || t.code1 || t.code2 || gen(t.addr = t.addr1 / t.addr2) | |
| f → ( e ) | f.addr = e.addr |
| f.type = e.type | |
| f.code = e.code | |
| f → ID | f.addr = get(ID.lexeme) |
| f.type = get(ID.type) | |
| f.code = "" | |
| f → NUM | f.addr = get(NUM.lexeme) |
| f.type = get(NUM.type) | |
| f.code = "" |
Homework: Same question as the previous homework (What code is generated for the program written above?). But the answer is different!
Skipped.
Overloading is when a function or operator has several definitions depending on the types of the operands and result.
Skipped.
Skipped.
Remark: Section 8.4 in 1e.
Control flow includes the study of Boolean expressions, which have two roles.
One question that comes up with Boolean expressions is whether both
operands need be evaluated.
If we need to evaluate A or B
and find that A is true,
must we evaluate B?
For example, consider evaluating
A=0 OR 3/A < 1.2
when A is zero.
This comes up some times in arithmetic as well. Consider A*F(x). If the compiler knows that for this run A is zero must it evaluate F(x)? Don't forget that functions can have side effects,
This is also called jumping code.
Here the Boolean operators AND, OR, and NOT do not appear in the
generated instruction stream.
Instead we just generate jumps to either the true branch or the
false branch
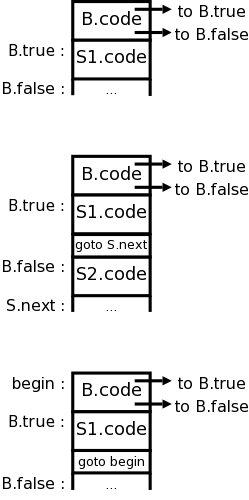
This time I will follow 2e and use C/Java grammar rather than lab 3 grammar since lab 3 is basically a subset.
So our grammar is (S for statement, B for boolean expression)
S → if ( B ) S1 S → if ( B ) S1 else S2 S → while ( B ) S1What is missing from lab 3 is the
elseless ifand Boolean operators.
The idea is simple.
| Production | Semantic Rules | Kind |
|---|---|---|
| P → S | S.next = newlabel() | Inherited |
| P.code = S.code || label(S.next) | Synthesized | |
| S → if ( B ) S1 | B.true = newlabel() | Inherited |
| B.false = S.next | Inherited | |
| S1.next = S.next | Inherited | |
| S.code = B.code || label(B.true) || S1.code | Synthesized | |
| S → if ( B ) S1 else S2 | B.true = newlabel() | Inherited |
| B.false = newlabel() | Inherited | |
| S1.next = S.next | Inherited | |
| S2.next = S.next | Inherited | |
| S.code = B.code || label(B.true) || S1.code
|| gen(goto S.next) || label(B.false) || S2.code | Synthesized | |
| S → while ( B ) S1 | begin = newlabel() | Synthesized |
| B.true = newlabel() | Inherited | |
| B.false = S.next | Inherited | |
| S1.next = begin | Inherited | |
| S.code = label(begin) || B.code || label(B.true) || S1.code || gen(goto begin) | Synthesized | |
| S → S1 S2 | S1.next = newlabel() | Inherited |
| S2.next = S.next | Inherited | |
| S.code = S1.code || label(S1.next) || S2.code | Synthesized | |
Homework: Give the SDD for a repeat statement
Repeat S while B
| Production | Semantic Rules | Kind |
|---|---|---|
| B → B1 || B2 | B1.true = B.true | Inherited |
| B1.false = newlabel() | Inherited | |
| B2.true = B.true | Inherited | |
| B2.false = B.false | Inherited | |
| B.code = B1.code || label(B1.false) || B2.code | Synthesized | |
| B → B1 && B2 | B1.true = newlabel() | inherited |
| B1.false = B.false | inherited | |
| B2.true = B.true | inherited | |
| B2.false = B.false | inherited | |
| B.code = B1.code || label(B1.true) || B2.code | Synthesized | |
| B → ! B1 | B1.true = B.false | Inherited |
| B1.false = B.true | Inherited | |
| B.code = B1.code | Synthesized | |
| B → E1 relop E2 | B.code = E1.code || E2.code
|| gen(if E1.addr relop.lexeme E2.addr goto B.true) || gen(goto B.false) | Synthesized |
| B → true | B.code = gen(goto B.true) | Synthesized |
| B → false | B.code = gen(goto B.false) | Synthesized |
| B → ID | B.code = gen(if get(ID.lexeme) goto B.true)
|| gen(goto B.false) | Synthesized |
Do on the board the translation of
if ( x < 5 || x > 10 && x == y ) x = 3 ;
We get
if x < 5 goto L2
goto L3
L3: if x > 10 goto L4
goto L1
L4: if x == y goto L2
goto L1
L2: x = 3
Note that there are three extra gotos. One is a goto the next statement. Two others could be eliminated by using ifFalse.
Skipped.
Remark: As mentioned before 6.6 in the notes is 6.6 in 2e and 8.4 in 1e. However the third level material is not is the same order. In particular this section (6.6.6) is very early in 8.4.
If ther are boolean variables (or variables into which a boolean value can be placed), we can have boolean assignment statements. That is we might evaluate boolean expressions outside of control flow statements.
Recall that the code we generated for boolean expressions (inside control flow statements) used inherited attributes to push down the tree the exit labels B.true and B.false. How are we to deal with Boolean assignment statements?
Up to now we have used the so called jumping code
method for
Boolean quantities.
We evaluated Boolean expressions (in the context of control flow
statements) by using inherited attributes to push down the tree the
true and false exits (i.e., the target locations to jump to if the
expression evaluates to true and false).
With this method if we have a Boolean assignment statement, we just let the true and false exits lead to statements
LHS = true
LHS = false
respectively.
In the second method we simply treat boolean expressions as
expressions.
That is, we just mimic the actions we did for integer/real
evaluations.
Thus Boolean assignment statements like
a = b OR (c AND d AND (x < y))
just work.
For control flow statements like
while (boolean-expression) statement-list end
if (boolean-expression) statement-list else statement-list end
we simply evaluate the boolean expression as if it was part of an
assignment statement and then have two jumps to where we should go
if the result is true or false.
However this is wrong. In C if (a=0 || 1/a > f(a)) is guaranteed not to divide by zero and the above implementation fails to provide this guarantee. We must somehow implement short-circuit boolean evaluation.
Skipped.
Our intermediate code uses symbolic labels.
At some point these must be translated into addresses of
instructions.
If we use quads all instructions are the same length so the address
is just the number of the instruction.
Sometimes we generate the jump before we generate the target so we
can't put in the instruction number on the fly
.
Indeed, that is why we used symbolic labels.
The easiest method of fixing this up is to make an extra pass (or
two) over the quads to determine the correct instruction number and
use that to replace the symbolic label.
This is extra work; a more efficient technique, which is independent
of compilation, is called backpatching
.
Evaluate an expression, compare it with a vector of constants that are viewed as labels of the arms of the switch, and execute the matching arm (or a default).
The C language is unusual in that the various cases are just labels
for a giant computed goto
at the beginning.
The more traditional idea is that you execute just one of the arms,
as in a series of
if
else if
else if
...
end if
else if'sabove. This executes roughly 2k jumps (worst case) for k cases.
The lab 3 grammar does not have a switch statement so we won't do a detailed SDD.
Such an SDD would be organized as follows.
Much of the work for procedures involves storage issues and the run time environment; this is discussed in the next chapter.
In order to support inter-procedural type checking by the compiler, we need to define the called procedure in the calling procedure, which the lab 3 grammar doesn't support except for calling itself recursively. So the best we can do is type check recursive calls.
The basic scheme for type checking recursive (or other calls) is to
generate a table entry for the procedure that contains
its signature
, i.e., the types of its parameters and its
result type.
Recall the SDD
for declarations.
These semantic rules pass up the totalSize to the
ds → d ds
production.
What is needed is for the ps (parameters) to do an analogous thing with their declarations but also (or perhaps instead) pass up a representation of the declarations themselves which when it reaches the top is the signature for a procedure and when put together with the return is the signature for a function.
More serious is supporting nested procedure definitions (defining a procedure inside a procedure). Lab 3 doesn't support this because a procedure or function definition is not a declaration. It would be easy to enhance the grammar to fix this, but the serious work is that then you need nested identifier tables.
Our lexer doesn't support this. So you would remove table building from the lexer and instead do it in the parser and when a new scope (procedure definition, record definition, begin block) arises you push the current tables on a stack and begin a new one. When the nested scope ends, you pop the tables.
Homework: Read Chapter 7.
We are discussing storage organization from the point of view of the compiler, which must allocate space for programs to be run. In particular, we are concerned with only virtual addresses and treat them uniformly.
This should be compared with an operating systems treatment, where we worry about how to effectively map this configuration to real memory. For example see see these two diagrams in my OS class notes, which illustrate an OS difficulty with our allocation method, which uses a very large virtual address range and one solution.
Some system require various alignment constraints. For example 4-byte integers might need to begin at a byte address that is a multiple of four. Unaligned data might be illegal or might lower performance. To achieve proper alignment padding is often used.
expansion region.
new, or via a library function call, such as malloc(). It is deallocated either by another executable statement, such as a call to free(), or automatically by the system.
Much (often most) data cannot be statically allocated. Either its size is not know at compile time or its lifetime is only a subset of the program's execution.
Early versions of Fortran used only statically allocated data. This required that each array had a constant size specified in the program. Another consequence of supporting only static allocation was that recursion was forbidden (otherwise the compiler could not tell how many versions of a variable would be needed).
Modern languages, including newer versions of Fortran, support both static and dynamic allocation of memory.
The advantage supporting dynamic storage allocation is the increased flexibility and storage efficiency possible (instead of declaring an array to have a size adequate for the largest data set; just allocate what is needed). The advantage of static storage allocation is that it avoids the runtime costs for allocation/deallocation and may permit faster code sequences for referencing the data.
An (unfortunately, all too common) error is a so-called memory leak
where a long running program repeated allocates memory that it fails
to delete, even after it can no longer be referenced.
To avoid memory leaks and ease programming, several programming
language systems employ automatic garbage collection
.
That means the runtime system itself can determine if data
can no longer be referenced and if so automatically deallocates it.
Achievements.
Recall the fibonacci sequence 1,1,2,3,5,8, ... defined by f(1)=f(2)=1 and, for n>2, f(n)=f(n-1)+f(n-2). Consider the function calls that result from a main program calling f(5). On the left we show the calls and returns linearly and on the right in tree form. The latter is sometimes called the activation tree or call tree.
System starts main
enter f(5)
enter f(4)
enter f(3)
enter f(2)
exit f(2)
enter f(1)
exit f(1)
exit f(3)
enter f(2) int a[10];
exit f(2) int main(){
exit f(4) int i;
enter f(3) for (i=0; i<10; i++){
enter f(2) a[i] = f(i);
exit f(2) }
enter f(1) }
exit f(1) int f (int n) {
exit f(3) if (n<3) return 1;
exit f(5) return f(n-1)+f(n-2);
main ends }
We can make the following observation about these procedure calls.

The information needed for each invocation of a procedure is kept in a runtime data structure called an activation record (AR) or frame. The frames are kept in a stack called the control stack.
At any point in time the number of frames on the stack is the current depth of procedure calls. For example, in the fibonacci execution shown above when f(4) is active there are three activation records on the control stack.
ARs vary with the language and compiler implementation. Typical components are described and pictured below. In the diagrams the stack grows down the page.
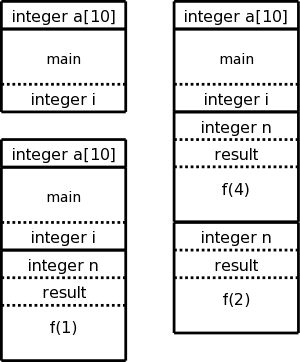
The diagram on the right shows (part of) the control stack for the fibonacci example at three points during the execution. In the upper left we have the initial state, We show the global variable a, although it is not in an activation record and actually is allocated before the program begins execution (it is statically allocated; recall that the stack and heap are each dynamically allocated). Also shown is the activation record for main, which contains storage for the local variable i.
Below the initial state we see the next state when main has called f(1) and there are two activation records, one for main and one for f. The activation record for f contains space for the parameter n and and also for the result. There are no local variables in f.
At the far right is a later state in the execution when f(4) has been called by main and has in turn called f(2). There are three activation records, one for main and two for f. It is these multiple activations for f that permits the recursive execution. There are two locations for n and two for the result.
The calling sequence, executed when one procedure (the caller) calls another (the callee), allocates an activation record (AR) on the stack and fills in the fields. Part of this work is done by the caller; the remainder by the callee. Although the work is shared, the AR is called the callee's AR.
Since the procedure being called is defined in one place, but called from many, there are more instances of the caller activation code than of the callee activation code. Thus it is wise, all else being equal, to assign as much of the work to the callee.
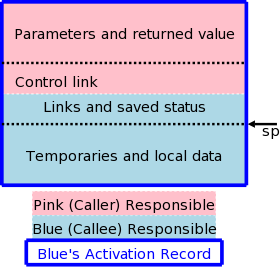
The top picture illustrates the situation where a pink procedure (the caller) calls a blue procedure (the callee). Also shown is Blue's AR. Note that responsibility for this single AR is shared by both procedures. The picture is just an approximation: For example, the returned value is actually the Blue's responsibility (although the space might well be allocated by Pink. Also some of the saved status, e.g., the old sp, is saved by Pink.
The bottom picture shows what happens when Blue, the callee, itself
calls a green procedure and thus Blue is also a caller.
You can see that Blue's responsibility includes part of its AR as
well as part of Green's.
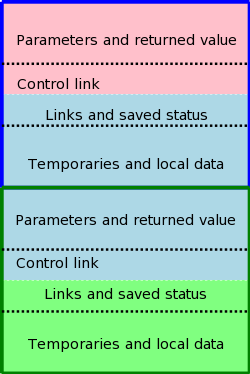
Note that varagrs are supported.
There are two flavors of variable-length data.
It is the second flavor that we wish to allocate on the stack. The goal is for the (called) procedure to be able to access these arrays using addresses determinable at compile time even though the size of the arrays (and hence the location of all but the first) is not know until the program is called and indeed often differs from one call to the next.
The solution is to leave room for pointers to the arrays in the AR. These are fixed size and can thus be accessed using static offsets. Then when the procedure is invoked and the sizes are known, the pointers are filled in and the space allocated.
A small change caused by storing these variable size items on the stack is that it no longer is obvious where the real top of the stack is located relative to sp. Consequently another pointer (call it real-top-of-stack) is also kept. This is used on a call to tell where the new allocation record should begin.
As we shall see the ability of procedure p to access data declared outside of p (either declared globally outside of all procedures or declared inside another procedure q) offers interesting challenges.
In languages like standard C without nested procedures, visible names are either local to the procedure in question or are declared globally.
With nested procedures a complication arises. Say g is nested inside f. So g can refer to names declared in f. These names refer to objects in the AR for f; the difficulty is finding that AR when g is executing. We can't tell at compile time where the (most recent) AR for f will be relative to the current AR for g since a dynamically-determined number of routines could have been called in the middle.
There is an example in the next section. in which g refers to x, which is declared in the immediately outer scope (main) but the AR is 2 away because f was invoked in between. (In that example you can tell at compile time what was called in what order, but with a more complicated program having data-dependent branches, it is not possible.)
As we have discussed, the 1e, which you have, uses pascal, which many of you don't know. The 2e, which you don't have uses C, which you do know.
Since pascal supports nested procedures, this is what the 1e uses to give examples.
The 2e asserts (correctly) that C doesn't have nested procedures so introduces ML, which does (and is quite slick), but which unfortunately many of you don't know and I haven't used. Fortunately a common extension to C is to permit nested procedures. In particular, gcc supports nested procedures. To check my memory I compiled and ran the following program.
#include <stdio.h>
int main (int argc, char *argv[])
{
int x = 10;
void g(int y)
{
int z = x;
return;
}
int f (int y)
{
g(y);
return y+1;
}
printf("The answer is %d\n", f(x));
return 0;
}
The program compiles without errors and the correct answer of 11 is printed.
So we can use C (really the GCC, et al extension of C).
Outermost procedures have nesting depth 1. Other procedures have nesting depth 1 more than the nesting depth of the immediately outer procedure. In the example above main has nesting depth 1; both f and g have nesting depth 2.
The AR for a nested procedure contains an access link that points to the AR of the (most recent activation of the immediately outer procedure). So in the example above the access link for all activations of f and g would point to the AR of the (only) activation of main. Then for a procedure P to access a name defined in the 3-outer scope, i.e., the unique outer scope whose nesting depth is 3 less than that of P, you follow the access links three times.
The question is how are the access links maintained.
Let's assume there are no procedure parameters. We are also assuming that the entire program is compiled at once. For multiple files the main issues involve the linker, which is not covered in this course. I do cover it a little in the OS course.
Without procedure parameters, the compiler knows the name of the called procedure and, since we are assuming the entire program is compiled at once, knows the nesting depth.
Let the caller be procedure R (the last letter in caller) and let the called procedure be D. Let N(f) be the nesting depth of f. I did not like the presentation in 2e (which had three cases and I think did not cover the example above). I made up my own and noticed it is much closer to 1e (but makes clear the direct recursion case, which is explained in 2e). I am surprised to see a regression from 1e to 2e, so make sure I have not missed something in the cases below.
P() {
D() {...}
P1() {
P2() {
...
Pk() {
R(){... D(); ...}
}
...
}
}
}
Our goal while creating the AR for D at the call from R is to set
the access link to point to the AR for P.
Note that this entire structure in the skeleton code shown is
visible to the compiler.
Thus, the current (at the time of the call) AR is the one for R
and if we follow the access links k+1 times we get a pointer to
the AR for P, which we can then place in the access link for the
being-created AR for D.
When k=0 we get the gcc code I showed before and also the case of direct recursion where D=R.
Basically skipped. The problem is that, if f calls g giving with a parameter of h (or a pointer to h in C-speak) and the g calls this parameter (i.e., calls h), g might not know the context of h. The solution is for f to pass to g the pair (h, the access link of h) instead of just passing h. Naturally, this is done by the compiler, the programmer is unaware of access links.
Basically skipped. In theory access links can form long chains (in practice nesting depth rarely exceeds a dozen or so). A display is an array in which entry i points to the most recent (highest on the stack) AR of depth i.
Almost all of this section is covered in the OS class.
Covered in OS.
Covered in Architecture.
Covered in OS.
Covered in OS.
Stack data is automatically deallocated when the defining procedure returns. What should we do with heap data explicated allocated with new/malloc?
The manual method is to require that the programmer explicitly deallocate these data. Two problems arise.
loop
allocate X
use X
forget to deallocate X
As this program continues to run it will require more and more
storage even though is actual usage is not increasing
significantly.
allocate X
use X
deallocate X
100,000 lines of code not using X
use X
Both can be disastrous.
The system detects data that cannot be accessed (no direct or indirect references exist) and deallocates the data automatically.
Covered in programming languages???
Skipped
Skipped
Skipped.
Remark: This is chapter 9 in 1e.
Homework: Read Chapter 8.
Goal: Transform intermediate code + tables into final machine (or assembly) code. Code generation + Optimization is the back end of the compoiler.
As expected the input is the output of the intermediate code generator. We assume that all syntactic and semantic error checks have been done by the front end. Also all needed type conversions are already done and any type errors have been detected.
We are using three address instructions for our intermediate language. The these instructions have several representations, quads, triples, indirect triples, etc. In this chapter I will tend to write quads (for brevity) when I should write three-address instructions.
A RISC (Reduced Instruction Set Computer), e.g. PowerPC, Sparc, MIPS (popular for embedded systems), is characterized by
Onlyloads and stores touch memory
A CISC (Complex Instruct Set Computer), e.g. x86, x86-64/amd64 is characterized by
A stack-based computer is characterized by
Noregisters
IBM 701/704/709/7090/7094 (Moon shot, MIT CTSS) were accumulator based.
Stack based machines were believed to be good compiler targets. They became very unpopular when it was believed that register architecture would perform better. Better compilation (code generation) techniques appeared that could take advantage of the multiple registers.
Pascal P-code and Java byte-code are the machine instructions for a hypothetical stack-based machine, the JVM (Java Virtual Machine) in the case of Java. This code can be interpreted, or compiled to native code.
RISC became all the rage in the 1980s.
CISC made a gigantic comeback in the 90s with the intel pentium
pro.
A key idea of the pentium pro is that the hardware would
dynamically translate a complex x86 instruction into a series of
simpler RISC-like
instructions called ROPs (RISC ops).
The actual execution engine dealt with ROPs.
The jargon would be that, while the architecture (the ISA) remained
the x86, the micro-architecture was quite different and more like
the micro-architecture seen in previous RISC processors.
For maximum compilation speed, the compiler accepts the entire
program at once and produces code that can be loaded and executed
(the compilation system can include a simple loader and can start
the compiled program).
This was popular for student jobs
when computer time was
expensive.
The alternative, where each procedure can be compiled separately,
requires a linkage editor.
It eases the compiler's task to produce assembly code instead of machine code and we will do so. This decision increased the total compilation time since it requires an extra assembler pass (or two).
A big question is the level of code quality we seek to attain.
For example can we simply translate one quadruple at a time.
The quad
x = y + z
can always (assuming x, y, and z are statically allocated, i.e.,
their address is a compile time constant off the sp) be compiled
into
LD R0, y
ADD R0, R0, z
ST x, R0
But if we apply this to each quad separately (i.e., as a separate.
problem) then
LD R0, b
ADD R0, R0, c
ST a, R0
LD R0, a
ADD R0, e
ST d, R0
The fourth statement is clearly not needed since we are loading into
R0 the same value that it contains.
The inefficiency is caused by our compiling the second quad with no
knowledge of how we compiled the first quad.
Since registers are the fastest memory in the computer, the ideal solution is to store all values in registers. However, there are normally not nearly enough registers for this to be possible. So we must choose which values are in the registers at any given time.
Actually this problem has two parts.
The reason for the second problem is that often there are register requirements, e.g., floating-point values in floating-point registers and certain requirements for even-odd register pairs (e.g., 0&1 but not 1&2) for multiplication/division.
Sometimes better code results if the quads are reordered. One example occurs with modern processors that can execute multiple instructions concurrently, providing certain restrictions are met (the obvious one is that the input operands must already be evaluated).
This is a delicate compromise between RISC and CISC.
The goal is to be simple but to permit the study of nontrivial
addressing modes and the corresponding optimizations.
A charging
scheme is instituted to reflect that complex addressing
modes are not free.
We postulate the following (RISC-like) instruction set
Load. LD dest, addr loads the register dest with the contents of the address addr.
LD reg1, reg2 is a register copy.
A question is whether dest can be a memory location or whether it must be a register. This is part of the RISC/CISC debate. In CISC parlance, no distinction is made between load and store, both are examples of the general move instruction that can have an arbitrary source and an arbitrary destination.
We will normally not use a memory location for the destination of a load (or the target of a store). That is we do not permit memory to memory copy in one instruction.
As will be see below we charge more for a memory location than for a register.
The addressing modes are not RISC-like at first glance, as they permit memory locations to be operands. Again, note that we shall charge more for these.
Indexed address. The address a(r), where a is a variable name and r is a register (number) specifies the address that is, the value-in-r bytes past the address specified by a.
LD r1, a(r2) sets (the contents of R1) equal to
contents(a+contents(r2)) NOT
contents(contents(a)+contents(r2))
That is, the l-value of a and not the r-value is used.
If permitted outside a load or store instruction, this addressing mode would plant the CISC flag firmly in the ground.
For many quads the standard naive (RISC-like) translation is 4 instructions.
Array assignment statements are also four instructions. We can't do A[i]=B[j] because that needs four addresses.
The instruction x=A[i] becomes (assuming each element of A is 4 bytes)
LD R0, i
MUL R0, R0, #4
LD R0, A(R0)
ST x, R0
Similarly A[i]=x becomes
LD R0, x
LD R1, i
MUL R1, R1, #4
ST A(R1), R0
The pointer reference x = *p becomes
LD R0, p
LD R0, 0(R0)
ST x, R0
The assignment through a pointer *p = x becomes
LD R0, x
LD R1, p
ST 0(R1), R0
Finally if x < y goto L becomes
LD R0, x
LD R1, y
SUB R0, R0, R1
BNEG R0, L
The run-time cost of a program depends on (among other factors)
Here we just determine the first cost, and use quite a simple metric. We charge for each instruction one plus the cost of each addressing mode used.
Addressing modes using just registers have zero cost, while those involving memory addresses or constants are charged one. This corresponds to the size of the instruction since a memory address or a constant is assumed to be stored in a word right after the instruction word itself.
You might think that we are measuring the memory (or space) cost of the program not the time cost, but this is mistaken: The primary space cost is the size of the data, not the size of the instructions. One might say we are charging for the pressure on the I-cache.
For example, LD R0, *50(R2) costs 2, the additional cost is for the constant 50.
Homework: 9.1, 9.3
There are 4 possibilities for addresses that must be generated depending on which of the following areas the address refers to.
Returning to the glory days of Fortran, we consider a system with static allocation. Remember, that with static allocation we know before execution where all the data will be stored. There are no recursive procedures; indeed, there is no run-time stack of activation records. Instead the ARs are statically allocated by the compiler.
In this simplified situation, calling a parameterless procedure just
uses static addresses and can be implemented by two instructions.
Specifically,
call procA
can be implemented by
ST callee.staticArea, #here+20
BR callee.codeArea
We are assuming, for convenience, that the return address is the first location in the activation record (in general it would be a fixed offset from the beginning of the AR). We use the attribute staticArea for the address of the AR for the given procedure (remember again that there is no stack and heap).
What is the mysterious #here+20?
The # we know signifies an immediate constant. We use here to represent the address of the current instruction (the compiler knows this value since we are assuming that the entire program, i.e., all procedures, are compiled at once). The two instructions listed contain 3 constants, which means that the entire sequence takes 5 words or 20 bytes. Thus here+20 is the address of the instruction after the BR, which is indeed the return address.
With static allocation, the compiler knows the address of the the AR for the callee and we are assuming that the return address is the first entry. Then a procedure return is simply
BR *callee.staticArea
We consider a main program calling a procedure P and then
halting.
Other actions by Main and P are indicated by subscripted uses
of other
.
// Quadruples of Main other1 call P other2 halt // Quadruples of P other3 return
Let us arbitrarily assume that the code for Main starts in location 1000 and the code for P starts in location 2000 (there might be other procedures in between). Also assume that each otheri requires 100 bytes (all addresses are in bytes). Finally, we assume that the ARs for Main and P begin at 3000 and 4000 respectively. Then the following machine code results.
// Code for Main
1000: Other1
1100: ST 4000, #1120 // P.staticArea, #here+20
1112: BR 2000 // Two constants in previous instruction take 8 bytes
1120: other2
1220: HALT
...
// Code for P
2000: other3
2100: BR *4000
...
// AR for Main
3000: // Return address stored here (not used)
3004: // Local data for Main starts here
...
// AR for P
4000: // Return address stored here
4004: // Local data for P starts here
We now need to access the ARs from the stack. The key distinction is that the location of the current AR is not known at compile time. Instead a pointer to the stack must be maintained dynamically.
We dedicate a register, call it SP, for this purpose. In this chapter we let SP point to the bottom of the current AR, that is the entire AR is above the SP. (I do not know why last chapter it was decided to be more convenient to have the stack pointer point to the end of the statically known portion of the activation. However, since the difference between the two is known at compile time it is clear that either can be used.)
The first procedure (or the run-time library code called before
any user-written procedure) must initialize SP with
LD SP, #stackStart
were stackStart is a known-at-compile-time (even -before-) constant.
The caller increments SP (which now points to the beginning of its AR) to point to the beginning of the callee's AR. This requires an increment by the size of the caller's AR, which of course the caller knows.
Is this size a compile-time constant?
Both editions treat it as a constant. The only part that is not known at compile time is the size of the dynamic arrays. Strictly speaking this is not part of the AR, but it must be skipped over since the callee's AR starts after the caller's dynamic arrays.
Perhaps for simplicity we are assuming that there are no dynamic arrays being stored on the stack. If there are arrays, their size must be included in some way.
The code generated for a parameterless call is
ADD SP, SP, #caller.ARSize ST *SP, #here+16 // save return address BR callee.codeArea
The return requires code from both the Caller and Callee.
The callee transfers control back to the caller with
BR *0(SP)
upon return the caller restore the stack pointer with
SUB SP, SP, caller.ARSize
We again consider a main program calling a procedure P and then halting. Other actions by Main and P are indicated by subscripted uses of `other'.
// Quadruples of Main other[1] call P other[2] halt // Quadruples of P other[3] return
Recall our assumptions that the code for Main starts in location 1000, the code for P starts in location 2000, and each other[i] requires 100 bytes. Let us assume the stack begins at 9000 (and grows to larger addresses) and that the AR for Main is of size 400 (we don't need P.ARSize since P doesn't call any procedures). Then the following machine code results.
// Code for Main
1000; LD SP, 9000
1008: Other[1]
1108: ADD SP, SP, #400
1116: ST *SP, #1132
1124: BR, 2000
1132: SUB SP, SP, #400
1140: other[2]
1240: HALT
...
// Code for P
2000: other[3]
2100: BR *0(SP)
...
// AR for Main
9000: // Return address stored here (not used)
9004: // Local data for Main starts here
9396: // Last word of the AR is bytes 9396-9399
...
// AR for P
9400: // Return address stored here
9404: // Local data for P starts here
Basically skipped. A technical fine point about static allocation and (in 1e only) a corresponding point about the display.
Homework: 9.2
As we have seen, for may quads it is quite easy to generate a series of machine instructions to achieve the same effect. As we have also seen, the resulting code can be quite inefficient. For one thing the last instruction generated for a quad is often a store of a value that is then loaded right back in the next quad (or one or two quads later).
Another problem is that we don't make much use of the registers. That is translating a single quad needs just one or two registers so we might as well throw out all the other registers on the machine.
Both of the problems are due to the same cause: Our horizon is too limited. We must consider more than one quad at a time. But wild flow of control can make it unclear which quads are dynamically near each other. So we want to consider, at one time, a group of quads within which the dynamic order of execution is tightly controlled. We then also need to understand how execution proceeds from one group to another. Specifically the groups are called basic blocks and the execution order among them is captured by the flow graph.
Definition: A basic block is a maximal collection of consecutive quads such that
Definition: A flow graph has the basic blocks as vertices and has edges from one block to each possible dynamic successor.
Constructing the basic blocks is not hard. Once you find the start of a block, you keep going until you hit a label or jump. But, as usual, to say it correctly takes more words.
Definition: A basic block leader (i.e., first instruction) is any of the following (except for the instruction just past the entire program).
Given the leaders, a basic block starts with a leader and proceeds up to but not including the next leader.
The following code produces a 10x10 identity matrix
for i from 1 to 10 do
for j from 1 to 10 do
a[i,j] = 0
end
end
for i from 1 to 10 do
a[i,i] = 0
end
The following quads do the same thing
1) i = 1 2) j = 1 3) t1 = 10 * i 4) t2 = t1 + j // element [i,j] 5) t3 = 8 * t2 // offset for a[i,j] (8 byte numbers) 6) t4 = t3 - 88 // we start at [1,1] not [0,0] 7) a[t4] = 0.0 8) j = j + 1 9) if J <= 10 goto (3) 10) i = i + 1 11) if i <= 10 goto (2) 12) i = 1 13) t5 = i - 1 14) t6 = 88 * t5 15) a[t6] = 1.0 16) i = i + 1 17) if i <= 10 goto (13)
Which quads are leaders?
1 is a leader by definition. The jumps are 9, 11, and 17. So 10 and 12 are leaders as are the targets 3, 2, and 13.
The leaders are then 1, 2, 3, 10, 12, and 13.
The basic blocks are {1}, {2}, {3,4,5,6,7,8,9}, {10,11}, {12}, and {13,14,15,16,17}.
Here is the code written again with the basic blocks indicated.
1) i = 12) j = 13) t1 = 10 * i 4) t2 = t1 + j // element [i,j] 5) t3 = 8 * t2 // offset for a[i,j] (8 byte numbers) 6) t4 = t3 - 88 // we start at [1,1] not [0,0] 7) a[t4] = 0.0 8) j = j + 1 9) if J <= 10 goto (3)10) i = i + 1 11) if i <= 10 goto (2)12) i = 113) t5 = i - 1 14) t6 = 88 * t5 15) a[t6] = 1.0 16) i = i + 1 17) if i <= 10 goto (13)
We can see that once you execute the leader you are assured of executing the rest of the block in order.
We want to record the flow of information from instructions that compute a value to those that use the value. One advantage we will achieve is that if we find a value has no subsequent uses, then it is dead and the register holding that value can be used for another value.
Assume that a quad p assigns a value to x (some would call this a def of x).
Definition: Another quad q uses the value computed at p (uses the def) and x is live at q if q has x as an operand and there is a possible execution path from p to q that does not pass any other def of x.
Since the flow of control is trivial inside a basic block, we are able to compute the live/dead status and next use information for at the block leader by a simple backwards scan of the quads (algorithm below).
Note that if x is dead (i.e., not live) on entrance to B the register containing x can be reused in B.
Our goal is to determine whether a block uses a value and if so in which statement.
Initialize all variables in B as being live
Examine the quads of the block in reverse order.
Let the quad q compute x and read y and z
Mark x as dead; mark y and z as live and used at q
When the loop finishes those values that are read before being are marked as live and their first use is noted. The locations x that are set before being read are marked dead meaning that the value of x on entrance is not used.
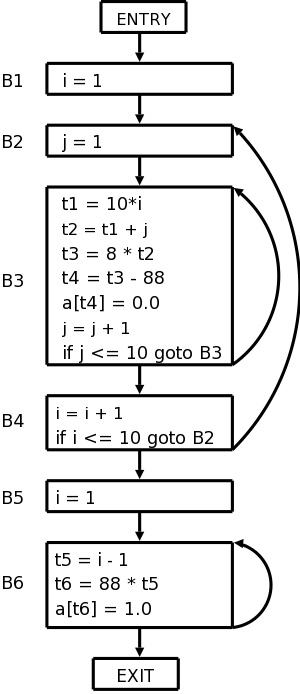
The nodes of the flow graph are the basic blocks and there is an edge from P (predecessor) to S (successor) if the last statement of P
Two nodes are added: entry
and exit
.
An edge is added from entry to the first basic block.
Edges to the exit are added from any block that could be the last block executed. Specifically edges are added from
The flow graph for our example is shown on the right.
Note that jump targets are no longer quads but blocks. The reason is that various optimizations within blocks will change the instructions and we would have to change the jump to reflect this.
Of course most of a program's execution time is within loops so we want to identify these.
Definition: A collection of basic blocks forms a loop L with loop entry E if
The flow graph on the right has three loops.
Homework: Consider the following program for matrix multiplication.
for (i=0; i<10; i++)
for (j=0; j<10; j++)
c[i][j] = 0;
for (i=0; i<10; i++)
for (j=0; j<10; j++)
for (k=0; k<10; k++)
c[i][j] = c[i][j] + a[i][k] * b[k][j];
We are not covering global flow analysis; it is a key component of optimization and would be a natural topic in a follow-on course. Nonetheless there is something we can say just by examining the flow graphs we have constructed. For this discussion I am ignoring tricky and important issues concerning arrays and pointer references (specifically, disambiguation). You may wish to assume that the program contains no arrays or pointers for these comments.
We have seen that a simple backwards scan of the statements in a
basic block enables us to determine the variables that are
live-on-entry and those that are dead-on-entry.
Those variables that do not occur in the block are in neither
category; perhaps we should call them ignored by the block
.
We shall see below that it would be lovely to know which variables are live/dead-on-exit. This means which variables hold values at the end of the block that will / will not be used. To determine the status of v on exit of a block B, we need to trace all possible execution paths beginning at the end of B. If all these paths reach a block where v is dead-on-entry before they reach a block where v is live-on-entry, then v is dead on exit for block B.
The goal is to obtain a visual picture of how information flows through the block. The leaves will show the values entering the block and as we proceed up the DAG we encounter uses of these values defs (and redefs) of values and uses of the new values.
Formally, this is defined as follows.
live on exit, an officially-mysterious term meaning values possibly used in another block. (Determining the live on exit values requires global, i.e., inter-block, flow analysis.)
As we shall see in the next few sections various basic-block
optimizations are facilitated by using the DAG.

As we create nodes for each statement, proceeding in the static order of the statements, we might notice that a new node is just like one already in the DAG in which case we don't need a new node and can use the old node to compute the new value in addition to the one it already was computing.
Specifically, we do not construct a new node if an existing node has the same children in the same order and is labeled with the same operation.
Consider computing the DAG for the following block of code.
a = b + c
c = a + x
d = b + c
b = a + x
The DAG construction is explain as follows (the movie on the right accompanies the explanation).
You might think that with only three computation nodes in the DAG,
the block could be reduced to three statements (dropping the
computation of b).
However, this is wrong.
Only if b is dead on exit can we omit the computation of b.
We can, however, replace the last statement with the simpler
b = c.
Sometimes a combination of techniques finds improvements that no
single technique would find.
For example if a-b is computed, then both a and b are incremented by
one, and then a-b is computed again, it will not be recognized as a
common subexpression even though the value has not changed.
However, when combined with various algebraic transformations, the
common value can be recognized.
Assume we are told (by global flow analysis) that certain values are dead on exit. We examine each root (node with no ancestor) and delete any that have no live variables attached. This process is repeated since new roots may have appeared.
For example, if we are told, for the picture on the right, that only a and b are live, then the root d can be removed since d is dead. Then the rightmost node becomes a root, which also can be removed (since c is dead).
Some of these are quite clear. We can of course replace x+0 or 0+x by simply x. Similar considerations apply to 1*x, x*1, x-0, and x/1.
Another class of simplifications is strength reduction, where we replace one operation by a cheaper one. A simple example is replacing 2*x by x+x on architectures where addition is cheaper than multiplication.
A more sophisticated strength reduction is applied by compilers that
recognize induction variables
(loop indices).
Inside a
for i from 1 to N
loop, the expression 4*i can be strength reduced to j=j+4 and 2^i
can be strength reduced to j=2*j (with suitable initializations of j
just before the loop).
Other uses of algebraic identities are possible; many require a
careful reading of the language reference manual to ensure their
legality.
For example, even though it might be advantageous to convert
((a + b) * f(x)) * a
to
((a + b) * a) * f(x)
it is illegal in Fortran since the programmer's use of parentheses
to specify the order of operations can not be violated.
Does
a = b + c
x = y + c + b + r
contain a common subexpression of b+c that need be evaluated only
once?Arrays are tricky. Question: Does
x = a[i]
a[j] = 3
z = a[i]
contain a common subexpression of a[i] that need be evaluated only
once?A statement of the form x = a[i] generates a node labeled with the operator =[] and the variable x, and having children a0, the initial value of a, and the value of i.
A statement of the form a[j] = y generates a node labeled with operator []= and three children a0. j, and y, but with no variable as label. The new feature is that this node kills all existing nodes depending on a0. A killed node can not received any future labels so cannot becomew a common subexpression.
Returning to our example
x = a[i]
a[j] = 3
z = a[i]
We obtain the top figure to the right.
Sometimes it is not children but grandchildren (or other descendant) that are arrays. For example we might have
b = a + 8 // b[i] is 8 bytes past a[i]
x = b[i]
b[j] = y
Again we need to have the third statement kill the second node even
though it is caused by a grandchild.
This is shown in the bottom figure.
Pointers are even trickier than arrays.
Together they have spawned a mini-industry in disambiguation
,
i.e., when can we tell whether two array or pointer references refer
to the same or different locations.
A trivial case of disambiguation occurs with.
p = &x
*p = y
In this case we know precisely the value of p so the second
statement kills only nodes with x attached.
With no disambiguation information, we must assume that a pointer can refer to any location. Consider
x = *p
*q = y
We must treat the first statement as a use of every variable; pictorially the =* operator takes all current nodes with identifiers as arguments. This impacts dead code elimination.
We must treat the second statement as writing every variable. That is all existing nodes are killed, which impacts common subexpression elimination.
In our basic-block level approach, a procedure call has properties similar to a pointer reference: For all x in the scope of P, we must treat a call of P as using all nodes with x attached and also kills those same nodes.
Now that we have improved the DAG for a basic block, we need to regenerate the quads. That is, we need to obtain the sequence of quads corresponding to the new DAG.
We need to construct a quad for every node that has a variable attached. If there are several variables attached we chose a live-on-exit variable, assuming we have done the necessary global flow analysis to determine such variables).
If there are several live-on-exit variables we need to compute one and make a copy so that we have both. An optimization pass may eliminate the copy if it is able to assure that one such variable may be used whenever the other is referenced.
Recall the example from our movie
a = b + c
c = a + x
d = b + c
b = a + x
If b is dead on exit, the first three instructions suffice. If not we produce instead
a = b + c
c = a + x
d = b + c
b = c
which is still an improvement as the copy instruction is less
expensive than the addition on most architectures.
If global analysis shows that, whenever this definition of b is used, c contains the same value, we can eliminate the copy and use c in place of b.
Note that of the following 5, rules 2 are due to arrays, and 2 due to pointers.
Homework: 9.14,
9.15 (just simplify the 3-address code of 9.14 using the two cases
given in 9.15), and
9.17 (just construct the DAG for the given basic block in the two
cases given).
A big issue is proper use of the registers, which are often in short supply, and which are used/required for several purposes.
For this section we assume a RISC architecture. Specifically, we assume only loads and stores touch memory; that is, the instruction set consists of
LD reg, mem
ST mem, reg
OP reg, reg, reg
where there is one OP for each operation type used in the three
address code.
The 1e uses CISC like instructions (2 operands). Perhaps 2e switched to RISC in part due to the success of the ROPs in the Pentium Pro.
A major simplification is we assume that, for each three address operation, there is precisely one machine instruction that accomplishes the task. This eliminates the question of instruction selection.
We do, however, consider register usage. Although we have not done global flow analysis (part of optimization), we will point out places where live-on-exit information would help us make better use of the available registers.
Recall that the mem operand in the load LD and store ST
instructions can use any of the previously discussed addressing
modes.
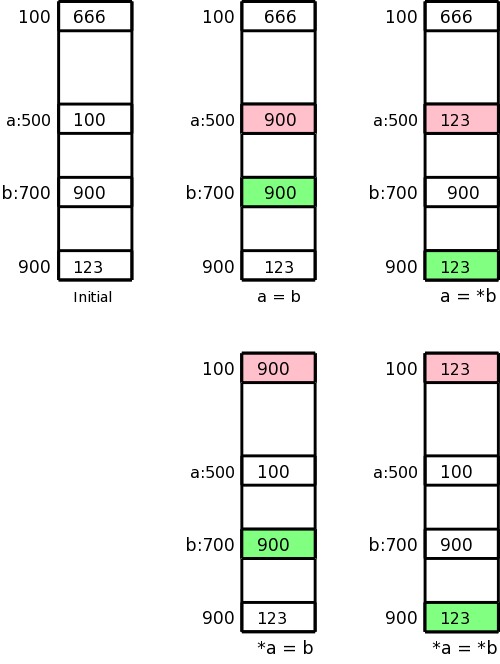
Remember that in 3-address instructions, the variables written are addresses, i.e., they represent l-values.
Let us assume a is 500 and b is 700, i.e., a and b refer to locations 500 and 700 respectively. Assume further that location 100 contains 666, location 500 contains 100, location 700 contains 900, and location 900 contains 123. This initial state is shown in the upper left picture.
In the four other pictures the contents of the pink location has been changed to the contents of the light green location. These correspond to the three-address assignment statements shown below each picture. The machine instructions indicated below implement each of these assignment statements.
a = b
LD R1, b
ST a, R1
a = *b
LD R1, b
LD R1, 0(R1)
ST a, R1
*a = b
LD R1, b
LD R2, a
ST 0(R2), R1
*a = *b
LD R1, b
LD R1, 0(R1)
LD R2, a
ST 0(R2), R1
These are the primary data structures used by the code generator. They keep track of what values are in each register as well as where a given value resides.
The register descriptor could be omitted since you can compute it from the address descriptors.
There are basically three parts to (this simple algorithm for) code generation.
We will isolate register allocation in a function getReg(Instruction), which is presented later. First presented is the algorithm to generate instructions. This algorithm uses getReg() and the descriptors. Then we learn how to manage the descriptors and finally we study getReg() itself.
Given a quad OP x, y, z (i.e., x = y OP z), proceed as follows.
Call getReg(OP x, y, z) to get Rx, Ry, and Rz, the registers to be used for x, y, and z respectively.
Note that getReg merely selects the registers, it does not guarantee that the desired values are present in these registers.
Check the register descriptor for Ry.
If y is not present in Ry, check the address descriptor
for y and issue
LD Ry, y
The 2e uses y' (not y) as source of the load, where y' is some location containing y (1e suggests this as well). I don't see how the value of y can appear in any memory location other than y. Please check me on this.
One might worry that either
It would be a serious bug in the algorithm if the first were
true, and I am confident it is not.
The second might be a possible design, but when we study
getReg(), we will see that if the value of y is in some
register, then the chosen Ry will contain that
value.
When processing
x = y
steps 1 and 2 are the same as above
(getReg() will set Rx=Ry).
Step 3 is vacuous and step 4 is omitted.
This says that if y was already in a register before the copy
instruction, no code is generated at this point.
Since the value of y is not in its memory location,
we may need to store this value back into y at block exit.
You probably noticed that we have not yet generated any store instructions; They occur here (and during spill code in getReg()). We need to ensure that all variables needed by (dynamically) subsequent blocks (i.e., those live-on-exit) have their current values in their memory locations.
All live on exit variables (for us all non-temporaries) need to be in their memory location on exit from the block.
Check the address descriptor for each live on exit variable.
If its own memory location is not listed, generate
ST x, R
where R is a register listed in the address descriptor
This is fairly clear. We just have to think through what happens when we do a load, a store, an OP, or a copy. For R a register, let Desc(R) be its register descriptor. For x a program variable, let Desc(x) be its address descriptor.
Since we haven't specified getReg() yet, we will assume there are an unlimited number of registers so we do not need to generate any spill code (saving the register's value in memory). One of getReg()'s jobs is to generate spill code when a register needs to be used for another purpose and the current value is not presently in memory.
Despite having ample registers and thus not generating spill code, we will not be wasteful of registers.
This example is from the book. I give another example after presenting getReg(), that I believe justifies my claim that the book is missing an action, as indicated above.
Assume a, b, c, and d are program variables and t, u, v are compiler generated temporaries (I would call these t$1, t$2, and t$3). The intermediate language program is on the left with the generated code for each quad shown. To the right is shown the contents of all the descriptors. The code generation is explained below the diagram.

t = a - b
LD R1, a
LD R2, b
SUB R2, R1, R2
u = a - c
LD r3, c
SUB R1, R1, R3
v = t + u
ADD R3, R2, R1
a = d
LD R2, d
d = v + u
ADD R1, R3, R1
exit
ST a, R2
ST d, R1
What follows describes the choices made. Confirm that the values in the descriptors matches the explanations.
Consider
x = y OP z
Picking registers for y and z are the same; we just do y.
Choosing a register for x is a little different.
A copy instruction
x = y
is easier.
Similar to demand paging, where the goal is to produce an available frame, our objective here is to produce an available register we can use for Ry. We apply the following steps in order until one succeeds. (Step 2 is a special case of step 3.)
As stated above choosing Rz is the same as choosing Ry.
Choosing Rx has the following differences.
getReg(x=y) chooses Ry as above and chooses Rx=Ry.
R1 R2 R3 a b c d e
a b c d e
a = b + c
LD R1, b
LD R2, c
ADD R3, R1, R2
R1 R2 R3 a b c d e
b c a R3 b,R1 c,R2 d e
d = a + e
LD R1, e
ADD R2, R3, R1
R1 R2 R3 a b c d e
2e → e d a R3 b,R1 c R2 e,R1
me → e d a R3 b c R2 e,R1
We needed registers for d and e; none were free. getReg() first chose R2 for d since R2's current contents, the value of c, was also located in memory. getReg() then chose R1 for e for the same reason.
Using the 2e algorithm, b might appear to be in R1 (depends if you look in the address or register descriptors).
a = e + d
ADD R3, R1, R2
Descriptors unchanged
e = a + b
ADD R1, R3, R1 ← possible wrong answer from 2e
R1 R2 R3 a b c d e
e d a R3 b,R1 c R2 R1
LD R1, b
ADD R1, R3, R1
R1 R2 R3 a b c d e
e d a R3 b c R2 R1
The 2e might think R1 has b (address descriptor) and also conclude R1 has only e (register descriptor) so might generate the erroneous code shown.
Really b is not in a register so must be loaded. R3 has the value of a so was already chosen for a. R2 or R1 could be chosen. If R2 was chosen, we would need to spill d (we must assume live-on-exit, since we have no global flow analysis). We choose R1 since no spill is needed: the value of e (the current occupant of R1) is also in its memory location.
exit
ST a, R3
ST d, R2
ST e, R1
Skipped.
Skipped.
What if a given quad needs several OPs and we have choices?
We would like to be able to describe the machine OPs in a way that enables us to find a sequence of OPs (and LDs and STs) to do the job.
The idea is that you express the quad as a tree and express each OP
as a (sub-)tree simplification, i.e. the op replaces a subtree by a
simpler subtree.
In fact the simpler subtree is just a single node.
The diagram on the right represents x[i] = y[a] + 9, where x and y are on the stack and a is in the static area. M's are values in memory; C's are constants; and R's are registers. The weird ind (presumably short for indirect) treats its argument as a memory location.
Compare this to grammars: A production replaces the RHS by the LHS. We consider context free grammars where the LHS is a single nonterminal.
For example, a LD replaces a Memory node with a Register node.
Another example is that ADD Ri, Ri, Rj replaces a subtree consisting of a + with both children registers (i and j) with a Register node (i).
As you do the pattern matching and reductions (apply the productions), you emit the corresponding code (semantic actions). So to support a new processor, you need to supply the tree transformations corresponding to every instruction in the instruction set.
This is quite cute.
We assume all operators are binary and label the instruction tree with something like the height. This gives the minimum number of registers needed so that no spill code is required. A few details follow.
biggerchild L regs.
Can see this is optimal (assuming you have enough registers).
Rough idea is to apply the above recursive algorithm, but at each recursive step, if the number of regs is not enough, store the result of the first child computed before starting the second.
Skipped