Operating Systems
================ Start Lecture #9 ================
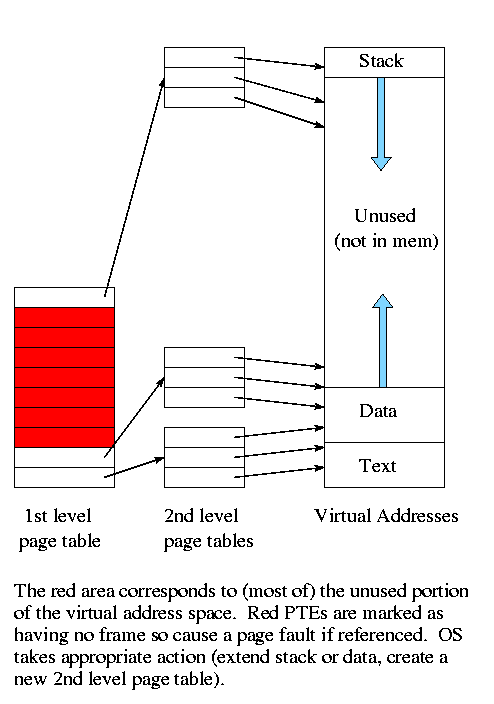
Multilevel page tables
Recall the previous diagram. Most of the virtual memory is the
unused space between the data and stack regions. However, with demand
paging this space does not waste real memory. But the single
large page table does waste real memory.
The idea of multi-level page tables (a similar idea is used in Unix
i-node-based file systems, which we study later) is to add a level of
indirection and have a page table containing pointers to page tables.
-
Imagine one big page table.
-
Call it the second level page table and
cut it into pieces each the size of a page.
Note that many (typically 1024 or 2048) PTEs fit in one page so
there are far fewer of these pages than PTEs.
-
Now construct a first level page table containing PTEs that
point to these pages.
-
This first level PT is small enough to store in memory. It
contains one PTE for every page of PTEs in the 2nd level PT. A
space reduction of one or two thousand.
-
But since we still have the 2nd level PT, we have made the world
bigger not smaller!
-
Don't store in memory those 2nd level page tables all of whose PTEs
refer to unused memory. That is use demand paging on the (second
level) page table
Address translation with a 2-level page table
For a two level page table the virtual address is divided into
three pieces
+-----+-----+-------+
| P#1 | P#2 | Offset|
+-----+-----+-------+
-
P#1 gives the index into the first level page table.
-
Follow the pointer in the corresponding PTE to reach the frame
containing the relevant 2nd level page table.
-
P#2 gives the index into this 2nd level page table
-
Follow the pointer in the corresponding PTE to reach the frame
containing the (originally) requested frame.
-
Offset gives the offset in this frame where the requested word is
located.
Do an example on the board
The VAX used a 2-level page table structure, but with some wrinkles
(see Tanenbaum for details).
Naturally, there is no need to stop at 2 levels. In fact the SPARC
has 3 levels and the Motorola 68030 has 4 (and the number of bits of
Virtual Address used for P#1, P#2, P#3, and P#4 can be varied).
4.3.3: TLBs--Translation Lookaside Buffers (and General
Associative Memory)
Note:
Tanenbaum suggests that “associative memory” and “translation
lookaside buffer” are synonyms. This is wrong. Associative memory
is a general concept and translation lookaside buffer is a special
case.
An associative memory is a
content addressable memory.
That is you access the memory by giving the value
of some (index) field and the hardware searches all the records and returns
the record whose field contains the requested value.
For example
Name | Animal | Mood | Color
======+========+==========+======
Moris | Cat | Finicky | Grey
Fido | Dog | Friendly | Black
Izzy | Iguana | Quiet | Brown
Bud | Frog | Smashed | Green
If the index field is Animal and Iguana is given, the associative
memory returns
Izzy | Iguana | Quiet | Brown
A Translation Lookaside Buffer
or TLB
is an associate memory
where the index field is the page number. The other fields include
the frame number, dirty bit, valid bit, etc.
-
A TLB is small and expensive but at least it is
fast. When the page number is in the TLB, the frame number
is returned very quickly.
-
On a miss, the page number is looked up in the page table. The record
found is placed in the TLB and a victim is discarded. There is no
placement question since all entries are accessed at the same time.
But there is a replacement question.
Homework: 17.
4.3.4: Inverted page tables
Keep a table indexed by frame number. The content of entry f contains the
number of the page currently loaded in frame f.
This is often called a frame table as well as an inverted page
table.
-
Since modern machine have a smaller physical address space than
virtual address space, the frame table is smaller than the
corresponding page table.
-
But on a TLB miss, the system must search the inverted
page table.
-
Would be hopelessly slow except that some tricks are employed.
-
The book mentions some but not all of the tricks, we are not
covering the tricks.
-
For us, the frame table would be searched on each TLB miss.
-
Of course you can use both a frame table and a page table.
4.4: Page Replacement Algorithms (PRAs)
These are solutions to the replacement question.
Good solutions take advantage of locality.
-
Temporal locality: If a word is referenced now,
it is likely to be referenced in the near future.
-
This argues for caching referenced words,
i.e. keeping the referenced word near the processor for a while.
-
Spatial locality: If a word is referenced now,
nearby words are likely to be referenced in the near future.
-
This argues for prefetching words around the currently
referenced word.
-
These are lumped together into locality: If any
word in a page is referenced, each word in the page is
“likely” to be referenced.
-
So it is good to bring in the entire page on a miss and to
keep the page in memory for a while.
-
When programs begin there is no history so nothing to base
locality on. At this point the paging system is said to be undergoing
a “cold start”.
-
Programs exhibit “phase changes”, when the set of
pages referenced changes abruptly (similar to a cold start). At
the point of a phase change, many page faults occur because
locality is poor.
Pages belonging to processes that have terminated are of course
perfect choices for victims.
Pages belonging to processes that have been blocked for a long time
are good choices as well.
Random PRA
A lower bound on performance. Any decent scheme should do better.
4.4.1: The optimal page replacement algorithm (opt PRA) (aka
Belady's min PRA)
Replace the page whose next
reference will be furthest in the future.
-
Also called Belady's min algorithm.
-
Provably optimal. That is, generates the fewest number of page
faults.
-
Unimplementable: Requires predicting the future.
-
Good upper bound on performance.
4.4.2: The not recently used (NRU) PRA
Divide the frames into four classes and make a random selection from
the lowest nonempty class.
-
Not referenced, not modified
-
Not referenced, modified
-
Referenced, not modified
-
Referenced, modified
Assumes that in each PTE there are two extra flags R (sometimes called
U, for used) and M (often called D, for dirty).
Also assumes that a page in a lower priority class is cheaper to evict.
-
If not referenced, probably will not referenced again soon and
hence is a good candidate for eviction.
-
If not modified, do not have to write it out so the cost of the
eviction is lower.
-
When a page is brought in, OS resets R and M (i.e. R=M=0)
-
On a read, hardware sets R.
-
On a write, hardware sets R and M.
We again have the prisoner problem, we do a good job of making little
ones out of big ones, but not the reverse. Need more resets.
Every k clock ticks, reset all R bits
-
Why not reset M?
Answer: Must have M accurate to know if victim needs to be written back
-
Could have two M bits one accurate and one reset, but I don't know
of any system (or proposal) that does so.
What if the hardware doesn't set these bits?
-
OS can use tricks
-
When the bits are reset, make the PTE indicate the page is not
resident (i.e. lie). On the page fault, set the appropriate
bit(s).
-
We ignore the tricks and assume the hardware does set the bits.
4.4.3: FIFO PRA
Simple but poor since usage of the page is ignored.
Belady's Anomaly: Can have more frames yet generate
more faults.
Example given later.
The natural implementation is to have a queue of nodes each
pointing to a page.
-
When a page is loaded, a node referring to the page is appended to
the tail of the queue.
-
When a page needs to be evicted, the head node is removed and the
page referenced is chosen as the victim.
4.4.4: Second chance PRA
Similar to the FIFO PRA, but altered so that a page recently
referenced is given a second chance.
-
When a page is loaded, a node referring to the page is appended to
the tail of the queue. The R bit of the page is cleared.
-
When a page needs to be evicted, the head node is removed and the
page referenced is the potential victim.
-
If the R bit on this page is unset (the page hasn't been
referenced recently), then the page is the victim.
-
If the R bit is set, the page is given a second chance.
Specifically, the R bit is cleared, the node
referring to this page is appended to the rear of the queue (so it
appears to have just been loaded), and the current head node
becomes the potential victim.
-
What if all the R bits are set?
-
We will move each page from the front to the rear and will arrive
at the initial condition but with all the R bits now clear. Hence
we will remove the same page as fifo would have removed, but will
have spent more time doing so.
-
Might want to periodically clear all the R bits so that a long ago
reference is forgotten (but so is a recent reference).
4.4.5: Clock PRA
Same algorithm as 2nd chance, but a better
implementation for the nodes: Use a circular list with a single
pointer serving as both head and tail.
Let us begin by assuming that the number of pages loaded is
constant.
-
So the size of the node list in 2nd chance is constant.
-
Use a circular list for the nodes and have a pointer pointing to
the head entry. Think of the list as the hours on a clock and the
pointer as the hour hand.
-
Since the number of nodes is constant, the operation we need to
support is replace the “oldest” page by a new page.
-
Examine the node pointed to by the (hour) hand.
If the R bit of the corresponding page is set, we give the
page a second chance: clear the R bit, move the hour hand (now the page
looks freshly loaded), and examine the next node.
-
Eventually we will reach a node whose corresponding R bit is
clear. The corresponding page is the victim.
-
Replace the victim with the new page (may involve 2 I/Os as
always).
-
Update the node to refer to this new page.
-
Move the hand forward another hour so that the new page is at the
rear.
What if the number of pages is not constant?
-
We now have to support inserting a node right before
the hour hand (the rear of the queue) and removing the node
pointed to by the hour hand.
-
The natural solution is to double link the circular list.
-
In this case insertion and deletion are a little slower than for
the primitive 2nd chance (double linked lists have more pointer
updates for insert and delete).
-
So the trade-off is that if there are mostly inserts and deletes
and granting 2nd chances is not too common, use the original 2nd
chance implementation.
If there are mostly replacements and you
often give nodes a 2nd chance, use clock.
LIFO PRA
This is terrible! Why?
Ans: All but the last frame are frozen once loaded so you can replace
only one frame. This is especially bad after a phase shift in the
program when it is using all new pages.
4.4.6: Least Recently Used (LRU) PRA
When a page fault occurs, choose as victim that page that has been
unused for the longest time, i.e. that has been least recently used.
LRU is definitely
-
Implementable: The past is knowable.
-
Good: Simulation studies have shown this.
-
Difficult. Essentially need to either:
-
Keep a time stamp in each PTE, updated on each reference
and scan all the PTEs when choosing a victim to find the PTE
with the oldest timestamp.
-
Keep the PTEs in a linked list in usage order, which means
on each reference moving the PTE to the end of the list
| Page | Loaded | Last ref. | R | M
|
|---|
| 0 | 126 | 280 | 1 | 0
|
| 1 | 230 | 265 | 0 | 1
|
| 2 | 140 | 270 | 0 | 0
|
| 3 | 110 | 285 | 1 | 1
|
Homework: 29, 23.
Note: there is a typo in 29; the table should be as shown on the right.
A hardware cutsie in Tanenbaum
-
For n pages, keep an nxn bit matrix.
-
On a reference to page i, set row i to all 1s and col i to all 0s
-
At any time the 1 bits in the rows are ordered by inclusion.
I.e. one row's 1s are a subset of another row's 1s, which is a
subset of a third. (Tanenbaum forgets to mention this.)
-
So the row with the fewest 1s is a subset of all the others and is
hence least recently used.
-
This row also has the smallest value, when treated as an unsigned
binary number. So the hardware can do a comparison of the rows
rather than counting the number of 1 bits.
-
Cute, but still impractical.
4.4.7: Simulating (Approximating) LRU in Software
The Not Frequently Used (NFU) PRA
-
Include a counter in each PTE (and have R in each PTE).
-
Set counter to zero when page is brought into memory.
-
For each PTE, every k clock ticks.
-
Add R to counter.
-
Clear R.
-
Choose as victim the PTE with lowest count.
| R | counter |
|---|
| 1 | 10000000 |
|
| 0 | 01000000 |
|
| 1 | 10100000 |
|
| 1 | 11010000 |
|
| 0 | 01101000 |
|
| 0 | 00110100 |
|
| 1 | 10011010 |
|
| 1 | 11001101 |
|
| 0 | 01100110 |
|
The Aging PRA
NFU doesn't distinguish between old references and recent ones. The
following modification does distinguish.
-
Include a counter in each PTE (and have R in each PTE).
-
Set counter to zero when page is brought into memory.
-
For each PTE, every k clock ticks.
- Shift counter right one bit.
- Insert R as new high order bit (HOB).
- Clear R.
-
Choose as victim the PTE with lowest count.
Homework: 25, 34
4.4.8: The Working Set Page Replacement Problem (Peter Denning)
The working set policy (Peter Denning)
The goal is to specify which pages a given process needs to have
memory resident in order for the process to run without too many
page faults.
-
But this is impossible since it requires predicting the future.
-
So we make the assumption that the immediate future is well
approximated by the immediate past.
-
We measure time in units of memory references, so t=1045 means the
time when the 1045th memory reference is issued.
-
In fact we measure time separately for each process, so t=1045
really means the time when this process made its 1045th memory
reference.
-
W(t,&omega) is the set of pages referenced (by the given process) from
time t-ω to time t.
-
That is, W(t,ω) is the set pages referenced during
the window of size ω ending at time t.
-
That is, W(t,ω) is the set of pages referenced by the last
ω memory references ending at reference t.
-
W(t,ω) is called the working set at time t
(with window ω).
-
w(t,ω) is the size of the set W(t,ω), i.e. is the
number of distinct pages referenced in the window.
The idea of the working set policy is to ensure that each process
keeps its working set in memory.
-
Allocate w(t,ω) frames to each process.
This number differs for each process and changes with time.
-
On a fault, one evicts a page not in the working set. But it is
not easy to find such a page quickly.
-
Indeed determining W(t,ω) precisely is quite time consuming
and difficult. It is never done in real systems.
-
If a process is suspended, it is often swapped out; the working
set then can be used to say which pages should be brought back
when the process is resumed.
Homework: Describe a process (i.e., a program)
that runs for a long time (say hours) and always has w<10
Assume ω=100,000, the page size is 4KB. The program need not be
practical or useful.
Homework: Describe a process that runs for a long
time and (except for the very beginning of execution) always has
w>1000. Assume ω=100,000, the page size is 4KB. The program
need not be practical or useful.
The definition of Working Set is local to a process. That is, each
process has a working set; there is no system wide working set other
than the union of all the working sets of each process.
However, the working set of a single process has effects on the
demand paging behavior and victim selection of other processes.
If a process's working set is growing in size, i.e. w(t,ω) is
increasing as t increases, then we need to obtain new frames from
other processes. A process with a working set decreasing in size is a
source of free frames. We will see below that this is an interesting
amalgam of
local and global replacement policies.
Interesting questions concerning the working set include:
-
What value should be used for ω?
Experiments have been done and ω is surprisingly robust (i.e.,
for a given system, a fixed value works reasonably for a wide variety
of job mixes).
-
How should we calculate W(t,ω)?
Hard so do exactly so ...
... Various approximations to the working set, have been devised.
We will study two: using virtual time instead of memory references
(immediately below) and Page Fault Frequency (section 4.6).
In 4.4.9 we will see the popular WSClock algorithm that includes an
approximation of the working set as well as several other ideas.
Using virtual time
-
Approximate the working set by those pages referenced during the
last m milliseconds rather than the last ω memory references.
Note that the time is measured only while this process is running,
i.e., we are using virtual time.
-
Clear the reference bit every m milliseconds and set it on every
reference.
-
To choose a victim, we need to find a page with the R bit
clear.
-
Essentially we have reduced the working set policy to NRU.

