================ Start Lecture #1 ================
Basic Algorithms
2004-05 Fall
Tues/Thurs 11-12:15
Chapter 0 Administrivia
I start at 0 so that when we get to chapter 1, the numbering will
agree with the text.
0.1 Contact Information
- gottlieb@nyu.edu (best method)
- http://cs.nyu.edu/~gottlieb
- 715 Broadway, Room 712
0.2 Course Web Page
There is a web site for the course.
You can find it from my home page.
-
You can find these lecture notes on the course home page.
Please let me know if you can't find it.
-
The notes will be updated as bugs are found.
-
I will also produce a separate page for each lecture after the
lecture is given. These individual pages
might not get updated as quickly as the large page
0.3 Textbook
The course text is Goodrich and Tamassia: ``Algorithm Design:
Foundations, Analysis, and Internet Examples.
-
Available in bookstore.
-
I expect to cover much of part I and some of part II.
0.4 Computer Accounts and Mailman Mailing List
-
You are entitled to a computer account, please get it asap.
-
Sign up for the Mailman mailing list for the course.
http://www.cs.nyu.edu/mailman/listinfo/v22_0310_002_fa04.
Note that replies are sent to the list.
-
If you want to send mail just to me, use gottlieb AT nyu.edu not
the mailing list.
-
Questions about the lectures or homeworks should go to the mailing
list.
You may answer questions posed on the list as well.
-
I will respond to all questions; if another student has answered the
question before I get to it, I will confirm if the answer given is
correct.
0.5 Grades
The grades is computed as
30% midterm, 30% problem sets, 40% final exam.
0.6 Midterm
We will have a midterm. As the time approaches we will vote in
class for the exact date. Please do not schedule any trips during
days when the class meets until the midterm date is scheduled.
0.7 Homeworks, Problem Sets, and Labs
If you had me for 202, you know that in systems courses I also
assign labs. Basic algorithms is not a systems
course; there are no labs. There are homeworks and problem sets,
very few if any of these will require the computer. There is a
distinction between homeworks and problem sets.
Problem sets are
-
Required.
-
Due several lectures later (date given on assignment).
-
Graded and form part of your final grade.
-
Penalized for lateness, up to one week.
Homeworks are
-
Optional.
-
Due the beginning of Next lecture.
-
Not accepted late.
-
Mostly from the book.
-
Collected and returned.
-
Able to help, but not hurt, your grade.
0.8 Recitation
I run a recitation session on Tuesdays from 2-3:15 in room 102.
There is another session on Thursdays from 9:30-10-45 in room 109.
You should only attend one.
0.9 Obtaining Help
Good methods for obtaining help include
-
Asking me during office hours (see web page for my hours).
-
Asking the mailing list.
-
Asking another student, but ...
Your homeworks and problem sets must be your own.
0.10 The Upper Left Board
I use the upper left board for homework assignments and
announcements. I should never erase that board.
Viewed as a file it is group readable (the group is those in the
room), appendable by just me, and (re-)writable by no one.
If you see me start to erase an announcement, let me know.
0.11 A Grade of ``Incomplete''
It is university policy that a student's request for an incomplete
be granted only in exceptional circumstances and only if applied for
in advance. Naturally, the application must be before the final exam.
Part I: Fundamental Tools
Chapter 1 Algorithm Analysis
We are interested in designing good
algorithms (a step-by-step procedure for performing
some task in a finite amount of time) and good
data structures (a systematic way of organizing and
accessing data).
Unlike v22.102, however, we wish to determine rigorously just
how good our algorithms and data structures really
are and whether significantly better algorithms are
possible.
1.1 Methodologies for Analyzing Algorithms
We will be primarily concerned with the speed (time
complexity) of algorithms.
-
Sometimes the space complexity is studied.
-
The time depends on the input, often on just the amount of
input. For example, the time required to sum N numbers depends on
N but not on the numbers themselves (we assume all values fit in
one computer word).
-
One could run experiments in order to determine the space complexity.
-
Must choose sufficiently many, representative inputs.
-
Must use identical hardware to compare algorithms.
-
Must implement the algorithm.
We will emphasize instead an analytic framework that is independent
of input and hardware, and does not require an implementation. The
disadvantage is that we can only estimate the time required.
-
Often we ignore multiplicative constants and small input values.
-
So we consider f(x)=x3-20x2
equivalent to g(x)=10x3+10x2
-
Huh??
-
Easy to see that for say x > 100, f(x) < 10 g(x) and
g(x) < 10 f(x).
Homework: R-1.1 and R-1.2
(Unless otherwise stated, homework
problems are from the last section in the current book chapter.)
1.1.1 Pseudo-Code
Designed for human understanding. Suppress unimportant details and
describe some parts in natural language (English in this course).
1.1.2 The Random Access Machine (RAM) Model
The key difference between the RAM model and a real computer is the
assumption of a very simple memory model: Accessing any memory element
takes a constant amount of time. This ignores caching and paging for
example. (It also assumes
the word-size of a computer is large enough to hold any address, which
is generally valid for modern-day computers, but was not always the case.)
The time required is simply a count of the primitive
operations executed.
A more sophisticated analysis might count some primitive operations as
more expensive than others.
There are many possible
sets of primitive operations. For this course we will use
- Assigning a value to a variable (independent of the size of the
value; but the variable must be a scalar).
- Method invocation, i.e., calling a function or subroutine.
- Performing a (simple) arithmetic operation (divide is OK,
logarithm is not).
- Indexing into an array (for now just one dimensional; scalar
access is free).
- Following an object reference.
- Returning from a method.
1.1.3 Counting Primitive Operations
Let's start with a simple algorithm (the book does a different
simple algorithm, maximum).
Algorithm innerProduct
Input: Non-negative integer n and two integer arrays A and B of size n.
Output: The inner product of the two arrays.
prod ← 0
for i ← 0 to n-1 do
prod ← prod + A[i]*B[i]
return prod
- Line 1 is one op (assigning a value).
- Loop initializing is one op (assigning a value).
- Line 3 is five ops per iteration (mult, add, 2 array refs, assign).
- Line 3 is executed n times; total is 5n.
- Loop incrementation is two ops (an addition and an assignment)
- Loop incrementation is done n times; total is 2n.
- Loop termination test is one op (a comparison i<n).
- Loop termination is done n+1 times (n successes, one failure);
total is n+1.
- Return is one op.
The total is thus 1+1+5n+2n+(n+1)+1 = 8n+4.
Homework: Perform a similar analysis for
the following algorithm
Algorithm tripleProduct
Input: Non-negative integer n and three integer arrays A. B, and C
each of size n.
Output: The sum A[0]*B[0]*C[0] + ... + A[n-1]*B[n-1]*C[n-1]
prod ← 0
for i ← 0 to n-1 do
prod ← prod + A[i]*B[i]*C[i]
return prod
End of homework
Let's speed up innerProduct (a very little bit).
Algorithm innerProductBetter
Input: Non-negative integer n and two integer arrays A and B of size n.
Output: The inner product of the two arrays
prod ← A[0]*B[0]
for i ← 1 to n-1 do
prod ← prod + A[i]*B[i]
return prod
The cost is 4+1+5(n-1)+2(n-1)+n+1 = 8n-1
THIS ALGORITHM IS WRONG!!
If n=0, we access A[0] and B[0], which do not exist. The original
version returns zero as the inner product of empty arrays, which is
arguably correct. The best fix is perhaps to change Non-negative
to Positive
in the Input specification.
Let's call this algorithm innerProductBetterFixed.
What about if statements?
Algorithm countPositives
Input: Non-negative integer n and an integer array A of size n.
Output: The number of positive elements in A
pos ← 0
for i ← 0 to n-1 do
if A[i] > 0 then
pos ← pos + 1
return pos
-
Line 1 is one op.
-
Loop initialization is one op
-
Loop termination test is n+1 ops
-
The if test is performed n times; each is 2 ops
-
Return is one op
-
The update of pos is 2 ops but is done ??? times.
-
What do we do?
Let U be the number of updates done.
-
The total number of steps is 1+1+(n+1)+2n+1+2U = 4+3n+2U.
-
The best case (i.e., lowest complexity) occurs
when U=0 (i.e., no numbers are positive) and gives a
complexity of 4+3n.
-
The worst case occurs when U=n (i.e., all
numbers are positive) and gives a complexity of 4+5n.
-
To determine the average case result is much
harder as it requires knowing the input distribution (i.e., are
positive numbers likely) and requires probability theory.
-
We will study primarily worst case complexity.
================ Start Lecture #2 ================
1.1.4 Analyzing Recursive Algorithms
Consider a recursive version of innerProduct. If the arrays are of
size 1, the answer is clearly A[0]B[0]. If n>1, we recursively get
the inner product of the first n-1 terms and then add in the last term.
Algorithm innerProductRecursive
Input: Positive integer n and two integer arrays A and B of size n.
Output: The inner product of the two arrays
if n=1 then
return A[0]B[0]
return innerProductRecursive(n-1,A,B) + A[n-1]B[n-1]
How many steps does the algorithm require? Let T(n) be
the number of steps required.
-
If n=1 we do a comparison, two (array) fetches, a product, and a return.
-
So T(1)=5.
-
If n>1, we do a comparison, a subtraction, a method call, the
recursive computation, two array fetches, a product, a sum and a
return.
-
So T(n) = 1 + 1 + 1 + T(n-1) + 2 + 1 + 1 + 1 = T(n-1)+8.
-
This is called a recurrence equation. In general
these are quite difficult to solve in closed
form, i.e. without T on the right hand side.
-
For this simple recurrence, one can see that T(n)=8n-3 is the
solution.
-
We will learn more about recurrences later.
1.2 Asymptotic Notation
One could easily complain about the specific primitive operations
we chose and about the amount we charge for each one. For example,
perhaps we should charge one unit for accessing a scalar variable.
Perhaps we should charge more for division than for addition. Some
computers can multiply two numbers and add it to a third in one
operation. What about the cost of loading the program?
Now we are going to be less precise and worry only about approximate
answers for large inputs.
Thus the rather arbitrary decisions made about how many units to
charge for each primitive operation will not matter since our
sloppiness (i.e. the approximate forms of our answers) will be valid
for any of these (reasonable) choice of primitive operations and the
charges assigned to each.
Please note that the sloppiness will be very precise.
1.2.1 The Big-Oh
Notation
Definition: Let f(n) and g(n) be real-valued
functions of a single non-negative integer argument.
We write f(n) is O(g(n)) if there is a positive real
number c and a positive integer n0
such that f(n)≤cg(n) for all n≥n0.
What does this mean?
For large inputs (n≥n0), f is not much
bigger than g (specifically, f(n)≤cg(n)).
Examples to do on the board
- 3n-6 is O(n). Some less common ways of
saying the same thing follow.
-
3x-6 is O(x).
-
If f(y)=3y-6 and id(y)=y,
then f(y) is O(id(y)).
-
3n-6 is O(2n)
-
9n4+12n2+1234 is
O(n4).
-
innerProduct is O(n)
-
innerProductBetter is O(n)
-
innerProductFixed is O(n)
-
countPositives is O(n)
-
n+log(n) is O(n).
-
log(n)+5log(log(n)) is O(log(n)).
-
1234554321 is O(1).
-
3/n is O(1). True but not the best.
-
3/n is O(1/n). Much better.
-
innerProduct is
O(3n4+100n+log(n)+34.5).
True, but awful.
A few theorems give us rules that make calculating big-Oh easier.
Theorem (arithmetic): Let d(n),
e(n), f(n), and g(n) be nonnegative
real-valued functions of a nonnegative integer argument and assume
d(n) is O(f(n)) and e(n) is
O(g(n)). Then
-
ad(n) is O(f(n)) for any nonnegative a
-
d(n)+e(n) is O(f(n)+g(n))
-
d(n)e(n) is O(f(n)g(n))
Theorem (transitivity): Let d(n),
f(n), and g(n) be nonnegative real-valued functions
of a nonnegative integer argument and assume d(n) is
O(f(n)) and f(n) is O(g(n)). Then
d(n) is O(g(n)).
Theorem (special functions): (Only n varies)
-
If f(n) is a polynomial of degree d, then
f(n) is O(nd).
-
nk is O(an) for any
k>0 and a>1.
-
log(nk) is O(log(n)) for any k>0
-
(log(n))k is O(nj) for any
k>0 and j>0.
Example: (log n)1000 is
O(n0.001).
This says raising log n to the 1000 is not (significantly) bigger than
the thousandth root of n. Indeed raising log to the 1000 is actually
significantly smaller than taking the thousandth root
since n0.001) is not
O((log n)1000).
So log is a VERY small (i.e., slow growing) function.
Homework: R-1.19 R-1.20
================ Start Lecture #3 ================
Problem Set #1, Problem 1.
The problem set will be officially assigned a little later, but the first
problem in the set is:
Describe in pseudo-code a recursive algorithm
sumAndMax(n, A)
that computes both the sum of the elements of A and the maximum
element.
You may assume n is a positive integer giving the number of
elements in A.
You should return a pair (s,m) where s is the sum and m is the max (in
java this would be an object; in C it would be a struct).
ALSO compute the (worst case) running time for your algorithm.
Give the exact answer AND also Θ notation. So if the
exact answer were 4X7+3X2-2, your answers would
be 4X7+3X2-2 and Θ(X7).
End of Problem Set #1, Problem 1
Example: Let's do problem R-1.10. Consider the
following simple loop that computes the sum of the first n positive
integers and calculate the running time using the big-Oh notation.
Algorithm Loop1(n)
s ← 0
for i←1 to n do
s ← s+i
With big-Oh we don't have to worry about multiplicative or additive
constants so we see right away that the running time is just the
number of iterates of the loop so the answer is O(n)
Homework: R-1.11 and R-1.12
Definitions: (Common names)
-
If a function is O(log(n)), we call it
logarithmic.
-
If a function is O(n),
we call it linear.
-
If a function is O(n2),
we call it quadratic.
-
If a function is O(nk) with k≥1,
we call it polynomial.
-
If a function is O(an) with a>1,
we call it exponential.
Remark: The last definitions would be better with a
relative of big-Oh, namely big-Theta (defined below), since, for
example 3log(n) is O(n2), but we do
not call 3log(n) quadratic.
Homework: R-1.10 and R-1.12.
Example: R-1.13. What is running time of the
following loop using big-Oh notation?
Algorithm Loop4(n)
s ← 0
for i←1 to 2n do
for j←1 to i do
s ← s+1
Clearly the time is determined by the number of executions of the last
statement. But this looks hard since the inner loop is executed a
different number of times for each iteration of the outer loop. But
it is not so bad. For iteration i of the outer loop, the inner loop
has i iterations. So the total number of iterations
of the last statement is 1+2+...+2n, which is 2n(2n+1)/2 (we will
learn this formula soon). So the answer is O(n2).
Homework: R-1.14
1.2.2 Relatives
of the Big-Oh
Big-Omega and Big-Theta
Recall that f(n) is O(g(n)) if, for large n, f is not much bigger
than g. That is g is some sort of upper bound on f.
How about a definition for the case when g is (in the same sense) a
lower bound for f?
Definition: Let f(n) and g(n) be real valued
functions of an integer value. Then f(n) is
Ω(g(n)) if g(n) is O(f(n)).
Remarks:
-
We pronounce f(n) is Ω(g(n)) as "f(n) is big-Omega of g(n)".
-
What the last definition says is that we say f(n) is not much smaller
than g(n) if g(n) is not much bigger than f(n), which sounds
reasonable to me.
-
What if f(n) and g(n) are about equal, i.e., neither is much
bigger than the other?
Definition: We write
f(n) is Θ(g(n)) if both
f(n) is O(g(n)) and f(n) is Ω(g(n)).
Remarks
We pronounce f(n) is Θ(g(n)) as "f(n) is big-Theta of g(n)"
Examples to do on the board.
-
2x2+3x is Θ(x2).
-
2x3+3x is not θ(x2).
-
2x3+3x is Ω(x2).
-
innerProductRecursive is Θ(n).
-
binarySearch is Θ(log(n)). Unofficial for now.
-
If f(n) is Θ(g(n)), then f(n) is &Omega(g(n)).
-
If f(n) is Θ(g(n)), then f(n) is O(g(n)).
Homework: R-1.6
Little-Oh and Little-Omega
Recall that big-Oh captures the idea that for large n, f(n) is not
much bigger than g(n). Now we want to capture the idea that, for
large n, f(n) is tiny compared to g(n).
If you remember limits from calculus, what we want is that
f(n)/g(n)→0 as n→∞.
However, the definition we give does not use the word limit (it
essentially has the definition of a limit built in).
Definition: Let f(n) and g(n) be real valued
functions of an integer variable. We say
f(n) is o(g(n))
if for any c>0,
there is an n0 such that
f(n)≤cg(n) for all n>n0.
This is pronounced as "f(n) is little-oh of g(n)".
Definition: Let f(n) and g(n) be real valued
functions of an integer variable. We say
f(n) is ω(g(n) if
g(n) is o(f(n)). This is pronounced as "f(n) is little-omega of g(n)".
Examples: log(n) is o(n) and x2 is
ω(nlog(n)).
What should we say if f(n) is o(g(n)) and f(n) is ω(g(n))?
Perhaps we should say f(n) is θ(g(n)), i.e., little theta.
NO! Why?
Because we cannot have for large n both f(n)<.5*g(n)
and g(n)<.5*f(n).
Homework: R-1.4. R-1.22
What is "fast" or "efficient"?
If the asymptotic time complexity is bad, say Ω(n8), or
horrendous, say Ω(2n), then for large n, the algorithm will
definitely be slow. Indeed for exponential algorithms even modest n's
(say n=50) are hopeless.
Algorithms that are o(n) (i.e., faster than linear, a.k.a. sub-linear),
e.g. logarithmic algorithms, are very fast and quite rare.
Note that such algorithms do not even inspect most of the input data
once. Binary search has this property. When you look up a name in the
phone book you do not even glance at a majority of the names present.
Linear algorithms (i.e., Θ(n)) are also fast. Indeed, if the
time complexity is O(nlog(n)), we are normally quite happy.
Low degree polynomial (e.g., Θ(n2),
Θ(n3), Θ(n4)) are interesting. They
are certainly not fast but speeding up a computer system by a factor
of 1000 (feasible today with parallelism) means that a
Θ(n3) algorithm can solve a problem 10 times larger.
Many science/engineering problems are in this range.
1.2.3 The Importance of Asymptotics
It really is true that if algorithm A is o(algorithm B) then for
large problems A will take much less time than B.
Definition: If (the number of operations in)
algorithm A is o(algorithm B), we call A
asymptotically faster than B.
Example:: The following sequence of functions are
ordered by growth rate, i.e., each function is
little-oh of the subsequent function.
log(log(n)), log(n), (log(n))2, n1/3,
n1/2, n, nlog(n), n2/(log(n)), n2,
n3, 2n.
What about those constants that we have swept under the rug?
Modest multiplicative constants (as well as immodest additive
constants) don't cause too much trouble. But there are algorithms
(e.g. the AKS logarithmic sorting algorithm) in which the
multiplicative constants are astronomical and hence, despite its
wonderful asymptotic complexity, the algorithm is not used in
practice.
A Great Table
See table 1.10 on page 20.
Homework: R-1.7
================ Start Lecture #4 ================
Homework solutions posted, give passwd
1.3 A Quick Mathematical Review
This is hard to type in using html. The book is fine and I will
write the formulas on the board.
1.3.1 Summations
Definition:
The sigma notation: ∑f(i) with i going from a to b.
Theorem:
Assume 0<a≠1. Then ∑ai i from 0 to n =
(an+1-1)/(a-1).
Proof:
Cute trick. Multiply by a and subtract.
Theorem:
∑i from 1 to n = n(n+1)/2.
Proof:
Pair the 1 with the n, the 2 with the (n-1), etc. This gives a bunch
of (n+1)s. For n even it is clearly n/2 of them. For odd it is the
same (look at it).
1.3.2 Logarithms and Exponents
Recall that logba = c means that bc=a.
b is called the base and c is called the
exponent.
What is meant by log(n) when we don't specify the base?
- Some people use base 10 by default.
- Mathematicians use base e.
- We will use base 2 (common in computer science).
I assume you know what ab is. (Actually this is not so
obvious. Whatever 2 raised to the square root of 3 means it is
not writing 2 down the square root of 3 times and
multiplying.) So you also know that
ax+y=axay.
Theorem:
Let a, b, and c be positive real numbers. To ease writing, I will use
base 2 often. This is not needed. Any base would do.
- log(ac) = log(a)+log(c)
- log(a/c) = log(a) - log(c)
- log(ac) = c log(a)
- logc(a) = (log(a))/log(c):
consider a = clogca and take log of both sides.
- clog(a) = a log(c): take log of both sides.
- (ba)c = bac
- babc = ba+c
- ba/bc = ba-c
Examples
- log(2nlog(n)) = 1 + log(n) + log(log(n)) is Θ(log(n))
- log(log(sqrt(n))) = log(.5log(n)) = log(.5)+log(log(n))
= -1 + log(log(n)) = Θ(log(log(n))
- log(2n) = nlog(2) = n = 2log(n)
Homework: C-1.12
Floor and Ceiling
⌊x⌋ is the greatest integer not greater than x.
⌈x⌉ is the least integer not less than x.
⌊5⌋ = ⌈5⌉ = 5
⌊5.2⌋ = 5 and ⌈5.2⌉ = 6
⌊-5.2⌋ = -6 and ⌈-5.2⌉ = -5
1.3.3 Simple Justification Techniques
By example
To prove the claim that there is a positive n
satisfying nn>n+n, we merely have to note that
33>3+3.
By counterexample
To refute the claim that all positive n
satisfy nn>n+n, we merely have to note that
11<1+1.
By contrapositive
"P implies Q" is the same as "not Q implies not P". So to show
that in the world of positive integers "a2≥b2
implies that a≥b" we can show instead that
"NOT(a≥b) implies NOT(a2≥b2)", i.e., that
"a<b implies a2<b2",
which is clear.
By contradiction
Assume what you want to prove is false and derive
a contradiction.
Theorem:
There are an infinite number of primes.
Proof:
Assume not. Let the primes be p1 up to pk and
consider the number
A=p1p2…pk+1.
A has remainder 1 when divided by any pi so cannot have any
pi as a factor. Factor A into primes. None can be
pi (A may or may not be prime). But we assumed that all
the primes were pi. Contradiction. Hence our assumption
that we could list all the primes was false.
By (complete) induction
The goal is to show the truth of some statement for all integers
n≥1. It is enough to show two things.
- The statement is true for n=1
- IF the statement is true for all k<n,
then it is true for n.
Theorem:
A complete binary tree of height h has 2h-1 nodes.
Proof:
We write NN(h) to mean the number of nodes in a complete binary tree
of height h.
A complete binary tree of height 1 is just a root so NN(1)=1 and
21-1 = 1.
Now we assume NN(k)=2k-1 nodes for all k<h
and consider a complete
binary tree of height h.
It is just two complete binary trees of height
h-1 with new root to connect them.
So NN(h) = 2NN(h-1)+1 = 2(2h-1-1)+1 = 2h-1,
as desired
Homework: R-1.9
Loop Invariants
Very similar to induction. Assume we have a loop with controlling
variable i. For example a "for i←0 to n-1". We then
associate with the loop a statement S(j) depending on j such that
- S(0) is true (just) before the loop begins
- IF S(j-1) holds before iteration j begins,
then S(j) will hold when iteration j ends.
By induction we see that S(n) will be true when the nth iteration
ends, i.e., when the loop ends.
I favor having array and loop indexes
starting at zero. However, here it causes us some grief. We must
remember that iteration j occurs when i=j-1.
Example::
Recall the countPositives algorithm
Algorithm countPositives
Input: Non-negative integer n and an integer array A of size n.
Output: The number of positive elements in A
pos ← 0
for i ← 0 to n-1 do
if A[i] > 0 then
pos ← pos + 1
return pos
Let S(j) be "pos equals the number of positive values in the first
j elements of A".
Just before the loop starts S(0) is true
vacuously. Indeed that is the purpose of the first
statement in the algorithm.
Assume S(j-1) is true before iteration j, then iteration j (i.e.,
i=j-1) checks A[j-1] which is the jth element and updates pos
accordingly. Hence S(j) is true after iteration j finishes.
Hence we conclude that S(n) is true when iteration n concludes,
i.e. when the loop terminates. Thus pos is the correct value to return.
1.3.4 Basic Probability
Skipped for now.
1.4 Case Studies in Algorithm Analysis
1.4.1 A Quadratic-Time Prefix Averages Algorithm
We trivially improved innerProduct (same asymptotic complexity
before and after). Now we will see a real improvement.
For simplicity I do a slightly simpler algorithm than the book does,
namely prefix sums.
Algorithm partialSumsSlow
Input: Positive integer n and a real array A of size n
Output: A real array B of size n with B[i]=A[0]+…+A[i]
for i ← 0 to n-1 do
s ← 0
for j ← 0 to i do
s ← s + A[j]
B[i] ← s
return B
The update of s is performed 1+2+…+n times. Hence the
running time is Ω(1+2+…+n)=&Omega(n2).
In fact it is easy to see that the time is &Theta(n2).
1.4.2 A Linear-Time Prefix Averages Algorithm
Algorithm partialSumsFast
Input: Positive integer n and a real array A of size n
Output: A real array B of size n with B[i]=A[0]+…+A[i]
s ← 0
for i ← 0 to n-1 do
s ← s + A[i]
B[i] ← s
return B
We just have a single loop and each statement inside is O(1), so
the algorithm is O(n) (in fact Θ(n)).
Homework: Write partialSumsFastNoTemps, which is also
Θ(n) time but avoids the use of s (it still uses i so my name is not
great).
================ Start Lecture #5 ================
1.5 Amortization
Often we have a data structure supporting a number of different
operations that will each be applied many times. Sometimes the worst
case time complexity (i.e., the longest amount of time) of a sequence
of n operations is significantly less than n times the worst case
complexity of one operations. We give an example very soon.
If we divide the running time of the sequence by the number of
operations performed we get the average time for each operation in the
sequence, which is called the amortized running
time.
Why amortized?
Because the cost of the occasional expensive application is
amortized over the numerous cheap application (I think).
Example:: (From the book.) The clearable table.
This is essentially an array. The table is initially empty (i.e., has
size zero). We want to support three operations.
-
Add(e): Add a new entry to the table at the end (extending its size).
-
Get(i): Return the ith entry in the table.
-
Clear(): Remove all the entries by setting each entry to zero (for
security) and setting the size to zero.
The natural implementation is to use a large array A and an integer
N indicating the current size of A. More precisely A is (always)
of size B (Big) and N indicates the extent of A that is currently in
use.
Declare A[B] a large integer array, initially all zero
n an integer, initially zero
Algorithm add(e)
A[n] ← e
n ← n+1
Algorithm get(i)
return A[i]
Algorithm clear()
for i ← 0 to n-1
A[i] ← 0
n ← 0
We are ignoring a number of error cases. For example, it is an
error to issue Get(5) if only two entries have been put into the
clearable table.
The question we want to answer is, given an initially empty
clearable table A, what is the worst-case (i.e., largest) time
required for a sequence of K operations (K large).
The amortized cost is this total divided by K.
Add(e) requires an array reference, an addition, and two
assignments for a total cost of 4.
Get(i) requires a reference and a return; cost is 2.
Clear() requires an assignment to i, n+1 tests, n additions to i, n
array references, n assignments to A, and one assignment to n for a
total cost of 4n+3.
So Add is Θ(1), Get is &Theta(1);, and clear is Θ(n).
We start with a size zero table and assume we perform k (legal)
operations. Question: What is the worst-case running time for all k
operations? Once we know the answer, the amortized time is this
answer divided by k. It represents the (worst case) average cost of
each operation.
A difficulty is that we are only given k, the number of operations.
We do not know what is the worst case sequence of operations.
For example, given k=1000, which sequence of 1000 operations is the most
expensive? Since we don't know the sequence we don't know the value
of n when a clear is done.
One upper bound that is easy to compute goes as follows.
Since we execute k operations, n is never bigger than k and hence
clear never costs more than 4k+3. Since get(i) and add(e) cost less
than 4k+3, we see that no single operation can cost more than
4k+3 so k operations cannot cost more than 4k2+3k and the
average cost per operation cannot be more than (4k2+3k)/k
or 4k+3.
Hence the total cost for k operations is O(k2) and the
amortized cost is O(k).
Since we might be overestimating the cost of some operations we
only get big-Oh values not Theta values.
Everything we have said so far is correct; in particular the
amortized cost is O(k). Of course it also is O(k2)
and also O(k50), etc. We naturally prefer the smallest
possible upper bound.
The problem with our analysis so far is that our upper bound is too
big. The amortized cost is actually O(1) (since it is clearly
ω(1), it is also θ(1)).
The reason we have too large an upper bound is that, once we
(correctly) determined that 4k+3 is the most one operation could
cost, we asserted that k(4k+3) is the most k operations could cost.
It is true that if A is the most one operation can cost,
then k operations cannot cost more than kA.
However it is NOT true that if there is one operation that
can cost A, then there is a sequence of k operations that cost as much
as kA.
The point is that you cannot always get a sequence of k operations
such that each one costs as much as the most expensive
operation possible.
Consider the sequence consisting of k-1 add(e)
operations followed by one Clear().
Each add(e) costs 4, for a total of 4k-4.
Since there are k-1 add operations preceding the clear, n=k-1 when the
clear() is invoked.
Hence the clear costs 4(k-1)+3=4k-1 and the total cost of the sequence
is (4k-4)+(4k-1)=8k-5.
So, for this particular sequence, the amortized cost is
(8k-5)/k=8-5/k, which is Θ(1).
But this doesn't look like the most expensive sequence since it has
only one clear and clear is the expensive operation. To be definite
let's assume k=1000. So we know that the sequence of 999 adds
followed by one clear costs a total of 8(1000)-5=7995. Let's try to
make a more expensive sequence.
What if we try two clears, say one in the middle and one at the
end? That is, 499 adds, one clear, 499 adds, one clear. The 998 adds
cost a total of 4(998)=3992. The first clear costs 4(499)+3=1999
(only 499 adds precede the clear so n=499 when the clear is invoked).
Although it is true
that there are 998 adds preceding the second clear, 499 of them have
already been processed by the first clear and n=499 (not 998)
when the second clear is invoked. Thus this clear also costs 1999 and
the entire
sequence costs 3992 for the adds and 2(1999) for the two clears, for a
grand total of 7990. This is less than the cost of our first
sequence.
But maybe the problem is that we should have put both clears at the
end where they are the most expensive, i.e. 998 adds, clear, clear.
The 998 adds still cost 3992. The first clear is expensive, but now
the second one is very cheap since n=0!
In fact no matter what sequence of k operations you construct the
total number of adds cannot exceed k and thus and this means that all
the clears combined can clear no more than k values.
Since the cost of a clear is 4n+3 when n items are present, we see
that the total of all the n's in all the clears cannot exceed
k. Hence all the clears combined have complexity O(k) (since we found
a sequence, the first one considered, where the clear costs 4k+2, the
complexity is θ(k)).
Hence, the amortized time for each operation in the clearable table
ADT (abstract data type) is O(1), in fact Θ(1). That is, the
worst case total time for k operations is Θ(k).
Why?
-
All the clears have complexity O(k) in total (shown above).
-
All the Adds have complexity O(k) in total: There are O(k) Adds in
the sequence and each one has Θ(1) complexity.
-
Similarly all the Gets have complexity O(k) in total.
-
Hence the total complexity is O(k)+O(k)+O(k), which is O(k).
-
But there are a total of k operations each with complexity
Ω(1), so the total has complexity Ω(k).
-
So we have show the total complexity of any sequence of k
operations is O(k) and is Ω(k).
-
Hence the total complexity
of the sequence is Θ(k) and the amortized
complexity is Θ(k)/k, which is &Theta(1);.
Note that we first found an upper bound on the complexity (i.e.,
big-Oh) and then a lower bound (Ω). Together this gave Θ.
1.5.1 Amortization Techniques
The Accounting Method
Overcharge for cheap operations and undercharge expensive so that
the excess charged for the cheap (the profit) covers the undercharge
(the loss). This is called in accounting an amortization schedule.
Assume the get(i) and add(e) really cost one ``cyber-dollar'',
i.e., there is a constant B so that they each take fewer than B
primitive operations and we let a ``cyber-dollar'' be B. Similarly,
assume that clear() costs P cyber-dollars when the table has P
elements in it.
We charge 2 cyber-dollars for every operation. So we have a profit
of 1 cyber-dollar on each add(e) and we see that the profit is enough
to cover next clear() since if we clear P entries, we had P add(e)s.
All operations cost 2 cyber-dollars so k operations cost 2k. Since
we have just seen that the real cost is no more than the cyber-dollars
spent, the total cost is O(k) and the amortized cost is
O(1). Since every operation has cost Ω(1), the amortized cost
is Θ(1).
Potential Functions
Very similar to the accounting method. Instead of banking money,
you increase the potential energy. I don't believe we will use this
method so we are skipping it. If you like physics more than
accounting, you might prefer it.
1.5.2 Analyzing an Extendable Array Implementation
We want to let the size of an array grow dynamically (i.e., during
execution).
The implementation is quite simple. Copy the old array into a new one
twice the size. Specifically, on an array overflow instead of
signaling an error perform the following steps (assume the array is A
and the current size is N)
- Allocate a new array B of size 2N
- For i←0 to N-1 do B[i]←A[i]
- Make A refer to B (this is A=B in java).
- Deallocate the old A (automatic in java; error prone in C)
The cost of this growing operation is Θ(N).
Theorem:
Given an extendable array A that is initially empty and of size N, the
amortized time to perform n add(e) operations is Θ(1).
Proof:
Assume one cyber dollar is enough for an add w/o the grow and that N
cyber-dollars are enough to grow from N to 2N.
Charge 2 cyber dollars for each add; so a profit of 1 for each add w/o
growing.
When you must do a grow, you had N adds so have N dollars banked.
Hence the amortized cost is O(1). Since Omega;(1) is obvious, we get
Θ(1).
Alternate Proof that the amortized time is
O(1). Note that amortized time is O(1) means that the total time is O(N).
The new proof is a two step procedure
-
The total memory used is bounded by a constant times N.
-
The time per memory cell is bounded by a constant.
Hence the total time is bounded by a constant times the number of
memory cells and hence is bounded by a constant times N.
For step one we note that when the N add operations are complete
the size of the array will be FS<.2N, with FS a power of 2. Let
FS=2k So the total size used is
TS=1+2+4+8+...+FS=∑2i (i from 0 to k). We
already proved that this is
(2k+1-1)/(2-1)=2k+1-1=2FS-1<4N as desired.
An easier way to see that the sum is 2k+1-1 is to write
1+2+4+8+...2k in binary, in which case we get (for k=5)
1
10
100
1000
10000
+100000
------
111111 = 1000000-1 = 25+1-1
The second part is clear. For each cell the algorithm only does a
bounded number of operations. The cell is allocated, a value is
copied in to the cell, and a value is copied out of the cell (and into
another cell).
================ Start Lecture #6 ================
Note from Nelya
The CAS Learning Center is offering tutoring services
for students needing help in 002, 004, 201, or 310.
You can announce this in your classes. The website for
the CAS Learning Center is http://www.nyu.edu/cas/clc/.
The schedule is listed on the site.
End of Note
1.6 Experimentation
1.6.1 Experimental Setup
The book is quite clear. I have little to add.
Choosing the question
You might want to know
- Average running time.
- Compare two algorithms for speed.
- Determine the running time dependence of parameters of the
algorithm.
- For algorithms that generate approximations, test how close they
come to the correct value.
Deciding what to measure
- Memory references (increasingly important--unofficial hardware
comment).
- Comparisons (for sorting, searching, etc).
- Arithmetic ops (for numerical problems).
1.6.2 Data Analysis and Visualization
Ratio test
Assume you believe the running time t(n) of an algorithm is
Θ(nd) for some specific d and you want to both
verify your assumption and find the multiplicative constant.
Make a plot of (n, t(n)/nd). If you are right the
points should tend toward a horizontal line and the height of this
line is the multiplicative constant.
Homework: R-1.29
What if you believe it is polynomial but don't have a guess for d?
Ans: Use ...
The power test
Plot (n, t(n)) on log log paper. If t(n) is
Θ(nd), say t(n) approaches bnd, then
log(t(n)) approaches log(b)+d(log(n)).
So when you plot (log(n), log(t(n)) (i.e., when you use log log
paper), you will see the points approach (for large n) a straight line
whose slope is the exponent d and whose y intercept is the
multiplicative constant b.
Homework: R-1.30
Chapter 2 Basic Data Structures
2.1 Stacks and Queues
2.1.1 Stacks
Stacks implement a LIFO (last in first out)
policy. All the action occurs at the top of the
stack, primarily with the push(e) and
pop operation.
The stack ADT supports
-
push(e): Insert e at TOS (top of stack).
-
pop(): Remove and return TOS. Signal error if the stack empty.
-
top(): Return TOS. Signal an error if empty.
-
size(): Return the current numbers of elements in the stack.
-
isEmpty(): Shortcut for the boolean expression size()=0.
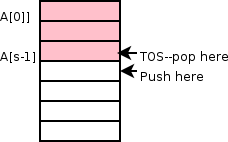
There is a simple implementation using an array A and an integer s
(the current size). A[s-1] contains the TOS.
Objection (your honor).
The ADT says we can always push.
A simple array implementation would need to signal an error if the
stack is full.
Sustained! What do you propose instead?
An extendable array.
Good idea.
Homework: Assume a software system has 100 stacks
and 100,000 elements that can be on any stack. You do not know how
the elements are to be distributed on the stacks. However, once an
element is put on one stack, it never moves. If you used a normal
array based implementation for the stacks, how much memory will you
need. What if you use an extendable array based implementation?
Now answer the same question, but assume you have Θ(S) stacks and
Θ(E) elements.
Applications for procedure calls (unofficial)
Stacks work great for implementing procedure calls since procedures
have stack based semantics. That is, last called is first returned and
local variables allocated with a procedure are deallocated when the
procedure returns.
So have a stack of "activation records" in which you keep the
return address and the local variables.
Support for recursive procedures comes for free. For languages
with static memory allocations (e.g., fortran) one can store the local
variables with the method. Fortran forbids recursion so that memory
allocation can be static. Recursion adds considerably flexibility to
a language as some cost in efficiency.
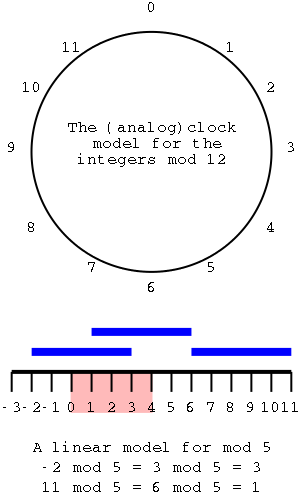
A Review of (the Real) Mod
I am reviewing modulo since I believe it is no longer taught in
high school.
The top diagram shows an almost ordinary analog clock. The major
difference is that instead of 12 we have 0. The hands would be useful
if this was a video, but I omitted them for the static picture.
Positive numbers go clockwise (cw) and negative counter-clockwise
(ccw). The numbers shown are the values mod 12. This example is good
to show arithmetic. (2-5) mod 12 is obtained by starting at 2 and
moving 5 hours ccw, which gives 9. (-7) mod 12 is (0-7) mod 12 is
obtained by starting at 0 and going 7 hours ccw, which gives 5.
To get mod 8, divide the circle into 8 hours
instead of 12.
The bottom picture shows mod 5 in a linear fashion. In pink are
the 5 values one can get when doing mod 5, namely 0, 1, 2, 3, and 4.
I only illustrate numbers from -3 to 11 but that is just due to space
limitations. Each blue bar is 5 units long so the numbers at its
endpoints are equal mod 5 (since they differ by 5). So you just lay
off the blue bar until you wind up in the pink.
End of Mod Review
Personal rant:
I object to programming languages using
the well known and widely used function name mod and changing its
meaning. My math training prevents me from accepting that mod(-3,10)
is -3. The correct value is 7.
The book, following java, defines mod(x,y) as
x-⌊x/y⌋y.
This is not mod but remainder.
Think of x as the dividend, y as the divisor and then
⌊x/y⌋ is the quotient. We remember from elementary school
dividend = quotient * divisor + remainder
remainder = dividend - quotient * divisor
The last line is exactly the book's and java's definition of mod.
My favorite high level language, ada, gets it right in the
obvious way: Ada defines both mod and remainder
(ada extends the math definition of mod to the case where the second
argument is negative).
In the familiar case when x≥0 and y>0 mod and remainder are
equal. Unfortunately the book uses mod sometimes when x<0 and
consequently needs to occasionally add an extra y to get the true mod.
End of personal rant
Homework: Using the real mod (let's call it
RealMod) evaluate
-
RealMod(8,3)
-
RealMod(-8,3)
-
RealMod(10000007,10)
-
RealMod(-10000007,10)
Implementing (Real) Mod
Unlike past years, I will use the real mod this year (and call it
simply mod). The only disadvantage is that the real mod isn't a java
primitive. Although I am confident it must be in some java library, I
like programming more than searching library listings when the desired
method is so simple. So I actually implemented two versions of mod in
java. The first one is based on the definition of mod(a,b) as the
number n such that 0≤n<b and |n-a| is a multiple of b (the
latter condition is normally stated “n is congruent to a modulo
b)”. This implementation uses only addition and subtraction.
The second implementation, which is only one line long, uses the java
%. However, it is quite ugly.
The java code is here. Please note
that almost all of it is scaffolding to generate tests and print
results. The implementations of mod are at the end.
A run of the tests is here.
2.1.2 Queues
Queues implement a FIFO (first in first out) policy. Elements are
inserted at the rear and removed from the
front using the enqueue and
dequeue operations respectively.
The queue ADT supports
-
enqueue(e): Insert e at the rear.
-
dequeue(): Remove and return the front element. Signal an error if
the queue is empty.
-
front(): Return the front element. Signal an error if empty.
-
size(): Return the number of elements currently present.
-
isEmpty(): Abbreviation for size()=0
Simple array implementation
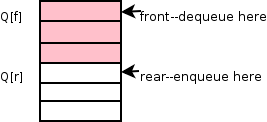 For queues we need a
front and rear "pointers" f and r. Since we are using arrays f and r
are actually indexes not pointers. Calling the array Q, Q[f] is the
front element of the queue, i.e., the element that would be returned
by dequeue(). Similarly, Q[r] is the element into which enqueue(e)
would place e. There is one exception: if f=r, the queue is empty so
Q[f] is not the front element.
For queues we need a
front and rear "pointers" f and r. Since we are using arrays f and r
are actually indexes not pointers. Calling the array Q, Q[f] is the
front element of the queue, i.e., the element that would be returned
by dequeue(). Similarly, Q[r] is the element into which enqueue(e)
would place e. There is one exception: if f=r, the queue is empty so
Q[f] is not the front element.
Without writing the code, we see that f will be increased by each
dequeue and r will be increased by every enqueue.
Assume Q has n slots Q[0]…Q[N-1] and the queue is initially
empty with f=r=0. Now consider enqueue(1); dequeue(); enqueue(2);
dequeue(); enqueue(3); dequeue(); …. There is never more than
one element in the queue, but f and r keep growing so after N
enqueue(e);dequeue() pairs, we cannot issue another operation.
Simple circular-array implementation
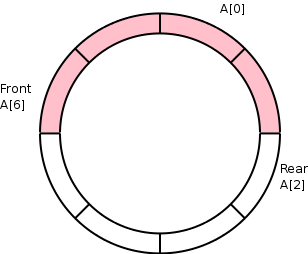 The solution to this problem is to treat the array as circular,
i.e., right after Q[N-1] we find Q[0]. The way to implement this is
to arrange that when either f or r is N-1, adding 1 gives 0 not N.
Similarly for r. So the increment statements become
The solution to this problem is to treat the array as circular,
i.e., right after Q[N-1] we find Q[0]. The way to implement this is
to arrange that when either f or r is N-1, adding 1 gives 0 not N.
Similarly for r. So the increment statements become
f←(f+1) mod N
r←(r+1) mod N
Note: Recall that we had some grief due to our
starting arrays and loops at 0. For example, the fifth slot of A is
A[4] and the fifth iteration of "for i←0 to 30" occurs when i=4.
The updates of f and r directly above show one of the advantages of
starting at 0; they are less pretty if the array starts at 1.
The size() of the queue seems to be r-f, but this is not always
correct since the array is circular.
For example let N=10 and consider an initially empty queue with f=r=0 that has
enqueue(10)enqueue(20);dequeue();enqueue(30);dequeue();enqueue(40);dequeue()
applied. The queue has one element, r=4, and f=3, so r-f=1 as expected.
But now apply 6 more enqueue(e) operations
enqueue(50);enqueue(60);enqueue(70);enqueue(80);enqueue(90);enqueue(100)
At this point the array has 7 elements, r=0, and f=3.
Clearly the size() of the queue is not r-f=-3.
It is instead 7, the number of elements in the queue.
The problem is that r in some sense is 10 not 0 since there were 10
enqueue(e) operations. In fact if we kept 2 values for f and 2 for r,
namely the value before the mod and after, then size() would be
rBeforeMod-fBeforeMod. Instead we, use the following formula.
size() = (r-f) mod N
Remark: If we used java's definition of mod so
that -3 mod 10 gave -3, we would need the inelegant formula
size() = (r-f+N) mod N.
Since isEmpty() is simply an abbreviation for the test size()=0, it
is just testing if r=f.
Algorithm front():
if isEmpty() then
signal an error // throw QueueEmptyException
return Q[f]
Algorithm dequeue():
if isEmpty() then
signal an error // throw QueueEmptyException
temp←Q[f]
Q[f]←NULL // for security or debugging
f←(f+1) mod N
return temp
Algorithm enqueue(e):
if size() = N-1 then
signal an error // throw QueueFullException
Q[r]←e
r←(r+1) mod N
Examples in OS (unofficial)
Round Robin processor scheduling is queue based as is fifo disk
arm scheduling.
More general processor or disk arm scheduling policies often use
priority queues (with various definitions of priority). We will learn
how to implement priority queues later this chapter (section 2.4).
Homework (unofficial): (You may refer to your 202
notes if you wish; mine are on-line based on my home page). How can
you interpret Round Robin processor scheduling and fifo disk
scheduling as priority queues. That is what is the priority? Same
question for SJF (shortest job first) and SSTF (shortest seek time
first). If you have not taken an OS course (202 or equivalent at some
other school), you are exempt from this question. Just write on you
homework paper that you have not taken an OS course.
Problem Set #1, Problem 2:
Please read this question carefully; it is similar to but
different from the one in class.
You are given an Abstract Data Type (ADT) for some kind of container
that includes an insert(x) method and a clean() method.
Insert(x) adds an item to the container; clean() removes all items.
The complexity of insert(x) is k, the number of items in the container
after the insert has completed.
The complexity of clean() is k3, where k is the number of
items in the container
before the clean is executed.
Assume the container is initially empty and that you are to perform a
total of N operations, each an insert(x) or a clean() (all the
x's are distinct).
-
Which sequence of N operations costs the most?
-
What is the amortized cost of the sequence you gave?
-
Rewrite the answer using Θ notation in simplest terms.
End of Problem 2
================ Start Lecture #7 ================
Note: See the java implementation of mod in lecture 6.
Problem Set #1, problem 3: C-2.3
2.2 Vectors, Lists, and Sequences
Unlike stacks and queues, the structures in this section support
operations in the middle, not just at one or both ends.
2.2.1 Vectors
The rank of an element in a sequence is the number
of elements before it. So if the sequence contains n elements,
0≤rank<n.
A vector storing n elements supports:
-
elemAtRank(r): Return the element with rank r. Report an error
if r<0 or r>n-1.
-
replaceAtRank(r,e): Replace the element at rank r with e and
return it. Report an error if r<0 or r>n-1.
-
insertAtRank(r,e): Insert e at rank r moving up existing
elements with rank r and above. Report an error if r<0 or
r>n. If r=n, then we are inserting at the end (i.e., after all
existing elements), which is not an error.
-
removeAtRank(r): Remove the element at rank r moving down existing
elements with rank exceeding r. Report an error if r<0 or
r>n-1.
-
size().
-
isEmpty().
A Simple Array-Based Implementation
Use an array A and store the element with rank r in A[r].
-
Must shift elements when doing an insert or delete, which is
expensive.
-
The code is below does not include the error checks in the ADT
-
We limit the number of elements to N, the declared size of the
array.
-
How can we remove the above limitation?
Ans: Use an extendable array.
Algorithm insertAtRank(r,e)
for i = n-1, n-2, ..., r do
A[i+1]←A[i]
A[r]←e
n←n+1
Algorithm removeAtRank(r)
e←A[r]
for i = r, r+1, ..., n-2 do
A[i]←A[i+1]
n←n-1
return e
The worst-case time complexity of these two algorithms is
Θ(n); the remaining algorithms are all Θ(1).
Homework: When does the worst case occur for
insertAtRank(r,e) and removeAtRank(r)?
By using a circular array we can achieve Θ(1) time for
insertAtRank(0,e) and removeAtRank(0). Indeed, that is the fourth
problem of the first problem set.
Problem Set #1, Problem 4:
Part 1: C-2.5 from the book
Part 2: This implementation still has worst case complexity
Θ(n). When does the worst case occur?
Problem Set #1 is complete: it is due in 3
lectures (7 October).
2.2.2 Lists
So far we have been considering what Knuth refers to as sequential
allocation, when the next element is stored in the next location.
Now we will be considering linked allocation, where each element
refers explicitly to the next and/or preceding element(s).
Positions and Nodes
We think of each element as contained in a node,
which is a container that also contains references to the preceding
and/or following node.
-
In C: struct node { int element; struct node *next; struct node *prev;}
-
In java: class Node { int element; Node next; Node prev;}
But we don't want to expose Nodes to user's algorithms
since this would freeze the possible implementation.
Instead we define the idea (i.e., ADT) of a
position in a list.
The only method available to users is
-
element(): Return the element stored in this position.
The List ADT
Given the position ADT, we can now define the methods for the list
ADT. The first methods only query a list; the last ones actually
modify it.
-
-------------------------- read-only ------------------------
-
first(): Return the position of the first element; error if L is
empty.
-
last(): Return the position of the last element; error if empty.
-
isFirst(p): Abbreviates p=first().
-
isLast(p): Abbreviates p=last().
-
before(p): Return the position preceding p; error if isFirst(p).
-
after(p): Return the position following p; error if isLast(p).
-
size():
-
isEmpty():
-
-------------------------- updates ------------------------
-
replaceElement(p,e): Store e at p, return replaced element.
-
swapElements(p,q): Swap the elements at p and q.
-
insertBefore(p,e): Insert e in the position before p. The book
says it is an error if p is the first position; that seems wrong,
especially considering the next method. I explain what they
likely meant below
-
insertFirst(e): Abbreviates insertBefore(first(),e).
-
insertAfter(p,e): Insert e in the position after p (analogous
error comment).
-
insertLast(e): Abbreviates insertAfter(last(),e).
-
remove(p): Remove the element at position p.
A Linked List Implementation
Now when we are implementing a list we can certainly use
the concept of nodes.
In a singly linked list each node contains a next
link that references the next node.
A doubly linked list contains, in addition prev link
that references the previous node.
Singly linked lists work well for stacks and queues, but do not
perform well for general lists. Hence we use doubly linked lists
Homework: What is the worst case time complexity
of insertBefore for a singly linked list implementation and when does
it occur?
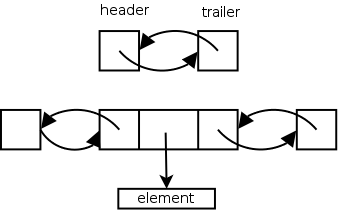
It is convenient to add two special nodes, a
header and trailer. The header has
just a next component, which links to the first node and the trailer
has just a prev component, which links to the last node. For an empty
list, the header and trailer link to each other and for a list of size
1, they both link to the only normal node.
In order to proceed from the top (empty) list to the bottom list
(with one element), one would need to execute one of the insert
methods. Ignoring the abbreviations, this means either
insertBefore(p,e) or inserAfter(p,e). But this means that header
and/or trailer must be an example of a position, one for which there
is no element.
This observation explains the authors' comment above
that insertBefore(p,e) cannot be applied if p is the first position.
What they mean is that when we permit header and trailer to be
positions, then we cannot insertBefore the first position, since that
position is the header and the header has no prev. Similarly we
cannot insertAfter the final position since that position is the
trailer and the trailer has no next.
Clearly not the authors' finest hour.
A list object contains three components, the header, the trailer,
and the size of the list. Note that the book forgets to update the
size for inserts and deletes.
Implementation Comment I have not done the
implementation. It is probably easiest to have header and trailer
have the same three components as a normal node, but have the prev of
header and the next of trailer be some special value (say NULL) that
can be tested for.
The insertAfter(p,e) Algorithm
The position p can be header, but cannot be trailer.
Algorithm insertAfter(p,e):
If p is trailer then signal an error
size←size+1 // missing in book
Create a new node v
v.element←e
v.prev←p
v.next←p.next
(p.next).prev←v
p.next← v
return v
Do on the board the pointer updates for two cases: Adding a node
after an ordinary node and after header. Note that they are the
same. Indeed, that is what makes having the header and trailer so
convenient.
Homework: Write pseudo code for insertBefore(p,e).
Note that insertAfter(header,e) and insertBefore(trailer,e) appear
to be the only way to insert an element into an empty list. In
particular, insertFirst(e) fails for an empty list since it performs
insertBefore(first()) and first() generates an error for an empty list.
The remove(p) Algorithm
We cannot remove the header or trailer. Notice that removing the
only element of a one-element list correctly produces an empty list.
Algorithm remove(p):
if p is either header or trailer signal an error
size←size-1 // missing in book
t←p.element
(p.prev).next←p.next
(p.next).prev←p.prev
p.prev←NULL // for security or debugging
p.next←NULL
return t
================ Start Lecture #8 ================
| Operation | Array | List
|
|---|
| size, isEmpty | O(1) | O(1)
|
| atRank, rankOf, elemAtRank | O(1) | O(n)
|
| first, last, before, after | O(1) | O(1)
|
| replaceElement, swapElements | O(1) | O(1)
|
| replaceAtRank | O(1) | O(n)
|
| insertAtRank, removeAtRank | O(n) | O(n)
|
| insertFirst, insertLast | O(1) | O(1)
|
| insertAfter, insertBefore | O(n) | O(1)
|
| remove | O(n) | O(1)
Asymptotic complexity of the methods for both the array and
list based implementations
|
2.2.3 Sequences
Define a sequence ADT that includes all the methods of both vector
and list ADTs as well as
- atRank(r): Return the position of the element at rank r.
- rankOf(p): Return the rank of the element at position p.
Sequences can be implemented as either circular arrays, as we did
for vectors, or doubly linked lists, as we did for lists. Neither
clearly dominates the other. Instead it depends on the relative
frequency of the various operations. Circular arrays are faster for
some and doubly liked lists are faster for others as the table to the
right illustrates.
Iterators
An ADT for looping through a sequence one element at a time. It
has two methods.
- hasNext: Test whether there are elements left in the iterator
- nextObject: Return and remove the next object in the iterator
When you create the iterator it has all the elements of the
sequence. So a typical usage pattern would be
create iterator I for sequence S
while I.hasNext
process I.nextObject
2.3 Trees
The tree ADT stores elements hierarchically.
There is a distinguished root node. All other nodes
have a parent of which they are a
child. We use nodes and positions interchangeably
for trees.
The definition above precludes an empty tree. This is a matter of
taste some authors permit empty trees, others do not.
Some more definitions.
-
Nodes with the same parent are called siblings.
-
A node without children is called external by the
authors. Also common is to call such nodes
leaves.
-
A node with children is called internal.
-
An ancestor of a node is either the node itself
or an ancestor of the parent of the node. This says that the
ancestors include the node, the node's parent, the parent's
parent, ... up to the root.
-
A node v is a descendent of a node u if u is an
ancestor of v.
-
The subtree rooted at v is the tree consisting of
all the descendents of v.
-
A tree is ordered if there is a linear ordering
of the children of each node. That is, there is a first child, a
second child, etc.
-
A binary tree is one in which all nodes have
at most two children.
-
A proper binary tree is one
in which no node has exactly one child. This means that all
internal nodes have two children.
-
In a binary tree we label each child as either a left
child or as a right child.
-
The subtree routed at the left child of v is called the
left subtree of v.
-
Similarly we define the right subtree of v.
-
The depth of a node is the number of ancestors
not including the node itself.
-
The height of a node is the length of a longest
path to a leaf.
-
The height of a tree is the height of the root.
We order the children of a binary tree so that the left child comes
before the right child.
There are many examples of trees. You learned or will learn
tree-structured file systems in 202. However, despite what the book
says, for Unix/Linux at least, the file system does not form a
tree (due to hard and symbolic links).
These notes can be thought of as a tree with nodes corresponding to
the chapters, sections, subsections, etc.
Games like chess are analyzed in terms of trees. The root is the
current position. For each node its children are the positions
resulting from the possible moves. Chess playing programs often limit
the depth so that the number of examined moves is not too large.
An arithmetic expression tree
The leaves are constants or variables and the internal nodes are binary
arithmetic operations (+,-,*,/).
The tree is a proper ordered binary tree (since we are considering
binary operators).
The value of a leaf is the value of the constant or variable.
The value of an internal node is obtained by applying the operator to
the values of the children (in order).
Evaluate an arithmetic expression tree on the board.
Homework: R-2.2, but made easier by replacing 21
by 10. If you wish you can do the problem in the book instead (I
think it is harder).
2.3.1 The Tree Abstract Data Type
We have three accessor methods (i.e., methods that
permit us to access the nodes of the tree.
- root(): Return the root of the tree.
- parent(v): Return the parent of the node v. Error if v is
the root.
- children(v): Return an iterator of the children of v (in order if
the tree is ordered).
We have four query methods that test status.
- isInternal(v): Tests if v is internal.
- isLeaf(v): Tests if v is a leaf.
- isExternal(v): Same as isLeaf(v).
- isRoot(v): Tests if v is the root.
Finally generic methods that are useful but not
related to the tree structure.
- size(): Return the number of nodes
- elements(): Return an iterator of all the elements stored
in nodes (in no particular order).
- positions: Return an iterator of all the nodes of the tree.
- swapElements(v,w): Swap the elements in nodes v and w.
- replaceElement(v,e): Replace with e and return the element stored
at v.
================ Start Lecture #9 ================
2.3.2 Tree Traversal
Traversing a tree is a systematic method for
accessing or "visiting" each node. We will see and analyze three tree
traversal algorithms, inorder, preorder, and postorder. They differ in
when we visit an internal node relative to its children. In
preorder we visit the node first, in postorder we visit it last, and
in inorder, which is only defined for binary trees, we visit the node
between visiting the left and right children.
Recursion will be a very big deal in traversing
trees!!
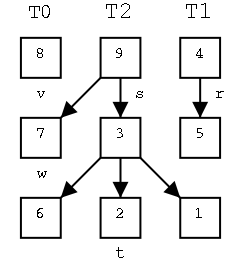
Motivating the Recursive Routines
On the right are three trees. The left one just has a root, the
right has a root with one leaf as a child, and the middle one has
six nodes. For each node, the element in that node is shown inside
the box. All three roots are labeled and 2 other nodes are
also labeled. That is, we give a name to the position, e.g. the left
most root is position v. We write the name of the position under the
box.
We call the left tree T0 to remind us it has height zero. Similarly
the other two are labeled T2 and T1 respectively.
Our goal in this motivation is to calculate the sum the elements in
all the nodes of each tree. The answers are, from left to right, 8,
28, and 9.
For a start, lets write an algorithm called treeSum0
that calculates the sum for
trees of height zero. In fact the algorithm, will contain two
parameters, the tree and a node (position) in that tree, and our
algorithm will calculate the sum in the subtree rooted at the given
position assuming the position is at height 0. Note this is trivial:
since the node has height zero, it has no children and the sum desired
is simply the element in this node. So legal invocations would
include treeSum0(T0,s) and treeSum0(T2,t). Illegal invocations would
include treeSum0(T0,t) and treeSum0(T1,r).
Algorithm treeSum0(T,v)
Inputs: T a tree; v a height 0 node of T
Output: The sum of the elements of the subtree routed at v
Sum←v.element()
return Sum
Now lets write treeSum1(T,v), which calculates the sum for a node
at height 1. It will use treeSum0 to calculate the sum for each
child.
Algorithm treeSum1(T,v)
Inputs: T a tree; v a height 1 node of T
Output: the sum of the elements of the subtree routed at v
Sum←v.element()
for each child c of v
Sum←Sum+treeSum0(T,c)
return Sum
OK. How about height 2?
Algorithm treeSum2(T,v)
Inputs: T a tree; v a height 2 node of T
Output: the sum of the elements of the subtree routed at v
Sum←v.element()
for each child c of v
Sum←Sum+treeSum1(T,c)
return Sum
So all we have to do is to write treeSum3, treSum4, ... , where
treSum3 invokes treeSum2, treeSum4 invokes treeSum3, ... .
That would be, literally, an infinite amount of work.
Do a diff of treeSum1 and treeSum2.
What do you find are the differences?
In the Algorithm line and in the first comment a 1 becomes a 2.
In the subroutine call a 0 becomes a 1.
Why can't we write treeSumI and let I vary?
Because it is illegal to have a varying name for an algorithm.
The solution is to make the I a parameter and write
Algorithm treeSum(i,T,v)
Inputs: i≥0; T a tree; v a height i node of T
Output: the sum of the elements of the subtree routed at v
Sum←v.element()
for each child c of v
Sum←Sum+treeSum(i-1,T,c)
return Sum
This is wrong, why?
Because treeSum(0,T,v) invokes treeSum(-1,c,v), which doesn't
exist because i<0
But treeSum(0,T,v) doesn't have to call anything since v can't have
any children (the height of v is 0). So we get
Algorithm treeSum(i,T,v)
Inputs: i≥0; T a tree; v a height i node of T
Output: the sum of the elements of the subtree routed at v
Sum←v.element()
if i>0 then
for each child c of v
Sum←Sum+treeSum(i-1,T,c)
return Sum
The last two algorithms are recursive; they call themselves.
Note that when treeSum(3,T,v) calls treeSum(2,T,c), the new treeSum
has new variables Sum and c.
We are pretty happy with our treeSum routine, but ...
The algorithm is wrong! Why?
The children of a height i node need not all be of height i-1.
For example s is hight 2, but its left child w is height 0.
(A corresponding error also existed in treeSum2(T,v)
But the only real use we are making of i is to prevent us from
recursing when we are at a leaf (the i>0 test).
But we can use isInternal instead, giving our final algorithm
Algorithm treeSum(T,v)
Inputs: T a tree; v a node of T
Output: the sum of the elements of the subtree routed at v
Sum←v.element()
if T.isInternal(v) then
for each child c of v
Sum←Sum+treeSum(T,c)
return Sum
Our medium term goal is to learn about tree traversals (how to
"visit" each node of a tree once) and to analyze their complexity.
Complexity of Primitive Operations
Our complexity analysis will proceed in a somewhat unusual order.
Instead of starting with the bottom or lowest level routines (the tree
methods in 2.3.1, e.g., is Internal(v)) or the top level routines (the
traversals themselves),
we will begin by analyzing some middle level procedures assuming the
complexities of the low level are as we assert them to be. Then we
will analyze the traversals using the middle level routines and
finally we will give data structures for trees that achieve our
assumed complexity for the low level.
Let's begin!
Complexity Assumptions for the Tree ADT
These assumptions will be verified later.
- root(), parent(v), isInternal(v), isLeaf(v), isRoot(v),
swapElements(v,w), replaceElement(v,e) each take Θ(1) time.
- The methods returning iterators, namely children(v), elements(),
and positions(), each take time Θ(k), where k is the number of
items being iterated over. k=#children for the first method and
#nodes for the other two.
- For each iterator, the methods hasNext() and nextObject() take
Θ(1) time. nextObject() sometimes has other names like
nextPosition() or nextNode() or nextChild().
Middle level routines depth and height
Definitions of depth and
height.
- The depth of the root is 0.
- The height of a leaf is 0.
- The depth of a non-root v is 1 plus the depth of parent(v).
- The height of an internal node v is 1 plus the maximum
height of the children of v.
- The height of a tree is the height of its root.
Remark: Even our definitions are recursive!
From the recursive definition of depth, the recursive algorithm for
its computation essentially writes itself.
Algorithm depth(T,v)
if T.isRoot(v) then
return 0
else
return 1 + depth(T,T.parent(v))
The complexity is Θ(the answer), i.e. Θ(dv),
where dv is the depth of v in the tree T.
The following algorithm computes the height of a position in a tree.
Algorithm height(T,v):
if T.isLeaf(v) then
return 0
else
h←0
for each w in T.children(v) do
h←max(h,height(T,w))
return h+1
Remarks on the above algorithm
-
The loop could (perhaps should) be written in pure iterator style.
Note that T.children(v) is an iterator.
-
This algorithm is not so easy to convert to non-recursive form
Why?
It is not tail-recursive, i.e. the recursive invocation is not
just at the end.
-
To get the height of the tree, execute height(T,T.root())
Algorithm height(T)
height(T,T.root())
Let's use the "official" iterator style.
Algorithm height(T,v):
if T.isLeaf then
return 0
else
h←0
childrenOfV←T.children(v) // "official" iterator style
while childrenOfV.hasNext()
h&lar;max(h,height(T,childrenOfV.nextObject())
return h+1
But the children iterator is defined to return the empty set for a
leaf so we don't need the special case
Algorithm height(T,v):
h←0
childrenOfV←T.children(v) // "official" iterator style
while childrenOfV.hasNext()
h←max(h,height(T,childrenOfV.nextObject())
return h+1
Theorem: Let T be a tree with n nodes and let
cv be the number of children of node v. The sum of
cv over all nodes of the tree is n-1.
Proof:
This is trivial! ... once you figure out what it is saying.
The sum gives the total number of children in a tree. But this almost
all nodes. Indeed, there is just one exception.
What is the exception?
The root.
Corollary: Computing the height of an n-node tree
has time complexity Θ(n).
Proof:
Look at the code of the first version.
-
Since each node calls height on each of its children, height is
called recursively for every node that is a child, i.e. all but
the root. The root is called directly from the top level.
-
Hence height(T,v) is called once for each node v.
-
"Most" of the code in height is clearly Θ(1) per call, or
Θ(n) in total. The exception is the loop.
-
Each iteration of the loop is Θ(1).
-
The number of iterations in the invocation height(T,v) is the
number of children in v.
-
Hence the total number of iterations is the total number of
children, which by the theorem is n-1.
-
Hence the total cost of all the iterations is Θ(n).
-
Hence the total cost of height(T) is the cost of "most" of the
code plus the cost of the loops, which is Θ(N)+Θ(N),
i.e. Θ(N).
To be more formal, we should look at the "official" iterator
version. The only real difference is that in the official version, we
are charged for creating the iterator. But the charge is the number
of elements in the iterator, i.e., the number of children this node
has. So the sum of all the charges for creating iterators will be the
sum of the number of children each node has, which is the total number
of children, which is n-1, which is (another) $Theta;(n) and hence
doesn't change the final answer.
Do a few on the board. As mentioned above, becoming facile with
recursion is vital for tree analyses.
Definition: A traversal is a
systematic way of "visiting" every node in a tree.
Preorder Traversal
Visit the root and then recursively traverse each child. More
formally we first give the procedure for a preorder traversal starting
at any node and then define a preorder traversal of the entire tree as
a preorder traversal of the root.
Algorithm preorder(T,v):
visit node v
for each child c of v
preorder(T,c)
Algorithm preorder(T):
preorder(T,T.root())
Remarks:
- In a preorder traversal, parents come
before children (which is as it should be :-)).
- If you describe a book as an ordered tree, with nodes for each
chapter, section, etc., then the pre-order traversal visits the
nodes in the order they would appear in a table of contents.
Do a few on the board. As mentioned above, becoming facile with
recursion is vital for tree analyses.
Theorem: Preorder traversal of a tree with n nodes
has complexity Θ(n).
Proof:
Just like height.
The nonrecursive part of each invocation takes O(1+cv)
There are n invocations and the sum of the c's is n-1.
Homework: R-2.3
Postorder Traversal
First recursively traverse each child then visit the root.
More formerly
Algorithm postorder(T,v):
for each child c of v
postorder(T,c)
visit node v
Algorithm postorder(T):
postorder(T,T.root())
Theorem: Preorder traversal of a tree with n nodes
has complexity Θ(n).
Proof:
The same as for preorder.
Remarks:
- Postorder is how you evaluate an arithmetic expression tree.
- Evaluate some arithmetic expression trees.
- When you write out the nodes in the order visited your get what is
called either "reverse polish notation" or "polish notation"; I
don't remember which.
- If you do preorder traversal you get the other one.
Problem Set 2, Problem 1.
Note that the height of a tree is the depth of a deepest node.
Extend the height algorithm so that it returns in addition to the
height the v.element() for some v that is of maximal depth. Note that
the height algorithm is for an arbitrary (not necessarily binary)
tree; your extension should also work for arbitrary trees (this is
*not* harder).
2.3.3 Binary Trees
Recall that a binary tree is an ordered tree in which no node has
more than two children. The left child is ordered before the right
child.
The book adopts the convention that, unless otherwise mentioned,
the term "binary tree" will mean "proper binary tree", i.e., all
internal nodes have two children.
This is a little convenient, but not a big deal.
If you instead permitted non-proper binary trees, you would test if a
left child existed before traversing it (similarly for right child.)
We will do binary preorder (first visit the node, then the left
subtree, then the right subtree), binary postorder (left subtree, right
subtree, node) and then inorder (left subtree, node, right subtree).
The Binary Tree ADT
We have three (accessor) methods in addition to the general tree
methods.
- leftChild(v): Return the (position of the) left child; signal an
error if v is a leaf.
- rightChild(v): Similar
- sibling(v): Return the (unique) sibling of v; signal an error if v
is the root (and hence has no sibling).
================ Start Lecture #10 ================
Remark: I will not hold you
responsible for the
proofs of the theorems.
Theorem: Let T be a binary tree having height h
and n nodes. Then
-
The number of leaves in T is at least h+1 and at most 2h.
-
The number of internal nodes in T is at least h and at most
2h-1.
-
The number of nodes in T is at least 2h+1 and at most
2h+1-1.
-
log(n+1)-1≤h≤(n-1)/2
Proof:
-
Induction on n the number of nodes in the tree.
Base case n=1: Clearly true for all trees having only one
node.
Induction hypothesis: Assume true for all trees having at most
k nodes.
Main inductive step: prove the assertion for all trees having k+1
nodes. Let T be a tree with k nodes and let h be the height of T.
Remove the root of T. The two subtrees produced each have no
more than k nodes so satisfy the assertion. Since each has height
at most h-1, each has at most 2h-1 leaves. At least
one of the subtrees has height exactly h-1 and hence has at least
h leaves. Put the original tree back together.
One subtree
has at least h leaves, the other has at least 1, so the original
tree has at least h+1. Each subtree has at most 2h-1
leaves and the original root is not a leaf, so the original has at
most 2h leaves.
-
Same idea. Induction on the number of nodes. Clearly true if T
has one node. Remove the root. At least one of the subtrees is
height h-1 and hence has at least h-1 internal nodes. Each of the
subtrees has height at most h-1 so has at most 2h-1-1
internal nodes. Put the original tree back together. One subtree
has at least h-1 internal nodes, the other has at least 1, so the
original tree has at least h. Each subtree has at most
2h-1-1 internal nodes and the original root is an
internal node, so the original has at most 2(2h-1)+1
= 2h-1-1 internal nodes.
-
Add parts 1 and 2.
-
Apply algebra (including a log) to part 3.
Theorem:In a binary tree T, the number of leaves
is 1 more than the number of internal nodes.
Proof:
Again induction on the number of nodes. Clearly true for one node.
Assume true for trees with up to n nodes and let T be a tree with n+1
nodes. For example T is the top tree on the right.
- Choose a leaf and its parent (which of course is internal).
For example, the leaf t and parent s in red.
- Remove the leaf and its parent (middle diagram)
- Splice the tree back without the two nodes (bottom diagram).
- Since S has n-1 nodes, S satisfies the assertion.
- Note that T is just S + one leaf + one internal so also satisfies
the assertion.
Alternate Proof (does not use the pictures):
- Place two tokens on each internal node.
- Push these tokens to the two children.
- Notice that now all nodes but the root have one token; the root
has none.
- Hence 2*(number internal) = (number internal) + (number leaves) + 1
- Done (slick!)
Corollary:
A binary tree has an odd number of nodes.
Proof:
#nodes = #leaves + #internal = 2(#internal)+1.
Preorder traversal of a binary tree
Algorithm binaryPreorder(T,v)
Visit node v
if T.isInternal(v) then
binaryPreorder(T,T.leftChild(v))
binaryPreorder(T,T.rightChild(v))
Algorithm binaryPretorder(T)
binaryPreorder(T,T.root())
Postorder traversal of a binary tree
Algorithm binaryPostorder(T,v)
if T.isInternal(v) then
binaryPostorder(T,T.leftChild(v))
binaryPostorder(T,T.rightChild(v))
Visit node v
Algorithm binaryPosttorder(T)
binaryPostorder(T,T.root())
Inorder traversal of a binary tree
Algorithm binaryInorder(T,v)
if T.isInternal(v) then
binaryInorder(T,T.leftChild(v))
Visit node v
if T.isInternal(v) then
binaryInorder(T,T.rightChild(v))
Algorithm binaryIntorder(T)
binaryPostorder(T,T.root())
Definition: A binary tree is
fully complete if all the leaves are at the same (maximum)
depth.
This is the same as saying that the sibling of a leaf is a leaf.
Euler tour traversal
Generalizes the above. Visit the node three times, first when
``going left'', then ``going right'', then ``going up''.
Perhaps the words should be ``going to go
left'', ``going to go right'' and ``going to go up''.
These words work for internal nodes. For a leaf you just visit it
three times in a row (or you could put in code to only visit a leaf
once; I don't do this).
It is
called an Euler Tour traversal because an Euler tour of a graph is a
way of drawing each edge exactly once without taking your pen off the
paper. The Euler tour traversal would draw each edge twice but if you
add in the parent pointers, each edge is drawn once.
The book uses ``on the left'', ``from below'', ``on the right''. I
prefer my names, but you may use either.
Algorithm eulerTour(T,v):
visit v going left
if T.isInternal(v) then
eulerTour(T,T.leftChild(v))
visit v going right
if T.isInternal(v) then
eulerTour(T,T.rightChild(v))
visit v going up
Algorithm eulerTour(T):
eulerTour(T,T.root))
Pre- post- and in-order traversals are special cases where two of
the three visits are dropped.
It is quite useful to have this three visits.
For example here is a nifty algorithm to print and expression tree
with parentheses to indicate the order of the operations.
We just give the three visits.
Algorithm visitGoingLeft(v):
if T.isInternal(v) then
print "("
Algorithm visitGoingRight(v)
print v.element()
Algorithm visitGoingUp(v)
if T.isInternal(v) then
print ")"
Homework: Plug these in to the Euler Tour and show
that what you get is the same as
Algorithm printExpression(T,v):
input: T an expression tree v a node in T.
if T.isLeaf(v) then
print v.element() // for a leaf the element is a value
else
print "("
printExpression(T,T.leftChild(v))
print v.element() // for an internal node the element is an operator
printExpression(T,T.rightChild(v))
print ")"
Algorithm printExpression(T):
printExpression(T,T.root())
Problem Set 2 problem 2.
We have seen that traversals have complexity Θ(N), where N is
the number of nodes in the tree. But we didn't count the costs of the
visit()s themselves since the user writes that code.
We know that visit() will be called N times, once per node, for post-,
pre-, and in-order traversals and will be called 3N times for Euler
tour traversal. So if each visit costs Θ(1), the total visit cost
will be Θ(N) and thus does not increase the complexity of a
traversal.
If each visit costs Θ(N), the total visit cost will be
Θ(N2) and hence the total traversal cost will be
Θ(N2).
The same analysis works for any visit cost providing all the visits
cost the same. For this problem we will be considering a variable
cost visits. In particular, assume that the cost of visiting a node v
is the height of v (so roots can be expensive to visit, but leaves are
free).
Part A. How many nodes N are in a fully complete binary tree of height
h?
Part B. How many nodes are at height i in a fully complete binary tree
of height h? What is the total cost of visiting all the nodes at
height i?
Part C. Write a formula using ∑ (sum) for the total cost of
visiting all the nodes. This is very easy given B.
One point extra credit. Show that the sum you wrote in part C is
Θ(N).
Part D. Continue to assume the cost of visiting a node equals its height.
Describe a class of binary trees for which the total cost of visiting
the nodes is θ(N2). Naturally these will
not be fully complete binary trees. Hint do problem 3.
2.3.4 Data Structures for representing trees
A vector-based implementation for Binary Trees
We store each node as the element of a vector. Store the root in
element 1 of the vector and the key idea is
that we store the two children of the element at rank r in the
elements at rank 2r and 2r+1.
Draw a fully complete binary tree of height 3 and show where each element
is stored.
Draw an incomplete binary tree of height 3 and show where each
element is stored and that there are gaps.
There must be a way to tell leaves from internal nodes. The book
doesn't make this explicit. Here is an explicit example.
Let the vector S be given. With a vector we have the current size.
S[0] is not used. S[1] has a pointer to the root node (or contains
the root node if you prefer). For each S[i], S[i] is null (a special
value) if the corresponding node doesn't exist). Then to see if the
node v at rank i is a leaf, look at 2i. If 2i exceeds S.size() then v
is a leaf since it has no children. Similarly if S[2i] is null, v is
a leaf. Otherwise v is external.
How do you know that if S[2i] is null, then s[2i+1] will be null?
Ans: Our binary trees are proper.
This implementation is very fast. Indeed all tree operations are
O(1) except for positions() and elements(), which produce n results
and take time Θ(n).
Homework: R-2.7
However, this implementation can waste a lot of space since many of
the entries in S might be unused. That is there may be many i for
which S[i] is null.
Problem Set #2, problem 3.
Give a tree with fewer than 20 nodes for which S.size() exceeds 100.
Give a tree with fewer than 25 nodes for which S.size() exceeds 1000.
Give a tree with fewer than 100 nodes for which S.size() exceeds a
million.
================ Start Lecture #11 ================
Notes.
Vote on midterm date. It can be either next tuesday or next
thurs.
The winner was next thursday 21 Oct.
Final exam is 21 dec 10am. Room TBA.
End of note
Problem Set #2, Problem 4.
Write
Algorithm compareLeaves(T1, T2)
Input: Two binary trees T1 and T2
compareLeaves prints "fewer" if T1 has fewer leaves than T2;
prints "equal" if they have the same number of leaves; and
prints "less" if T1 has more leaves.
Hint: First write
Algorithm countLeaves(T)
Input: A binary tree T.
Another hint countLeaves will probably begin with
countLeaves1(T, T.root(), 0)
(the third parameter is the sum so far).
End of Problem Set #2, Problem 2.
Problem Set #2 assigned. Due in 2 weeks. which is after the
midterm.
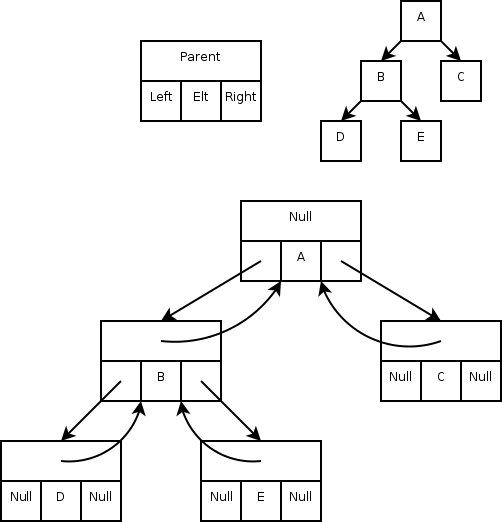
A linked structure for binary trees
Represent each node by a quadruple.
- A reference to the parent (null if we are at the root).
- A reference to the left child (null if at a leaf).
- A reference to the right child (null if at a leaf).
- The element().
Once again the algorithms are all O(1) except for positions() and
elements(), which are Θ(n).
The space is Θ(n) which is much better that for the vector
implementation. The constant is larger however since three pointers
are stored for each position rather than one index.
A linked structure for general trees
The only difference is that we don't know how many children each
node has. We could store k child pointers and say that we cannot
process a tree having more than k children with the same parent.
We don't like limiting the number of children in this way.
Moreover, if we choose k moderate, say k=10. We are limited to 10-ary
trees and for 3-ary trees most of the space is wasted.
So instead of storing the child references in the node, we store
just one reference to a container. The container has references to
the children. Imagine implementing the container as an extendable array.
Since a node v contains an arbitrary number of children, say
Cv, the complexity of the children(v) iterator is
Θ(Cv).
2.4 Priority Queues and Heaps
2.4.1 The Priority Queue Abstract Data Type
Up to now we have not considered elements that must be retrieved in a
fixed order. But often in practice we assign a priority to each item
and want the most important (highest priority) item first.
(For some reason that I don't know, low numbers are often used to
represent high priority.)
For example consider processor scheduling from Operating Systems (202).
The simplest scheduling policy is FCFS for which a queue of ready
processors is appropriate.
But if we want SJF (short job first) then we want to extract the ready
process that has the smallest remaining time.
Hence a FIFO queue is not appropriate.
For a non-computer example,consider managing your todo list. When
you get another item to add, you decide on its importance (priority)
and then insert the item into the todo list.
When it comes time to perform an item, you want to remove the highest
priority item. Again the behavior is not FIFO.
Ordering properties and comparators
To return items in order, we must know when one item is less than
another. For real numbers this is of course obvious.
We assume that each item has a key on which the priority
is to be based. For the SJF example given above, the key is the time
remaining. For the todo example, the key is the importance.
We assume the existence of an order relation (often called a total
order) written ≤
satisfying for all keys s, t, and u.
- "Fully defined" Either s≤t or t≤s.
- Reflexive: s≤s
- Antisymmetric: s≤t and t≤s implies t=s.
- Transitive: s≤t and t≤u implies s≤u.
Remark: For the complex numbers no such ordering exists
that extends the natural ordering on the reals and imaginaries.
This is unofficial (not part of 310).
Is it OK to define s≤t for all s and t?
No. That would not be antisymmetric.
Definition: A priority queue is a
container of elements each of which has an associated key supporting
the following methods.
- InsertItem(k,e): Insert an element e with key k.
- removeMin(): Return and remove an element with a minimal key,
i.e., a key ≤ the key of any other element.
- minElement(): Return an element with minimal key.
- minKey(): Return a minimal key.
Comparators
Users may choose different comparison functions for the same data.
For example, if the keys are the longitude and latitude of cities, one
user may be interested in comparing longitudes and another latitudes.
So we consider a general comparator containing methods.
- isLess(a,b)
- isLessOrEqual(a,b)
- isEqual(a,b)
- isGreater(a,b)
- isGreaterOrEqual(a,b)
- isComparable(a,b)
2.4.2 PQ-Sort, Selection-Sort, and Insertion-Sort
Given a priority queue it is trivial to sort a collection of
elements. Just insert them and then do removeMin to get them in
order.
Written formally this is
Algorithm PQ-Sort(C,P)
Input: an n element sequence C and an empty priority queue P
Output: C with the elements sorted
while not C.isEmpty() do
e←C.removeFirst()
P.insertItem(e,e) // We are sorting on the element itself.
while not P.isEmpty()
C.insertLast(P.removeMin())
So whenever we give an implementation of a priority queue, we are
also giving a sorting algorithm.
Two obvious implementations of a priority queue give well known (but
slow) sorts. A non-obvious implementation gives a fast sort. We
begin with the obvious.
Implementing a priority queue with an unordered sequence
So insertItem() takes Θ(1) time and hence takes Θ(N) to
insert all n items of C. But remove min, requires we go through the
entire list. This requires time Θ(k) when there are k items in
the list. Hence to remove all the items requires
Θ(n+(n-1)+...+1) = Θ(N2) time.
This sorting algorithm is normally called selection
sort since the dominant step is selecting the minimum each time.
Implementing a priority queue with an ordered sequence
Now removeMin() is simple since it is just removeFirst(), which is
Θ(1). (We store the sequence in wrap-around, i.e. mod N, style.)
But insertItem is Θ(k) when there are k items already in the
priority queue since after finding the correct
location in which to insert, one must slide the remaining elements over.
This sorting algorithm is normally called insertion
sort since the dominant effort is inserting each element.
2.4.3 The Heap Data Structure
We now consider the non-obvious implementation of a priority queue
that gives a fast sort (and a fast priority queue).
The idea is to use a tree to store the elements, with the smallest
element stored in the root.
We will store elements only in the internal nodes (i.e., the leaves
are not used). One could imagine an implementation in which the leaves
are not even implemented since they are not used.
We follow the book and draw internal nodes as circles and leaves
(i.e., external nodes) as squares.
Since the priority queue algorithm will perform steps with complexity
Θ(height of tree), we want to keep the height small.
The way to do this is to fully use each level.
 Definition: A binary tree of height h is
complete if the levels 0,...,h-1 contain the maximum
number of elements and on level h-1 all the internal nodes are to the
left of all the leaves.
Definition: A binary tree of height h is
complete if the levels 0,...,h-1 contain the maximum
number of elements and on level h-1 all the internal nodes are to the
left of all the leaves.
Remarks:
- Level i has 2i nodes, for 0≤i≤h-1.
- Level h contains only leaves.
- Levels less than h-1 contain no leaves.
- So really, for all levels, internal nodes are to the left of leaves.
Definition: A tree storing a key at each internal node
satisfies the heap-order property if, for every node v
other than the root, the key at v is no smaller than the key at v's
parent.
Definition: A heap is a complete
binary tree satisfying the heap order property.
Definition: The last node of a
heap is the right most internal node in level h-1.
In the diagrams above the last nodes are pink.
Remark: As written the ``last node'' is really the
last internal node. However, we actually don't use the leaves to
store keys so in some sense ``last node'' is the last (significant) node.
Homework:
R-2.11, R-2.14
Implementing a Priority Queue with a Heap
With a heap it is clear where the minimum is located, namely at the
root. We will also use a reference to the last
node since insertions will occur at the first node after last.
Theorem:
A heap storing n keys has height ⌈log(n+1)⌉
Proof:
-
Let h be the height of the tree and note that n is the number of
internal nodes.
- Levels 0 through h-2 are full and contain only internal nodes (which
contain keys).
- This gives 1+2+4+...+2h-2 keys.
- Homework: Show this is 2h-1-1 keys.
- Level h-1 contains between 1 and 2h-1 internal nodes
each containing a key.
- Level h contains no internal nodes.
- So (2h-1-1)+1 ≤ n ≤ (2h-1-1)+2h-1
- So 2h-1 ≤ n ≤ 2h-1
- So 2h-1 < n+1 ≤ 2h
- So h-1 < log(n+1) ≤ h
- So ⌈log(n+1)&rceil = h
Corollary: If we can implement insert and
removeMin in time Θ(height), we will have implemented the
priority queue operations in logarithmic time (our goal).
Illustrate the theorem with the diagrams above.
The Vector Representation of a Heap
Since we know that a heap is complete, it is efficient to use the
vector representation of a binary tree. We can actually not bother
with the leaves since we don't ever use them. We call the last node w
(remember that is the last internal node). Its index in the vector
representation is n, the number of keys in the heap. We call the
first leaf z; its index is n+1. Node z is where we will insert a new
element and is called the insertion position.
Insertion
This looks trivial. Since we know n, we can find n+1 and hence the
reference to node z in O(1) time.
But there is a problem; the result might not be a heap since the new
key inserted at z might be less than the key stored at u the parent of
z.
Reminiscent of bubble sort, we need to bubble the value in z up to the
correct location.
Up-Heap Bubbling
We compare key(z) with key(u) and swap the items if necessary. In
the diagram on the right we added 45 and then had to swap it with 70.
But now 45 is still less than its parent so we need to swap again.
At worst we need to go all the way up to the
root. But that is only Θ(log(n)) as desired. Let's slow down and
see that this really works.
- We had a heap before we inserted the new element.
- When we insert the new element it can ruin the heap because it is
too small (i.e. smaller than its parent),
- So the blue node is the problem.
- Since blue is smaller than its parent, we swap them. Call the
parent the victim.
- Two nodes have been swapped we have four things to check:
For each of these two nodes we must see that it is not larger
than its new children and not smaller than its new parent.
- The blue node is definitely not larger than its new children:
One child is the victim, which we know is larger than the blue.
The other child was not smaller than the victim so is surely
not smaller than the blue.
- The blue node might be smaller than its new parent. Indeed in
the diagram on the right it is. That is why we have to keep
bubbling up.
- Before we did the insert, we had a heap so at that point the
victim was not larger than all its descendents. But after the
swap, all of the children of the victim were descendents of
the victim before.
- The victim is definitely not smaller than its new parent,
which is the blue.
Great. It works (i.e., is a heap) and there can only be O(log(n))
swaps because that is the height of the tree.
But wait! What I showed is that it only takes O(n) steps. Is
each step O(1)?
Comparing is clearly O(1) and swapping two fixed elements is also
O(1). Finding the parent of a node is easy (integer divide the vector
index by 2). Finally, it is trivial to find the new index for the
insertion point (just increase the insertion point by 1).
================ Start Lecture #12 ================
Note: A practice midterm is on the web.
Remark: It is not as trivial to find the new
insertion point for heaps when using a linked implementation.
Homework: Show the steps for inserting an element
with key 2 in the heap of Figure 2.41.
Removal
Trivial, right? Just remove the root since that must contain an
element with minimum key. Also decrease n by one.
Wrong!
What remains is TWO trees.
We do want the element stored at the root but we must put some
other element in the root. The one we choose is our friend the last node.
But the last node is likely not to be a valid root, i.e. it will
destroy the heap property since it will likely be bigger than one of
its new children. So we have to bubble this one down. It is shown in
pale red on the right and the procedure explained below.
We also need
to find a new last node, but that really is trivial: It is the node
stored at the new value of n.
Down-Heap Bubbling
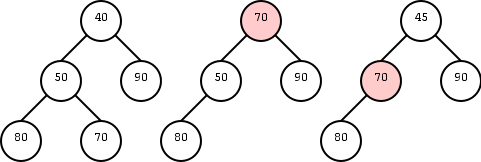
If the new root is the only internal node then we are done.
If only one child of the root is internal (it must be the left
child) compare its key with the key of the root and swap if needed.
If both children of the root are internal, choose the child with
the smaller key and swap with the root if needed.
The original last node, became the root, and now has been bubbled
down to level 1. But it might still be bigger than a child so we keep
bubbling. At worst we need Θ(h) bubbling steps, which is again
logarithmic in n as desired.
Homework: R-2.16
| Operation | Time
|
|---|
| size, isEmpty | O(1)
|
| minElement, minKey | O(1)
|
| insertItem | Θ(log n)
|
| removeMin | Θ(log n)
|
Performance
The table on the right gives the performance of the heap implementation
of a priority queue.
As desired, the main operations have logarithmic time complexity.
It is for this reason that heap sort is fast.
Summary of heaps
- A heap containing n elements is a complete tree T with n internal nodes
each storing a reference to a key and a reference to an element.
The tree also contains n+1 leaves, which are not used.
- The heap is a very fast implementation of a priority queue.
The main operations are logarithmic and the others are constant
time.
- The height of the heap is Θ(log(n)) since T is complete.
- The worst case complexity of the up- and down-heap bubbling
are Θ(height)=Θ(log(n)).
- Finding the insertion position and updating the last node
position take constant time.
-
The insertItem and removeMin operations are Θ(log(n)).
So are minItem and minKey
- Using these insertion and removeMin algorithms makes sorting using
a priority queue fast, i.e., Θ(n*log(n)), as we shall state
officially in the next section.
2.4.4 Heap-Sort (and some extras)
The goal is to sort a sequence S. We return to the PQ-sort where
we insert the elements of S into a priority queue and then use
removeMin to obtain the sorted version. When we use a heap to
implement the priority queue, each insertion and removal takes
Θ(log(n)) so the entire algorithm takes Θ(nlog(n)). The heap
implementation of PQ-sort is called heap-sort and we
have shown
Theorem:
The heap-sort algorithm sorts a sequence of n comparable elements in
Θ(nlog(n)) time.
Implementing Heap-Sort In Place
 In place means that we use the space occupied by the input.
More precisely, it means that the space required is just the input +
O(1) additional memory. The algorithm above required Θ(n)
addition space to store the heap.
In place means that we use the space occupied by the input.
More precisely, it means that the space required is just the input +
O(1) additional memory. The algorithm above required Θ(n)
addition space to store the heap.
The in place heap-sort of S assumes that S is implemented as an
array and proceeds as follows (This presentation, beyond the
definition of ``in place'' is unofficial; i.e., it will not appear on
problem sets or exams)
- Logically divide the array into a portion in the front that
contains the growing heap and the rest that contains the elements
of the array that have not yet been dealt with.
- Initially the heap part is empty and the not-yet-dealt-with
part of the array is the entire array.
- At each insertion we remove the left most entry from the
array part and insert it in the heap, growing the heap to
include the memory previously used by the newly inserted
element. The blue line moves down.
- At the end the heap uses all the space. We are making the
optimization discussed before that we only store the internal
nodes of the heap and do not waste the first (index
0) component of the array used to store the heap.
- Do the insertions a with a normal heap-sort but change the
comparison so that a maximum element is in the root (i.e., a
parent is no smaller than a child).
- Now do the removals from the heap, moving the blue line back up.
- The elements removed are in order big to small.
- This is perfect since we are going to store them starting at
the right of the array since that is the portion of the array
that is made available by the shrinking heap.
Bottom-Up Heap Constructor (unofficial)
If you are given at the beginning all n elements that are to be
inserted, the total insertion time for all inserts can be reduced to
O(n) from O(nlog(n)). The basic idea assuming n=2n-1 is
- Take out the first element and call it r.
- Divide the remaining 2n-2 into two parts each of size
2n-1-1.
- Heap-sort each of these two parts.
- Make a tree with r as root and the two heaps as children.
- Down-heap bubble r.
Locaters (Unofficial)
Sometimes we wish to extend the priority queue ADT to include a
locater that always points to the same element even when the element
moves around. So if x is in a priority queue and another item is
inserted, x may move during the up-heap bubbling, but the locater of x
continues to refer to x.
Comparison of the Priority Queue Implementations
Method
| Unsorted
Sequence
| Sorted
Sequence
|
Heap
|
| size, isEmpty
| Θ(1)
| Θ(1)
| Θ(1)
|
| minElement, minKey
| Θ(n)
| Θ(1)
| Θ(1)
|
| insertItem
| Θ(1)
| Θ(n)
| Θ(log(n))
|
| removeMin
| Θ(n)
| Θ(1)
| Θ(log(n))
|
2.5 Dictionaries and Hash Tables
Dictionaries, as the name implies are used to
contain data that may later be retrieved. Associated with each
element is the key used for retrieval.
For example consider an element to be one student's NYU transcript
and the key would be the student id number. So given the key (id
number) the dictionary would return the entire element (the
transcript).
2.5.1 the Unordered Dictionary ADT
A dictionary stores items, which are key-element
(k,e) pairs.
We will study ordered dictionaries in the next chapter when we
consider searching. Here we consider unordered dictionaries. So, for
example, we do not support findSmallestKey. the methods we do support
are
- findElement(k): Return an element having key k or signal an error if
no such element exists.
- insertItem(k,e): Insert an item with key k and element e.
- removeElement(k): Remove an item with key k and return its
element. Signal an error if no such item exists.
Trivial Implementation: log files
Just store the items in a sequence.
- Trivial (and fast) to insert: Θ(1)
- Minimal space: Θ(n)
- Slow for finding or removing elements: Θ(n) per operation
Remark: The midterm is coming and will be on
chapters 1 and 2. Attend class on monday to vote on the exact day.
2.5.2 Hash Tables
The idea of a hash table is simple: Store the
items in an array (as done for log files) but ``somehow'' be able to
figure out quickly, i.e., Θ(1), which array element contains the item
(k,e).
We first describe the array, which is easy, and then the
``somehow'', which is not so easy. Indeed in some sense it is
impossible. What we can do is produce an implementation that, on the
average, performs operations in time Θ(1).
Bucket Arrays
Allocate an array A of size N of buckets, each able
to hold an item. Assume that the keys are integers in the range
[0,N-1] and that no two items have the same key. Note that N may be
much bigger than n. Now simply store the item (k,e) in A[k].
Analysis of Bucket Arrays
If everything works as we assumed, we have a very fast
implementation: searches, insertions, and removals are Θ(1).
But there are problems, which is why section 2.5 is not finished.
- The keys might not be unique (although in many applications they are):
This is a simple example of a collision.
We discuss collisions in 2.5.5.
- The keys might not be integers: We can always treat any
(computer stored) object as an integer. Just view the object as a
bunch of bits and then consider that a base two non-negative
integer.
- But those integers might not be ``computer integers'', that is,
they might have more bits than the largest integer type in our
programming language: True, we discuss methods for converting long
bit strings into computer integers in 2.5.3.
- But on many machines the number of computer integers is huge. We
can't possibly have a bucket array of size 264: True,
we discuss compressing computer integers into a smaller range in 2.5.4
2.5.3 Hash Functions
We need a hash function h that maps keys to
integers in the range [0,N-1]. Then we will store the item (k,e) in
bucket A[h(k)] (we are for now ignoring collisions). This problem is
divided into two parts. A hash code assigns to each key a computer
integer and then a compression map converts any computer integer into
one in the range [0,N-1]. Each of these steps can introduce
collisions. So even if the keys were unique to begin with, collisions
are an important topic.
Hash Codes
A hash code assigns to any key an integer value.
The problem we have to solve is that the key may have more bits than
are permitted in our integer values. We first view the key as bunch
of integer values (to be explained) and then combine these integer
values into one.
If our integer values are restricted to 32 bits and our keys are 64
bits, we simply view the high order 32 bits as one value and the low
order as another. In general if
⌈numBitsInKey / numBitsInIntegerValue⌉ = k
we view the key as k integer values. How should we combine the k
values into one?
Summing Components
Simply add the k values.
But, but, but what about overflows?
Ignore them (or use exclusive or instead of addition).
Polynomial Hash Codes
The summing components method gives very many collisions when used
for character strings. If 4 characters fill an integer value, then
`temphash' and `hashtemp' will give the same value. If one decided to
use integer values just large enough to hold one (unicode) character,
then there would be many, many common collisions: `t21' and `t12' for
one, mite and time for another.
If we call the k integer values x0,...,xk-1,
then a better scheme for combining is to choose a positive integer
value a and compute
∑xiai=x0+x1a+..xn-1an-1.
Same comment about overflows applies.
The authors have found that using a = 33, 37, 39, or 41
worked well for character strings that are English words.
2.5.4 Compression Maps
The problem we wish to solve in this section is to map integers in
some, possibly large range, into integers in the range [0,N-1].
This is trivial! Why not map all the integers into 0.
We want to minimize collisions.
The Division Method
This is often called the mod method.
One simple way to turn any integer x into one in the range [0,N-1] is
to compute x mod N. That is we define the hash function h by
h(x) = x mod N
(The book uses the funny mod called % in java so must use a slightly
more complicated definition of h. We shall continue to use the
“real” (i.e., mathematical) definition of mod and hence
our definition of h is a little simple.
Choosing N to be prime tends to lower the collision rate, but
choosing N to be a power of 2 permits a faster computation since mod
with a power of two simply means taking the low order bits.
The MAD Method
MAD stands for multiply-add-divide (mod is essentially division).
We still use mod N to get the numbers in the range 0..N-1, but we are a
little fancier and try to spread the numbers out first. Specifically
we define the hash function h via.
h(x) = (ax+b) mod N
The values a and b are chosen (often at random) as positive
integers not a multiple of N.
2.5.5 Collision-Handling Schemes
The question we wish to answer is what to do when two distinct keys
map to the same value, i.e., when h(k)=h(k').
In this case we have two items to store in one bucket.
This discussion also covers the case where we permit multiple items to
have the same key.
Separate Chaining
The idea is simple, each bucket instead of holding an item holds a
reference to a container of items.
That is each bucket refers to the trivial log file implementation of a
dictionary, but only for the keys that map to this container.
The code is simple, you just error check and pass the work off to
the trivial implementation used for the individual bucket.
Algorithm findElement(k):
B←A[h(k)]
if B is empty then
return NO_SUCH_KEY
// now just do the trivial linear search
return B.findElement(k)
Algorithm insertItem(k,e):
if A[h(k)] is empty then
Create B, an empty sequence-based dictionary
A[h(k)]←B
else
B←A[h(k)]
B.insertItem(k,e)
Algorithm removeElement(k)
B←A[h(k)
if B is empty then
return NO_SUCH_KEY
else
return B.removeElement(k)
Homework: R-2.19
================ Start Lecture #13 ================
Load Factors and Rehashing
We don't want many keys to hash to the same given bucket
since the time to find a key at the end of the list is
proportional to the size of the list, i.e., to the number of keys that
hash to this value.
We can't do much about items that have the same key, so we
consider the (common) case where no two items have the same key.
The average size of a list is n/N, called the
load factor, where n is the number of items and N is
the number of buckets.
Typically, one keeps the load factor significantly below
1.0.
The text asserts that 0.75 is common.
What should we do as more items are added to the dictionary?
We make an “extendable dictionary”. That is, as with an extendable
array we double N and “fix everything up” In the case of an
extendable dictionary, the fix up consists of recalculating the hash
of every element (since N has doubled).
In fact no one really calls this an extendable dictionary. Instead
this scheme is referred to as rehashing since, when N is changed, one
must rehash (i.e., recompute the hash) of each element. Also, since
both the old and new N are normally chosen to be a prime number, the
new N can't be obtained doubling the old one.
Instead, the new
N is the smallest prime number exceeding twice the old N.
Open Addressing
Separate chaining involves two data structures: the buckets and the
log files.
An alternative is to dispense with the log files and always store
items in buckets, one item per bucket.
Schemes of this kind are referred to as open
addressing. The problem they need to solve is where to put
an item when the bucket it should go into is already full?
There are several different solutions. We study three: Linear
probing, quadratic probing, and double hashing.
Linear Probing
This is the simplest of the schemes.
To insert a key k (really I should say ``to insert an item (k,e)'') we
compute h(k) and initially assign k
to A[h(k)]. If we find that A[h(k)] contains another key, we assign
k to A[h(k)+1].
It that bucket is also full, we try A[h(k)+2], etc.
Naturally, we do the additions mod N so that after trying A[N-1] we
try A[0]. So if we insert (16,e) into the dictionary at the
right, we place it into bucket 2.
How about finding a key k (again I should say an item (k,e))?
We first look at A[h(k)]. If this bucket contains the key, we have
found it. If not try A[h(k)+1], etc and of course do it mod N (I will
stop mentioning the mod N). So if
we look for 4 we find it in bucket 1 (after encountering two keys
that hashed to 6).
WRONG!
Or perhaps I should say incomplete. What if the item is not on
the list? How can we tell?
Ans: If we hit an empty bucket then the item is not present (if it
were present we would have stored it in this empty bucket). So 20
is not present.
What if the dictionary is full, i.e., if there are no empty
buckets.
Check to see if you have wrapped all the way around. If so, the
key is not present
What about removals?
Easy, remove the item creating an empty bucket.
WRONG!
Why?
I'm sorry you asked. This is a bit of a mess.
Assume we want to remove the (item with) key 19.
If we simply remove it, and search for 4 we will incorrectly
conclude that it is not there since we will find an empty slot.
OK so we slide all the items down to fill the hole.
WRONG! If we slide 6 into the whole at 5, we
will never be able to find 6.
So we only slide the ones that hash to 4??
WRONG! The rule is you slide all keys that are
not at their hash location until you hit an empty space.
Normally, instead of this complicated procedure for removals, we
simple mark the bucket as removed by storing a special value there.
When looking for keys we skip over such slots. When an insert hits
such a bucket, the insert uses the bucket. (The book calls this a
``deactivated item'' object).
Homework: R-2.20
Quadratic Probing
All the open addressing schemes work roughly the same.
The difference is which bucket to try if A[h(k)] is full.
One extra disadvantage of linear probing is that it tends to cluster
the items into contiguous runs, which slows down the algorithm.
Quadratic probing attempts to spread items out by
trying buckets A[h(k)], A[h(k)+1], A[h(k)+4], A[h(k)+9], etc.
One problem is that even if N is prime this scheme can fail to find an
empty slot even if there are empty slots.
Homework: R-2.21
Double Hashing
In double hashing we have two hash functions h and
h'. We use h as above and, if A[h(k)] is full, we try,
A[h(k)+h'(k)], A[h(k)+2h'(k)], A[h(k)+3h'(k)], etc.
The book says h'(k) is often chosen to be (q-k) mod q for some
prime q<N (I use the real mod, the book's definition is in terms of
the java % and is thus more complicated). We will not consider which
secondary hash function h' is good to use.
Homework: R-2.22
Open Addressing vs Separate Chaining
A hard choice. Separate chaining seems to use more space, but that is
deceiving since it all depends on the loading factor.
In general for each scheme the lower the loading factor, the faster
scheme but the more memory it uses.
The key point about both schemes is that the expected time for a
retrieval, insertion, or deletion is Θ(1). We cannot prove this
as it depends on some assumptions about the input distribution and use
more statistics than we assume known.
2.5.6 Universal Hashing (skipped)
2.6 Java Example: Heap (skipped)
================ Start Lecture #14 ================
Midterm Exam
================ Start Lecture #15 ================
Chapter 3 Search Trees and Skip Lists
Last chapter we consider searching in unordered dictionaries.
In general we want to be able to insert, remove, and search
fast.
For unordered dictionaries, where we don't consider an ordering
between keys, the method we learned was hashing.
-
Very fast on average, Θ(1).
-
We can't prove this.
-
Slow in worst case, Θ(N) for N items.
3.1 Ordered Dictionaries and Binary Search Trees
When the keys are ordered, we can also ask for the "next" or
"previous" items.
More precisely we wish to support, in addition to findElement(k),
insertItem(k,e), and removeElement(k), the new methods
-
closestKeyBefore(k): Return the key of the item with largest key
less than or equal to k.
-
closestElemBefore(k): Return the element of the item with largest key
less than or equal to k.
-
closestKeyAfter(k): Return the key of the item with smallest key
greater than or equal to k.
-
closestElemAfter(k): Return the element of the item with smallest key
greater than or equal to k.
We naturally signal an exception if no such item exists. For
example if the only keys present are 55, 22, 77, and 88, then
closestKeyAfter(90) or closestElemBefore(2) each signal an exception.
We begin with the most natural implementation, which however is
slow Θ(N) for inserts and deletes (worst case).
Later we will learn about AVL trees which are fast Θ(log(N))
for all the operations (again worst case).
We will be able to prove the logarithmic bounds. The idea, which
we have seen in heaps, is
-
Use a (binary) tree based data structure.
-
Make sure all operations are Θ(1) on each node visited.
-
Make sure the number of nodes visited is O(height).
-
Make sure the height is O(log(N)). (Since the height of any
binary tree is Ω(log(N)), the height will be
Θ(log(N)).
3.1.1 Sorted Tables
We use the sorted vector implementation from chapter 2 (we used it
as a simple implementation of a priority queue).
Recall that this keeps the items sorted in key order.
Hence it is Θ(n) for inserts and removals, which is slow; however, we
shall see that it is fast for finding and element and for the four new
methods closestKeyBefore(k) and friends.
We call this a lookup table.
The space required is Θ(n) since we grow and shrink the array
supporting the vector
(see extendable arrays).
As indicated the major favorable property of a lookup table is that
it is fast for (surprise) lookups using the binary search algorithm
that we study next.
Binary Search
In this algorithm we are searching for the rank of the item
containing a key equal to k. We are to return a special value if no
such key is found.
The algorithm maintains two variables lo and hi, which are
respectively lower and upper bounds on the rank where k
will be found (assuming it is present).
Initially, the key could be anywhere in the vector so we start
with lo=0 and hi=n-1. We write key(r) for the key at rank r and
elem(r) for the element at rank r.
We then find mid, the rank (approximately) halfway between lo and hi
and see how the key there compares with our desired key.
-
If k = key(mid), we have found the item and return elem(mid)
-
If k < key(mid), then we restrict our attention to indexes less
than mid.
-
If k > key(mid), then we restrict our attention to indexes greater
than mid.
Some care is need in writing the algorithm precisely as it is easy
to have an ``off by one error''. Also we must handle the case in
which the desired key is not present in the vector. This occurs when
the search range has been reduced to the empty set (i.e., when lo
exceeds hi).
Algorithm BinarySearch(S,k,lo,hi):
Input: An ordered vector S containing (key(r),elem(r)) at rank r
A search key k
Integers lo and hi
Output: An element of S with key k and rank between lo and hi.
NO_SUCH_KEY if no such element exits
If lo > hi then
return NO_SUCH_KEY // Not present
mid ← ⌊(lo+hi)/2⌋
if k = key(mid) then
return elem(mid) // Found it
if k < key(mid) then
return BinarySearch(S,k,lo,mid-1) // Try bottom ``half''
if k > key(mid) then
return BinarySearch(S,k,mid+1,hi) // Try top ``half''
Do some examples on the board.
Analysis of Binary Search
It is easy to see that the algorithm does just a few operations per
recursive call. So the complexity of Binary Search is
Θ(NumberOfRecursions). So the question is "How many recursions
are possible for a lookup table with n items?".
The number of eligible items (i.e., the size of the range we still
must consider) is hi-lo+1.
The key insight is that when we recurse, we have reduced the range
to at most half of what it was before. There are two possibilities,
we either tried the bottom or top ``half''. Let's evaluate hi-lo+1
for the bottom and top half. Note that the only two possibilities for
⌊(lo+hi)/2⌋ are (lo+hi)/2 or (lo+hi)/2-(1/2)=(lo+hi-1)/2
Bottom:
(mid-1)-lo+1 = mid-lo = ⌊(lo+hi)/2⌋-lo
≤ (lo+hi)/2-lo = (hi-lo)/2 < (hi-lo+1)/2
Top:
hi-(mid+1)+1 = hi-mid = hi-⌊(lo+hi)/2⌋
≤ hi-(lo+hi-1)/2 = (hi-lo+1)/2
So the range starts at n and is halved each time and remains an
integer (i.e., if a recursive call has a range of size x, the next
recursion will be at most ⌊x/2⌋).
Write on the board 10 times
(X-1)/2 ≤ ⌊X/2⌋ &le X/2
If B ≤ A, then Z-A ≤ Z-B
How many recursions are possible? If the range is ever zero, we
stop (and declare the key is not present) so the longest we can have
is the number of times you can divide by 2 and stay at least 1. That
number is Θ(log(n)) showing that binary search is a logarithmic
algorithm.
Informal Proof:
At each step we lowered the number of possible items from an integer k
to another integer <= k/2. If we look at k in binary the new number
cannot exceed k with the rightmost bit dropped. Since there are only
log(N) bits in N, and we start with N items, we can only perform
log(N) "bit removals".
Problem Set 3, Problem 1
Write the algorithm closestKeyBefore. It uses the same idea as
BinarySearch.
When you do question 1 you will see that the complexity is
Θ(log(n)). Proving this is not hard but is not
part of the problem set.
When you do question 1 you will see that
closestElemBefore, closestKeyAfter, and closestElemAfter are all very
similar to closestKeyBefore. Hence they are all logarithmic
algorithms.
Proving this is not hard but is not
part of the problem set.
Performance Summary of the Array-Based Implementations
Recall that a Log File is an unordered list of items.
| Method | Log File | Lookup Table
|
|---|
| findElement | Θ(n) | Θ(log n)
|
| insertItem | Θ(1) | Θ(n)
|
| removeElement | Θ(n) | Θ(n)
|
| closestKeyBefore | Θ(n) | Θ(log n)
|
| closestElemBefore | Θ(n) | Θ(log n)
|
| closestKeyAfter | Θ(n) | Θ(log n)
|
| closestElemAfter | Θ(n) | Θ(log n)
|
Our goal now is to find a better implementation so that all the
complexities are logarithmic.
This will require us to shift from vectors to trees.
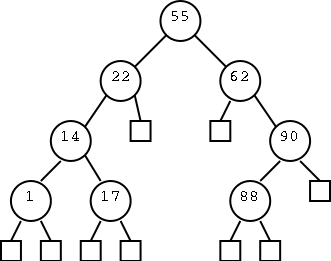
3.1.2 Binary Search Trees
This section gives a simple tree-based implementation, which alas
fails to achieve the logarithmic bounds we seek. But it is a good
start and motivates the AVL trees we study in 3.2 that do achieve the
desired bounds.
Definition: A binary search tree
is a tree in which each internal node v stores an item such that the
keys stored in every node in the left subtree of v are less than or
equal to the key at v which is less than or equal to every key stored
in the right subtree.
From the definition we see easily that an inorder traversal of the
tree visits the internal nodes in nondecreasing order of the keys they
store.
You search by starting at the root and going left or right if the
desired key is smaller or larger respectively than the key at the
current node. If the key at the current node is the key you seek, you
are done. If you reach a leaf the desired key is not present.
Do some examples using the tree on the right. E.g. search for 17,
80, 55, and 65.
Homework: R-3.1 and R-3.2
3.1.3 Searching in a Binary Search Tree
Here is the formal algorithm described above.
Algorithm TreeSearch(k,v)
Input: A search key k and a node v of a binary search tree.
Output: A node w in the subtree routed at v such that either
w is internal and k is stored at w or
w is a leaf where k would be stored if it existed
if v is a leaf then
return v
if k=key(v) then
return v
if k<key(v) then
return TreeSearch(k,T.leftChild(v))
if k>key(v) then
return TreeSearch(k,T.rightChild(v))
Draw a tree on the board and illustrate both finding a k and no
such key exists.
Analysis of Binary Tree Searching
It is easy to see that only a couple of operations are done per
recursive call and that each call goes down a level in the tree.
Hence the complexity is O(height).
So the question becomes "How high is a tree with n nodes?".
As we saw last chapter the answer is "It depends.".
Next section we will learn a technique for keeping trees low.
================ Start Lecture #16 ================
The new methods: closest Key/Item Before/After
Extend the data structure by storing at each node a bit saying
whether this node is the left or right child of its parent.
Problem set #3, problem 2a:
How can we eliminate the bit just introduced?
That is give a Θ(1) algorithm
leftOrRight(T,v)
that determines whether node v of binary tree T is a left or right
child (it signals an error if v is the root).
With the new bit (or with your solution to problem 2a)
we can find the closestKeyBefore (and friends).
 Look at the figure to the right. What should we do if we arrived
at 10 and are
looking for the closest key before 5?
Look at the figure to the right. What should we do if we arrived
at 10 and are
looking for the closest key before 5?
Ans: Get the internal node that occurs just before 10 in a preorder
traversal.
What if we want the closest key before 15?
Ans: It is node 10.
What if we arrived at 30 and wanted closest key before 25?
Ans: It is the node 20.
What if we wanted the closest key before 35?
Ans: It is the node 30?
What if we wanted the closest key after something?
Ans: It is one of 10, 20, 30, or the next internal node after 30 in
a preorder traversal.
To state this in general, assume that we are searching for a key k
that is not present in a binary search tree T.
The search will end at a leaf l. The last key comparison we made was
between k and key(v), with v the parent of l.
 Theorem:
Theorem:
-
If k<key(v) and T.left(v) is a leaf, then
key(w)<k<key(v), where w is the node preceding v in
a preorder traversal (i.e. w is the next smaller node than v).
-
If key(v)<k and T.right(v) is a leaf, then
key(v)<k<key(w), where w is the node following v in
a preorder traversal (i.e., w is the next larger node than v).
Proof: We just prove the first; the second is similar.
We know k<key(v) and w contains the next smaller key.
Note that w must be exactly as shown to the right (the dashed line can
be zero length, i.e. x could be v). Since the search for k reached v,
we went right at w so k>key(w) as desired.
Corollary: Finding the closest Key/Item
Before/After simply requires a search followed by nextInternalInInorder or
prevInternalInInorder.
Problem set #3, problem 2b:
Write the algorithm
nextInternalInInorder(tree T, internal node v)
that finds the next internal node after the internal node v in a
preorder traversal (signal an error if v is the last internal node in
a preorder traversal). You should use the extra bit added above to
determine if a node is a left or right child.
Problem set #3, problem 2c (end of problem 2):
Write an algorithm for the method
closestKeyBefore(k).
3.1.4 Insertion in a Binary Search Tree
To insert an item with key k, first execute
w←TreeSearch(k,T.root()). Recall that if w is internal, k is
already in w, and if w is a leaf, k "belongs" in w. So we proceed as
follows.
- If w is a leaf, replace w with an internal node containing k
(having two leaves as children).
- If w is internal and duplicate keys are not permitted, signal
an error.
- If w is internal and duplicate keys are permitted, call
w=TreeSearch(k,T.leftChild(v)) or w=TreeSearch(k,T.rightChild(v))
and proceed as above.
Draw examples on the board showing both cases (leaf and internal
returned).
Once again we perform a constant amount of work per level of the
tree implying that the complexity is O(height).
3.1.5 Removal in a Binary Search Tree
This is the trickiest part, especially in one case as we describe
below. The key concern is that we cannot simply remove an item from
an internal node and leave a hole as this would make future searches
fail. The beginning of the removal technique is familiar:
w=TreeSearch(k,T.root()). If w is a leaf, k is not present, which we
signal.
If w is internal, we have found k, but now the fun begins.
Returning the element with key k is easy, it is the element
stored in w.
We need to actually remove w, but we cannot leave a hole.
There are three cases.
-
If we are lucky both of w's children are leaves. Then we can
simply replace w with a leaf. (Recall that leaves do not contain
items.) This is the trivial case
-
The next case is when one child of w is a leaf and the other, call
it z, is an internal node.
In this case we can simply replace w by z;
that is have the parent of w now point to z.
This removes w as desired and also removes the leaf child of w,
which is OK since leaves do not contain items.
This is the easy case.
-
Note that the above two cases can be considered the same.
In both cases we notice that one child of w is a leaf and replace
w by the other child (and its descendents, if any).
-
Now we get to the difficult case: both children of w are internal
nodes. What we will do is to replace the item in w with the item
that has the next highest key.
-
First we must find the item with the next highest key.
But that is simply the next item in the inorder traversal.
So we go right and then keep going left until we get a leaf.
The parent of this leaf is the item we seek. Call the parent
y.
-
Store the item in y in the node w. This removes the old
item of w, which we wanted to do.
-
Does the tree still have its items in the correct order?
That is are parents still bigger than (or equal to if we
permit duplicate keys) all of the left subtree and smaller
than all of the right subtree?
-
Yes. The only new parent is the item y which has now
moved to node w. But this is the item right after the old
item in w. Since it came from the right subtree it is
bigger than the left and since it was the smallest in the
right, it is smaller than the right.
-
But what about the old node y? It's left child is a leaf so
it is the easy or trivial case and we just replace y by the
other child and its descendants.
It is again true that the complexity is O(height) but this is
not quite as easy to see as before. We start with a TreeSearch, which
is Θ(height). This gets us to w. The most difficult case is
the last one where w has two internal children. We spend a
non-constant time on node w because we need to find the next item.
But this operation is only O(height) and we simply descend the tree deeper.
3.1.6 Performance of Binary Search Trees
Time complexity of the binary search tree ADT.
We use h for the height and s for the number of elements in the tree.
| Method | Time
|
| size, isEmpty | O(1)
|
| findElement, insertItem, removeElement | O(h)
|
| findAllElements, removeAllElements | O(h+s)
|
We have seen that findElement, insertItem, and removeElement have
complexity O(height). It is also true, but we will not show it, that
one can implement findAllElements and removeAllElements in time
O(height+numberOfElements). You might think removeAllElements should
be constant time since the resulting tree is just a root so we can
make it in constant time. But removeAllElements must also return an
iterator that when invoked must generate each of the elements removed.
Comments on average vs worst case behavior
In a sense that we will not make precise, binary search trees have
logarithmic performance since `most' trees have logarithmic height.
Nonetheless we know that there are trees with height Θ(n).
You produced several of them for problem set #2.
For these trees binary search takes linear time, i.e., is slow. Our
goal now is to fancy up the implementation so that the trees are never
very high. We can do this since the trees are not handed to us.
Instead they are build up using our insertItem method.
================ Start Lecture #17 ================
3.2 AVL Trees
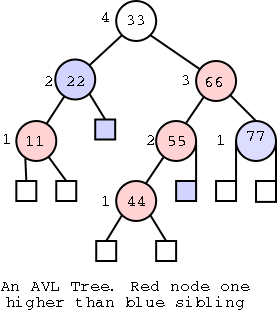
Named after its inventors Adel'son-Vel'skii and Landis.
Definition: An AVL tree is a
binary search tree that satisfies the height-balance
property, which means that for every internal node, the
height of the two children can differ by at most 1.
Homework: Draw an AVL tree of height 3 where each
left child has height one greater than its sibling.
Since the algorithms for an AVL tree require the height to be
computed and this is an expensive operation, each node of an AVL tree
contains its height (say as v.height()).
Remark: You can actually be fancier and store just
two bits to tell whether the node has the same height as its sibling,
one greater, or one smaller.
We see that the height-balance property prevents the tall skinny
trees you developed in problem set 2. But is it really true that the
height must be O(log(n))?
Yes it is and we shall now prove it. Actually we will prove
instead that an AVL tree of height h has at least 2(h/2)-1
internal nodes from which the desired result follows easily.
Lemma: An AVL tree of height h has at least
2(h/2)-1 internal nodes.
Proof:
Let n(h) be the minimum number of internal nodes in an AVL tree of height h.
n(1)=1 and n(2)=2. So the lemma holds for h=1 and h=2.
Here comes the key point.
Consider an AVL tree of height h≥3
and the minimum number of nodes. This tree is composed of a root,
and two subtrees. Since the whole tree has the minimum number of
nodes for its height so do the subtrees. For the big tree to be of
height h, one of the subtrees must be of height h-1. To get the
minimum number of nodes the other subtree is of height h-2.
Why can't the other subtree be of height h-3 or h-4?
The height of siblings can differ by at most 1!
What the last paragraph says in symbols is that for h≥3,
n(h) = 1+n(h-1)+n(h-2)
The rest is just algebra, i.e. has nothing to do with trees,
heights, searches, siblings, etc.
n(h) > n(h-1) so n(h-1) > n(h-2). Hence
n(h) > n(h-1)+n(h-2) > 2n(h-2)
Really we could stop here. We have shown that n(h) at least
doubles when h goes up by 2. This says that n(h) is exponential in h
and hence h is logarithmic in n. But we will proceed slower.
Applying the last formula i times we get
For any i>0, n(h) > 2in(h-2i) (*)
Let's find an i so that h-2i is guaranteed to be 1 or 2.
I claim i = ⌈h/2⌉-1 works.
If h is even h-2i = h-(h-2) = 2
If h is odd h-2i = h - (2⌈h/2⌉-2) = h - ((h+1)-2) = 1
Now we plug this value of i into equation (*) and get for h≥3
n(h) > 2in(h-2i)
= 2⌈h/2⌉-1n(h-2i)
≥ 2⌈h/2⌉-1(1)
≥ 2(h/2)-1
Theorem: the height of an AVL tree storing n items
is O(log(n)).
Proof:
From the lemma we have n(h) > 2(h/2)-1.
Taking logs gives log(n(h)) > (h/2)-1 or
h < 2log(n(h))+2
Since n(h) is the smallest number of nodes possible for an AVL tree of
height h, we see that h < 2 log(n) for any AVL tree of height h.
3.2.1 Update Operations
Insertion
Begin by a standard binary search tree insertion. In the diagrams
on the right, black shows the situation before the insertion; red
after.
The numbers are the heights.
Ignore the blue markings, they are explained in the text as needed.
-
Search the AVL tree for the key to be inserted.
-
Presumably wind up at a leaf (meaning the key not already in the
tree).
-
Call this leaf w.
-
Insert the item by converting w to an internal node at
height one (i.e., the new internal node has two leaves as
children).
-
Call the new internal node w. We view the previous operation as
expanding the leaf w into an internal node (with leaves as
children).
-
In the diagram on the right, w is converted from a black leaf into a
red height 1 node.
Why aren't we finished?
Ans:The tree may no longer be in balance, i.e. it may no longer by an
AVL tree.
We look for an imbalanced node, i.e., a node whose children have
heights differing by more than 1. If we find such a node, the tree is
no longer AVL and we must perform a re-balancing
operation.
-
We start our search for an unbalanced node at w since that is
where the tree has changed. Indeed the height of w has increased
from 0 to 1. This height increase of w may cause
a height increase of w's parent, which in tern may cause a
height increase of w's grandparent, etc. That is, we may need to
search the entire path from w up to the root, i.e. the ancestors
of w. But we know the key fact that no other node has had its
height changed.
-
As we traverse the path from w to the root we will be looking at
the ancestors of w. For each ancestor A we consider, we will also
check the sibling of A. Let h be the height of A before
the insert. Since the tree was AVL before the insert, we know
that the height of A's sibling was and hence is h-1, h, or
h+1. We shall see that these three cases lead us to three
different actions.
-
h-1 will be the "bad" case and will require a re-balancing
operation.
-
h will be the "unknown" case, we will need to proceed up the
tree to see if a re-balance is needed.
-
h+1 will be the "good" case, we will be able to stop and no
re-balancing will be needed.
-
We begin at w which was at height 0 and is now at height 1. Its
children are leaves so w itself is in balance.
-
Since w was at height 0 and the tree was
AVL, its sibling must have had height -1, 0, or +1.
The height of the sibling has not changed (it is not on
the path from w to the root).
Since a height of -1
is impossible, we have just two possibilities, the
“unknown” and “good” cases.
-
If the sibling was at height 1, their parent was, and still
is, at height 2. Hence no heights other than w's changed and
the tree remains in balance. So in this case, which is illustrated
in the figure above, we are indeed done.
-
If the sibling of w was (and hence is) at height 0, we have the
"unknown" case. The siblings heights now differ by 1, which is
OK, but their parent's height has changed from 1 to 2 (since w is
at height 1). This situation is illustrated at the right.
Note that not all
of the tree is shown. Also note that the black heights are before
the insert and the reds are after (ignore the blue for now).
-
Since w's parent P has had its height changed (from 1 to 2) we need
to check P's sibling. The old height is 1 so the sibling must be
at height 0, 1, or 2. (It is 1 in the diagram.) If we had the
"good" case (height=2) the new height of P and the height of P's
sibling would be equal and the height of their parent would not
have changed so we would have been done (without
re-balancing).
-
In the diagram we again have the "unknown" case and proceed up to
P's parent. Another "unknown" case (node's old height and its
siblings height are equal, namely 2) and we keep going up.
-
We get a final unknown case (both heights 3) and finally reach the
root, which was at height 4. Since it has no sibling there is
nothing that can be imbalanced so we are done, again with no
re-balancing required.
-
What is the problem? We just proceed up as in the figure on the
right and eventually we hit the root and are done.
-
WRONG.
-
In the figure, before the insertion, siblings had the same height,
the "unknown" case.
This is certainly possible but not required.
-
If an ancestor of w had height one less than its sibling, then
the insertion has made them equal. That is the "good" case:
The height of the parent doesn't change and we are done as
illustrated in the previous (small) figure.
-
The "bad" case occurs when an ancestor of w had height one greater
than its sibling. In this case the insertion has made it two
greater, which is not permitted for an AVL tree.
-
For example the light blue node could have originally been at
height 2 instead of 3. We no longer have an AVL tree, the root is
imbalanced: Its children have height 2 (the blue) and 4 (the
red). We must re-balance this tree.
The top left diagram illustrates the problem case from the previous
figure (k was 3 above).
-
Node z is the imbalanced ancestor of w found starting at w and
working up. The tree is out of balance, it is no longer
AVL.
-
Node y is the child of z with larger height (it is an ancestor of
w). The old height of y was 1 greater than it sibling's (the
“bad” case). Now it is 2 greater.
-
Node x is the child of y with larger height (it is an ancestor of
w and may in fact equal w). The old height of x was equal to its
sibling's (the “unknown” case). Now it is one
greater.
-
In this diagram y is the right child of z and x is the left child
of y. There are three other possibilities, which are also shown
(but with less detail).
-
We will isolate on the three nodes x y and z and their subtrees
and see how to rearrange the diagram to restore balance.
Definition: The operation we will perform when x,
y, and z lie in a straight line is called a single
rotation. When x, y, and z form an angle, the operation is
called a double rotation.
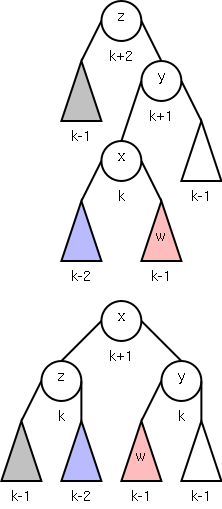 Let us consider the upper left double rotation, which is the rotation
that we need to apply to the example above.
It is redrawn to the right with the subtrees drawn and their heights
after the insertion are listed. The colors are there so that
you can see where they trees go when we perform the rotation.
Let us consider the upper left double rotation, which is the rotation
that we need to apply to the example above.
It is redrawn to the right with the subtrees drawn and their heights
after the insertion are listed. The colors are there so that
you can see where they trees go when we perform the rotation.
Recall that x is
an ancestor of w and has had its height raised from k-1 to k. The
sibling of x is at height k-1 and so is the sibling of y.
The reason x had its height raised is that one of its siblings (say
the right one) has been raised from k-2 to k-1.
How do I know the other one is k-2?
Ans: It must have been the "unknown" case or we would not have
proceeded further up the tree.
The double rotation transforms the picture on top to the one on the
bottom. We now actually are done with the insertion. Let's check the
bottom picture and make sure.
-
The order relation remains intact. That is, every node is greater
than its entire left subtree and less than its entire right
subtree.
-
The tree (now rooted at x) is balanced.
-
Nodes y and z are each at height k. Hence x, the root of this
tree is at height k+1.
-
The tree above, rooted at z, has height k+2.
-
But remember that before the insert z was at height k+1.
-
So the rotated tree (which is after the insert) has the same
height as the original tree before the insert.
-
Hence every node above z in the original tree keeps its original
height so the entire tree is now balanced.
Thus, if an insertion causes an imbalance, just
one rotation re-balances the tree globally.
We will see that for removals it is not this simple.
================ Start Lecture #18 ================
Here are the three pictures for the remaining three possibilities.
That is, the other double rotation and both single rotations. The
original configuration is shown on top and the result after the
rotation is shown immediately below.
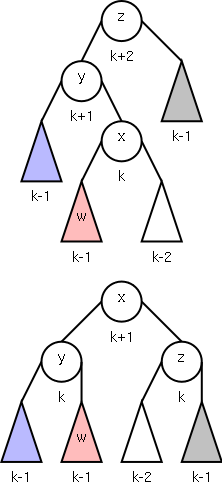
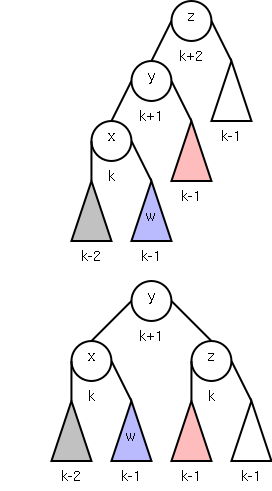
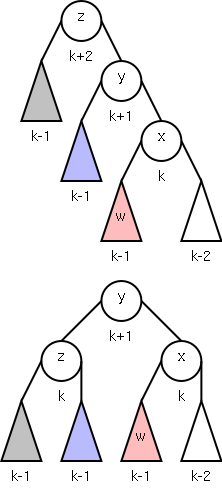
Homework: R-3.3, R-3.4, R-3.5
What is the complexity of insertion?
-
Let n be the number of nodes in the tree before the
insertion.
-
Finding the insertion point is Θ(log n).
-
Expanding the leaf and inserting the item is Θ(1).
-
Walking up the tree looking for an imbalance is Θ(1) per
level, which is O(log n) since the tree has height Θ(log
n).
-
Performing the one needed rotation is
Θ(1).
Hence we have the following
Theorem: The complexity of insertion in an AVL
tree is Θ(log n).
Problem Set 3, problem 3.
Please read the entire problem before beginning.
-
Draw an avl tree containing items with integer keys. Draw the
internal nodes as circles and write the key inside the circle.
Draw the leaves as squares; leaves do not contain items.
You will want to read the remaining parts before drawing this
tree.
-
Choose a key not present in the tree you drew in part A whose
insertion will require the "other" double rotation in order to
restore balance (i.e., the double rotation shown in the diagram
above showing one double and two single rotations).
Draw the tree after the insertion, but prior to the rotation.
Then draw the tree after the rotation.
-
Choose a key not present in the tree you drew in part A whose
insertion will require a single rotation in order to
restore balance.
Draw the tree after the insertion, but prior to the rotation.
Then draw the tree after the rotation.
-
Choose a key not present in the tree you drew in part A whose
insertion will require the "other" single rotation in order to
restore balance
Draw the tree after the insertion, but prior to the rotation.
Then draw the tree after the rotation.
Removing an Item from an AVL Tree
In order to remove an item with key k, we begin just as we did for
an ordinary binary search tree by searching for the item and repairing
the tree. Then we must restore the height-balanced property as we did
when inserting into an AVL tree. Once again rotations are the key,
but there is an extra twist this time. The details follow.
-
Search the AVL tree for the key to be removed.
-
Presumably the search succeeds in finding the key at an internal
node.
If not, the key is not present and we signal an error.
-
Call this internal node w.
-
Returning the element with the desired key is simple; it is the
element at w.
-
We need to actually remove w, but we cannot leave a hole.
We described the procedure previously when discussing removal in a
general binary search tree.
I repeat the discussion here and enhance the pictures since we must
also insure that the resulting tree is balanced (i.e., AVL).
There are you recall three cases.
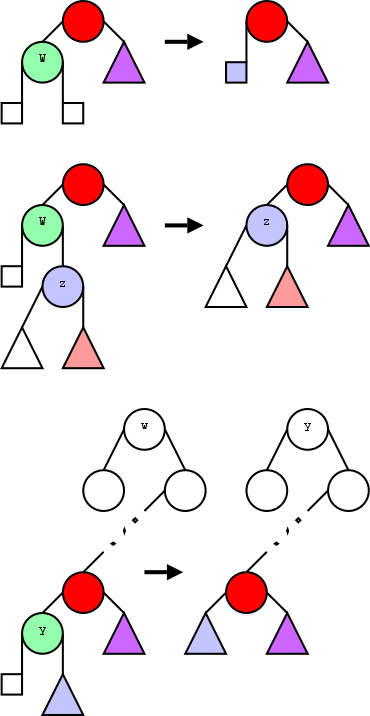
-
The trivial case:
If we are lucky both of w's children are leaves. Then we can
simply replace w with a leaf. (Recall that leaves do not contain
items.) Note that this procedure is the reverse of how we
insert an item.
-
The easy case:
Assume one child of w is a leaf and the other, call
it z, is an internal node.
In this case we can simply replace w by z;
that is have the parent of w now point to z.
This removes w as desired and also removes the leaf child of w,
which is OK since leaves do not contain items.
Note that the above two cases can be considered the same.
We notice that one child of w is a leaf and replace
w by the other child (and its descendents, if any).
-
The difficult case: Both children of w are internal
nodes. What we will do is replace the item in w with the item
that has the next highest key.
-
First we must find the item y with the next highest
key.
We already solved this when we implemented insertions: The
node y we seek is the next internal node after w in an
inorder traversal.
-
Store the item in y in the node w. This removes the old
item of w, which we wanted to do.
-
Does replacing the item in w by the item formerly in y
still result in a binary search tree?
That is, are parents still bigger than (or equal to if we
permit duplicate keys) all of the left subtree and smaller
than all of the right subtree?
-
Yes. The only new parent is the item from y which has
now moved to node w. But this item is the on
immediately after the old item in w. Since it came
from the right subtree of w, it is bigger than the
left subtree, and
since it was the smallest item in the right subtree,
it is smaller than all remaining items in the that
subtree.
-
But what about the old node y? It's left child is a leaf so
it is the easy or trivial case and we just replace y by the
other child and its descendants.
-
We have now successfully removed the item in w and repaired the
structure so that we again have a binary search tree. However, we
may need to restore balance, i.e., re-establish the AVL
property. The possible trouble is that, in each of the three
cases (trivial, easy, or difficult) the light green node on
the left has been replaced by the light blue node on the right, which
is of height one less. This might cause a
problem.
-
Since the tree was balanced before the removal, the sibling of the
light green (shown in purple) had height equal to, one less than,
or one greater than, the height of the light green.
-
If the purple height was equal to the light green, it is now one
greater than the light blue; this is still in balance.
Since the parent (red) has not changed height, all is well.
This is the good case; we are done.
-
If the purple height was one less than the light green, it is
now equal to the light blue; this again remains in balance.
But now red's
height has dropped by one and might be out of balance.
This is the unknown case; we turn our attention to the parent
(red) and redo the balance check.
-
If the purple height was one greater than the light green, it
is now two greater than the light blue so we are out of
balance.
This is the bad case; we must re-balance using a rotation.
-
In the good case we are done; in the unknown case we proceed up
the tree; and in the bad case we rotate.
This sounds the same as for insertion and indeed it is similar, but
there is an important difference.
-
One similarity is that if we proceed up the tree and reach the
root, we are done (there is then no sibling; so we can't be out of
balance).
-
The more important similarity is that the rotations needed are the
same four we used for insertions, two double-rotations and two
single-rotations.
-
The red node is the parent.
-
The purple sibling is the one whose height is too high (I
sometimes called it the “problem” node when
discussing insertions). With removals, heights are decreasing
so the high node is the one whose height was not changed.
-
The third node in the rotation is the higher child of the
purple sibling (or either child, if their heights are equal).
When dealing with insertions we were raising heights, so I
sometimes referred to this child, whose height had been
raised, as the “cause”. For removals, its height
has not changed.
The reason we can use the same rotations for deletions as we used
for insertions is that we are solving the same problem (one
sibling two higher than the other) and, to paraphrase the famous
physicist and lecturer Richard Feynmann, “The same problem
has the same solution”.
-
The important difference is the following.
-
Recall that after a rotation, the highest node has height one less
that the height of the highest node before the rotation (the parent).
For insertions, the parent had just had its height raised by one,
so this reduction restores the height to what it was before the
insertion began. Hence no further changes are needed higher in
the tree.
-
With deletions the highest node after the rotation again has
height one less than the highest node before the rotation, but
there was no previous increase that this reduction cancels.
Hence the height at the top has really been reduced by one, which
can caused this node to be out of balance, depending on whether
its sibling had height that was equal, one larger, or one
greater.
-
If that sibling was equal in height, it is now one greater.
This is in balance and the parent's height is unchanged.
The good case, we are done.
-
If that sibling had height one less, it is now equal.
This is in balance, but the parent's height has dropped by
one.
The unknown case, we move up the tree.
-
If that sibling had height one greater, it is now two
greater.
The bad case, we must perform anotherrotation.
-
This second rotation occurs at a point further up the tree
from the original rotation. Hence even though this second
rotation can cause a third rotation, each subsequent rotation is
closer to the root and at the root the process must stop.
What is the complexity of a removal? Remember that the height of
an AVL tree is Θ(log(N)), where N is the number of nodes.
-
We must find a node with the key, which has complexity
Θ(height) = Θ(log(N)).
-
We must remove the item: Θ(1).
-
We must re-balance the tree, which might involve Θ(height)
rotations. Since each rotation is Θ(1), the complexity is
Θ(log(N))*Θ(1) = Θ(log(N)).
Theorem: The complexity of removal for an AVL tree
is logarithmic in the size of the tree.
Homework: R-3.6
Problem Set 3 problem 4 (end of problem set 3).
Please read the entire problem before beginning.
-
Draw an avl tree containing items with integer keys. Draw the
internal nodes as circles and write the key inside the circle.
Draw the leaves as squares; leaves do not contain items.
You will want to read the remaining parts before drawing this
tree.
-
Choose a key present in the tree you drew in part A whose
removal will require a double rotation and a
single rotation in order to
restore balance.
Draw the tree after the removal, but prior to the rotations.
Then draw the tree after the double rotation, but prior to the
single rotation.
Finally, draw the tree after both rotations.
3.2.2 Performance
The news is good.
Search, Inserting, and Removing all have logarithmic complexity.
The three operations all involve a sweep down the tree searching
for a key, and possibly an up phase where heights are adjusted and
rotations are performed. Since only a constant amount of work is
performed per level and the height is logarithmic, the complexity is
logarithmic.
3.3 Bounded-Depth Search Trees (skipped)
3.4 Splay Trees (skipped)
3.5 Skip Lists (skipped)
3.6 Java Example: AVL and Red-Black Trees (skipped)
Chapter 4 Sorting, Sets, and Selection
We already did a sorting technique in chapter 2.
Namely we inserted items into a priority queue and then removed the
minimum each time.
When we use a heap to implement the priority, the resulting sort is
called heap-sort and is asymptotically optimal.
That is, its complexity of O(Nlog(N)) is as fast as possible if we
only use comparisons (proved in 4.2 below)
4.1 Merge-Sort
4.1.1 Divide-and-Conquer
The idea is that if you divide an enemy into small pieces, each
piece, and hence the enemy, can be conquered.
When applied to computer problems divide-and-conquer
involves three steps.
-
Divide the problem into smaller subproblems.
-
Solve each of the subproblems, normally via a recursive call to
the original procedure.
-
Combine the subproblem solutions into a solution for the original
problem.
In order to prevent an infinite sequence of recursions, we need to
define a stopping condition, i.e., a predicate that informs us when to
stop dividing (because the problem is small enough to solve directly).
Using Divide-and-Conquer for Sorting
This turns out to be so easy that it is perhaps surprising that it
is asymptotically optimal.
The key observation is that merging two sorted lists is fast (the time
is linear in the size of the lists).
The steps are
-
Divide (with stopping condition): If S has zero or one element,
simply return S since it is already sorted.
Otherwise S has n≥2 elements: Move the first ⌈n/2⌉
elements of S into S1 and the remaining
⌊n/2⌋ elements into S2.
-
Solve recursively: Recursively sort each of the two subsequences.
-
Combine: Merge the two (now sorted) subsequences back into S
Example:: Sort {22, 55, 33, 44, 11}.
-
Divide {22, 55, 33, 44, 11} into {22, 55, 33} and {44, 11}
-
Recursively sort {22, 55, 33} and {44, 11} getting {22, 33, 55}
and {11, 44}
-
Merge {22, 33, 55} and {11, 44} getting {11, 22, 33, 44, 55}
Expanding the recursion one level gives.
-
Divide {22, 55, 33, 44, 11} into {22, 55, 33} and {44, 11}
-
Recursively sort {22, 55, 33} and {44, 11} getting {22, 33, 55}
and {11, 44}
-
Divide {22, 55, 33} into {22, 55} and {33}
-
Recursively sort {22, 55} and {33} getting {22, 55} and {33}
-
Merge {22, 55} and {33} getting {22, 33, 55}
-
Divide {44, 11} into {44} and {11}
-
Recursively sort {44} and {11} getting {44} and {11}
-
Merge {44} and {11} getting {11, 44}
-
Merge {22, 33, 55} and {11, 44} getting {11, 22, 33, 44, 55}
Expanding again gives
-
Divide {22, 55, 33, 44, 11} into {22, 55, 33} and {44, 11}
-
Recursively sort {22, 55, 33} and {44, 11} getting {22, 33, 55}
and {11, 44}
-
Divide {22, 55, 33} into {22, 55} and {33}
-
Recursively sort {22, 55} and {33} getting {22, 55} and {33}
-
Divide {22, 55} into {22} and {55}
-
Recursively sort {22} and {55} getting {22} and {55}
-
Merge {22} and {55} getting {22, 55}
-
Do NOT divide {33} since it has only one
element and hence is already sorted
-
Merge {22, 55} and {33} getting {22, 33, 55}
-
Divide {44, 11} into {44} and {11}
-
Recursively sort {44} and {11} getting {44} and {11}
-
Do NOT divide {44} since it has only one
element and hence is already sorted
-
Do NOT divide {11} since it has only one
element and hence is already sorted
-
Merge {44} and {11} getting {11, 44}
-
Merge {22, 33, 55} and {11, 44} getting {11, 22, 33, 44, 55}
Finally there still is one recursion to do so we get.
-
Divide {22, 55, 33, 44, 11} into {22, 55, 33} and {44, 11}
-
Recursively sort {22, 55, 33} and {44, 11} getting {22, 33, 55}
and {11, 44}
-
Divide {22, 55, 33} into {22, 55} and {33}
-
Recursively sort {22, 55} and {33} getting {22, 55} and {33}
-
Divide {22, 55} into {22} and {55}
-
Recursively sort {22} and {55} getting {22} and {55}
-
Do NOT divide {22} since it has only
one element and hence is already sorted.
-
Do NOT divide {55} since it has only
one element and hence is already sorted.
-
Merge {22} and {55} getting {22, 55}
-
Do NOT divide {33} since it has only one
element and hence is already sorted
-
Merge {22, 55} and {33} getting {22, 33, 55}
-
Divide {44, 11} into {44} and {11}
-
Recursively sort {44} and {11} getting {44} and {11}
-
Do NOT divide {44} since it has only one
element and hence is already sorted
-
Do NOT divide {11} since it has only one
element and hence is already sorted
-
Merge {44} and {11} getting {11, 44}
-
Merge {22, 33, 55} and {11, 44} getting {11, 22, 33, 44, 55}
Hopefully there is a better way to describe this action. How about
the following picture. The left tree shows the dividing. The right
shows the result of the merging.
================ Start Lecture #19 ================
Definition: We call the above tree the
merge-sort-tree.
Homework: Draw the merge sort tree for
{55, 33, 11, 22, 44}.
In a merge-sort tree the left and right children of a node with A
elements have ⌈A/2⌉ and ⌊A/2⌋ elements
respectively.
Theorem: Let n be the size of the sequence to be
sorted. If n is a power of 2, say n=2k, then the height of
the merge-sort tree is log(n)=k. In general n = ⌈log(n)⌉.
Proof: The power of 2 case is part of problem set
4. I will do n=2k+1. When we divide the sequence into 2, the
larger is ⌈n/2⌉=2k-1+1: To see this write
2k+1 in binary. When we keep dividing
and look at the larger piece (i.e., go down the leftmost branch of the
tree) we will eventually get to 3=21+1. We have divided by
2 k-1 times so are at depth k-1. But we have to go two more times
(getting 2 and then 1) to get one element. So the depth is of this
element is k+1 and hence the height is at least k+1. The other leaves
are all at height no more than k+1 (in fact they are all k).
Thus the height of the tree is exactly k+1.
The rest is part of problem set 4. Here is the idea. If you
increase the number of elements in the root, you do not decrease the
height. If n is not a power of 2, it is between two powers of 2 and
hence the height is between the heights for these powers of two. My
calculation for 1 more than a power of 2, tells you what the height
must be.
Problem Set 4, problem 1.
Prove the theorem when n is a power of 2.
Prove the theorem for n not a power of 2 either by finishing my
argument or coming up with a new one.
The reason we need the theorem is that we will show that merge-sort
spends time O(n) at each level of the tree and hence spends time
O(n*height) in total. The theorem shows that this is O(nlog(n)).
Merging Two Sorted Sequences
This is quite clear. View each sequence as a deck of cards face up.
Look at the top of each deck and take the smaller card. Keep going.
When one deck runs out take all the cards from the other.
This is clearly constant time per card and hence linear in the number
of cards Θ(#cards).
Unfortunately this doesn't look quite so clear in pseudo code when
we write it in terms of the ADT for sequences. Here is the algorithm
essentially copied from the book. At least the comments are clear.
Algorithm merge(S1, S2, S):
Input: Sequences S1 and S2 sorted in nondecreasing order,
and an empty sequence S
Output: Sequence S contains the elements previously in S1 and S2
sorted in nondecreasing order. S1 and S2 now empty.
{Keep taking smaller first element until one sequence is empty}
while (not(S1.isEmpty() or S2.isEmpty()) do
if S1.first().element()<S2.first().element() then
{move first element of S1 to end of S}
S.insertLast(S1.remove(S1.first())
else
{move first element of S2 to end of S}
S.insertLast(S2.remove(S2.first())
{Now take the rest of the nonempty sequence.}
{We simply take the rest of each sequence.}
{Move the remaining elements of S1 to S
while (not S1.isEmpty()) do
S.insertLast(S1.remove(S1.first())
{Move the remaining elements of S2 to S
while (not S2.isEmpty()) do
S.insertLast(S2.remove(S2.first())
Homework: R-4.2
Examining the code we see that each iteration of each loop removes
an element from either S1 or S2. Hence the total number of iterations
is S1.size()+S2.size(). Since each iteration requires constant time
we get the following theorem.
Theorem: Merging two sorted sequences takes time
Θ(n+m), where n and m are the sizes of the two sequences.
The Running Time of Merge-Sort
We characterize the time in terms of the merge-sort tree. We
assign to each node of the tree the time to do the divide and merge
associated with that node and to invoke (but not to execute) the
recursive calls. So we are essentially charging the node for the
divide and combine steps, but not the solve recursively.
This does indeed account for all the time. Illustrate this with
the example tree I drew at the beginning.
For the remainder of the analysis we assume that the size of the
sequence to be sorted is n, which is a power of 2. It is easy to
extend this to arbitrary n as we did for the theorem that is a part of
problem set 4.
 Now much time is charged to the root? The divide step takes time
proportional to the number of elements in S, which is n. The combine
step takes time proportional to the sum of the number of elements in
S1 and the number of elements in S1. But this is again n. So the
root node is charged Θ(n).
Now much time is charged to the root? The divide step takes time
proportional to the number of elements in S, which is n. The combine
step takes time proportional to the sum of the number of elements in
S1 and the number of elements in S1. But this is again n. So the
root node is charged Θ(n).
The same argument shows that any node is charged Θ(A), where
A is the number of items in the node.
How much time is charged to a child of the root?
Remember that we are assuming n is a power of 2.
So each child has n/2 elements and is charged a constant times n/2.
Since there are two children the entire level is charged Θ(n).
In this way we see that each level is Θ(n).
Another way to see this is that the total number of elements in a
level is always n and a constant amount of work is done on each.
Now we use the theorem saying that the height is log(n) to conclude
that the total time is Θ(nlog(n)). So we have the following
theorem.
Theorem: Merge-sort runs in Θ(nlog(n)).
4.1.2 Merge-Sort and Recurrence Equations
Here is yet another way to see that the complexity is Θ(nlog(n)).
Let t(n) be the worst-case running time for merge-sort on n
elements.
Remark: The worst case and the best case just
differ by a multiplicative constant. There is no especially easy or
hard case for merge-sort.
For simplicity assume n is a power of two. Then we have
for some constants B and C
t(1) = B
t(n) = 2t(n/2)+Cn if n>1
The first line is obvious the second just notes that to solve a
problem we must solve 2 half-sized problems and then do work (merge)
that is proportional to the size of the original problem.
If we apply the second line to itself we get
t(n) = 2t(n/2)+Cn = 2[2t(n/4)+C(n/2)]+Cn =
22t(n/22)+2Cn
If we apply this i times we get
t(n) = 2it(n/2i)+iCn
When should we stop?
Ans: when we get to the base case t(1). This occurs when
2i=n, i.e. when i=log(n).
t(n) = 2log(n)t(n/2log(n)) + log(n)Cn
= nt(n/n) + log(n)Cn since 2log(n)=n
= nt(1) + log(n)Cn
= nB + Cnlog(n)
which again shows that t(n) is Θ(nlog(n)).
4.2 The Set Abstract Data Type (skipped)
4.2.1 A Simple Set Implementation
4.2.2 Partitions with Union-Find Operations
4.2.3 A Tree-Based Partition Implementation
4.3 Quick-Sort
It is interesting to compare quick-sort with merge-sort.
Both are divide and conquer algorithms. So we divide, recursively
sort each piece, and then combine the sorted pieces.
In merge-sort, the divide is trivial: throw half the elements into
one pile and the other half in another pile. The combine step, while
easy does do comparisons and picks an element from the correct pile.
In quick sort the divide is not trivial:
We put all the “small” numbers in one pile and the
“big” numbers in the other.
Thus the combine is trivial: pick up one pile, then the
other.
As usual we assume that the sequence we wish to sort contains no
duplicates. It is easy to drop this condition if desired.
The book's algorithm does quick-sort in place, that is the sorted
sequence overwrites the original sequence. Mine produces a new sorted
sequence and leaves the original sequence alone.
Algorithm quick-sort (S)
Input: A sequence S (of size n).
Output: A sorted sequence T containing the same elements as S.
if n < 2
T ← S
return
Create empty sequences L and G { standing for less and greater }
{ Divide into L and G }
Pick an element P from S { called the pivot }
while (not S.isEmpty())
x ← S.remove(S.first())
if x < P then
L.insertLast(x)
if x > P then
G.insertLast(x)
{ Recursively Sort L and G }
LS ← quick-sort (L) { LS stands for L sorted }
GS ← quick-sort (G)
{ Combine LS, P, and GS }
while (not LS.isEmpty())
T.insertLast(LS.remove(LS.first()))
T.insertLast(P)
while (not GS.isEmpty())
T.insertLast(GS.remove(GS.first()))
Running Time of Quick-Sort
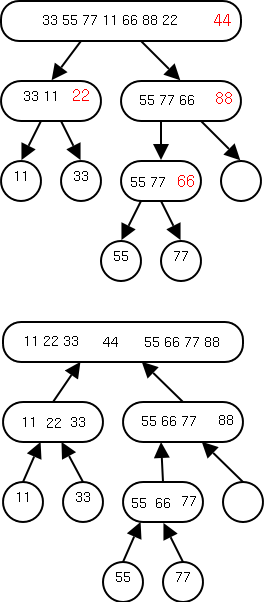 The running time of quick sort is highly dependent on the choice of
the pivots at each stage of the recursion.
A very simple method is to choose the last element as the pivot.
This method is illustrated in the figure on the right. The pivot is
shown in red. This tree is not surprisingly called the
quick-sort tree.
The running time of quick sort is highly dependent on the choice of
the pivots at each stage of the recursion.
A very simple method is to choose the last element as the pivot.
This method is illustrated in the figure on the right. The pivot is
shown in red. This tree is not surprisingly called the
quick-sort tree.
The top tree shows the dividing and recursing that occurs with input
{33,55,77,11,66,88,22,44}.
The tree below shows the combining steps for the same input.
As with merge sort, we assign to each node of the tree the cost
(i.e., running time) of the divide and combine steps. We also assign
to the node the cost of the two recursive calls, but not their
execution. How large are these costs?
The two recursive calls (not including the subroutine execution
itself) are trivial and cost Θ(1).
The dividing phase is a simple loop whose running time is linear in
the number of elements divided, i.e., in the size of the input
sequence to the node. In the diagram this is the number of numbers
inside the oval.
Similarly, the combining phase just does a constant amount of work
per element and hence is again proportional to the number of elements
in the node.
We would like to make an argument something like this. At each
level of each of the trees the total number of elements is n so the
cost per level is O(n). The pivot divides the list in half so the
size of the largest node is divided by two each level. Hence the
number of levels, i.e., the height of the tree, is O(log(n)). Hence
the entire running time is O(nlog(n)).
That argument sounds pretty good and perhaps we should try to make
it more formal. However, I prefer to try something else since the
argument is WRONG!
Homework:
Draw the quick-sort
tree for sorting the following sequence
{222 55 88 99 77 444 11 44 22 33 66 111 333}.
Assume the pivot is always the last element.
================ Start Lecture #20 ================
The Worst Case for Quick-Sort
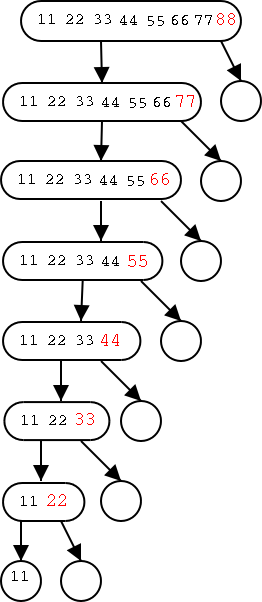 The tree on the right illustrates the worst case of quick-sort, which
occurs when the input is already sorted!
The tree on the right illustrates the worst case of quick-sort, which
occurs when the input is already sorted!
The height of the tree is N-1 not Θ(log(n)). This is because the
pivot is in this case the largest element and hence does not come
close to dividing the input into two pieces each about half the
input size.
It is easy to see that we have the worst case. Since the pivot
does not appear in the children, at least one element from level i
does not appear in level i+1 so at level N-1 you can have at most 1
element left. So we have the highest tree possible.
Note also that level i has at least i pivots missing so can have at
most N-i elements in all the nodes. Our tree achieves this maximum.
So the time needed is proportional to the total number of numbers
written in the diagram which is N + N-1 + N-2 + ... + 1, which is
again the one summation we know N(N+1)/2 or Θ(N2).
Hence the worst case complexity of quick-sort is
quadratic! Why don't we call it slow sort?
Perhaps the problem was in choosing the last element as the pivot.
Clearly choosing the first element is no better; the same example on
the right again illustrates the worst case (the tree has its empty
nodes on the left this time).
Since we are spending linear time (as opposed to constant or
logarithmic time) on the division step, why not count how many
elements are present (say k) and choose element number k/2? This
would not change the complexity (it is also linear). You could do
that and now a sorted list is not the worst case. But some other list
is. Just put the largest element in the middle and then put the
second largest element in the middle of the node on level 1. This
does have the advantage that if you mistakenly run quick-sort on a
sorted list, you won't hit the worst case. But the worst case is
still there and it is still Θ(N2).
Why not choose the real middle element as the pivot, i.e., the
median. That would work! It would cut the sizes in half as desired.
But how do we find the median? We could sort, but that is the
original problem. In fact, there is a (difficult) algorithm for
computing the median in linear time and if this is used for the pivot,
quick-sort does take O(Nlog(N)) time in the worst case. However, the
difficult median algorithm is not fast in practice. That is, the
constants hidden in saying it is Θ(N) are rather large.
Instead of studying the fast, difficult median algorithm, we will
consider a randomized quick-sort algorithm and show that the
expected running time is Θ(Nlog(N)).
Problem Set 4, Problem 2.
Find a sequence of size N=14 giving the worst case for quick-sort when
the pivot for sorting k elements is element number ⌈k/2⌉.
4.3.1 Randomized Quick-Sort
Consider running the following quick-sort-like experiment.
-
Pick a positive integer N
-
Pick a N numbers at random (say without duplicates).
-
Choose at random one of the N numbers and call it the pivot.
-
Split the other numbers into two piles: those bigger than the
pivot and those smaller than the pivot.
-
Call this a good split if the two piles are "nearly" equal.
Specifically, the split is good if the larger of the piles has no
more than 3N/4 elements (which is the same as the smaller pile
having no fewer than N/4 elements)
Are good splits rare or common?
Theorem: (From probability theory). The expected
number of times that a fair coin must be flipped until it shows
``heads'' k times is 2k.
We will not prove this theorem, but will apply it to analyze good
splits.
Theorem: The
expected running time of randomized quick-sort on N
numbers is Θ(Nlog(N)).
Proof: First we prove a little log lemma.
Lemma: logba = log(a) / log(b).
Proof of Lemma: First note that
alog(b) = blog(a) (take the log of both
sides).
Now raise each side to the power 1/log(b).
(alog(b))(1/log(b) =
(blog(a))1/log(b).
Thus a(log(b))/log(b) = b(log(a))/log(b)
(since (xy)z = xyz, see homework below).
So a = b(log(a))/log(b), which says that (log(a))/log(b) is the
power to which one raises b in order to get a. That is the definition of
logba.
End of Proof of Lemma
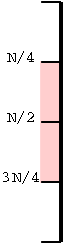 Proof of Theorem:
We picked the pivot at random.
Therefore, if we imagine the
N numbers lined up in order, the pivot is equally likely to be
anywhere in this line.
Proof of Theorem:
We picked the pivot at random.
Therefore, if we imagine the
N numbers lined up in order, the pivot is equally likely to be
anywhere in this line.
Consider the picture on the right.
If the pivot is anywhere in the pink, the split is good.
But the pink is half the line so the probability that we get
a ``pink pivot'' (i.e., a good split) is 1/2.
This is the same probability that a fair coin comes up heads.
Every good split divides the size of the node by at least 4/3.
Recall that if you divide N by 4/3, log4/3(N) times, you
will get 1. So the maximum number of good splits possible along a
path from the root to a leaf is log4/3(N).
Applying the probability theorem above we see that the expected length
of a path from the root to a leaf is at most 2log4/3(N).
By the lemma this is (2log(N))/log(4/3),
which is Θ(log(N)). That is, the expected height is O(log(N)).
Since the time spent at each level is Θ(N), the
expected running time of randomized quick-sort is
O(Nlog(N)).
End of Proof of Theorem
Corollary: The expected running time of randomized
quicksort is Θ(Nlog(N)).
Proof: We just saw that the time is O(Nlog(N)), so
we just need to show it is Ω(Nlog(N)). Since the time on each
level is Θ(N), we need only show that the height is
Ω(Nlog(N)).
Consider a node in the tree with B elements. We divide it into three
piles, the pivot (one element), those less than the pivot, and those
greater than the pivot. The total number in the last two piles is B-1
so the larger of them has at least ⌈(B-1)/2⌉. But, the
transformation B→⌈(B-1)/2⌉ reduces the number of bits
in the binary representation by at most 2 so it takes at least
0.5log(N) iterations to reduce the root, which has N elements to a
level where the largest node has only 1 element. Hence the height is
at least 0.5log(N) as desired.
Homework: Show that
(xy)z = xyz.
Hint take the log of both sides.
4.4 A Lower Bound on Comparison-Based Sorting
Theorem: The running time of any comparison-based
sorting algorithm is Ω(Nlog(N)).
Proof: We will not cover this officially.
Unofficially, the idea is we form a binary tree with each node
corresponding to a comparison performed by the algorithm and the two
children corresponding to the two possible outcomes. This is a tree
of all possible executions (with only comparisons used for decisions).
There are N! permutations of N numbers and each must give a different
execution pattern in order to be sorted. So there are at least N!
leaves. Hence the height is at least log(N!). But N! has N/2
elements that are at least N/2 so N!≥(N/2)N/2. Hence
height ≥ log(N!) ≥ log((N/2)N/2) = (N/2)log(N/2)
So the running time, which is at least the height of this tree, is
Ω(Nlog(N))
Corollary: Heap-sort, merge-sort, and quick sort
(with the difficult, linear-time, not-done-in-class median algorithm)
are asymptotically optimal.
4.5 Bucket-Sort and Radix-Sort
We have seen that the fastest comparison-based sorting algorithms
run in time Θ(Nlog(N)), where N is the number of items to sort.
In this section we are going to develop faster algorithms. Hence they
must not be comparison-based algorithms.
We make a key assumption, we are sorting items whose keys are
integers in a bounded range [0, R-1].
Question: Let's start with a special case R=N so
we are sorting N items with integer keys from 0 to N-1. As usual
we assume there are no duplicate keys. Also as usual we remark that
it is easy to lift this restriction. How should we do this sort?
Answer: That was a trick question. You don't even
have to look at the input. If you tell me to sort 10 integers in the
range 0...9 and there are no duplicates, I know the answer is
{0,1,2,3,4,5,6,7,8,9}. Why? Because, if there are no duplicates, the
input must consist of one copy of each integer from 0 to 10.
4.5.1 Bucket-sort
OK, let's drop the assumption that R=N. So we have N items (k,e),
with each k an integer, no duplicate ks, and 0≤k<R. The trick is
that we can use k to decide where to (temporarily) store e.
Algorithm preBucketSort(S)
input: A sequence S of N items with integer keys in range [0,N)
output: Sequence S sorted in increasing order of the keys.
let B be a vector of R elements,
each initially a special marker indicating empty
while (not S.isEmpty())
(k,e) ← S.remove(S.first())
B[k] ← e <==== the key idea (not a comparison)
for i ← 0 to R-1 do
if (B[i] not special marker) then
S.insertLast((i,B[i])
To convert this algorithm into bucket sort we drop the artificial
assumption that there are not duplicates. Now instead of a vector of
items we need a vector of buckets, where a bucket is a sequence of
items.
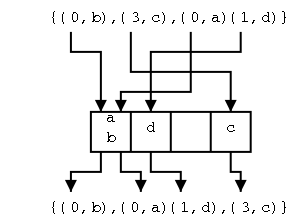
Algorithm BucketSort(S)
input: A sequence S of N items with integer keys in range [0,N)
output: Sequence S sorted in increasing order of the keys.
let B be a vector of R sequences of items
each initially empty
while (not S.isEmpty())
(k,e) ← S.remove(S.first())
B[k].insertLast(e) <==== the key idea
for i ← 0 to R-1 do
while (not B[i].isEmpty())
S.insertLast((i,B[i].remove(B[i].first())))
Complexity of Bucket-Sort
The first loop has N iterations each of which run in time
Θ(1), so the loop requires time Θ(N).
The for loop has R iterations so the while statement is
executed R times. Each while statement requires time Θ(1)
(excluding the body of the while) so all of them require time Θ(N).
The total number of
iterations of all the inner while loops is again N and each again
requires time Θ(1), so the time for all
inner iterations is Θ(N).
The previous paragraph shows that the complexity is
Θ(N)+Θ(R) = Θ(N+R).
So bucket-sort is a winner if R is not too big. For example if
R=O(N), then bucket-sort requires time only Θ(N). Indeed if
R=o(Nlog(N)), bucket-sort is (asymptotically) faster than any
comparison based sorting algorithm (using worst case analysis).
Stable Sorting
Definition: We call a sort stable
if equal elements remain in the same relative position. Stated more
formally: for any two items (ki,ei) and
(kj,ej) such that item
(ki,ei) precedes item
(kj,ej) in S (i.e., i<j), then item
(ki,ei) precedes item
(kj,ej) after sorting as well.
Stability is often convenient as we shall see in the next section
on radix-sort. We note that bucket-sort is stable since we treated
each bucket in a fifo manner inserting at the rear and removing from
the front.
================ Start Lecture #21 ================
4.5.2 Radix-Sort
Let's extend our sorting study from keys that are integers to keys
that are pairs of integers. The first question to ask is, given two
keys (k,m) and (k',m'), which is larger? Note that (k,m) is just the
key; an item would be written ((k,m),e).
Definition:
The lexicographical (dictionary) ordering on pairs of
integers is defined by declaring (k,m) < (k',m') if
either
- k < k' or
- k = k' and m < m'
Note that this really is dictionary order:
canary < eagle < egret < heron
10 < 11 < 12 < 2
Algorithm radix-sort-on-pairs
input: A sequence S of N items with keys
pairs of integers in the range [0,N)
Write elements of S as ((k,m),e)
output: Sequence S lexicographically sorted on the keys
bucket-sort(S) using m as the key
bucket-sort(S) using k as the key
Do an example of radix sorting on pairs.
Do an incorrect sort by starting with the most significant element
of the pair.
Do an incorrect sort by using an individual sort that is not stable.
What if the keys are triples or in general d-tuples?
The answer is ...
Homework: R-4.15
Theorem: Let S be a sequence of N items each of
which has a key (k1,k2,...kd), where
each ki is in integer in the range [0,R). We can sort S
lexicographically in time Θ(d(N+R)) using radix-sort.
4.6 Comparison of Sorting Algorithms
Insertion sort or bubble sort are not suitable for general sorting
of large problems because their running time is quadratic in N, the
number of items. For small problems, when time is not an issue, these
are attractive, because they are so simple.
Also if the input is almost sorted, insertion sort is fast since it
can be implemented in a way that is Θ(N+A), where A is the number of
inversions, (i.e., the number of pairs out of order).
Heap-sort is a fine general-purpose sort with complexity
Θ(Nlog(N)), which is optimal for comparison-based sorting.
Also heap-sort can be executed in place (i.e., without much extra
memory beyond the data to be sorted). (The coverage of in-place
sorting was ``unofficial'' in this course.) If the in-place version
of heap-sort fits in memory (i.e., if the data is less than the size
of memory), heap-sort is very good.
Merge-sort is another optimal Θ(Nlog(N)) sort. It is not
easy to do in place, so is inferior for problems that can fit in
memory. However, it is quite good when the problem is too large to
fit in memory and must be done
``out-of-core''. We didn't discuss this issue,
but the merges can be done with two input and one output file (this is
not trivial to do well, you want to utilize the available memory in
the most efficient manner).
Quick-sort is hard to evaluate. The version with the fast median
algorithm is fine theoretically (worst case again Θ(Nlog(N)),
but is not used because of large constant factors in the fast median.
Randomized quick-sort has a low expected time, but a poor (quadratic)
worst-case time. It can be done in place, and is quite fast on
average in that case, often the fastest. But the quadratic worst case
is a fear (and a non-starter for many real-time applications).
Bucket and radix sort are wonderful when they apply, i.e., when the
keys are integers in a modest range (R a small multiple of N). For
radix sort with d-tuples the complexity is Θ(d(N+R)) so if
d(N+R) is o(Nlog(N)), radix sort is asymptotically faster than
any comparison based sort (e.g., heap-, insertion-,
merge-, or quick-sort).
4.7 Selection (officially skipped; unofficial comments follow)
Selection means the ability to find the kth smallest element.
Sorting will do it, but there are faster (comparison-based) methods.
One example problem is finding the median (N/2 th smallest).
It is not too hard (but not easy) to implement selection with
linear expected time. The surprising and difficult result is that
there is a version with linear worst-case time.
4.7.1 Prune-and-Search
The idea is to prune away parts of the set that cannot contain the
desired element. This is easy to do as seen in the next algorithm.
The less easy part is to show that it takes O(n) expected time.
The hard part is to modify the algorithm so that it takes O(n)
worst case time.
4.7.2 Randomized Quick-Select
Algorithm quickSelect(S,k)
Input: A sequence S of n elements and an integer k in [1,n]
Output: The kth smallest element of S
if n=1 the return the (only) element in S
pick a random element x of X
divide S into 3 sequences
L, the elements of S that are less than x
E, the elements of S that are equal to x
G, the elements of S that are greater than x
{ Now we reduce the search to one of these three sets }
if k≤|L| then return quickSelect(L,k)
if k>|L|+|E| then return quickSelect(G,k-|L|+|E|
return x { We want an element in E; all are equal to x }
4.7.3 Analyzing Randomized Quick-Select (skipped)
4.8 Java Example: In-Place Quick-Sort (skipped)
Chapter 5 Fundamental Techniques
5.1 The Greedy Method
The greedy method is applied to maximization/minimization problems.
The idea is to at each decision point choose the configuration that
maximizes/minimizes the objective function so far.
Clearly this does not lead to the global max/min for all problems, but
it does for a number of problems.
This chapter does not make a good case for the greedy method.
The method is used to solve simple variants of standard problems, but the
the standard variants are not solved with the greedy method. There
are better examples, for example the minimal spanning tree and
shortest path graph problems. The two algorithms chosen for this
section, fractional knapsack and task scheduling, were (presumably)
chosen because they are simple and natural to solve with the greedy
method.
5.1.1 The Fractional Knapsack Method
In the knapsack problem we have a knapsack of a fixed capacity (say
W pounds) and different items i each with a given weight wi and a
given benefit bi. We want to put items into the knapsack so as to
maximize the benefit subject to the constraint that the sum of the
weights must be less than W.
The knapsack problem is actually rather difficult in the normal
case where one must either put an item in the knapsack or not.
However, in this section, in order to illustrate greedy algorithms, we
consider a much simpler variation in which we can take a portion, say
xi≤wi, of an item
and get a proportional part of the benefit.
This is called the
``fractional knapsack problem'' since we can take a fraction of an
item. (The more common knapsack problem is called the ``0-1 knapsack
problem'' since we must either take all (1) or none
(0) of an item).
More formally, for each item i we choose an amount xi
(0≤xi≤wi)
that we will place in the knapsack.
We are subject to the constraint that the sum of the xi is no more
than W since that is all the knapsack can hold.
We desire to maximize the total benefit. Since, for item i,
we only put xi in the knapsack, we don't get the full benefit.
Specifically we get benefit (xi/wi)bi.
But now this is easy!
-
Item i has benefit bi and weighs wi.
-
So its value (per pound) is vi=bi/wi.
-
We make the greedy choice and pick the most valuable item and take
all of it or as much as the knapsack can hold.
-
Then we move to the second most valuable and do the same.
-
This clearly is optimal since it never makes sense to leave over
some valuable item to take some less valuable item.
Why doesn't this work for the normal knapsack problem when we must
take all of an item or none of it?
-
Example: W=6, w1=4, w2=w3=3,
b1=5, b2=b3=3.
-
So v1=5/4, v2=v3=1.
-
Start with the most valuable item, number 1 and put it n the
knapsack.
-
Knapsack can hold 6-4=2 more "pounds" but remaining items won't
fit
-
So the total benefit carried is 5.
-
The right solution is to take items 2 and 3 for a total benefit of
6.
-
The difference between this item and fractional knapsack is that
the knapsack can still hold 2/3 of item 2,
but we can't take part of an item as we can in the fractional
knapsack problem.
Algorithm
algorithm FractionalKnapsack(S,W):
Input: Set S of items i with weight wi and benefit bi all positive.
Knapsack capacity W>0.
Output: Amount xi of i that maximizes the total benefit without
exceeding the capacity.
for each i in S do
xi ← 0 { for items not chosen in next phase }
vi ← bi/wi { the value of item i "per pound" }
w ← W { remaining capacity in knapsack }
while w > 0 and S is not empty
remove from S an item of maximal value { greedy choice }
xi ← min(wi,w) { can't carry more than w more }
w ← w-xi
Analysis
FractionalKnapsack has time complexity O(NlogN) where N is
the number of items in S.
-
The book suggests assuming S is a heap-based priority queue and
then the removal has complexity Θ(logN) so the up to N
removals take O(NlogN). The rest of the algorithm is O(N).
-
Alternatively, S could be a sequence and we could begin
FractionalKnapsack by sorting S with a Θ(NlogN) sort. Now
the removal is simply removing the first element. If we use a
circular list for S, the removal is O(1) so the algorithm is
O(N). Including the sort we again have O(NlogN).
Homework: R-5.1
================ Start Lecture #22 ================
5.1.2 Task Scheduling
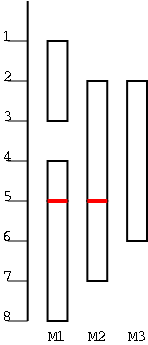
We again consider an easy variant of a well known, but difficult,
optimization problem.
-
We have a set T of N tasks, each with a
start time si and a finishing
time fi (si<fi).
-
Each task must start at time si and will finish at time
fi.
-
Each task is executed on a machine Mj.
-
A machine can execute only one task at a time, but can start a
task at the same time as the current task ends (red lines on the
figure to the right).
-
Tasks are non-conflicting if they do not
conflict, i.e., if fi≤sj or
fj≤si.
For example, think of tasks as college classes.
-
The problem is to schedule all the tasks in T using the minimal
number of machines.
In the figure there are 6 tasks, with start times and finishing
times (1,3), (2,5), (2,6), (4,5), (5,8), (5,7). They are scheduled on
three machines M1, M2, M3. Clearly 3 machines are needed as can be
seen by looking at time 4.
Note that a good solution to this problem has three objectives that
must be met.
-
We must generate a feasible solution. That is, all the
tasks assigned to a single machine are non-conflicting. A
schedule that does not satisfy this condition is invalid
and an algorithm that produces invalid solutions is
wrong.
-
We want to generate a feasible solution using the minimal number
of machines. A schedule that uses more than the minimal number of
machines might be called non-optimal or inefficient and an
algorithm that produces such schedules might be called
poor.
-
We want to generate optimal solutions in the (asymptotically)
smallest amount of time possible. An algorithm that generates
optimal solutions using more time might be called slow.
Let's illustrate the three objectives with following example
consisting of four tasks having starting and stopping times (1,3),
(6,8), (2,5), (4,7). It is easy to construct a wrong algorithm, for
example

Algorithm wrongTaskSchedule(T)
Input: A set T of tasks, each with start time si and
finishing time fi (si≤fi).
Output: A schedule of the tasks.
while T is not empty do
remove from T the first task and call it i.
schedule i on M1
When applied to our 4-task example, the result is all four tasks
assigned to machine 1. This is clearly infeasible since the last two
tasks conflict.
It is also not hard to produce a poor algorithm, one that generates
feasible, but non-optimal solutions.
Algorithm poorTaskSchedule(T):
Input: A set T of tasks, each with start time si and
finishing time fi (si≤fi).
Output: A feasible schedule of the tasks.
m ← 0 { current number of machines }
while T is not empty do
remove from T a task i
m ← m+1
schedule i on Mm
On the 4-task example, poorTaskSchedule puts each task on a
different machine. That is certainly feasible, but is not optimal
since the first and second task can go on one machine.
Hence it looks as though we should not put a task on a new machine
if it can fit on an existing machine. That is certainly a greedy
thing to do. Remember we are minimizing so being greedy really means
being stingy. We minimize the number of machines at each step hoping that
will give an overall minimum. Unfortunately, while better, this idea
does not give optimal schedules. Let's call it mediocre.
Algorithm mediocreTaskSchedule(T):
Input: A set T of tasks, each with start time si and
finishing time fi (si≤fi).
Output: A feasible schedule of the tasks of T
m ← 0 { current number of machines }
while T is not empty do
remove from T a task i
if there is an Mj having all tasks non-conflicting with i then
schedule i on Mj
else
m ← m+1
schedule i on Mm
When applied to our 4-task example, we get the first two tasks on
one machine and the last two tasks on separate machines, for a total
of 3 machines. However, a 2-machine schedule is possible, as we will
shall soon see.
The needed new idea is to processes the tasks in order. Several
orders would work, we shall order them by start time. If two tasks
have the same start time, it doesn't matter which one is put ahead.
For example, we could view the start and finish times as pairs and use
lexicographical ordering. Alternatively, we could just sort on the
first component.
finalAlgorithm
Algorithm taskSchedule(T):
Input: A set T of tasks, each with start time si and
finishing time fi (si≤fi).
Output: An optimal schedule of the tasks of T
m ← 0 { current number of machines }
while T is not empty do
remove from T a task i with smallest start time
if there is an Mj having all tasks non-conflicting with i then
schedule i on Mj
else
m ← m+1
schedule i on Mm
When applied to our 4-task example, we do get a 2-machine solution:
the middle two tasks on one machine and the others on a second.
But is this the minimum? Certainly for this example it is the
minimum; we already saw that a 1-machine solution is not feasible.
But what about other examples?
Correctness (i.e. Minimality of m)
Assume the algorithm runs and declares m to be the minimum number
of machines needed. We must show that m are really needed.
-
Consider the step when the algorithm increases m to its final
value and assume the task under consideration is i.
-
At this point the current task conflicts with one (or more)
task(s) in each of the m-1 machines currently used.
-
But all these tasks have start time no later than si since the
tasks were processed in order of their start time.
-
Since they conflict with i, they each have finishing time after
si.
-
Hence they all conflict with each other as well (consider time
si).
-
Hence we really do need m machines.
OK taskSchedule is feasible and optimal. But is it slow? That
actually depends on some details of the implementation and it does
require a bit of cleverness to get a fast solution.
Complexity
Let N be the number of tasks in T.
The book asserts that it is easy to see that the algorithm runs in
time O(NlogN), but I don't think this is so easy. It is easy to see
O(N2).
-
The while loop has N iterations.
-
If we initially sort the tasks based on their start time (a one
time cost of Θ(NlogN)), the removal is constant time per
iteration or Θ(N) time in total.
-
To figure out the condition part of the if is not trivial.
-
A simple method would be to compare the current task with all
previously scheduled tasks, which shows that the iteration is O(N)
and the algorithm is O(N2).
-
To get O(log(N)) for each iteration, keep the machines
in a heap using as key the latest finishing time assigned to that
machine. This tells you when that machine will be free (remember
that all tasks assigned so far start no later than si, the current
job's start time).
-
Check the min element of the heap. If it is free at si, then it
is free forever starting at si. We now
-
Remove the machine from the heap (removeMin), Θ(logN).
-
Assign the current job to the removed machine, Θ(1).
-
Now this machine is free at fi and we re-insert it
into the heap, Θ(logN).
-
If it is not free at si, then no machine is free at
si so
-
Increase m generating a new machine, Θ(1).
-
Assign i to the new machine m, Θ(1).
-
Insert machine m (which has key fi) into the heap, Θ(logN).
Homework: R-5.3
Problem Set 4, Problem 3.
Part A. C-5.3 (Do not argue why your algorithm is correct).
Part B. C-5.4.
5.2 Divide-and-Conquer
The idea of divide and conquer is that we solve a large problem by
solving a number of smaller problems and then we apply this idea
recursively.
-
Merge Sort and Quick Sort are divide and conquer algorithms.
-
A common example would be that to solve a single problem of size N
we need to solve two problems each of size approximately N/2.
-
When we apply the recursion again, we wind up with four problems
each of size approximately N/4.
-
In addition to the time required to solve the subproblems, we need
to include the time to split the original problem into pieces and
the time required to combine the solutions to the subproblems into
a solution for the original problem.
5.2.1 Divide-and-Conquer Recurrence Equations
From the description above we see that the complexity of a divide
and conquer solution has three parts.
-
The time required to split the problem into subproblems.
-
The time required to solve all the subproblems.
-
The time required to combine the subproblem solutions
Let T(N) be the (worst case) time required to solve an instance of
the problem having time N. The time required to split the problem and
combine the subproblems is also typically a function of N, say f(N).
More interesting is the time required to solve the subproblems. If
the problem has been split in half then the time required for each
subproblem is T(N/2).
Since the total time required includes splitting, solving both
subproblems, and combining we get.
T(N) = 2T(N/2)+f(N)
Very often the splitting and combining are fast, specifically
linear in N. Then we get
T(N) = 2T(N/2)+rN
for some constant r. (We probably should say ≤ rather than =, but
we will soon be using big-Oh and friends so we can afford to be a
little sloppy.)
What if N is not divisible by 2? We should be using floor or
ceiling or something, but we won't. Instead we will be assuming for
recurrences like this one that N is a power of two so that we can keep
dividing by 2 and get an integer. (The general case is not more
difficult; but is more tedious)
But that is crazy! There is no integer that can
be divided by 2 forever and still give an integer! At some point we
will get to 1, the so called base case. But when N=1, the problem is
almost always trivial and has a O(1) solution. So we write either
r if N = 1
T(N) =
2T(N/2)+rN if N > 1
or
T(1) = r
T(N) = 2T(N/2)+rN if N > 1
No we will now see three techniques that, when cleverly applied,
can solve a number of problems. We will also see a theorem that, when
its conditions are met, gives the solution without our being clever.
The Iterative Substitution Method
Also called ``plug and chug'' since we plug the equation into
itself and chug along.
T(N) = 2T(N/2)+rN
= 2[ ]+rN
= 2[2T((N/2)/2)+r(N/2)]+rN
= 4T(N/4)+2rN now do it again
= 8T(N/8)+3rN
A flash of inspiration is now needed. When the smoke clears we get
T(N) = 2iT(N/2i)+irN
When i=log(N), N/2i=1 and we have the base case. This
gives the final result
T(N) = 2log(N)T(N/2log(N))+irN
= N T(1) +log(N)rN
= N r +log(N)rN
= rN+rNlog(N)
Hence T(N) is O(Nlog(N))
The Recursion Tree

The idea is similar but we use a visual approach.
We already studied the recursion tree when we analyzed merge-sort.
Let's look at it again.
The diagram shows the various subproblems that are executed, with
their sizes.
(It is not always true that we can divide the problem so evenly as shown.)
Then we show that the splitting and combining that occur at each node
(plus calling the recursive routine) only take time linear in the
number of elements. For each level of the tree the number of elements
is N so the time for all the nodes on that level is Θ(N) and we
just need to find the height of the tree.
When the tree is split evenly as illustrated the sizes of all the
nodes on each level go down by a factor of two so we reach a node with
size 1 in logN levels (assuming N is a power of 2).
Thus T(N) is Θ(Nlog(N)).
The Guess and Test Method
This method is really only useful after
you have practice in recurrences. The idea is that, when confronted
with a new problem, you recognize that it is similar to a problem you
have seen the solution to previously and you guess that the solution
to the new problem is similar to the old.
You then plug your guess into the recurrence and test that it
works. For example if we guessed that the solution of
T(1) = r
T(N) = 2T(N/2)+rN if N > 1
was
T(N) = rN+rNlog(N)
we would plug it in and check that
T(1) = r
T(N) = 2T(N/2)+rN if N > 1
But we don't have enough experience for this to be very useful.
================ Start Lecture #23 ================
The Master Method
In this section, we apply the heavy artillery. The following
theorem, which we will not prove, enables us to solve some recurrences by
just plugging in. It essentially does the guess part of guess and
test for us.
We will only be considering recurrences of the form
T(1) = c if N < d
T(N) = aT(N/b)+f(N) if N ≥ d
This is admittedly only a small subset of the possible
recurrences.
However, it is not as unimportant as one might think since it fits
very well for the complexity of many divide and conquer algorithms.
The idea is that we have done some sort of divide and conquer where
there are a subproblems of size at
most N/b. As mentioned earlier
f(N) accounts for the time to divide the problem into subproblems and
to combine the subproblem solutions.
What do we do if
T(1) = 7
T(2) = 9
T(3) = 5
T(N) = aT(N/b)+f(N) if N ≥ 4
Not hard.
Just change the algorithm to waste 2 cycles for N=1 and waste 4 cycles
for N=3
Then we have the situation above with c=9 and d=4.
Theorem [The Master Theorem]: Let f(N) and T(N) be
as above.
-
(f is small) If there is a constant ε>0 such that f(N)
is O(Nlogba/nε), then
T(N) is Θ(Nlogba).
-
(f is medium) If there is a constant k≥0 such that f(N) is
θ(Nlogba(logN)k), then
T(N) is θ(Nlogba(logN)k+1).
-
(f is large) If there are constants ε>0 and &delta<1
such that f(N) is
Ω(NlogbaNε) and,
for N≥d, af(N/b)≤δf(N),
then T(N) is Θ(f(N)).
Proof: Not given.
Remarks:
-
When we say f is small/medium/large we are comparing it to the
mysterious Nlogba, which is the star of the
show.
-
So when f is small, T is polynomial; when f is medium, T is
polynomial times a log power; and when f is big, T is f.
-
Nlogba/Nε can also be
written as Nlogba-ε and
NlogbaNε can also be
written as Nlogba+ε.
Now we can solve some problems easily and will do two serious
problems after that.
For all the small examples, assume there are c and d as above (this
only comes up in case three where d appears.
Often in practice (and always on exams in this course) the specific c
and d are not important.
Example: T(N) = 4T(N/2)+N.
-
a=4, b=2, and f(N)=N
-
So Nlogba =
Nlog24 = N2.
-
f is small compared to this. Specifically, f(N) = N =
N2-1; so we are in case 1 with ε=1.
-
Hence T(N) = Θ(Nlogba) =
Θ(N2).
Example: T(N) = 2T(N/2) + Nlog(N)
-
a=2, b=2, and f(N)=Nlog(N)
-
So we have case 2 of the master theorem with k=1.
-
Hence T(N) = Θ(N(logN)2).
We will do all the examples in recitation so will go quickly in class.
Example: T(N) = T(N/4) + 2N
-
a=1, b=4, and f(N)=2N
-
logba = log41 = 0
-
Nlogb = N0 = 1
-
We have case 3 since
f(N) is Ω(N0+ε) for &epsilon=1 and
af(N/b) = (1)2(N/4) = N/2 = (1/4)f(N).
Note that this holds for all N (i.e., the N≥d is not important).
-
Hence T(N) = Θ(N)
Example: T(N) = 9T(N/3) + N2.5
-
a=9, b=3, f(N)=N2.5
-
logba = 2, so Nlogba =
N2
-
We have case 3 since
f(N) is Ω(N2+ε) for &epsilon=.5 and
af(N/b)=9f(N/3)= 9(N/3)2.5=(1/3)0.5f(n).
-
Hence T(n) is O(N2.5)
Example: T(N) = 9T(N/3) + N2
-
a=9, b=3, f(N)=N2
-
logba = 2, so Nlogba =
N2
-
We have case 2 with k=0 since
f(N) is Θ(Nlogba).
-
Hence T(n) is
Θ(N2log(N))
Example: T(N) = 2T(N/2) + rN (our original problem)
-
a=2, b=2, f(N)=rN
-
logba = 1, so Nlogba =
N1 = N.
-
We have case 2 with k=0 since
f(N) is Θ(Nlogba).
-
Hence T(n) is Θ(Nlog(N))
Homework: R-5.4
Problem Set 4, Problem 4.
Let T(N)=125T(N/5)+f(N)
-
Find an f(N) so that case 1 of the master theorem applies.
What is the solution for T(N)?
-
Find an f(N) so that case 2 of the master theorem applies.
What is the solution for T(N)?
-
Find an f(N) so that case 3 of the master theorem applies.
What is the solution for T(N)?
-
Find an f(N) so that no case of the master theorem applies and
explain why no case applies.
End of Problem Set 4, which is now assigned and due 6 Dec.
================ Start Lecture #24 ================
5.2.2 Integer Multiplication
We want to multiply big integers.
When we multiply without machine help, we use as knowledge the
multiplication and addition tables for all 1 digit numbers. In some sense our
``internal computer'' has as primitive operations the multiplication
and addition of two 1-digit number.
To multiply larger numbers, we apply the
5th-grade algorithm that requires Θ(N2) steps to
multiply two N-digit numbers.
Computers typically have a single instruction to
multiply two 32-bit
numbers (or 64-bit on some machines). One way to enable a computer to
multiply two
32N-bit numbers would be to implement the 5-th grade
algorithm in software (using 32-bit numbers as ``digits'') and again
compute the result in Θ(N2) time.
To make the wording easier let's consider the simpler case where
the primitive operations deal with
1-bit numbers and we want to multiply two N-bit numbers X and Y.
We also assume that N is a power of 2.
As we said above, using the 5th grade algorithm we can perform the
multiplication in time
Θ(N2). We want to go faster.
If we simply split each of the N-bit numbers into two pieces,
the high order N/2 bits, and the low
order N/2 bits, we see that to multiply X and Y we need to compute 4
sub-products
Xhi*Yhi, Xhi*Ylo, Xlo*Yhi, Xlo*Ylo.
The 5th grade algorithm specifies that we must put them in the correct
"columns" and add.
Xhi Xlo
x Yhi Ylo
-----------------------
Xhi*Ylo Xlo*Ylo
Xhi*Yhi Xlo*Yhi
Since addition of K-bit numbers is Θ(K) using the 3rd grade
algorithm, and our multiplications
are of N/2-bit values we get
T(N) = 4T(N/2)+cN
We now excitedly apply the master theorem.
The star of the show is
Nlog24=N2.
Thus f(N)=cN is "small" and we are in case 1.
This immediately gives us the answer, which is
T(N)=Θ(N2).
Unfortunately, that is no better than the original 5th grade
algorithm, so we need to try again.
With cleverness are able to get by with three instead
of four multiplications at the cost of some extra additions (and
subtractions, which are treated as additions).
We compute Xhi*Yhi and Xlo*Ylo as before, but then compute the
miraculous (Xhi-Xlo)*(Ylo-Yhi).
Please note that this is one multiplication (i.e., we do the
subtractions first).
The miracle multiplication produces the two
remaining terms we need, but has added to this two other terms.
However, however
those terms are just the (negative of) the two terms we did compute so we
can add them back and they cancel.
Do this on the board.
The summary is that T(N) = 3T(N/2)+cN.
(This c is larger than the one we had before.)
Now the star of the master theorem show is
Nlog23.
Again f(N) is small and we can apply case 1 to get
T(N) = Θ(Nlog23N)
Since log23<1.585, we get the surprising
Theorem: We can multiple two N-bit numbers in
o(N1.585) time.
Homework: R-5.5
5.2.3 Matrix Multiplication
If you thought the integer multiplication involved pulling a rabbit
out of our hat, get ready.
This algorithm was a sensation when it was discovered by Strassen.
The standard algorithm for multiplying two NxN matrices is
Θ(N3). We want to do better.
Do a matrix multiplication on the board and show that it is
Θ(N3). One way to see this is to note that each
entry in the product is an inner product. There are
Θ(N2) entries and computing an inner product is
Θ(N).
 First try. Assume N is a power of 2 and break each matrix into 4
parts as shown on the right. Then X = AE+BG and similarly for Y, Z,
and W. This gives 8 multiplications of half size matrices plus
Θ(N2) scalar addition so
First try. Assume N is a power of 2 and break each matrix into 4
parts as shown on the right. Then X = AE+BG and similarly for Y, Z,
and W. This gives 8 multiplications of half size matrices plus
Θ(N2) scalar addition so
T(N) = 8T(N/2) + bN2
We apply the master theorem and get T(N) = Θ(N3),
i.e., no improvement.
But strassen found the way! He (somehow, I don't know how) decided
to consider the following 7 (not 8) multiplications of half size
matrices.
S1 = A(F-H) S2 = (A+B)H S3 = (C+D)E S4 = D(G-E)
S5 = (A+D)(E+H) S6 = (B-D)(G+H) S7 = (A-C)(E+F)
Now we can compute X, Y, Z, and W from the S's
X = S5+S6+S4-S2 Y = S1+S2 Z = S3+S4 W = S1-S7-S3+S5
This computation shows that
T(N) = 7T(N/2) + bN2
Thus the master theorem now gives
Theorem(Strassen): We can multiply two NxN
matrices in time O(nlog7).
Remarks:
-
log7<2.808 so we can multiply NxN matrices in time
o(N2.808), which is o(N3). Amazing.
-
There are even better algorithms, which are more complicated. I
think they break the matrix into more pieces. The current best is
O(N2.376).
Homework: R-5.6
5.3 Dynamic Programming
This is a little hard to explain abstractly.
One idea is that we compute a max by maximizing over a bunch of
smaller possibilities (and apply this recursively). We then compute
these maxima backwards. That is, instead of breaking the big one into
small ones, we start with the small ones.
Another idea is that we save many intermediate results since they
will be reused. So we really should analyze the space complexity as
well as the time complexity.
5.3.1 Matrix Chain-Product
In this problem we want to multiple n matrices
A0 * A1 * ... * An-1
Unlike the matrix multiplication from last lecture, these matrices
are not all of the same size. But to be able to multiply the
matrices, the number of columns in Ai must be the same as the number
of rows in the next matrix Ai+1.
Specifically Ai is of size di by di+1.
Matrix multiplication is associative, that is
X * (Y * Z) = (X * Y) * Z
Hence in computing the matrix chain-product above, we can do the
multiplications is any order we want and get the same answer. Perhaps
surprisingly, some orders are much faster than others.
Example: Consider A * B * C where
A is a 20x60 matrix
B is a 60x50 matrix
C is a 50x10 matrix
First we perform the computation as A * (B * C).
B * C requires 50 multiplications for each entry in the output.
Since the output is 60x10, there are 600 entries and hence 30,000
multiplications are required to produce the 60x10 result.
We now must multiple A by this new 60x10 matrix. This matrix
product requires 60 multiplications for each entry in the output.
Since the output is 20x10, there are 200 entries and hence 12,000
multiplications are required. So the overall computation requires
42,000 multiplications.
Now we perform the computation as (A * B) * C.
A * B requires 60 multiplications for each entry. Since the output
is 20x50, there are 1000 entries and hence 60,000 multiplications. We
now multiply this result by C. This matrix product requires 50
multiplications for each entry. Since the output is 20x10, there are
200 entries and hence 10,000 multiplications are required. So the
overall computation requires 70,000 multiplication.
 Example:
Do on the board the example on the right. Notice that the answers are
the same for either order of parenthesizing but that the numbers of
multiplications are different.
Example:
Do on the board the example on the right. Notice that the answers are
the same for either order of parenthesizing but that the numbers of
multiplications are different.
================ Start Lecture #25 ================
The matrix chain-product problem is to determine
the parenthesization that minimizes the number of multiplications.
(Obvious) solution. Try every parenthesization and pick the best one.
The obvious solution, often called the brute force
solution, has exponential complexity since the number of ways to
parenthesize an associative expression with n terms is the nth
so-called Catalan number, which is
Ω(4n/n3/2).
We want to do better and will do so using dynamic programming.
We need to define subproblems, subsubproblems, etc and then compute
the answer backwards taking advantage of common subproblems, the
solutions to which we store.
Defining Subproblems
Recall that the matrix product whose multiplications we are trying
to minimize is
A0 * ... * An-1
We want a convenient notation to describe various subproblems and
define Ni,j to be the minimum number of multiplications
needed to compute the subexpression
Ai * ... * Aj
In particular N0,n-1 is the original problem.
Characterizing Optimal Solutions
What follows is the key point of dynamic programming.
The key observation about matrix chain-product is that we can
characterize the optimal solution in terms of optimal solutions of the
subproblems.
(The book calls this the subproblem optimality condition.)
We note specifically that when computing
Ai*...*Aj there must be a last matrix
multiplication so that
Ai*...*Aj = (Ai*...*Ak)*(Ak+1*...*Aj)
and (the KEY point)
to get the minimum number of multiplications for
Ai*...*Aj we must have the minimum number of
multiplications for Ai*...*Ak and for
Ak+1*...Aj.
This says that Ni,j is just the minimum over all possible
k's of
Ni,k + Nk,j + the cost of the final matrix
multiplication.
What is the cost of the final matrix multiplication?
-
The shape of Ai * ... * Ak is
dixdk+1
-
The shape of Ak+1 * ... * Aj is
dk+1xdj
-
Hence dk+1 multiplications are required for each entry
-
The shape of Ai * ... * Aj is
dixdj+1 so there are
didj+1 entries in the product.
-
So the total number of multiplications is
didk+1dj+1
================ Start Lecture #26 ================
Designing a Dynamic Programming Algorithm
We have just seen that
Ni,j = mini≤k<j
{Ni,k + Nk+1,j
+ didk+1dj+1}
Let's call this the fundamental equation.
Although the fundamental equation does not look simple, let's not
be discouraged and keep going. First of all if we apply this
recursively we will get terms in which the subscripts of N are close
together. We can stop the recursion when the subscripts are equal
since Ni,i=0 because no multiplications are required since
no matrix product is being computed.
Remember that the idea of dynamic programming is to run the
recursion backwards and start with the smallest problems.
-
We have Ni,i=0 for all i so the smallest problems are
trivial to solve.
-
What about Ni,i+1?
-
From the fundamental equation this is mini≤k<i+1
{Ni,k + Nk+1,i+1 +
didk+1di+1+1}
-
But there is only one k satisfying i≤k<i+1, namely k=i so we
get that
Ni,i+1 = {Ni,i + Ni+1,i+1 +
didi+1di+2}
-
But Ni,i=0 so we get
Ni,i+1 = {didi+1di+2},
which is the cost of multiplying Ai by Ai+1
-
So we can keep building up Ni,i+g for larger and larger
g, which gives the following algorithm.
algorithm MatrixChain(d0,...,dn) { dynamic programming }
Input: Sequence d0,...,dn of positive integer
corresponding to the dimensions of a chain of matrices
A0,...,An-1
Output: Ni,j, the minimum number of multiplications
needed to compute Ai*...*Aj
for i ← 0 to n-1 do { the simple base case }
Ni,i ← 0
for b ← 1 to n-1 do { keep doing larger gaps }
for i ← 0 to n-1-b { to keep j in bounds )
j ← i+b
{ Calculate Ni,j from the fundamental equation }
Ni,j ← +infinity
for k ← i to j-1 do
Ni,j ← min(Ni,j,Ni,k+Nk+1,j+didk+1dj+1)
This algorithm calculates the minimum number of parenthesis needed
for any contiguous subset of the matrices. In particular
N0,n-1 gives the minimum number of parenthesis needed for
the entire matrix chain-product.
Example: Compute, on the board, the minimum number
of multiplications needed for the example drawn previous. We have
three matrices of shape 2x2, 2x2 and 2x1 respectively so n=3 and the d
vector is 2,2,2,1.
Homework: R-5.9
Analyzing the Matrix Chain-product Algorithm
This is easy now that we know the algorithm.
The algorithm clearly takes O(n3) time since it has a
triply nested loop and each loop has O(n) iterations.
But the algorithm gives the number of parentheses not where they
should be placed. We can fix this problem by storing in
Ni,j not just the number of parentheses but the index k
that gave us the solution.
Theorem: We can compute a parenthesization that
minimizes the number of multiplications in a matrix chain-product in
O(n3) time, where n is the number of matrices.
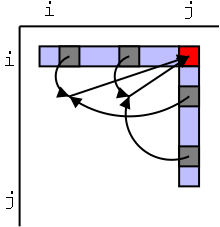 The diagram on the right illustrates the way dynamic program generates
the elements of N.
The diagram on the right illustrates the way dynamic program generates
the elements of N.
-
Remember that the diagonal elements are trivial, they are all
zero.
-
Also remember that everything below the diagonal is not defined:
It's first subscript is larger than its second so it doesn't
corresponding to a sequence of matrices.
-
The diagram gets filled in from the diagonal toward the upper
right. Look in the algorithm and notice that j=i+b so b is the
distance from the diagonal. The algorithm first does b=1, then
b=2, etc.
-
The figure shows the work involved in calculating the red square,
Ni,j. A minimization is taken over k. Two values of k
are illustrated.
-
(k=i+1) Toward the left Ni,i+1 meets
Ni+2,j.
-
(k=i+4) Toward the right Ni,i+4 meets
Ni+5,j.
-
Note that as part of the minimization a product of the d's is
computed. This is not shown in the diagram.
Remark: The space complexity is
Θ(N2) since the only storage used is the array N
(plus a few scalars).
5.3.2 The General Technique
There are three properties needed for successful application of
dynamic programming.
-
Splitting into Subproblems: Must be able to split
the original into subproblems in a recursive manner (i.e., so that
subproblems can also be split into sub-subproblems, etc.). When
the problem is split enough times, easy subproblems must result.
-
Subproblem Optimality: An optimal solution to the
problem must result from optimal solutions to the subproblems via
some simple combining operations.
-
Subproblem Overlap: Many subproblems
themselves contain common sub-subproblems. Thus once we
have solved the sub-subproblem, we can reuse this solution for
many subproblems.
(The following section 5.3.A is not from the book)
5.3.A A java program to show the importance of memoization
We actually made three advances in solving this problem.
-
We found a fairly simple recursive formulation based on singling
out the last matrix multiplication.
-
This recursion has a number of common subproblems (i.e., there is
a great deal of subproblem overlap). If we remember the answer
the first time we solve the subproblem, we can look it up instead
of recomputing it when we encounter this subproblem again. This
is called memoization.
-
We used a dynamic programming solution that starts from small
answers to generate large one. This eliminates the recursion and
makes it easy to see that the solution has cubic complexity.
How important are each of these? I wrote a program that shows that
the gain from 1 to 2 is much more than the gain from 2 to 3.
import java.io.StreamTokenizer;
import java.io.InputStreamReader;
public class MCP
{
static int[] d; // dimension of matrices
static int[][] N; // Hold values in dynamic programming
static boolean[][] known; // Have we memoized this value
static int[][] NN; // Hold memoized values
public static void main (String[] args) throws java.io.IOException
{
StreamTokenizer st =
new StreamTokenizer (new InputStreamReader(System.in));
// Read in data
System.out.println("Enter number of matrices and dimensions:");
st.nextToken();
int n = (int)st.nval;
d = new int[n+1];
for (int i=0; i<=n; i++) {
st.nextToken();
d[i] = (int)st.nval;
}
// Calculate N(0,n-1) recursively
System.out.println ("\nCalculate recursively? [yn]");
st.nextToken();
if (st.sval.equals("y")) {
System.out.println ("Calculating recursively ...");
System.out.println ("... done. The answer is " + NRec(0,n-1));
}
// Calculate N(0,n-1) recursively, but with memoization
System.out.println ("\nCalculate recursively with memoization? [yn]");
st.nextToken();
if (st.sval.equals("y")) {
NN = new int[n][n];
known = new boolean[n][n];
for (int i=0; i< n; i++)
for (int j=0; j < n; j++)
known[i][j] = false;
System.out.println ();
System.out.println ("Calculating N(0,n-1) with memoization ...");
System.out.println ("... done. The answer is " + NRecMemo(0,n-1));
}
// Calculate N(0,n-1) with dynamic programming
System.out.println ("\nCalculate with dynamic programming? [yn]");
st.nextToken();
if (st.sval.equals("y")) {
N = new int[n][n];
System.out.println ();
System.out.println ("Calculating with dynamic programming ...");
System.out.println ("... done. The answer is " + NDyn(n));
}
}
private static int NRec(int i, int j)
{
if (i==j)
return 0;
else {
int ans = Integer.MAX_VALUE;
int val;
for (int k=i; k < j; k++) {
val = NRec(i,k) + NRec(k+1,j) + d[i]*d[k+1]*d[j+1];
if (val < ans)
ans = val;
}
return ans;
}
}
private static int NRecMemo(int i, int j)
{
if (known[i][j])
return NN[i][j];
int ans;
if (i==j)
ans = 0;
else {
ans = Integer.MAX_VALUE;
int val;
for (int k=i; k < j; k++) {
val = NRecMemo(i,k) + NRecMemo(k+1,j) + d[i]*d[k+1]*d[j+1];
if (val < ans)
ans = val;
}
}
NN[i][j] = ans;
known[i][j] = true;
return ans;
}
private static int NDyn(int n)
{
for (int i=0; i < n; i++)
N[i][i]=0;
for (int b=1; b < n; b++)
for (int i=0; i < n-b; i++) {
int j = i+b;
int nij = Integer.MAX_VALUE;
int val;
for (int k=i; k < j; k++) {
val = N[i][k] + N[k+1][j] + d[i]*d[k+1]*d[j+1];
if (val < nij)
nij = val;
}
N[i][j] = nij;
}
return N[0][n-1];
}
}
Let's run the program and see how long it takes.
5.3.3 The 0-1 Knapsack Problem
This is the real knapsack problem, a well-known NP-complete
problem.
A polynomial time algorithm for any NP-complete problem would solve
the leading problem in theoretical computer science.
Finding such an algorithm would ensure its discoverer of a
“Turing Award”, the highest prize in computer science as
well as immediate mention in the NY Times.
So clearly we will not get a polynomial time solution (but
we will get close).
Consider a knapsack that can hold a maximum capacity W and a set S
of n items with item i weighing wi and giving benefit
bi. All the w's, b's and W are positive integers.
The problem is to maximize the benefit of the items carried subject
to the constraint that the total weight cannot exceed W. It is called
the 0-1 knapsack problem because, for each item, you leave it behind
(0) or take all of it (1). You cannot choose to take for example half
of the item as you could in the fractional knapsack problem discussed
at the beginning of this chapter.
Homework: R-5.12
A First Attempt at Characterizing Subproblems
Let Si consist of items 1,2,...,i. So Sn is
all of S.
The idea is that subproblem k will be to find the optimal way to load
the knapsack using only items in Sk, i.e., items 1,...,k.
Then the overall answer is obtained by solving Sn.
It is indeed possible to split the problem this way and when split
enough we get S1, which is trivial to optimize since there
is only one element.
There is subproblem overlap as desired.
But it is not at all clear how to extend an optimal solution found
for Sk to an optimal solution for Sk+1. Indeed
finding the optimal solution for S1, then S2,
then S3, corresponds to deciding on each element one at a
time. This would be a greedy solution and doesn't give a global
optimal.
One could also define Si,j, analogous to Ni,j
above. However, we again don't have a way to extend an optimal
solutions to subproblems into an optimal solution for a bigger
subproblem.
A Better Subproblem Characterization
The problem is that by defining the subproblem simply in terms of
k, we do not get enough information to construct a solution that is
helpful to obtaining a global maximum.
Instead we define subproblems in a more complicated manner. This
is a stroke of inspiration and is not at all obvious.
Let B[k,w] be the maximum benefit obtainable from items in
Sk having total weight exactly w. Our overall
goal is to find B[n,W], the original 0-1 knapsack problem.
This does split the problems into subproblems and when we get down
to B[0,w] we have an trivial problem with solution 0 since we have no
items to select from. (Also B[k,0] is zero since we are not permitted
to choose any items since our weight limit is 0, but we don't use this
fact.)
================ Start Lecture #27 ================
The key that makes this solution work is the observation that
/ B[k-1,w] if wk>w
B[k,w] =
\ max {B[k-1,w], B[k-1,w-wk]+bk} otherwise
This looks formidable, but is not. We need to choose a subset of
the first k items with weight exactly w. If the kth item weighs more
than w, it cannot be used so the best we can do with the first k items
is the same as the best we can do with the first k-1 items. That was
the easier case.
If the kth item is not heavier than w, it can
be used, but need not be (that gives the two possibilities in the
max). If we choose not to use the kth item, we get the previous case
(the first term in the max). If we use the kth item and get total
weight w, the items chosen from the first k-1 must weight
w-wk. Also in this case we gain the benefit of the kth item.
This looks pretty good. We can loop on k and inside that on w.
B[k,*] just depends on B[k-1,*] so it works fine.
Algorithm 01knapsack(S,W)
Input: A set S of n items each with weight wi and benefit bi.
A max weight W. All are positive; all weights integers.
Output: B[k,w] the maximum benefit obtainable from a subset of
the first k items in S having total weight w.
for w ← 0 to W { base case }
B[0,w] ← 0
for k ← 1 to n
for w ← 0 to W
if wk > w then
B[k,w] ← B[k-1,w]
else
B[k,w] = max (B[k-1,w], B[k-1,w-wk]+bk)
Analyzing the 0-1 Knapsack Dynamic Programming Algorithm
This is easy, each loop iteration is constant time so the
complexity is the number of iterations. The base case loop has
Θ(W) iterations and the nested loops have Θ(nW)
iterations.
Thus we get.
Theorem: Given a positive integer W and a set S of
n items each with positive benefit and positive integer weight, we can
find the highest benefit subset of S with total weight at most W in
time Θ(nW).
Remarks:
-
The algorithm given only computes the maximum not the subset. It
is fairly easy to adapt the algorithm to give the items as well
(the max computation tells you weather or not to use item k).
-
My simple program needs space Θ(nW). The book gives a more
subtle argument and an algorithm that only needs space Θ(W).
End of Remarks
I wrote up the knapsack program similar to the matrix chain product
so we can see it run.
Here is the code.
Again the input/output is more code than the computation.
import java.io.StreamTokenizer;
import java.io.InputStreamReader;
import java.lang.Math;
public class Knapsack
{
static int numItems;
static int capacity;
static int[] w; // Weight of items
static int[] b; // Benefit of items
static boolean[][] known; // Have we memoized this value
static int[][] Memo; // Hold memoized values
static int[][] M; // Hold values in dynamic programming
public static void main (String[] args) throws java.io.IOException
{
StreamTokenizer st =
new StreamTokenizer (new InputStreamReader(System.in));
// Read in data
System.out.println("Enter number of items and knapsack capacity:");
st.nextToken();
numItems = (int)st.nval;
st.nextToken();
capacity = (int)st.nval;
System.out.println("Enter positive integers for benefit[1], weight[1], ...");
b = new int[numItems+1]; // b[0] is not used
w = new int[numItems+1]; // w[0] is not used
for (int i=1; i<=numItems; i++) {
st.nextToken();
b[i] = (int)st.nval;
st.nextToken();
w[i] = (int)st.nval;
}
// Calculate recursively
System.out.println ("\nCalculate recursively? [yn]");
st.nextToken();
if (st.sval.equals("y")) {
System.out.println ("Calculating recursively ...");
System.out.println ("... done. The answer is " + KSRec(numItems,capacity));
}
// Calculate N(0,n-1) recursively, but with memoization
System.out.println ("\nCalculate recursively with memoization? [yn]");
st.nextToken();
if (st.sval.equals("y")) {
M = new int[numItems+1][capacity+1];
known = new boolean[numItems+1][capacity+1];
for (int i=0; i no benefit
else {
M[k][weight] = M[k-1][weight]; // don't use item k
if (w[k] <= weight) // try to use item k
M[k][weight] = Math.max (M[k][weight], b[k]+M[k-1][weight-w[k]]);
}
}
}
return M[numItems][capacity];
}
}
Pseudo-Polynomial-Time Algorithms
At first glance the theorem above seems to say that there is a
polynomial time solution to the 0-1 knapsack problem. The time
complexity is Θ(nW), the product of two numbers characteristic of
the input. But this is wrong!
The definition of polynomial time is that the algorithm takes time
that is polynomial in the size of the input. What is the size of the
input?
-
We have n items each with two values a benefit b and a weight w.
We should consider the size of these items to be Θ(n) in
total. That is we should consider each item to be of constant
size since otherwise all the operations we have used are not
constant time. So that means the factor of n in the time
complexity is ok.
-
But what about the factor of W? Well W is an input, doesn't that
settle it? No! The input value W requires only log(W) bits, so
the size of the input W is Θ(log(W)).
-
Hence the input size is &Theta(n+log(W)) and the complexity is
Θ(nW). Is this a polynomial relationship?
-
Consider a big W say W=2n. Then the input size is
Θ(n+n)=Θ(n) and the complexity is
Θ(n2n). So the complexity is exponential in this
case.
-
Indeed for large enough W, nW exceeds the time for the brute-force
solution.
Remark: It is common to refer to algorithms like
ours as requiring pseudo-polynomial time. That is,
the complexity is a polynomial but one or more variables in the
polynomial is one of the input values rather that the size of the
input, which is the size of the binary representation of the input values.
If we originally weighed everything in kilograms and then change to
milligrams, the problem really doesn't change but all the weights are
now 1,000,000 times bigger! This does not effect the recursive
algorithm and does not effect the brute force algorithm.
It clearly effects the full dynamic programming method since W
is a million times larger and we must fill in every item.
At first you would not think that it would effect the memoization
algorithm since we only compute the values that the recursive program
computes and the number of these doesn't change when we shift from
kilograms to milligrams. But this forgets two points
-
Allocating a big matrix can be expensive. For one thing I
had to look up how to run java with a bigger memory pool. I
finally used
java -Xms100m -Xms500m Knapsack
which gives 100MB of initial heap space and 500MB maximum.
-
We have to initialize to false each entry in the known
array (the boolean array used to tell if we already know the
value). We could instead just store the (key,value) pairs in a
hash table or AVL tree. So instead of checking if known[x,y] is
true, we treat (x,y) as the key and do a lookup. If it is there
we have the memoized value. If it is not there we compute and put
it in. If we use AVL, this gives a log(numberOfEntries) cost. If
we use a has table, the worst case is bad.
================ Start Lecture #28 ================
Review


 For queues we need a
front and rear "pointers" f and r. Since we are using arrays f and r
are actually indexes not pointers. Calling the array Q, Q[f] is the
front element of the queue, i.e., the element that would be returned
by dequeue(). Similarly, Q[r] is the element into which enqueue(e)
would place e. There is one exception: if f=r, the queue is empty so
Q[f] is not the front element.
For queues we need a
front and rear "pointers" f and r. Since we are using arrays f and r
are actually indexes not pointers. Calling the array Q, Q[f] is the
front element of the queue, i.e., the element that would be returned
by dequeue(). Similarly, Q[r] is the element into which enqueue(e)
would place e. There is one exception: if f=r, the queue is empty so
Q[f] is not the front element.
 The solution to this problem is to treat the array as circular,
i.e., right after Q[N-1] we find Q[0]. The way to implement this is
to arrange that when either f or r is N-1, adding 1 gives 0 not N.
Similarly for r. So the increment statements become
The solution to this problem is to treat the array as circular,
i.e., right after Q[N-1] we find Q[0]. The way to implement this is
to arrange that when either f or r is N-1, adding 1 gives 0 not N.
Similarly for r. So the increment statements become






 Definition: A binary tree of height h is
complete if the levels 0,...,h-1 contain the maximum
number of elements and on level h-1 all the internal nodes are to the
left of all the leaves.
Definition: A binary tree of height h is
complete if the levels 0,...,h-1 contain the maximum
number of elements and on level h-1 all the internal nodes are to the
left of all the leaves.


 In place means that we use the space occupied by the input.
More precisely, it means that the space required is just the input +
O(1) additional memory. The algorithm above required Θ(n)
addition space to store the heap.
In place means that we use the space occupied by the input.
More precisely, it means that the space required is just the input +
O(1) additional memory. The algorithm above required Θ(n)
addition space to store the heap.



 Look at the figure to the right. What should we do if we arrived
at 10 and are
looking for the closest key before 5?
Look at the figure to the right. What should we do if we arrived
at 10 and are
looking for the closest key before 5? Theorem:
Theorem:





 Let us consider the upper left double rotation, which is the rotation
that we need to apply to the example above.
It is redrawn to the right with the subtrees drawn and their heights
after the insertion are listed. The colors are there so that
you can see where they trees go when we perform the rotation.
Let us consider the upper left double rotation, which is the rotation
that we need to apply to the example above.
It is redrawn to the right with the subtrees drawn and their heights
after the insertion are listed. The colors are there so that
you can see where they trees go when we perform the rotation.





 Now much time is charged to the root? The divide step takes time
proportional to the number of elements in S, which is n. The combine
step takes time proportional to the sum of the number of elements in
S1 and the number of elements in S1. But this is again n. So the
root node is charged Θ(n).
Now much time is charged to the root? The divide step takes time
proportional to the number of elements in S, which is n. The combine
step takes time proportional to the sum of the number of elements in
S1 and the number of elements in S1. But this is again n. So the
root node is charged Θ(n).

 The running time of quick sort is highly dependent on the choice of
the pivots at each stage of the recursion.
A very simple method is to choose the last element as the pivot.
This method is illustrated in the figure on the right. The pivot is
shown in red. This tree is not surprisingly called the
quick-sort tree.
The running time of quick sort is highly dependent on the choice of
the pivots at each stage of the recursion.
A very simple method is to choose the last element as the pivot.
This method is illustrated in the figure on the right. The pivot is
shown in red. This tree is not surprisingly called the
quick-sort tree.
 The tree on the right illustrates the worst case of quick-sort, which
occurs when the input is already sorted!
The tree on the right illustrates the worst case of quick-sort, which
occurs when the input is already sorted!
 Proof of Theorem:
We picked the pivot at random.
Therefore, if we imagine the
N numbers lined up in order, the pivot is equally likely to be
anywhere in this line.
Proof of Theorem:
We picked the pivot at random.
Therefore, if we imagine the
N numbers lined up in order, the pivot is equally likely to be
anywhere in this line.




 First try. Assume N is a power of 2 and break each matrix into 4
parts as shown on the right. Then X = AE+BG and similarly for Y, Z,
and W. This gives 8 multiplications of half size matrices plus
Θ(N2) scalar addition so
First try. Assume N is a power of 2 and break each matrix into 4
parts as shown on the right. Then X = AE+BG and similarly for Y, Z,
and W. This gives 8 multiplications of half size matrices plus
Θ(N2) scalar addition so
 Example:
Do on the board the example on the right. Notice that the answers are
the same for either order of parenthesizing but that the numbers of
multiplications are different.
Example:
Do on the board the example on the right. Notice that the answers are
the same for either order of parenthesizing but that the numbers of
multiplications are different.
 The diagram on the right illustrates the way dynamic program generates
the elements of N.
The diagram on the right illustrates the way dynamic program generates
the elements of N.