Operating Systems
================ Start Lecture #12 ================
Definition: A state is safe
if there is an ordering of the processes such that: if the
processes are run in this order, they will all terminate (assuming
none exceeds its claim).
Recall the comparison made above between detecting deadlocks (with
multi-unit resources and the banker's algorithm
-
The deadlock detection algorithm given makes the most
optimistic assumption
about a running process: it will return all its resources and
terminate normally.
If we still find processes that remain blocked, they are
deadlocked.
-
In the bankers algorithm we make the most pessimistic
assumption about a running process: it immediately asks for all
the resources it can (details later on “can”).
If, even with such demanding processes, the resource manager can
assure that all process terminates, then we can assure that
deadlock is avoided.
In the definition of a safe state no assumption is made about the
running processes; that is, for a state to be safe termination must
occur no matter what the processes do (providing the all terminate and
to not exceed their claims).
Give an example of all four possibilities. A state that is
-
Safe and deadlocked--not possible.
-
Safe and not deadlocked--trivial (e.g., no arcs).
-
Not safe and deadlocked--easy (any deadlocked state).
-
Not safe and not deadlocked--interesting.
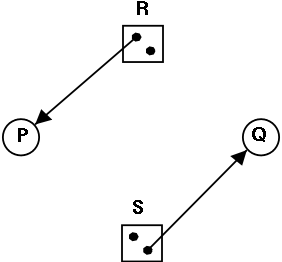 Is the figure on the right safe or not?
Is the figure on the right safe or not?
-
You can not tell until I give you the claims of the
process.
-
Please do not make the unfortunately common exam mistake to give
an example involving safe states without giving the claims.
-
For the figure on the right, if the claims are:
P: 1 unit of R and 2 units of S (written (1,2))
Q: 2 units of R and 1 units of S (written (2,1))
the state is NOT safe.
-
But if the claims are instead:
P: 2 units of R and 1 units of S (written (2,1))
Q: 1 unit of R and 2 units of S (written (1,2))
the state IS safe.
-
Explain why this is so.
A manager can determine if a state is safe.
-
Since the manager know all the claims, it can determine the maximum
amount of additional resources each process can request.
-
The manager knows how many units of each resource it has left.
The manager then follows the following procedure, which is part of
Banker's Algorithms discovered by Dijkstra, to
determine if the state is safe.
- If there are no processes remaining, the state is
safe.
- Seek a process P whose max additional requests is less than
what remains (for each resource type).
- If no such process can be found, then the state is
not safe.
- The banker (manager) knows that if it refuses all requests
excepts those from P, then it will be able to satisfy all
of P's requests. Why?
Ans: Look at how P was chosen.
- The banker now pretends that P has terminated (since the banker
knows that it can guarantee this will happen). Hence the banker
pretends that all of P's currently held resources are returned. This
makes the banker richer and hence perhaps a process that was not
eligible to be chosen as P previously, can now be chosen.
- Repeat these steps.
Example 1
A safe state with 22 units of one resource
| process | claim | current | max need |
|---|
| X | 3 | 1 | 2 |
| Y | 11 | 5 | 6 |
| Z | 19 | 10 | 9 |
| Total | 16 |
| Available | 6 |
- One resource type R with 22 unit
- Three processes X, Y, and Z with claims 3, 11, and 19 respectively.
- Currently the processes have 1, 5, and 10 units respectively.
- Hence the manager currently has 6 units left.
- Also note that the max additional needs for processes are 2, 6, 9
- So the manager cannot assure (with its current
remaining supply of 6 units) that Z can terminate. But that is
not the question.
- This state is safe
- Use 2 units to satisfy X; now the manager has 7 units.
- Use 6 units to satisfy Y; now the manager has 12 units.
- Use 9 units to satisfy Z; done!
Example 2
A unsafe state with 22 units of one resource
| process | claim | current | max need |
|---|
| X | 3 | 1 | 2 |
| Y | 11 | 5 | 6 |
| Z | 19 | 12 | 7 |
| Total | 18 |
| Available | 4 |
Start with example 1 and assume that Z now requests 2 units and we
grant them.
- Currently the processes have 1, 5, and 12 units respectively.
- The manager has 4 units.
- The max additional needs are 2, 6, and 7.
- This state is unsafe
- Use 2 unit to satisfy X; now the manager has 5 units.
- Y needs 6 and Z needs 7 so we can't guarantee satisfying either
- Note that we were able to find a process that can terminate (X)
but then we were stuck. So it is not enough to find one process.
We must find a sequence of all the processes.
Remark: An unsafe state is not necessarily
a deadlocked state. Indeed, if one gets lucky all processes may
terminate successfully. A safe state means that the manager can
guarantee that no deadlock will occur.
3.5.3: The Banker's Algorithm (Dijkstra) for a Single Resource
The algorithm is simple: Stay in safe states. Initially, we
assume all the processes are present before execution begins and that
all claims are given before execution begins.
We will relax these assumptions very soon.
-
Before execution begins, check that the system is safe.
That is, check that no process claims more than the manager has).
If not, then the offending process is trying to claim more of
some resource than exist in
the system has and hence cannot be guaranteed to complete even if
run by itself.
You might say that it can become deadlocked all by itself.
-
When the manager receives a request, it pretends to grant it and
checks if the resulting state is safe. If it is safe the request is
granted, if not the process is blocked.
-
When a resource is returned, the manager (politely thanks the
process and then) checks to see if “the first” pending
requests can be granted (i.e., if the result would now be
safe). If so the request is granted. The manager checks to see if
the next pending request can be granted, etc..
Homework: 13.
3.5.4: The Banker's Algorithm for Multiple Resources
At a high level the algorithm is identical: Stay in safe states.
-
What is a safe state?
-
The same definition (if processes are run in a certain order they
will all terminate).
-
Checking for safety is the same idea as above. The difference is
that to tell if there enough free resources for a processes to
terminate, the manager must check that for all
resources, the number of free units is at least equal to the max
additional need of the process.
Limitations of the banker's algorithm
-
Often users don't know the maximum requests a process will make.
They can estimate conservatively (i.e., use big numbers for the claim)
but then the manager becomes very conservative.
-
New processes arriving cause a problem (but not so bad as
Tanenbaum suggests).
-
The process's claim must be less than the total number of
units of the resource in the system. If not, the process is not
accepted by the manager.
-
Since the state without the new process is safe, so is the
state with the new process! Just use the order you had originally
and put the new process at the end.
-
Insuring fairness (starvation freedom) needs a little more
work, but isn't too hard either (once an hour stop taking new
processes until all current processes finish).
-
A resource becoming unavailable (e.g., a tape drive breaking), can
result in an unsafe state.
Homework: 21, 27, and 20. There is an interesting
typo in 20: A has claimed 3 units of resource 5,
but there are only 2 units in the entire system.
Change the problem by having B both claim and be allocated 1 unit of
resource 5.
3.7: Other Issues
3.7.1: Two-phase locking
This is covered (MUCH better) in a database text. We will skip it.
3.7.2: Non-resource deadlocks
You can get deadlock from semaphores as well as resources. This is
trivial. Semaphores can be considered resources. P(S) is request S
and V(S) is release S. The manager is the module implementing P and
V. When the manager returns from P(S), it has granted the resource S.
3.7.3: Starvation
As usual FCFS is a good cure. Often this is done by priority aging
and picking the highest priority process to get the resource. Also
can periodically stop accepting new processes until all old ones
get their resources.
3.8: Research on Deadlocks
Skipped.
3.9: Summary
Read.
 Is the figure on the right safe or not?
Is the figure on the right safe or not?
 Is the figure on the right safe or not?
Is the figure on the right safe or not?