Operating System
================ Start Lecture #11 ================
4.4: Page Replacement Algorithms (PRAs)
These are solutions to the replacement question.
Good solutions take advantage of locality.
- Temporal locality: If a word is referenced now,
it is likely to be referenced in the near future.
- This argues for caching referenced words,
i.e. keeping the referenced word near the processor for a while.
- Spatial locality: If a word is referenced now,
nearby words are likely to be referenced in the near future.
- This argues for prefetching words around the currently
referenced word.
- These are lumped together into locality: If any
word in a page is referenced, each word in the page is ``likely'' to
be referenced.
- So it is good to bring in the entire page on a miss and to
keep the page in memory for a while.
- When programs begin there is no history so nothing to base
locality on. At this point the paging system is said to be undergoing
a ``cold start''.
- Programs exhibit ``phase changes'', when the set of pages referenced
changes abruptly (similar to a cold start). At the point of a phase
change, many page faults occur because locality is poor.
Pages belonging to processes that have terminated are of course
perfect choices for victims.
Pages belonging to processes that have been blocked for a long time
are good choices as well.
Random PRA
A lower bound on performance. Any decent scheme should do better.
4.4.1: The optimal page replacement algorithm (opt PRA) (aka
Belady's min PRA)
Replace the page whose next
reference will be furthest in the future.
- Also called Belady's min algorithm.
- Provably optimal. That is, generates the fewest number of page
faults.
- Unimplementable: Requires predicting the future.
- Good upper bound on performance.
4.4.2: The not recently used (NRU) PRA
Divide the frames into four classes and make a random selection from
the lowest nonempty class.
- Not referenced, not modified
- Not referenced, modified
- Referenced, not modified
- Referenced, modified
Assumes that in each PTE there are two extra flags R (sometimes called
U, for used) and M (often called D, for dirty).
Also assumes that a page in a lower priority class is cheaper to evict.
- If not referenced, probably will not referenced again soon and
hence is a good candidate for eviction.
- If not modified, do not have to write it out so the cost of the
eviction is lower.
- When a page is brought in, OS resets R and M (i.e. R=M=0)
- On a read, hardware sets R.
- On a write, hardware sets R and M.
We again have the prisoner problem, we do a good job of making little
ones out of big ones, but not the reverse. Need more resets.
Every k clock ticks, reset all R bits
- Why not reset M?
Answer: Must have M accurate to know if victim needs to be written back
- Could have two M bits one accurate and one reset, but I don't know
of any system (or proposal) that does so.
What if the hardware doesn't set these bits?
- OS can use tricks
- When the bits are reset, make the PTE indicate the page is not
resident (i.e. lie). On the page fault, set the appropriate bit(s).
4.4.3: FIFO PRA
Simple but poor since usage of the page is ignored.
Belady's Anomaly: Can have more frames yet generate
more faults.
Example given later.
4.4.4: Second chance PRA
Similar to the FIFO PRA but when time choosing a victim, if the page
at the head of the queue has been referenced (R bit set), don't evict
it.
Instead reset R and move the page to the rear of the queue (so it
looks new).
The page is being a second chance.
What if all frames have been referenced?
Becomes the same as fifo (but takes longer).
Might want to turn off the R bit more often (say every k clock ticks).
4.4.5: Clock PRA
Same algorithm as 2nd chance, but a better (and I would say obvious)
implementation: Use a circular list.
Do an example.
LIFO PRA
This is terrible! Why?
Ans: All but the last frame are frozen once loaded so you can replace
only one frame. This is especially bad after a phase shift in the
program when it is using all new pages.
4.4.6:Least Recently Used (LRU) PRA
When a page fault occurs, choose as victim that page that has been
unused for the longest time, i.e. that has been least recently used.
LRU is definitely
- Implementable: The past is knowable.
- Good: Simulation studies have shown this.
- Difficult. Essentially need to either:
- Keep a time stamp in each PTE, updated on each reference
and scan all the PTEs when choosing a victim to find the PTE
with the oldest timestamp.
- Keep the PTEs in a linked list in usage order, which means
on each reference moving the PTE to the end of the list
Homework: 29, 23
A hardware cutsie in Tanenbaum
- For n pages, keep an nxn bit matrix.
- On a reference to page i, set row i to all 1s and col i to all 0s
-
At any time the 1 bits in the rows are ordered by inclusion. I.e. one
row's 1s are a subset of another row's 1s, which is a subset of a
third. (Tanenbaum forgets to mention this.)
-
So the row with the fewest 1s is a subset of all the others and is
hence least recently used
- Cute, but still impractical.
4.4.7: Simulating (Approximating) LRU in Software
The Not Frequently Used (NFU) PRA
- Include a counter in each PTE (and have R in each PTE).
- Set counter to zero when page is brought into memory.
- For each PTE, every k clock ticks.
- Add R to counter.
- Clear R.
- Choose as victim the PTE with lowest count.
| R | counter |
|---|
| 1 | 10000000 |
|
| 0 | 01000000 |
|
| 1 | 10100000 |
|
| 1 | 11010000 |
|
| 0 | 01101000 |
|
| 0 | 00110100 |
|
| 1 | 10011010 |
|
| 1 | 11001101 |
|
| 0 | 01100110 |
|
The Aging PRA
NFU doesn't distinguish between old references and recent ones. The
following modification does distinguish.
- Include a counter in each PTE (and have R in each PTE).
- Set counter to zero when page is brought into memory.
- For each PTE, every k clock ticks.
- Shift counter right one bit.
- Insert R as new high order bit (HOB).
- Clear R.
- Choose as victim the PTE with lowest count.
Homework: 25, 34
4.4.8: The Working Set Page Replacement Problem (Peter Denning)
The working set policy (Peter Denning)
The goal is to specify which pages a given process needs to have
memory resident in order for the give process to run without too many
page faults.
- But this is impossible since it requires predicting the future.
- So we make the assumption that the immediate future is well
approximated by the immediate past.
- Measure time in units of memory references, so t=1045 means the time
when the 1045th memory reference is issued.
- In fact we measure time separately
for each process, so t=1045 really means the time when this process
made its 1045th memory reference.
- W(t,&omega) is the set of pages referenced (by the given process) from
time t-ω to time t.
- That is, W(t,ω) is the set pages referenced during
the window of size ω ending at time t.
- That is, W(t,ω) is the set of pages referenced by the last
ω memory references ending at reference t.
- W(t,ω) is called the working set at time t
(with window ω).
- Does this Netscape support the ω notation to give the Greek letter?
- w(t,ω) is the size of the set W(t,ω), i.e. is the
number of pages referenced in the window.
The idea of the working set policy is to ensure that each process
keeps its working set in memory.
- Allocate w(t,ω) frames to each process.
This number differs for each process and changes with time.
- On a fault, one replaces a page not in the working set. But it is
not easy to find such a page quickly.
- Indeed determining W(t,ω) is difficult.
- We will see that the working set algorithm is essentially a
``global policy'' (defined below). I would actually prefer
covering the working set policy after defining local and global
policies but decided to follow Tannenbaum.
- If a process is suspended, it is often swapped out; the working
set then can be used to say which pages should be brought back
when the process is resumed.
Interesting questions include:
- What value should be used for ω?
Experiments have been done and ω is surprisingly robust (i.e.,
for a given system a fixed value works reasonably for a wide variety
of job mixes)
- How should we calculate W(t,ω)?
Hard so do exactly so ...
... Various approximations to the working set, have been devised.
We will study three: using virtual time instead of memory references
(immediately below),
WSClock (section 4.4.9), and Page Fault Frequency (section 4.6).
Using virtual time
Approximate the working set as those pages referenced during the
last m milliseconds.
Then clear the reference bit every m milliseconds and set it on every
reference.
Note that the time is measured only while this process is running.
That is why it is called virtual time.
So now to choose a victim, we need to find a page with the R bit
clear.
Similar to NRU.
4.4.9: The WSClock Page Replacement Algorithm
- Use the aging algorithm above to maintain a counter for
each PTE and declare a page whose counter is above a certain threshold
to be part of the working set.
- Apply the clock algorithm globally (i.e. to all pages) but
refuse to page out any page in a working set.
The resulting algorithm is called wsclock.
- What if we find there are no pages we can page out?
Simple answer: Pick some page (almost at random).
Another answer: Reduce the multiprogramming level
(explained in 4.6 below).
4.4.10: Summary of Page Replacement Algorithms
| Algorithm | Comment
|
|---|
| Random | Poor, used for comparison
|
| Optimal | Unimplementable, use for comparison
|
| LIFO | Horrible, useless
|
| NRU | Crude
|
| FIFO | Not good ignores frequency of use
|
| Second Chance | Improvement over FIFO
|
| Clock | Better (natural) implementation of Second Chance
|
| LRU | Great but impractical
|
| NFU | Crude LRU approximation
|
| Aging | Better LRU approximation
|
| Working Set | Good, but expensive
|
| WSClock | Good approximation to working set
|
4.5: Modeling Paging Algorithms
4.5.1: Belady's anomaly
Consider a system that has no pages loaded and that uses the FIFO
PRU.
Consider the following ``reference string'' (sequences of pages referenced).
0 1 2 3 0 1 4 0 1 2 3 4
If we have 3 frames this generates 9 page faults (do it).
If we have 4 frames this generates 10 page faults (do it).
Theory has been developed and certain PRA (so called ``stack
algorithms'') cannot suffer this anomaly for any reference string.
FIFO is clearly not a stack algorithm. LRU is. Tannenbaum has a few
details, but we are skipping it.
Repeat the above calculations for LRU.
4.6: Design issues for (demand) Paging Systems
4.6.1: Local vs Global Allocation Policies
A local PRA is one is which a victim page is chosen
among the pages of the same process that requires a new page. That is
the number of pages for each process is fixed. So LRU means the page
least recently used by this process.
- Of course we can't have a purely local policy, why?
Answer: A new process has no pages and even if we didn't apply this for
the first page loaded, the process would remain with only one page.
- Perhaps wait until a process has been running a while or give
the process an initial allocation based on the size of the executable.
- A global policy is one in which the choice of
victim is made among all pages of all processes.
If we apply global LRU indiscriminately with some sort of RR processor
scheduling policy, and memory is somewhat over-committed, then by the
time we get around to a process, all the others have run and have
probably paged out this process.
If this happens each process will need to page fault at a high
rate; this is called thrashing.
It is therefore important to get a good
idea of how many pages a process needs, so that we can balance the
local and global desires. The working set W(t,ω) is good for
this.
An approximation to the working set policy that is useful for
determining how many frames a process needs (but not which pages)
is the Page Fault Frequency (PFF) algorithm.
- For each process keep track of the page fault frequency, which
is the number of faults divided by the number of references.
- Actually, must use a window or a weighted calculation since
you are really interested in the recent page fault frequency.
- If the PFF is too high, allocate more frames to this process.
Either
- Raise its number of frames and use a local policy; or
- Bar its frames from eviction (for a while) and use a
global policy.
- What if there are not enough frames?
Answer: Reduce the MPL (see next section).
As mentioned above a question arises what to do if the sum of the
working set sizes exceeds the amount of physical memory available.
This question is similar to the final point about PFF and brings us to
consider controlling the load (or memory pressure).
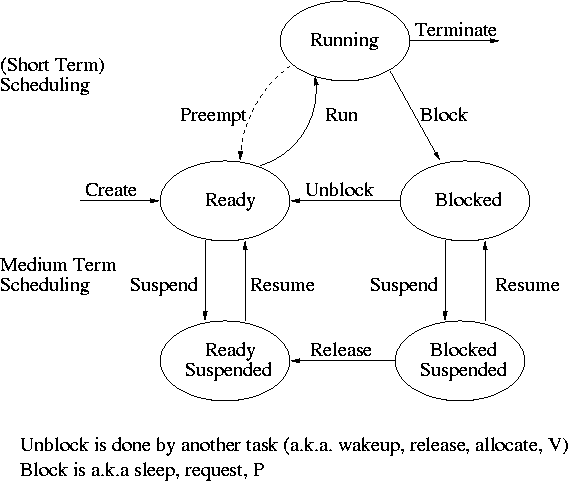
4.6.2: Load Control
To reduce the overall memory pressure, we must reduce the
multiprogramming level (or install more memory while the system is
running, which is hardly practical). That is, we have a
connection between memory management and process management. This is
the suspend/resume arcs we saw way back when.

