Operating System

Hardware assist (test and set)

The word atomically means that the two actions performed by TAS(x) (testing, i.e., returning the old value of x and setting , i.e., assigning true to x) are inseparable. Specifically it is not possible for two concurrent TAS(x) operations to both return false (unless there is also another concurrent statement that sets x to false).

With TAS available implementing a critical section for any number of processes is trivial.

loop forever {
    while (TAS(s)) {}   ENTRY
    CS
    s<--false           EXIT
    NCS

2.3.4: Sleep and Wakeup

Remark: Tanenbaum does both busy waiting (as above) and blocking (process switching) solutions. We will only do busy waiting, which is easier. Sleep and Wakeup are the simplest blocking primitives. Sleep voluntarily blocks the process and wakeup unblocks a sleeping process. We will not cover these.

Homework: Explain the difference between busy waiting and blocking.

2.3.5: Semaphores

Remark: Tannenbaum use the term semaphore only for blocking solutions. I will use the term for our busy waiting solutions. Others call our solutions spin locks.

P and V and Semaphores

The entry code is often called P and the exit code V. Thus the critical section problem is to write P and V so that

loop forever
    P
    critical-section
    V
    non-critical-section

1. Mutual exclusion.
2. No speed assumptions.
3. No blocking by processes in NCS.
4. Forward progress (my weakened version of Tanenbaum's last condition).

Note that I use indenting carefully and hence do not need (and sometimes omit) the braces {} used in languages like C or java.

A binary semaphore abstracts the TAS solution we gave for the critical section problem.

• A binary semaphore S takes on two possible values ``open'' and ``closed''.
• Two operations are supported
• P(S) is

      while (S=closed) {}
      S<--closed     <== This is NOT the body of the while
  

  where finding S=open and setting S<--closed is atomic
• That is, wait until the gate is open, then run through and atomically close the gate
• Said another way, it is not possible for two processes doing P(S) simultaneously to both see S=open (unless a V(S) is also simultaneous with both of them).
• V(S) is simply S<--open

The above code is not real, i.e., it is not an implementation of P. It is, instead, a definition of the effect P is to have.

To repeat: for any number of processes, the critical section problem can be solved by

loop forever
    P(S)
    CS
    V(S)
    NCS

The only specific solution we have seen for an arbitrary number of processes is the one just above with P(S) implemented via test and set.

Remark: Peterson's solution requires each process to know its processor number. The TAS soluton does not. Moreover the definition of P and V does not permit use of the processor number. Thus, strictly speaking Peterson did not provide an implementation of P and V. He did solve the critical section problem.

To solve other coordination problems we want to extend binary semaphores.

• With binary semaphores, two consecutive Vs do not permit two subsequent Ps to succeed (the gate cannot be doubly opened).
• We might want to limit the number of processes in the section to 3 or 4, not always just 1.

Both of the shortcomings can be overcome by not restricting ourselves to a binary variable, but instead define a generalized or counting semaphore.

• A counting semaphore S takes on non-negative integer values
• Two operations are supported
• P(S) is

      while (S=0) {}
      S--
  

  where finding S>0 and decrementing S is atomic
• That is, wait until the gate is open (positive), then run through and atomically close the gate one unit
• Another way to describe this atomicity is to say that it is not possible for the decrement to occur when S=0 and it is also not possible for two processes executing P(S) simultaneously to both see the same necessarily (positive) value of S unless a V(S) is also simultaneous.
• V(S) is simply S++

These counting semaphores can solve what I call the semi-critical-section problem, where you premit up to k processes in the section. When k=1 we have the original critical-section problem.

initially S=k

loop forever
    P(S)
    SCS   <== semi-critical-section
    V(S)
    NCS

Producer-consumer problem

• Two classes of processes
  • Producers, which produce times and insert them into a buffer.
  • Consumers, which remove items and consume them.
• What if the producer encounters a full buffer?
  Answer: It waits for the buffer to become non-full.
• What if the consumer encounters an empty buffer?
  Answer: It waits for the buffer to become non-empty.
• Also called the bounded buffer problem.
  • Another example of active entities being replaced by a data structure when viewed at a lower level (Finkel's level principle).

Initially e=k, f=0 (counting semaphore); b=open (binary semaphore)

Producer                         Consumer

loop forever                     loop forever
    produce-item                     P(f)
    P(e)                             P(b); take item from buf; V(b)
    P(b); add item to buf; V(b)      V(e)
    V(f)                             consume-item

• k is the size of the buffer
• e represents the number of empty buffer slots
• f represents the number of full buffer slots
• We assume the buffer itself is only serially accessible. That is, only one operation at a time.
  • This explains the P(b) V(b) around buffer operations
  • I use ; and put three statements on one line to suggest that a buffer insertion or removal is viewed as one atomic operation.
  • Of course this writing style is only a convention, the enforcement of atomicity is done by the P/V.
• The P(e), V(f) motif is used to force ``bounded alternation''. If k=1 it gives strict alternation.

2.3.6: Mutexes

My Terminology

	Busy wait	block/switch
critical	(binary) semaphore	(binary) semaphore
semi-critical	counting semaphore	counting semaphore

Tanenbaum's Terminology

	Busy wait	block/switch
critical	enter/leave region	mutex
semi-critical	no name	semaphore

2.3.7: Monitors

2.3..8: Message Passing

2.4: Classical IPC Problems

2.4.1: The Dining Philosophers Problem

A classical problem from Dijkstra

• 5 philosophers sitting at a round table
• Each has a plate of spaghetti
• There is a fork between each two
• Need two forks to eat

• The obvious solution (pick up right; pick up left) deadlocks.
• Big lock around everything serializes.
• Good code in the book.

The purpose of mentioning the Dining Philosophers problem without giving the solution is to give a feel of what coordination problems are like. The book gives others as well. We are skipping these (again this material would be covered in a sequel course). If you are interested look, for example, here.

Homework: 31 and 32 (these have short answers but are not easy). Note that the problem refers to fig. 2-20, which is incorrect. It should be fig 2-33, as noticed by Liang Chen.

2.4.2: The Readers and Writers Problem

• Two classes of processes.
  • Readers, which can work concurrently.
  • Writers, which need exclusive access.
• Must prevent 2 writers from being concurrent.
• Must prevent a reader and a writer from being concurrent.
• Must permit readers to be concurrent when no writer is active.
• Perhaps want fairness (e.g., freedom from starvation).
• Variants
  1. Writer-priority readers/writers.
  2. Reader-priority readers/writers.

Quite useful in multiprocessor operating systems and database systems. The ``easy way out'' is to treat all processes as writers in which case the problem reduces to mutual exclusion (P and V). The disadvantage of the easy way out is that you give up reader concurrency. Again for more information see the web page referenced above.

2.4.3: The Sleeping Barber Problem

2.5: Process Scheduling

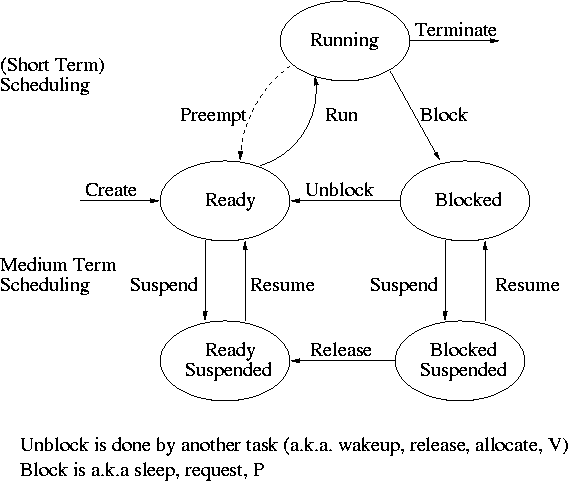
Scheduling processes on the processor is often called ``process scheduling'' or simply ``scheduling''.

The objectives of a good scheduling policy include

• Fairness.
• Efficiency.
• Low response time (important for interactive jobs).
• Low turnaround time (important for batch jobs).
• High throughput [the above are from Tanenbaum].
• More ``important'' processes are favored.
• Interactive processes are favored.
• Repeatability. Dartmouth (DTSS) ``wasted cycles'' and limited logins for repeatability.
• Fair across projects.
  • ``Cheating'' in unix by using multiple processes.
  • TOPS-10.
  • Fair share research project.
• Degrade gracefully under load.

Recall the basic diagram describing process states

For now we are discussing short-term scheduling, i.e., the arcs connecting running <--> ready.

Medium term scheduling is discussed later.

Preemption

It is important to distinguish preemptive from non-preemptive scheduling algorithms.

• Preemption means the operating system moves a process from running to ready without the process requesting it.
• Without preemption, the system implements ``run to completion (or yield or block)''.
• The ``preempt'' arc in the diagram.
• We do not consider yield (a solid arrow from running to ready).
• Preemption needs a clock interrupt (or equivalent).
• Preemption is needed to guarantee fairness.
• Found in all modern general purpose operating systems.
• Even non preemptive systems can be multiprogrammed (e.g., when processes block for I/O).