Basic Algorithms

Note: The following homework should have been assigned last time but wasn't so it is part of homework 9.

Homework: R-2.3

Remarks:

1. This is how you evaluate an arithmetic expression tree.
2. Evaluate some arithmetic expression trees.
3. When you write out the nodes in the order visited your get what is called either "reverse polish notation" or "polish notation".
4. If you do preorder traversal you get the other one.

Problem Set 2, Problem 1. Note that the height of a tree is the depth of a deepest node. Extend the height algorithm so that it returns in addition to the height the v.element() for some v that is of maximal depth.

2.3.3: Binary Trees

Recall that a binary tree is an ordered tree in which no node has more than two children. The left child is ordered before the right child.

The book adopts the convention that, unless otherwise mentioned, the term "binary tree" will mean "proper binary tree", i.e., all internal nodes have two children. This is a little convenient, but not a big deal. If you instead permitted non-proper binary trees, you would test if a left child existed before traversing it (similarly for right child.)

Will do binary preorder (first visit the node, then the left subtree, then the right subtree, binary postorder (left subtree, right subtree, node) and then inorder (left subtree, node, right subtree).

The Binary Tree ADT

We have three (accessor) methods in addition to the general tree methods.

1. leftChild(v): Return the (position of the) left child; signal an error if v is a leaf.
2. rightChild(v): Similar
3. sibling(v): Return the (unique) sibling of v; signal an error if v is the root (and hence has no sibling).

Remark: I will not hold you responsible for the proofs of the theorems.

Theorem: Let T be a binary tree having height h and n nodes. Then

1. The number of leaves in T is at least h+1 and at most 2^h.
2. The number of internal nodes in T is at least h and at most 2^h-1.
3. The number of nodes in T is at least 2h+1 and at most 2^h+1-1.
4. log(n+1)-1≤h≤(n-1)/2

Proof:

1. Induction on n the number of nodes in the tree.

   Base case n=1: Clearly true for all trees having only one node.

   Induction hypothesis: Assume true for all trees having at most k nodes.

   Main inductive step: prove the assertion for all trees having k+1 nodes. Let T be a tree with k nodes and let h be the height of T.

   Remove the root of T. The two subtrees produced each have no more than k nodes so satisfy the assertion. Since each has height at most h-1, each has at most 2^h-1 leaves. At least one of the subtrees has height exactly h-1 and hence has at least h leaves. Put the original tree back together.
   One subtree has at least h leaves, the other has at least 1, so the original tree has at least h+1. Each subtree has at most 2^h-1 leaves and the original root is not a leaf, so the original has at most 2^h leaves.
   

2. Same idea. Induction on the number of nodes. Clearly true if T has one node. Remove the root. At least one of the subtrees is height h-1 and hence has at least h-1 internal nodes. Each of the subtrees has height at most h-1 so has at most 2^h-1-1 internal nodes. Put the original tree back together. One subtree has at least h-1 internal nodes, the other has at least 1, so the original tree has at least h. Each subtree has at most 2^h-1-1 internal nodes and the original root is an internal node, so the original has at most 2(2^h-1)+1 = 2^h-1-1 internal nodes.
   
3. Add parts 1 and 2.
   
4. Take the log of part 3.

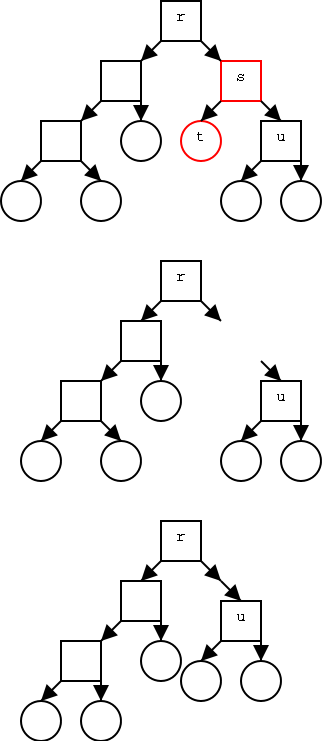
Theorem:In a binary tree T, the number of leaves is 1 more than the number of internal nodes.

Proof: Again induction on the number of nodes. Clearly true for one node. Assume true for trees with up to n nodes and let T be a tree with n+1 nodes. For example T is the top tree on the right.

1. Choose a leaf and its parent (which of course is internal). For example, the leaf t and parent s in red.
2. Remove the leaf and its parent (middle diagram)
3. Splice the tree back without the two nodes (bottom diagram).
4. Since S has n-1 nodes, S satisfies the assertion.
5. Note that T is just S + one leaf + one internal so also satisfies the assertion.

Alternate Proof (does not use the pictures):

1. Place two tokens on each internal node.
2. Push these tokens to the two children.
3. Notice that now all nodes but the root have one token; the root has none.
4. Hence 2*(number internal) = (number internal) + (number leaves) + 1
5. Done (slick!)

Corollary: A binary tree has an odd number of nodes.

Proof: #nodes = #leaves + #internal = 2(#internal)+1.

Preorder traversal of a binary tree

Algorithm binaryPreorder(T,v)
   Visit node v
   if T.isInternal(v) then
      binaryPreorder(T,T.leftChild(v))
      binaryPreorder(T,T.rightChild(v))

Algorithm binaryPretorder(T)
   binaryPreorder(T,T.root())

Postorder traversal of a binary tree

Algorithm binaryPostorder(T,v)
   if T.isInternal(v) then
      binaryPostorder(T,T.leftChild(v))
      binaryPostorder(T,T.rightChild(v))
   Visit node v

Algorithm binaryPosttorder(T)
   binaryPostorder(T,T.root())

Inorder traversal of a binary tree

Algorithm binaryInorder(T,v)
   if T.isInternal(v) then
      binaryInorder(T,T.leftChild(v))
   Visit node v
   if T.isInternal(v) then
      binaryInorder(T,T.rightChild(v))

Algorithm binaryIntorder(T)
   binaryPostorder(T,T.root())