Basic Algorithms

================ Start Lecture #6 ================

Problem Set #1, Problem 1.
The problem set will be officially assigned a little later, but the first problem in the set is C-2.2

2.2: Vectors, Lists, and Sequences

Unlike stacks and queues, the structures in this section support operations in the middle, not just at one or both ends.

2.2.1: Vectors

The rank of an element in a sequence is the number of elements before it. So if the sequence contains n elements, 0≤rank<n.

A vector storing n elements supports:

elemAtRank(r): Return the element with rank r. Report an error r<0 or r>n-1.
replaceAtRank(r,e): Replace the element at rank r with e and return it. Report an error r<0 or r>n-1.
insertAtRank(r,e): Insert e at rank r moving up existing elements with rank r and above. Report an error r<0 or r>n. If r=n, then we are inserting at the end (i.e., after all existing elements).
removeAtRank(r): Remove the element at rank r moving down existing elements with rank exceeding r. Report an error r<0 or r>n-1.
size().
isEmpty().

A Simple Array-Based Implementation

Use an array A and store the element with rank r in A[r].

Must shift elements when doing an insert or delete, which is expensive.
The code is below but does not include the error checks in the ADT
Limits the number of elements to N, the declared size of the array.
How can we remove the above limitation?
Ans: Use an extendable array.

Algorithm insertAtRank(r,e)
   for i = n-1, n-2, ..., r do
      A[i+1]←A[i]
   A[r]←e
   n←n+1

Algorithm removeAtRank(r)
   e←A[r]
   for i = r, r+1, ..., n-2 do
      A[i]←A[i+1]
   n←n-1
   return e

The worst-case time complexity of these two algorithms is Θ(n); the remaining algorithms are all Θ(1).

Homework: When does the worst case occur for insertAtRank(r,e) and removeAtRank(r)?

By using a circular array we can achieve Θ(1) time for insertAtRank(0,e) and removeAtRank(0). Indeed, that is the second problem of the first problem set.

Problem Set #1, Problem 2:
Part 1: C-2.5 from the book
Part 2: This implementation still has worst case complexity Θ(n). When does the worst case occur?

2.2.2: Lists

So far we have been considering what Knuth refers to as sequential allocation, when the next element is stored in the next location. Now we will be considering linked allocation, where each element refers explicitly to the next and/or preceding element(s).

Positions and Nodes

We think of each element as contained in a node, which is a placeholder that also contains references to the preceding and/or following node.

In C: struct node { int element; struct node *next; struct node *prev;}
In java: class Node { int element; Node next; Node prev;}

But in fact we don't want to expose Nodes to user's algorithms since this would freeze the possible implementation. Instead we define the idea (i.e., ADT) of a position in a list. The only method available to users is

element(): Return the element stored in this position.

The List ADT

Given the position ADT, we can now define the methods for the list ADT. The first methods only query a list; the last ones actually modify it.

-------------------------- read-only ------------------------
first(): Return the position of the first element; error if L is empty.
last(): Return the position of the last element; error if empty.
isFirst(p): Abbreviates p=first().
isLast(p): Abbreviates p=last().
before(p): Return the position preceding p; error if L is empty.
after(p): Return the position following p; error if empty.
size():
isEmpty():
-------------------------- updates ------------------------
replaceElement(p,e): Store e at p, return replaced element.
swapElements(p,q): Swap the elements at p and q.
insertBefore(p,e): Insert e in the position before p. The book says it is an error if p is the first position; that seems wrong, especially considering the next method. I explain what they likely meant below
insertFirst(e): Abbreviates insertBefore(first(),e).
insertAfter(p,e): Insert e in the position after p (analogous error comment).
insertLast(e): Abbreviates insertAfter(last(),e).
remove(p): Remove the element at position p.

A Linked List Implementation

Now when we are implementing a list we can certainly use the concept of nodes. In a singly linked list each node contains a next link that references the next node. A doubly linked list contains, in addition prev link that references the previous node.

Singly linked lists work well for stacks and queues, but do not perform well for general lists. Hence we use doubly linked lists

Homework: What is the worst case time complexity of insertBefore for a singly linked list implementation and when does it occur?

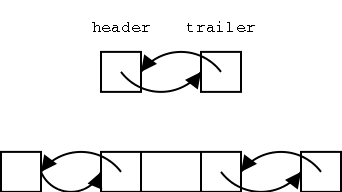
It is convenient to add two special nodes, a header and trailer. The header has just a next component, which links to the first node and the trailer has just a prev component, which links to the last node. For an empty list, the header and trailer link to each other and for a list of size 1, they both link to the only normal node.

In order to proceed from the top (empty) list to the bottom list (with one element), one would need to execute one of the insert methods. Ignoring the abbreviations, this means either insertBefore(p,e) or inserAfter(p,e). But this means that header and/or trailer must be an example of a position, one for which there is no element.

This observation explains the authors' comment above that insertBefore(p,e) cannot be applied if p is the first position. What they mean is that when we permit header and trailer to be positions, then we cannot insertBefore the first position, since that position is the header and the header has no prev. Similarly we cannot insertAfter the final position since that position is the trailer and the trailer has no next. Clearly not the authors' finest hour. Implementation Comment I have not done the implementation. It is probably easiest to have header and trailer have the same three components as a normal node, but have the prev of header and the next of trailer be some special value (say NULL) that can be tested for.

The insertAfter(p,e) Algorithm

The position p can be header, but cannot be trailer.

Algorithm insertAfter(p,e):
   If p is trailer signal an error
   Create a new node v
   v.element←e
   v.prev←p
   v.next←p.next
   (p.next).prev←v
   p.next← v
   return v

Do on the board the pointer updates for two cases: Adding a node after an ordinary node and after header. Note that they are the same. Indeed, that is what makes having the header and trailer so convenient.

Homework: Write pseudo code for insertBefore(p,e).

Note that insertAfter(header,e) and insertBefore(trailer,e) appear to be the only way to insert an element into an empty list. In particular, insertFirst(e) fails for an empty list since it performs insertBefore(first()) and first() generates an error for an empty list.

The remove(p) Algorithm

We cannot remove the header or trailer. Notice that removing the only element of a one-element list correctly produces an empty list.

Algorithm remove(p)
   if p is either header or trailer signal an error
   t←p.element
   (p.prev).next←p.next
   (p.next).prev←p.prev
   p.prev←NULL             // for security or debugging
   p.next←NULL
   return t

2.2.3: Sequences

Asymptotic complexity of the methods for both the array and list based implementations
Operation	Array	List
size, isEmpty	O(1)	O(1)
atRank, rankOf, elemAtRank	O(1)	O(n)
first, last, before, after	O(1)	O(1)
replaceElement, swapElements	O(1)	O(1)
replaceAtRank	O(1)	O(n)
insertAtRank, removeAtRank	O(n)	O(n)
insertFirst, insertLast	O(1)	O(1)
insertAfter, insertBefore	O(n)	O(1)
remove	O(n)	O(1)

Define a sequence ADT that includes all the methods of both vector and list ADTs as well as

atRank(r): Return the position of the element at rank r.
rankOf(p): Return the rank of the element at position p.

Sequences can be implemented as either circular arrays, as we did for vectors) or doubly linked lists, as we did for lists. Neither clearly dominates the other. Instead it depends on the relative frequency of the various operations. Circular arrays are faster for some and doubly liked lists are faster for others as the following table illustrates.

Iterators

An ADT for looping through a sequence one element at a time. It has two methods.

hasNext: Test whether there are elements left in the iterator
nextObject: Return and remove the next object in the iterator

When you create the iterator it has all the elements of the sequence. So a typical usage pattern would be

create iterator I for sequence S
while I hasNext
   process nextObject