1. So far the schemes presented so far have had two properties:
   1. Each job is stored contiguously in memory. That is, the job is contiguous in physical addresses.
   2. Each job cannot use more memory than exists in the system. That is, the virtual addresses space cannot exceed the physical address space.
   
   
2. Tanenbaum now attacks the second item. I wish to do both and start with the first.
   
   
3. Tanenbaum (and most of the world) uses the term ``paging'' to mean what I call demand paging. This is unfortunate as it mixes together two concepts.
   1. Paging (dicing the address space) to solve the placement problem and essentially eliminate external fragmentation.
   2. Demand fetching, to permit the total memory requirements of all loaded jobs to exceed the size of physical memory.
   
   
4. Tanenbaum (and most of the world) uses the term virtual memory as a synonym for demand paging. Again I consider this unfortunate.
   1. Demand paging is a fine term and is quite descriptive.
   2. Virtual memory ``should'' be used in contrast with physical memory to describe any virtual to physical address translation.

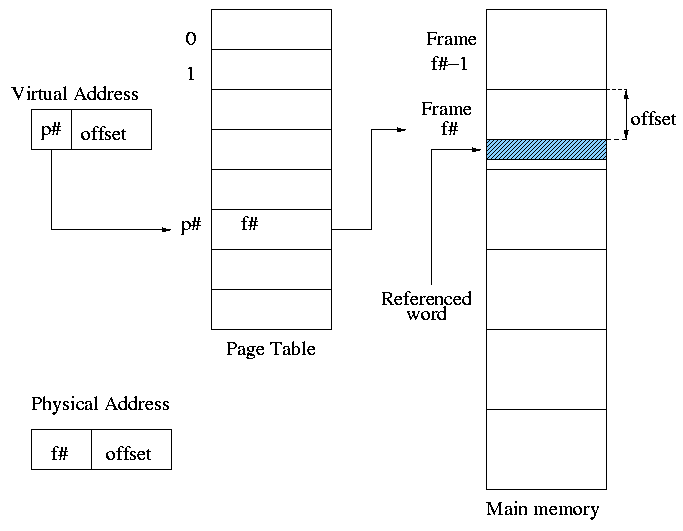
** (non-demand) Paging

Simplest scheme to remove the requirement of contiguous physical memory.

• Chop the program into fixed size pieces called pages (invisible to the programmer).
• Chop the real memory into fixed size pieces called page frames or simply frames.
• Size of a page (the page size) = size of a frame (the frame size).
• Sprinkle the pages into the frames.
• Keep a table (called the page table) having an entry for each page. The page table entry or PTE for page p contains the number of the frame f that contains page p.

Properties of (non-demand) paging.

• Entire job must be memory resident to run.
• No holes, i.e. no external fragmentation.
• If there are 50 frames available and the page size is 4KB than a job requiring <= 200KB will fit, even if the available frames are scattered over memory.
• Hence (non-demand) paging is useful.
• Introduces internal fragmentation approximately equal to 1/2 the page size for every process (really every segment).
• Can have a job unable to run due to insufficient memory and have some (but not enough) memory available. This is not called external fragmentation since it is not due to memory being fragmented.
• Eliminates the placement question. All pages are equally good since don't have external fragmentation.
• The replacement question remains.
• Since page boundaries occur at ``random'' points and can change from run to run (the page size can change with no effect on the program--other than performance), pages are not appropriate units of memory to use for protection and sharing. This is discussed further when we introduce segmentation.

Homework: 16.