================ Start Lecture #16
================
4.1.3: Modeling Multiprogramming
- Consider a job that is unable to compute (i.e., it is waiting for
I/O) a fraction p of the time.
- Then, with monoprogramming, the CPU utilization is 1-p.
- Note that p is often > .5 so CPU utilization is poor.
- But, if the probability that a
job is waiting for I/O is p and n jobs are in memory, then the
probability that all n are waiting for I/O is approximately p^n.
- So, with a multiprogramming level (MPL) of n,
the CPU utilization is approximately 1-p^n.
- If p=.5 and n=4, then 1-p^n = 15/16, which is much better than
1/2, which would occur for monoprogramming (n=1).
- This is a crude model, but it is correct that increasing MPL does
increase CPU utilization up to a point.
- The limitation is memory, which is why we discuss it here
instead of process management. That is, we must have many jobs
loaded at once, which means we must have enough memory for them.
There are other issues as well and we will discuss them.
- Some of the CPU utilization is time spent in the OS executing
context switches so the gains are not a great as the crude model predicts.
Homework: 1, 2 (typo in book; figure 4.21 seems
irrelevant).
4.1.4: Analysis of Multiprogramming System Performance
Skipped
4.1.5: Relocation and Protection
Relocation was discussed as part of linker lab and at the
beginning of this chapter.
When done dynamically, a simple method is to have a
base register whose value is added to every address by the
hardware.
Similarly a limit register is checked by the
hardware to be sure that the address (before the base register is
added) is not bigger than the size of the program.
The base and limit register are set by the OS when the job starts.
4.2: Swapping
Moving entire processes between disk and memory is called
swapping.
Multiprogramming with Variable Partitions
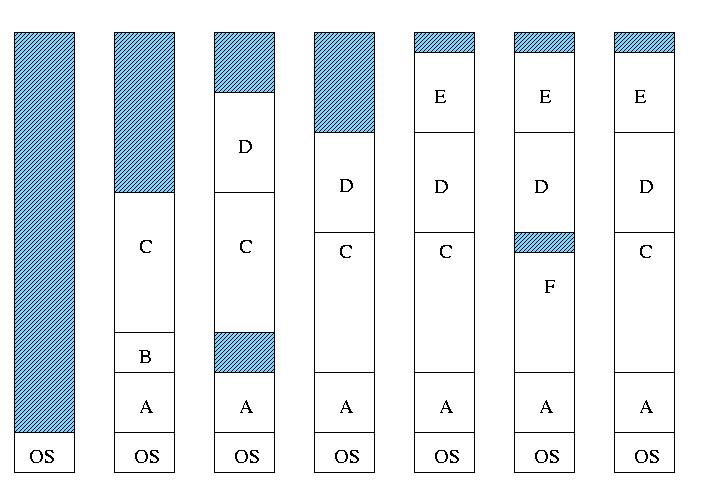 Both the number and size of the partitions change with time.
Both the number and size of the partitions change with time.
- IBM OS/MVT (multiprogramming with a varying number of tasks).
- Also early PDP-10 OS.
- Job still has only one segment (as with MFT) but now can be of any
size up to the size of the machine and can change with time.
- A single ready list.
- A job can move (might be swapped back in a different place).
- This is dynamic address translation (during run time).
- Must perform an addition on every memory reference (i.e. on every
address translation) to add the start address of the partition.
- Called a DAT (dynamic address translation) box by IBM.
- Eliminates internal fragmentation.
- Find a region the exact right size (leave a hole for the
remainder).
- Not quite true, can't get a piece with 10A755 bytes. Would
get say 10A760. But internal fragmentation is much
reduced compared to MFT. Indeed, we say that internal
fragmentation has been eliminated.
- Introduces external fragmentation, i.e., holes
outside any region.
- What do you do if no hole is big enough for the request?
- Can compactify
- Transition from bar 3 to bar 4 in diagram below.
- This is expensive.
- Not suitable for real time (MIT ping pong).
- Can swap out one process to bring in another, e.g., bars 5-6
and 6-7 in the diagram.
- There are more processes than holes. Why?
- Because next to a process there might be a process or a hole
but next to a hole there must be a process
- So can have ``runs'' of processes but not of holes
- If after a process equally likely to have a process or a hole,
you get about twice as many processes as holes.
- Base and limit registers are used.
- Storage keys not good since compactifying or moving would require
changing many keys.
- Storage keys might need a fine granularity to permit the
boundaries move by small amounts. Hence many keys would need to be
changed
Homework: 3
MVT Introduces the ``Placement Question''
That is, which hole (partition) should one choose?
- Best fit, worst fit, first fit, circular first fit, quick fit, Buddy
- Best fit doesn't waste big holes, but does leave slivers and
is expensive to run.
- Worst fit avoids slivers, but eliminates all big holes so a
big job will require compaction. Even more expensive than best
fit (best fit stops if it finds a perfect fit).
- Quick fit keeps lists of some common sizes (but has other
problems, see Tanenbaum).
- Buddy system
- Round request to next highest power of two (causes
internal fragmentation).
- Look in list of blocks this size (as with quick fit).
- If list empty, go higher and split into buddies.
- When returning coalesce with buddy.
- Do splitting and coalescing recursively, i.e. keep
coalescing until can't and keep splitting until successful.
- See Tanenbaum for more details (or an algorithms book).
- A current favorite is circular first fit, also know as next fit.
- Use the first hole that is big enough (first fit) but start
looking where you left off last time.
- Doesn't waste time constantly trying to use small holes that
have failed before, but does tend to use many of the big holes,
which can be a problem.
- Buddy comes with its own implementation. How about the others?
4.2.1: Memory Management with Bitmaps
Divide memory into blocks and associate a bit with each block, used
to indicate if the corresponding block is free or allocated. To find
a chunk of size N blocks need to find N consecutive bits
indicating a free block.
The only design question is how much memory does one bit represent.
- Big: Serious internal fragmentation.
- Small: Many bits to store and process.
4.2.2: Memory Management with Linked Lists
- Each item on list gives the length and starting location of the
corresponding region of memory and says whether it is a Hole or Process.
- The items on the list are not taken from the memory to be
used by processes.
- Keep in order of starting address.
- Merge adjacent holes
- Double linked
Memory Management using Boundary Tags
- Use the same memory for list items as for processes
- Don't need an entry in linked list for blocks in use, just
the avail blocks are linked.
- For the blocks currently in use, just need a hole/process bit at
each end and the length. Keep this in the block itself.
- See Knuth, The Art of Computer Programming vol 1.
Homework: 5.
MVT also introduces the ``Replacement Question''
That is, which victim should we swap out?
Note that this is an example of the suspend arc mentioned in process
scheduling.
We will study this question more when we discuss
demand paging in which case
we swap out part of a process.
Considerations in choosing a victim
- Cannot replace a job that is pinned,
i.e. whose memory is tied down. For example, if Direct Memory
Access (DMA) I/O is scheduled for this process, the job is pinned
until the DMA is complete.
- Victim selection is a medium term scheduling decision
- A job that has been in a wait state for a long time is a good
candidate.
- Often choose as a victim a job that has been in memory for a long
time.
- Another question is how long should it stay swapped out.
- For demand paging, where swaping out a page is not as drastic as
swapping out a job, choosing the victim is an important memory
management decision and we shall study several policies,
 Both the number and size of the partitions change with time.
Both the number and size of the partitions change with time.