======== START LECTURE #22
========
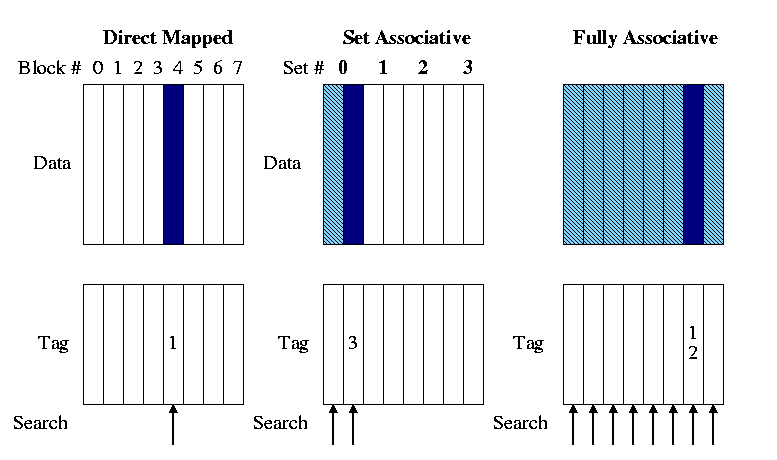
Most common for caches is an intermediate configuration called
set associative or n-way associative (e.g., 4-way
associative).
- n is typically 2, 4, or 8.
- If the cache has B blocks, we group them into B/n
sets each of size n. Memory block number K is
then stored in set K mod (B/n).
- Figure 7.15 has a bug. It indicates that the tag for memory
block 12 is 12 for all associativities. The figure below
corrects this.
- In the picture we are trying to store memory block 12 in each
of three caches.
- The light blue represents cache blocks in which the memory
block might have been stored.
- The dark blue is the cache block in which the memory block
is stored.
- The arrows show the blocks (i.e., tags) that must be
searched to look for memory block 12. Naturally the arrows
point to the blue blocks.
-
The picture shows 2-way set set associative. Do on the board
4-way set associative.
-
Determining the Set# and Tag.
- The Set# = (memory) block# mod #sets.
- The Tag = (memory) block# / #sets.
-
Ask in class.
- What is 8-way set associative in a cache with 8 blocks (i.e.,
the cache in the picture)?
- What is 1-way set associative?
-
Why is set associativity good? For example, why is 2-way set
associativity better than direct mapped?
-
Consider referencing two modest arrays (<< cache size) that
start at location 1MB and 2MB.
-
Both will contend for the same cache locations in a direct
mapped cache but will fit together in an n-way associative
cache with n>=2.

How do we find a memory block in an associative cache (with
block size 1 word)?
- Divide the memory block number by the number of sets to get
the index into the cache.
- Mod the memory block number by the number of sets to get the tag.
- Check all the tags in the set against the tag of the
memory block.
- If any tag matches, a hit has occurred and the
corresponding data entry contains the memory block.
- If no tag matches, a miss has occurred.
-
Why is set associativity bad?
Ans: It is a little slower due to the mux and AND gate.
-
Which block (in the set) should be replaced?
-
Random is sometimes used.
- But it is not used for paging!
- The number of blocks in a set is small, so the likely
difference in quality between the best and the worst is less.
- For caches, speed is crucial so have no time for
calculations, even for misses.
-
LRU is better, but not easy to do quickly.
-
If the cache is 2-way set associative, each set is of size
two and it is easy to find the lru block quickly.
How?
Ans: For each set keep a bit indicating which block in the set
was just referenced and the lru block is the other one.
-
If the cache is 4-way set associative, each set is of size
4. Consider these 4 blocks as two groups of 2. Use the
trick above to find the group most recently used and pick
the other group. Also use the trick within each group and
chose the block in the group not used last.
-
Sound great. We can do lru fast for any power of two using
a binary tree.
-
Wrong! The above is
not LRU it is just an approximation. Show this on the board.
-
Sizes
- How big is the cache? This means, what is the capacity or how
big is the blue?
Ans: 256 * 4 * 4B = 4KB.
- How many bits are in the cache?
- Answer
- The 32 address bits contain 8 bits of index and 2 bits
giving the byte offset.
- So the tag is 22 bits (more examples just below).
- Each block contains 1 valid bit, 22 tag bits and 32 data
bits, for a total of 55 bits.
- There are 1K blocks.
- So the total size is 55Kb (kilobits).
- What fraction of the bits are user data?
Ans: 4KB / 53Kb = 32Kb / 53Kb = 32/53.
Tag size and division of the address bits
We continue to assume a byte addressed machines with all references
to a 4-byte word (lw and sw).
The 2 LOBs are not used (they specify the byte within the word but
all our references are for a complete word). We show these two bits in
dark blue.
We continue to assume 32
bit addresses so there are 2**30 words in the address space.
Let's review various possible cache organizations and determine for
each how large is the tag and how the various address bits are used.
We will always use a 16KB cache. That is the size of the
data portion of the cache is 16KB = 4 kilowords =
2**12 words.
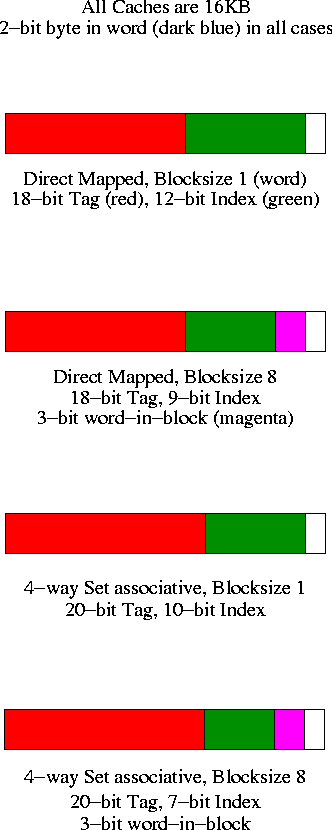
- Direct mapped, blocksize 1 (word).
- Since the blocksize is one word, there are 2**30 memory blocks
and all the address bits (except the uncolored 2 LOBs that specify
the byte
within the word) are used for the memory block number.
Specifically 30 bits are so used.
- The cache has 2**12 words, which is 2**12 blocks.
- So the low order 12 bits of the memory block number give the
index in the cache (the cache block number), shown in green.
- The remaining 18 (30-12) bits are the tag, shown in red.
- Direct mapped, blocksize 8
- Three bits of the address give the word within the 8-word
block. These are drawn in magenta.
- The remaining 27 HOBs of the
memory address give the memory block number.
- The cache has 2**12 words, which is 2**9 blocks.
- So the low order 9 bits of the memory block number gives the
index in the cache.
- The remaining 18 bits are the tag
- 4-way set associative, blocksize 1
- Blocksize is 1 so there are 2**30 memory blocks and 30 bits
are used for the memory block number.
- The cache has 2**12 blocks, which is 2**10 sets (each set has
4=2**2 blocks).
- So the low order 10 bits of the memory block number gives
the index in the cache.
- The remaining 20 bits are the tag.
- As the associativity grows, the tag gets bigger. Why?
Ans: Growing associativity reduces the number of sets into which a
block can be placed. This increases the number of memory blocks
eligible tobe placed in a given set. Hence more bits are needed
to see if the desired block is there.
- 4-way set associative, blocksize 8
- Three bits of the address give the word within the block.
- The remaining 27 HOBs of the
memory address give the memory block number.
- The cache has 2**12 words = 2**9 blocks = 2**7 sets.
- So the low order 7 bits of the memory block number gives
the index in the cache.
Homework: 7.39, 7.40
Improvement: Multilevel caches
Modern high end PCs and workstations all have at least two levels
of caches: A very fast, and hence not very big, first level (L1) cache
together with a larger but slower L2 cache.
When a miss occurs in L1, L2 is examined, and only if a miss occurs
there is main memory referenced.
So the average miss penalty for an L1 miss is
(L2 hit rate)*(L2 time) + (L2 miss rate)*(L2 time + memory time)
We are assuming L2 time is the same for an L2 hit or L2 miss. We are
also assuming that the access doesn't begin to go to memory until the
L2 miss has occurred.
Do an example
- Assume
- L1 I-cache miss rate 4%
- L1 D-cache miss rate 5%
- 40% of instructions reference data
- L2 miss rate 6%
- L2 time of 15ns
- Memory access time 100ns
- Base CPI of 2
- Clock rate 400MHz
- How many instructions per second does this machine execute
- How many instructions per second would this machine execute if
the L2 cache were eliminated.
- How many instructions per second would this machine execute if
both caches were eliminated.
- How many instructions per second would this machine execute if the
L2 cache had a 0% miss rate (L1 as originally specified).
- How many instructions per second would this machine execute if
both L1 caches had a 0% miss rate
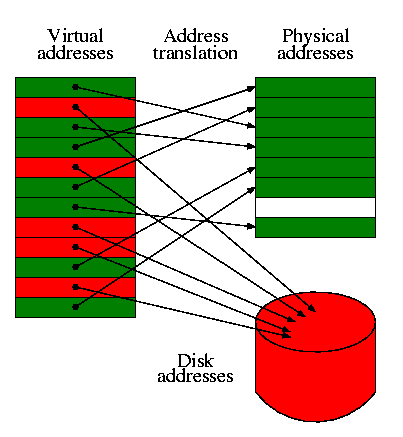
7.4: Virtual Memory
I realize this material was covered in operating systems class
(V22.0202). I am just reviewing it here. The goal is to show the
similarity to caching, which we just studied. Indeed, (the demand
part of) demand paging is caching: In demand paging the
memory serves as a cache for the disk, just as in caching the cache
serves as a cache for the memory.
The names used are different and there are other differences as well.
| Cache concept | Demand paging analogue |
|---|
| Memory block | Page |
| Cache block | Page Frame (frame) |
| Blocksize | Pagesize |
| Tag | None (table lookup) |
| Word in block | Page offset |
| Valid bit | Valid bit |
| Miss | Page fault |
| Hit | Not a page fault |
| Miss rate | Page fault rate |
| Hit rate | 1 - Page fault rate |
| Cache concept | Demand paging analogue |
|---|
| Placement question | Placement question |
| Replacement question | Replacement question |
| Associativity | None (fully associative) |
- For both caching and demand paging, the placement
question is trivial since the items are fixed size (no first-fit,
best-fit, buddy, etc).
- The replacement question is not trivial. (H&P
list this under the placement question, which I believe is in error).
Approximations to LRU are popular for both caching and demand
paging.
- The cost of a page fault vastly exceeds the cost of a cache miss
so it is worth while in paging to slow down hit processing to lower
the miss rate. Hence demand paging is fully associative and uses a
table to locate the frame in which the page is located.
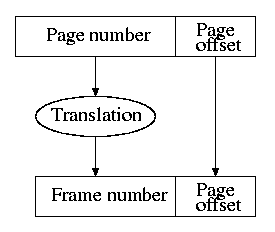
- The figures to the right are for demand paging. But they can be
interpreted for caching as well.
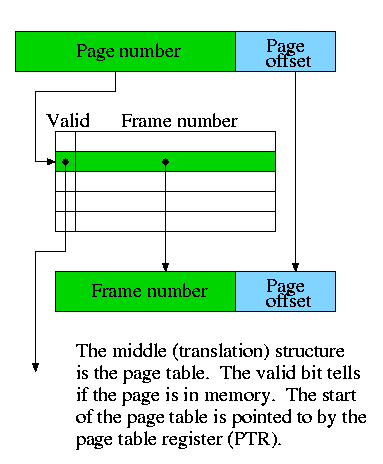
- The (virtual) page number is the memory block number
- The Page offset is the word-in-block
- The frame (physical page) number is the cache block number
(which is the index into the cache).
- Since demand paging uses full associativity, the tag is the
entire memory block number. Instead of checking every cache block
to see if the tags match, a (page) table is used.
Homework: 7.32
Write through vs. write back
Question: On a write hit should we write the new value through to
(memory/disk) or just keep it in the (cache/memory) and write it back
to (memory/disk) when the (cache-line/page) is replaced?
- Write through is simpler since write back requires two operations
at a single event.
- But write-back has fewer writes to (memory/disk) since multiple
writes to the (cache-line/page) may occur before the (cache-line/page)
is evicted.
- For caching the cost of writing through to memory is probably less
than 100 cycles so with a write buffer the cost of write through is
bearable and it does simplify the situation.
- For paging the cost of writing through to disk is on the order of
1,000,000 cycles. Since write-back has fewer writes to disk, it is used.
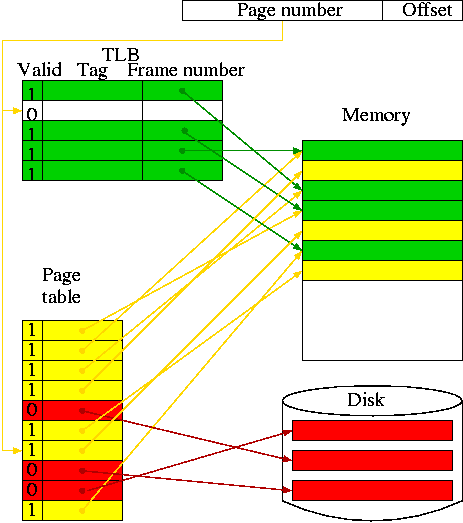
Translation Lookaside Buffer (TLB)
A TLB is a cache of the page table
- Needed because otherwise every memory reference in the program
would require two memory references, one to read the page table and
one to read the requested memory word.
- Typical TLB parameter values
- Size: hundreds of entries.
- Block size: 1 entry.
- Hit time: 1 cycle.
- Miss time: tens of cycles.
- Miss rate: Low (<= 2%).
- In the diagram on the right:
- The green path is the fastest (TLB hit).
- The red is the slowest (page fault).
- The yellow is in the middle (TLB miss, no page fault).
- Really the page table doesn't point to the disk block for an
invalid entry, but the effect is the same.
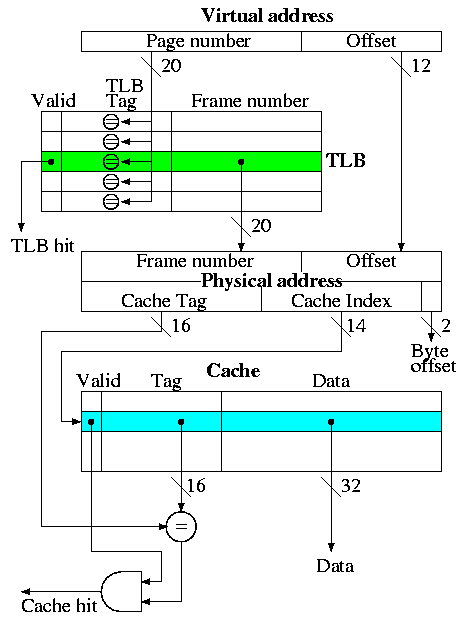
Putting it together: TLB + Cache
This is the decstation 3100
- Virtual address = 32 bits
- Physical address = 32 bits
- Fully associative TLB (naturally)
- Direct mapped cache
- Cache blocksize = one word
- Pagesize = 4KB = 2^12 bytes
- Cache size = 16K entries = 64KB
Actions taken
- The page number is searched in the fully associative TLB
- If a TLB hit occurs, the frame number from the TLB together with
the page offset gives the physical address. A TLB miss causes an
exception to reload the TLB from the page table, which the figure does
not show.
- The physical address is broken into a cache tag and cache index
(plus a two bit byte offset that is not used for word references).
- If the reference is a write, just do it without checking for a
cache hit (this is possible because the cache is so simple as we
discussed previously).
- For a read, if the tag located in the cache entry specified by the
index matches the tag in the physical address, the referenced word has
been found in the cache; i.e., we had a read hit.
- For a read miss, the cache entry specified by the index is fetched
from memory and the data returned to satisfy the request.
Hit/Miss possibilities
| TLB | Page | Cache | Remarks |
|---|
| hit | hit | hit |
Possible, but page table not checked on TLB hit, data from cache |
| hit | hit | miss |
Possible, but page table not checked, cache entry loaded from memory |
| hit | miss | hit |
Impossible, TLB references in-memory pages |
| hit | miss | miss |
Impossible, TLB references in-memory pages |
| miss | hit | hit |
Possible, TLB entry loaded from page table, data from cache |
| miss | hit | miss |
Possible, TLB entry loaded from page table, cache entry loaded from memory |
| miss | miss | hit |
Impossible, cache is a subset of memory |
| miss | miss | miss |
Possible, page fault brings in page, TLB entry loaded, cache loaded |
Homework: 7.31, 7.33
7.5: A Common Framework for Memory Hierarchies
Question 1: Where can/should the block be placed?
This question has three parts.
- In what slot are we able to place the block.
- For a direct mapped cache, there is only one choice.
- For an n-way associative cache, there are n choices.
- For a fully associative cache, any slot is permitted.
- The n-way case includes both the direct mapped and fully
associative cases.
- For a TLB any slot is permitted. That is, a TLB is a fully
associative cache of the page table.
- For paging any slot (i.e., frame) is permitted. That is,
paging uses a fully associative mapping (via a page table).
- For segmentation, any large enough slot (i.e., region) can be
used.
- If several possible slots are available, which one should
be used?
- I call this question the placement question.
- For caches, TLBs and paging, which use fixed size
slots, the question is trivial; any available slot is just fine.
- For segmentation, the question is interesting and there are
several algorithms, e.g., first fit, best fit, buddy, etc.
- If no possible slots are available, which victim should be chosen?
- I call this question the replacement question.
- For direct mapped caches, the question is trivial. Since the
block can only go in one slot, if you need to place the block and
the only possible slot is not available, it must be the victim.
- For all the other cases, n-way associative caches (n>1), TLBs
paging, and segmentation, the question is interesting and there
are several algorithms, e.g., LRU, Random, Belady min, FIFO, etc.
- See question 3, below.
Question 2: How is a block found?
| Associativity | Location method | Comparisons Required |
|---|
| Direct mapped | Index | 1 |
| Set Associative | Index the set, search among elements
| Degree of associativity |
| Full | Search all cache entries
| Number of cache blocks |
| Separate lookup table | 0 |
Typical sizes and costs
| Feature |
Typical values
for caches |
Typical values
for demand paging |
Typical values
for TLBs |
| Size |
8KB-8MB |
16MB-2GB |
256B-32KB |
| Block size |
16B-256B |
4KB-64KB |
4B-32B |
| Miss penalty in clocks |
10-100 |
1M-10M |
10-100 |
| Miss rate |
.1%-10% |
.000001-.0001% |
.01%-2% |
|
The difference in sizes and costs for demand paging vs. caching,
leads to different algorithms for finding the block.
Demand paging always uses the bottom row with a separate table (page
table) but caching never uses such a table.
- With page faults so expensive, misses must be reduced as much as
possible. Hence full associativity is used.
- With such a large associativity (fully associative with many
slots), hardware would be prohibitively expensive and software
searching too slow. Hence a page table is used with a TLB acting as a
cache.
- The large block size (called the page size) means that the extra table
is a small fraction of the space.
Question 3: Which block should be replaced?
This is called the replacement question and is much
studied in demand paging (remember back to 202).
- For demand paging, with miss costs so high and associativity so
large, the replacement policy is very important and some approximation
to LRU is used.
- For caching, even the miss time must be small so simple schemes
are used. For 2-way associativity, LRU is trivial. For higher
associativity (but associativity is never very high) crude
approximations to LRU may be used and sometimes even random
replacement is used.
Question 4: What happens on a write?
- Write-through
- Data written to both the cache and main memory (in general to
both levels of the hierarchy).
- Sometimes used for caching, never used for demand paging.
- Advantages
- Misses are simpler and cheaper (no copy back).
- Easier to implement, especially for block size 1, which we
did in class.
- For blocksize > 1, a write miss is more complicated since
the rest of the block now is invalid. Fetch the rest of the
block from memory (or mark those parts invalid by extra valid
bits--not covered in this course).
Homework: 7.41
- Write-back
- Data only written to the cache. The memory has stale data,
but becomes up to date when the cache block is subsequently
replaced in the cache.
- Only real choice for demand paging since writing to the lower
level of the memory hierarch (in this case disk) is so slow.
- Advantages
- Words can be written at cache speed not memory speed
- When blocksize > 1, writes to multiple words in the cache
block are only written once to memory (when the block is
replaced).
- Multiple writes to the same word in a short period are
written to memory only once.
- When blocksize > 1, the replacement can utilize a high
bandwidth transfer. That is, writing one 64-byte block is
faster than 16 writes of 4-bytes each.
Write miss policy (advanced)
- For demand paging, the case is pretty clear. Every
implementation I know of allocates frame for the page miss and
fetches the page from disk. That is it does both an
allocate and a fetch.
- For caching this is not always the case. Since there are two
optional actions there are four possibilities.
- Don't allocate and don't fetch: This is sometimes called
write around. It is done when the data is not expected to be
read before it will be evicted. For example, if you are
writing a matrix whose size is much larger than the cache.
- Don't allocate but do fetch: Impossible, where would you
put the fetched block?
- Do allocate, but don't fetch: Sometimes called
no-fetch-on-write. Also called SANF
(store-allocate-no-fetch). Requires multiple valid bits per
block since the just-written word is valid but the others are
not (since we updated the tag to correspond to the
just-written word).
- Do allocate and do fetch: The normal case we have been
using.








