Memory support for wider blocks

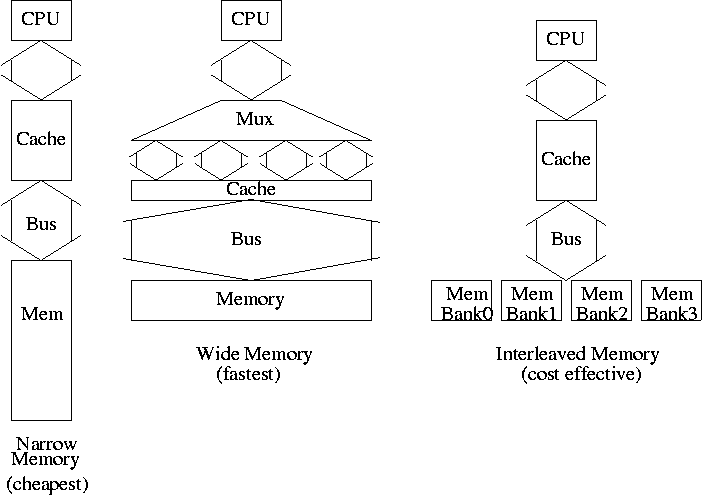
• Should memory be wide?
• Should the bus from the cache to the processor be wide?
• Assume
  1. 1 clock required to send the address. Only one address is needed per access for all designs.
  2. 15 clocks are required for each memory access (independent of width).
  3. 1 Clock/busload required to transfer data.
• How long does it take satisfy a read miss for the cache above and each of the three memory/bus systems.
• Narrow design (a) takes 65 clocks: 1 address transfer, 4 memory reads, 4 data transfers (do it on the board).
• Wide design (b) takes 17.
• Interleaved design (c) takes 20.
• Interleaving works great because in this case we are guaranteed to have sequential accesses.
• Imagine a design between (a) and (b) with a 2-word wide datapath.
  It takes 33 cycles and is more expensive to build than (c).

Homework: 7.11

7.3: Measuring and Improving Cache Performance

Performance example to do on the board (a dandy exam question).

• Assume
  • 5% I-cache miss.
  • 10% D-cache miss.
  • 1/3 of the instructions access data.
  • CPI = 4 if miss penalty is 0 (A 0 miss penalty is not realistic of course).
• What is CPI with miss penalty 12 (do it)?
• What is CPI if we upgrade to a double speed cpu+cache, but keep a single speed memory (i.e., a 24 clock miss penalty)?
  Do it on the board.
• How much faster is the ``double speed'' machine? It would be double speed if the miss penalty were 0 or if there was a 0% miss rate.

Homework: 7.15, 7.16

A lower base (i.e. miss-free) CPI makes stalls appear more expensive since waiting a fixed amount of time for the memory corresponds to losing more instructions if the CPI is lower.

A faster CPU (i.e., a faster clock) makes stalls appear more expensive since waiting a fixed amount of time for the memory corresponds to more cycles if the clock is faster (and hence more instructions since the base CPI is the same).

Another performance example.

• Assume
  1. I-cache miss rate 3%.
  2. D-cache miss rate 5%.
  3. 40% of instructions reference data.
  4. miss penalty of 50 cycles.
  5. Base CPI is 2.
• What is the CPI including the misses?
• How much slower is the machine when misses are taken into account?
• Redo the above if the I-miss penalty is reduced to 10 (D-miss still 50)
• With I-miss penalty back to 50, what is performance if CPU (and the caches) are 100 times faster

Remark: Larger caches have longer hit times.

Improvement: Associative Caches

Consider the following sad story. Jane has a cache that holds 1000 blocks and has a program that only references 4 (memory) blocks, namely 23, 1023, 123023, and 7023. In fact the references occur in order: 23, 1023, 123023, 7023, 23, 1023, 123023, 7023, 23, 1023, 123023, 7023, 23, 1023, 123023, 7023, etc. Referencing only 4 blocks and having room for 1000 in her cache, Jane expected an extremely high hit rate for her program. In fact, the hit rate was zero. She was so sad, she gave up her job as webmistress, went to medical school, and is now a brain surgeon at the mayo clinic in rochester MN.

So far We have studied only direct mapped caches, i.e. those for which the location in the cache is determined by the address. Since there is only one possible location in the cache for any block, to check for a hit we compare one tag with the HOBs of the addr.

The other extreme is fully associative.

• A memory block can be placed in any cache block.
• Since any memory block can be in any cache block, the cache index where the memory block is stored tells us nothing about which memory block is stored there. Hence the tag must be the entire address. Moreover, we don't know which cache block to check so we must check all cache blocks to see if we have a hit.
• The larger tag is a problem.
• The search is a disaster.
  • It could be done sequentially (one cache block at a time), but this is much too slow.
  • We could have a comparator with each tag and mux all the blocks to select the one that matches.
    • This is too big due to both the many comparators and the humongous mux.
    • However, it is exactly what is done when implementing translation lookaside buffers (TLBs), which are used with demand paging.
    • Are the TLB designers magicians?
      Ans: No. TLBs are small.
• An alternative is to have a table with one entry per MEMORY block giving the cache block number. This is too big and too slow for caches but is used for virtual memory (demand paging).