We must decide when the midterm will be. It must be graded and returned by tues 30 Oct. Thus it must be given by thurs 25 Oct. Also possible is tues 23 Oct.

End of Note

Fast Adders

1. We have done what is called a ripple carry adder.
   • The carry ``ripples'' from one bit to the next (LOB to HOB).
   • So the time required is proportional to the wordlength
   • Each carry can be computed with two levels of logic (any function can be so computed) hence the number of gate delays for an n bit adder is 2n.
     • For a 4-bit adder 8 gate delays are required.
     • For an 16-bit adder 32 gate delays are required.
     • For an 32-bit adder 64 gate delays are required.
     • For an 64-bit adder 128 gate delays are required.
2. What about doing the entire 32 (or 64) bit adder with 2 levels of logic?
   • Such a circuit clearly exists. Why?
     Ans: A two levels of logic circuit exists for any function.
   • But it would be very expensive: many gates and wires.
   • The big problem: When expressed with two levels of login, the AND and OR gates have high fan-in, i.e., they have a large number of inputs. It is not true that a 64-input AND takes the same time as a 2-input AND.
   • Unless you are doing full custom VLSI, you get a toolbox of primative functions (say 4 input NAND) and must build from that
3. There are faster adders, e.g. carry lookahead and carry save. We will study carry lookahead adders.

Carry Lookahead Adder (CLA)

This adder is much faster than the ripple adder we did before, especially for wide (i.e., many bit) addition.

• For each bit position we have two input bits, a and b (really should say ai and bi as I will do below).
• We can, in one gate delay, calculate two other bits called generate g and propagate p, defined as follows:
• The idea for propagate is that p is true if the current bit will propagate a carry from its input to its output.
• It is easy to see that p = (a OR b), i.e.
  if and only if (a OR b)
  then if there is a carry in
         then there is a carry out
• The idea for generate is that g is true if the current bit will generate a carry out (independent of the carry in).
• It is easy to see that g = (a AND b), i.e.
  if and only if (a AND b)
  then the must be a carry-out independent of the carry-in

To summarize, using a subscript i to represent the bit number,

    to generate  a carry:   gi = ai bi
    to propagate a carry:   pi = ai+bi

H&P give a plumbing analogue for generate and propagate.

Given the generates and propagates, we can calculate all the carries for a 4-bit addition (recall that c0=C_in is an input) as follows (this is the formula version of the plumbing):

c1 = g0 + p0 c0

c2 = g1 + p1 c1 = g1 + p1 g0 + p1 p0 c0

c3 = g2 + p2 c2 = g2 + p2 g1 + p2 p1 g0 + p2 p1 p0 c0

c4 = g3 + p3 c3 = g3 + p3 g2 + p3 p2 g1 + p3 p2 p1 g0 + p3 p2 p1 p0 c0

Thus we can calculate c1 ... c4 in just two additional gate delays (where we assume one gate can accept upto 5 inputs). Since we get gi and pi after one gate delay, the total delay for calculating all the carries is 3 (this includes c4=Carry-Out)

Each bit of the sum si can be calculated in 2 gate delays given ai, bi, and ci. Thus, for 4-bit addition, 5 gate delays after we are given a, b and Carry-In, we have calculated s and Carry-Out.

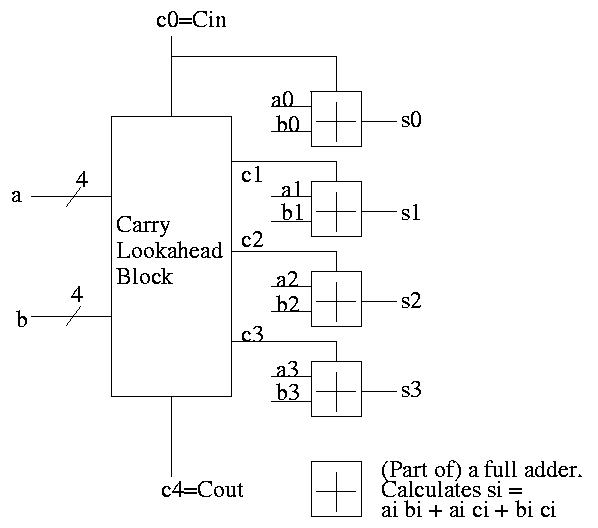
So, for 4-bit addition, the faster adder takes time 5 and the slower adder time 8.

Now we want to put four of these together to get a fast 16-bit adder.

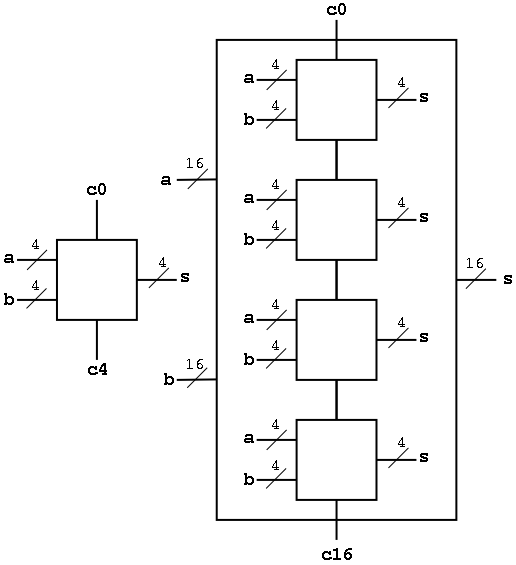
As black boxes, both ripple-carry adders and carry-lookahead adders (CLAs) look the same.

We could simply put four CLAs together and let the Carry-Out from one be the Carry-In of the next. That is, we could put these CLAs together in a ripple-carry manner to get a hybrid 16-bit adder.

• Since the Carry-Out is calculated in 3 gate delays, the Carry-In to the high order 4-bit adder is calculated in 3*3=9 delays.
• Hence the overall Carry-Out takes time 9+3=12 and the high order four bits of the sum take 9+5=14. The other bits take less time.
• So this mixed 16-bit adder takes 14 gate delays compared with 2*16=32 for a straight ripple-carry 16-bit adder.

We want to do better so we will put the 4-bit carry-lookahead adders together in a carry-lookahead manner. Thus the diagram above is not what we are going to do.

• We have 33 inputs a0,...,a15; b0,...b15; c0=Carry-In
• We want 17 outputs s0,...,s15; c16=c=Carry-Out
• Again we are assuming a gate can accept upto 5 inputs.
• It is important that the number of inputs per gate does not grow with the number of bits in each number.
• If the technology available supplies only 4-input gates (instead of the 5-input gates we are assuming), we would use groups of three bits rather than four

We start by determining ``super generate'' and ``super propagate'' bits.

• The super generate indicates whether the 4-bit adder constructed above generates a Carry-Out.
• The super propagate indicates whether the 4-bit adder constructed above propagates a Carry-In to a Carry-Out.

P0 = p3 p2 p1 p0          Does the low order 4-bit adder
                          propagate a carry?
P1 = p7 p6 p5 p4

P2 = p11 p10 p9 p8

P3 = p15 p14 p13 p12      Does the high order 4-bit adder
                          propagate a carry?


G0 = g3 + p3 g2 + p3 p2 g1 + p3 p2 p1 g0        Does low order 4-bit
                                                adder generate a carry
G1 = g7 + p7 g6 + p7 p6 g5 + p7 p6 p5 g4

G2 = g11 + p11 g10 + p11 p10 g9 + p11 p10 p9 g8

G3 = g15 + p15 g14 + p15 p14 g13 + p15 p14 p13 g12

From these super generates and super propagates, we can calculate the
super carries, i.e. the carries for the four 4-bit adders.

• The first super carry C0, the Carry-In to the low-order 4-bit adder, is just c0 the input Carry-In.
• The second super carry C1 is the Carry-Out of the low-order 4-bit adder (which is also the Carry-In to the 2nd 4-bit adder.
• The last super carry C4 is the Carry-out of the high-order 4-bit adder (which is also the overall Carry-out of the entire 16-bit adder).

C1 = G0 + P0 c0

C2 = G1 + P1 C1 = G1 + P1 G0 + P1 P0 c0

C3 = G2 + P2 C2 = G2 + P2 G1 + P2 P1 G0 + P2 P1 P0 c0

C4 = G3 + P3 C3 = G3 + P3 G2 + P3 P2 G1 + P3 P2 P1 G0 + P3 P2 P1 P0 c0

Now these C's (together with the original inputs a and b) are just what the 4-bit CLAs need.

How long does this take, again assuming 5 input gates?

1. We calculate the p's and g's (lower case) in 1 gate delay (as with the 4-bit CLA).
2. We calculate the P's one gate delay after we have the p's or 2 gate delays after we start.
3. The G's are determined 2 gate delays after we have the g's and p's. So the G's are done 3 gate delays after we start.
4. The C's are determined 2 gate delays after the P's and G's. So the C's are done 5 gate delays after we start.
5. Now the C's are sent back to the 4-bit CLAs, which have already calculated the p's and g's. The C's are calculated in 2 more gate delays (7 total) and the s's 2 more after that (9 total).

In summary, a 16-bit CLA takes 9 cycles instead of 32 for a ripple carry adder and 14 for the mixed adder.

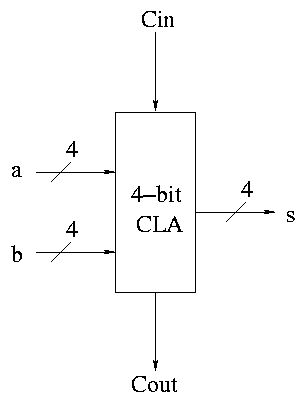
Some pictures follow.


Take our original picture of the 4-bit CLA and collapse the details so it looks like.

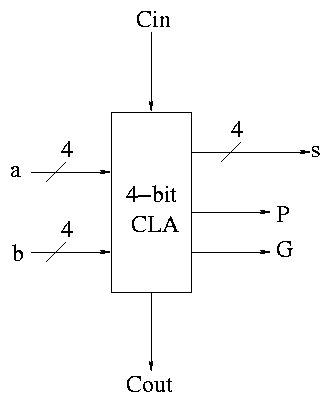
Next include the logic to calculate P and G.

Now put four of these with a CLA block (to calculate C's from P's, G's and C_in) and we get a 16-bit CLA. Note that we do not use the Cout from the 4-bit CLAs.

Note that the tall skinny box is general. It takes 4 Ps 4Gs and C_in and calculates 4Cs. The Ps can be propagates, superpropagates, superduperpropagates, etc. That is, you take 4 of these 16-bit CLAs and the same tall skinny box and you get a 64-bit CLA.

Homework: 44, 45