B.6: Finite State Machines (FSMs)

I do a different example from the book (counters instead of traffic lights). The ideas are the same and the two generic pictures (below) apply to both examples.

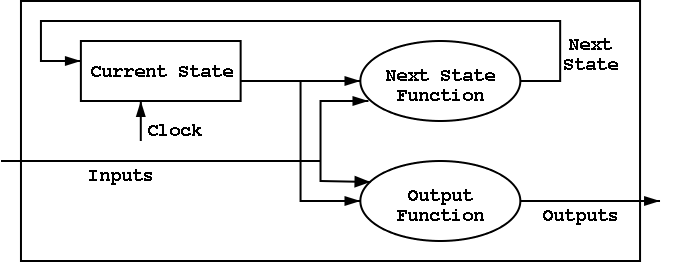
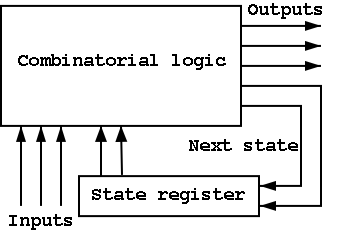
Counters

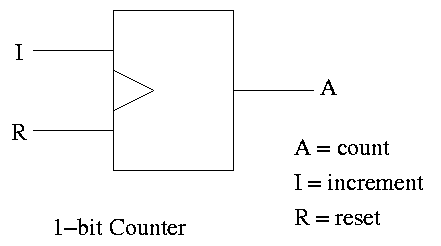
A counter counts (naturally).

• The counting is done in binary.
• Increments (i.e., counts) on clock ticks (active edge).
• Actually only on those clocks ticks when the ``increment'' line is asserted.
• If reset asserted at a clock tick, the counter is reset to zero.
• What if both reset and increment assert?
  Ans: Shouldn't do that. Will accept any answer (i.e., don't care).

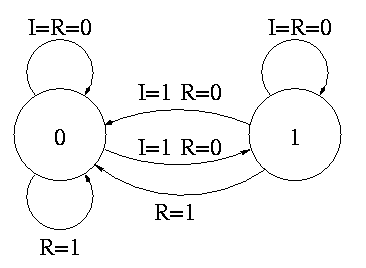
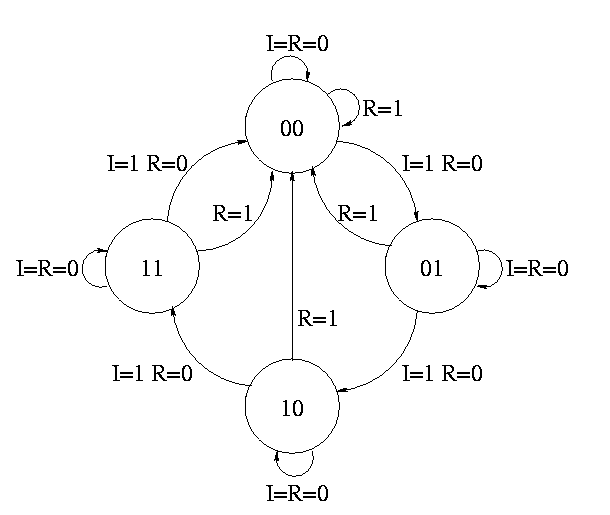
The state transition diagram

• The figure shows the state transition diagram for A, the output of a 1-bit counter.
• In this implementation, if R=I=1 we choose to set A to zero. That is, if Reset and Increment are both asserted, we do the Reset.

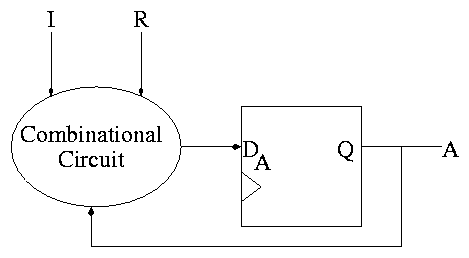
The circuit diagram.

• Uses one flop and a combinatorial circuit.
• The (combinatorial) circuit is determined by the transition diagram.
• The circuit must calculate the next value of A from the current value and I and R.
• The flop producing A is often itself called A and the D input to this flop is called D_A.
• To fit the diagram above for FSMs, we should not draw the overall output (A) coming from the flop (state register) but instead from the combinational circuit (which is easy since A is input to that circuit).

How do we determine the combinatorial circuit?

• This circuit has three inputs, I, R, and the current A.
• It has one output, D_A, which is the desired next A.
• So we draw a truth table, as before.
• For convenience I added the label Next A to the D_A column

Current      || Next A
   A    I R  || DA <-- i.e. to what must I set DA
-------------++--      in order to get the desired
   0    0 0  || 0      Next A for the next cycle.
   1    0 0  || 1      
   0    1 0  || 1
   1    1 0  || 0
   x    x 1  || 0

But this table is simply the truth table for the combinatorial circuit.

A I R  || DA
-------++--
0 0 0  || 0
1 0 0  || 1
0 1 0  || 1
1 1 0  || 0
x x 1  || 0

DA = R' (A XOR I)

How about a two bit counter.

• State diagram has 4 states 00, 01, 10, 11 and transitions from one to another.
• The circuit diagram has 2 D-flops.

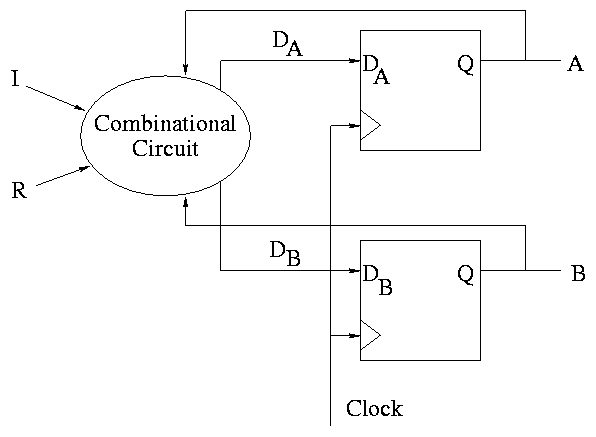
To determine the combinatorial circuit we could precede as before

Current      ||
  A B   I R  || DA DB
-------------++------

This would work but we can instead think about how a counter works and see that.

DA = R'(A XOR I)
DB = R'(B XOR AI)

Homework: B.23

B.7 Timing Methodologies

Skipped

Simulating Combinatorial Circuits at the Gate Level

The idea is, given a circuit diagram, write a program that behaves the way the circuit does. This means more than getting the same answer. The program is to work the way the circuit does.

For each logic box, you write a procedure with the following properties.

• A parameters is defined for each input and output wire.
• A (local) variable is defined for each internal wire.
  Really means a variable define for each signal. If a signal is sent from one gate to say 3 others, you might not call all those connections one wire, but it is one signal and is represented by one variable
• The only operations used are AND OR XOR NOT
  • In C or Java & | ^ !
  • Other languages similar.
  • Java is particularly well suited since it has variables and constants of type Boolean.
• An assignment statement (with an operator) corresponds to a gate.
  For example A = B & C; would mean that there is an AND gate with input wires B and C and output wire A.
• NO conditional assignment.
• NO if then else statements.
  We know how to implement a mux using ANDs, ORs, and NOTs.
• Single assignment to each variable.
  Multiple assignments would correspond to a cycle or to two outputs connected to the same wire.
• A bus (i.e., a set of signals) is represented by an array.
• Testing
  • Exhaustive possible for 1-bit cases.
  • Cleverness for n-bit cases (n=32, say).

Simulating a Full Adder

Remember that a full adder has three inputs and two outputs. Discuss FullAdder.c or perhaps FullAdder.java.

Simulating a 4-bit Adder

This implementation uses the full adder code above. Discuss FourBitAdder.c or perhaps FourBitAdder.java