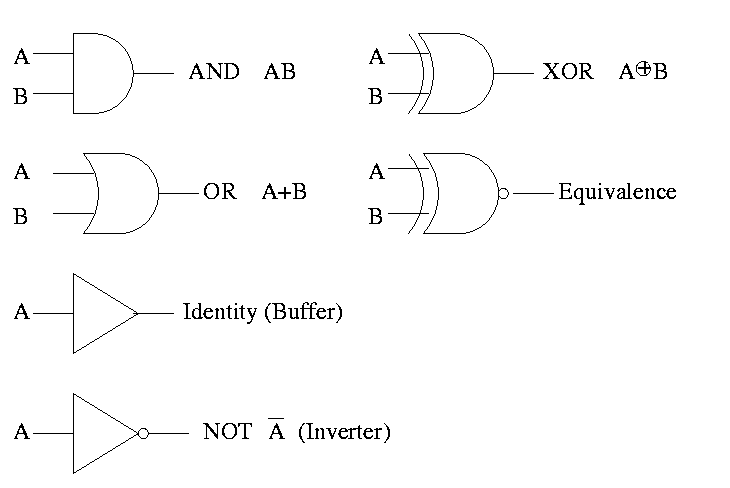
The first way we solved part E shows that any logic function can be written using just AND, OR, and NOT.

• Indeed, it is in a nice form, which is called two levels of logic.
• Each output is a sum of products of just inputs and their complements.
• That is it can be computed in just two time steps (assuming you already have the compliments).
• First compute all the needed products and then the single sums.

DeMorgan's laws:

• (A+B)' = A'B'
• (AB)' = A'+B'

You prove DM laws with TTs. Indeed that is ...

Homework: B.6 on page B-45.

Do beginning of HW on the board.

With DM (DeMorgan's Laws) we can do quite a bit without resorting to TTs. For example one can show that the two expressions for E in the example above (page B-6) are equal. Indeed that is

Homework: B.7 on page B-45

Do beginning of HW on board.

GATES

Gates implement the basic logic functions: AND OR NOT XOR Equivalence

We often omit the inverters and draw the little circles at the input or output of the other gates (AND OR). These little circles are sometimes called bubbles.

This explains why the inverter is drawn as a buffer with a bubble.

Show why the picture for equivalence is the negation of XOR, i.e (A XOR B)' is AB + A'B'

(A XOR B)' =
(A'B+AB')' = 
(A'B)' (AB')' = 
(A''+B') (A'+B'') = 
(A + B') (A' + B) = 
AA' + AB + B'A' + B'B = 
0   + AB + B'A' + 0 = 
AB + A'B'

Homework: B.2 on page B-45 (I previously did the first part of this homework).

Homework: Consider the Boolean function of 3 boolean vars (i.e. a three input function) that is true if and only if exactly 1 of the three variables is true. Draw the TT. Draw the logic diagram with AND OR NOT. Draw the logic diagram with AND OR and bubbles.

A set of gates is called universal if these gates are sufficient to generate all logic functions.

• We have seen that any logic function can be constructed from AND OR NOT. So this triple is universal.
• Are there any pairs that are universal?
  Ans: Sure, A+B = (A'B')' so can get OR from AND and NOT. Hence the pair AND NOT is universal
  Similarly, can get AND from OR and NOT and hence the pair OR NOT is universal
• Could there possibly be a single function that is universal all by itself?
  AND won't work as you can't get NOT from just AND
  OR won't work as you can't get NOT from just OR
  NOT won't work as you can't get AND from just NOT.
• But there indeed is a universal function! In fact there are two.

NOR (NOT OR) is true when OR is false. Do TT.

NAND (NOT AND) is true when AND is false. Do TT.

Draw two logic diagrams for each, one from the definition and an equivalent one with bubbles.

Theorem A 2-input NOR is universal and a 2-input NAND is universal.

Proof

We must show that you can get A', A+B, and AB using just a two input NOR.

• A' = A NOR A
• A+B = (A NOR B)' (we can use ' by above)
• AB = (A' OR B')'

Homework: Show that a 2-input NAND is universal.

Can draw NAND and NOR each two ways (because (AB)' = A' + B')

We have seen how to get a logic function from a TT. Indeed we can get one that is just two levels of logic. But it might not be the simplest possible. That is, we may have more gates than are necessary.

Trying to minimize the number of gates is NOT trivial. Mano covers the topic of gate minimization in detail. We will not cover it in this course. It is not in H&P. I actually like it but must admit that it takes a few lectures to cover well and it not used much in practice since it is algorithmic and is done automatically by CAD tools.

Minimization is not unique, i.e. there can be two or more minimal forms.

Given A'BC + ABC + ABC'
Combine first two to get BC + ABC'
Combine last two to get A'BC + AB

Sometimes when building a circuit, you don't care what the output is for certain input values. For example, that input combination might be known not to occur. Another example occurs when, for some combination of input values, a later part of the circuit will ignore the output of this part. These are called don't care outputs. Making use of don't cares can reduce the number of gates needed.

Can also have don't care inputs when, for certain values of a subset of the inputs, the output is already determined and you don't have to look at the remaining inputs. We will see a case of this in the very next topic, multiplexors.

An aside on theory

Putting a circuit in disjunctive normal form (i.e. two levels of logic) means that every path from the input to the output goes through very few gates. In fact only two, an OR and an AND. Maybe we should say three since the AND can have a NOT (bubble). Theorticians call this number (2 or 3 in our case) the depth of the circuit. Se we see that every logic function can be implemented with small depth. But what about the width, i.e., the number of gates.

The news is bad. The parity function takes n inputs and gives TRUE if and only if the number of TRUE inputs is odd. If the depth is fixed (say limited to 3), the number of gates needed for parity is exponential in n.

B.3 COMBINATIONAL LOGIC

Homework: Read B.3.

Generic Homework: Read sections in book corresponding to the lectures.

Multiplexor

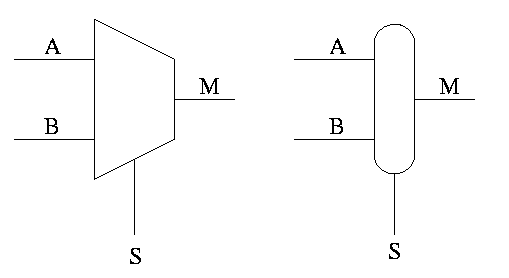
Often called a mux or a selector

Show equivalent circuit with AND OR

Hardware if-then-else

    if S=0
        M=A
    else
        M=B
    endif

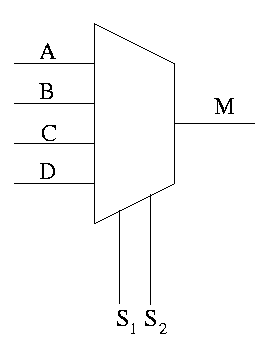
This is an if-then-elif-elif-else

   if S1=0 and S2=0
        M=A
    elif S1=0 and S2=1
        M=B
    elif S1=1 and S2=0
        M=C
    else -- S1=1 and S2=1
        M=D
    endif

Do a TT for 2 way mux. Redo it with don't care values.
Do a TT for 4 way mux with don't care values.

Homework: B.12.
B.5 (Assume you have constant signals 1 and 0 as well.)

Decoder

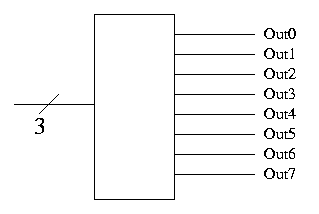
Basically, the opposite of a mux.

• Note the ``3'' with a slash, which signifies a three bit input. This notation represents three (1-bit) wires.
• A decoder with n input bits, produces 2^n output bits.
• View the input as ``k written an n-bit binary number'' and view the output as 2^n bits with the k-th bit set and all the other bits clear.
• Implement on board with AND/OR.
• Why do we use decoders and encoders?
  • The encoded form takes (MANY) fewer bits so is better for communication.
  • The decoded form is easier to work with in hardware since there is no direct way to test if 8 wires represent a 5 (101). You would have to test each wire. But it easy to see if the encoded form is a five (00100000)