2.4: Process Scheduling

Scheduling the processor is often called ``process scheduling'' or simply ``scheduling''.

The objectives of a good scheduling policy include

• Fairness.
• Efficiency.
• Low response time (important for interactive jobs).
• Low turnaround time (important for batch jobs).
• High throughput [the above are from Tanenbaum].
• Repeatability. Dartmouth (DTSS) ``wasted cycles'' and limited logins for repeatability.
• Fair across projects.
  • ``Cheating'' in unix by using multiple processes.
  • TOPS-10.
  • Fair share research project.
• Degrade gracefully under load.

Recall the basic diagram describing process states

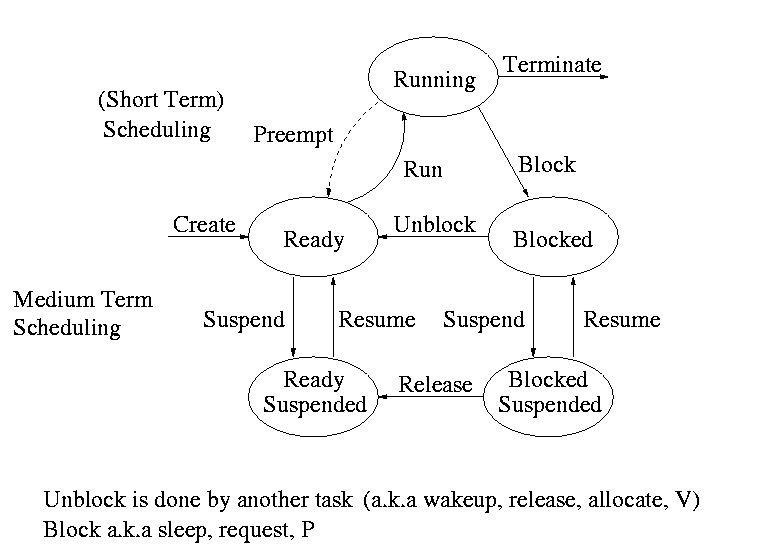
For now we are discussing short-term scheduling, i.e., the arcs connecting running <--> ready.

Medium term scheduling is discussed later.

Preemption

It is important to distinguish preemptive from non-preemptive scheduling algorithms.

• Preemption means the operating system moves a process from running to ready without the process requesting it.
• Without preemption, the system implements ``run to completion (or yield or block)''.
• The ``preempt'' arc in the diagram.
• We do not consider yield (a solid arrow from running to ready).
• Preemption needs a clock interrupt (or equivalent).
• Preemption is needed to guarantee fairness.
• Found in all modern general purpose operating systems.
• Even non preemptive systems can be multiprogrammed (e.g., when processes block for I/O).

Deadline scheduling

This is used for real time systems. The objective of the scheduler is to find a schedule for all the tasks (there are a fixed set of tasks) so that each meets its deadline. The run time of each task is known in advance.

Actually it is more complicated.

• Periodic tasks
• What if we can't schedule all task so that each meets its deadline (i.e., what should be the penalty function)?
• What if the run-time is not constant but has a known probability distribution?

We do not cover deadline scheduling in this course.

The name game

There is an amazing inconsistency in naming the different (short-term) scheduling algorithms. Over the years I have used primarily 4 books: In chronological order they are Finkel, Deitel, Silberschatz, and Tanenbaum. The table just below illustrates the name game for these four books. After the table we discuss each scheduling policy in turn.

Finkel  Deitel  Silbershatz Tanenbaum
-------------------------------------
FCFS    FIFO    FCFS        --    unnamed in tanenbaum
RR      RR      RR          RR
PS      **      PS          PS
SRR     **      SRR         **    not in tanenbaum
SPN     SJF     SJF         SJF
PSPN    SRT     PSJF/SRTF   --    unnamed in tanenbaum
HPRN    HRN     **          **    not in tanenbaum
**      **      MLQ         **    only in silbershatz
FB      MLFQ    MLFQ        MQ

First Come First Served (FCFS, FIFO, FCFS, --)

If the OS ``doesn't'' schedule, it still needs to store the PTEs somewhere. If it is a queue you get FCFS. If it is a stack (strange), you get LCFS. Perhaps you could get some sort of random policy as well.

• Only FCFS is considered.
• The simplist scheduling policy.
• Non-preemptive.

Round Robbin (RR, RR, RR, RR)

• An important preemptive policy.
• Essentially the preemptive version of FCFS.
• The key parameter is the quantum size q.
• When a process is put into the running state a timer is set to q.
• If the timer goes off and the process is still running, the OS preempts the process.
  • This process is moved to the ready state (the preempt arc in the diagram), where it is placed at the rear of the ready list (a queue).
  • The process at the front of the ready list is removed from the ready list and run (i.e., moves to state running).
• When a process is created, it is placed at the rear of the ready list.
• As q gets large, RR approaches FCFS
• As q gets small, RR approaches PS (Processor Sharing, described next)
• What value of q should we choose?
  • Tradeoff
  • Small q makes system more responsive.
  • Large q makes system more efficient since less process switching.

Homework: 9, 19, 20, 21, and the following (remind me to discuss this last one in class next time):

Consider the set of processes in the table below. When does each process finish if RR scheduling is used with q=1, if q=2, if q=3, if q=100. First assume (unrealistically) that context switch time is zero. Then assume it is .1. Each process performs no I/O (i.e., no process ever blocks). All times are in milliseconds. The CPU time is the total time required for the process (excluding context switch time). The creation time is the time when the process is created. So P1 is created when the problem begins and P2 is created 5 miliseconds later.

Process	CPU Time	Creation Time
P1	20	0
P2	3	3
P3	2	5

Processor Sharing (PS, **, PS, PS)

Merge the ready and running states and permit all ready jobs to be run at once. However, the processor slows down so that when n jobs are running at once each progresses at a speed 1/n as fast as it would if it were running alone.

• Clearly impossible as stated due to the overhead of process switching.
• Of theoretical interest (easy to analyze).
• Approximated by RR when the quantum is small. Make sure you understand this last point. For example, consider the last homework assignment (with zero context switch time) and consider q=1, q=.1, q=.01, etc.

Homework: 18. (part of homework #8 as #7 has enough)

Variants of Round Robbin

• State dependent RR
  • Same as RR but q is varied dynamically depending on the state of the system.
  • Favor processes holding important resources.
    • For example, non-swappable memory.
    • Perhaps this should be considered medium term scheduling since you probably do not recalculate q each time.
• External priorities: RR but a user can pay more and get bigger q. That is one process can be given a higher priority than another. But this is not an absolute priority, i.e., the lower priority (i.e., less important) process does get to run, but not as much as the high priority process.

Priority Scheduling

Each job is assigned a priority (externally, perhaps by charging more for higher priority) and the highest priority ready job is run.

• Similar to ``External priorities'' above
• If many processes have the highest priority, use RR among them.
• Can easily starve processes (see aging below for fix).
• Can have the priorities changed dynamically to favor processes holding important resources (similar to state dependent RR).
• Many policies can be thought of as priority scheduling in which we run the job with the highest priority (with different notions of priority for different policies).

Priority aging

As a job is waiting, raise its priority so eventually it will have the maximum priority.

• This prevents starvation (assuming all jobs terminate). policy is preemptive).
• There may be many processes with the maximum priority.
• If so, can use fifo among those with max priority (risks starvation if a job doesn't terminate) or can use RR.
• Can apply priority aging to many policies, in particular to priority scheduling described above.