Now we augment the ALU so that we can perform subtraction (as well as addition, AND, and OR).

• Big deal about 2's compliment is that
  A - B = A + (2's comp B) = A + (B' + 1).
• Get B' from an inverter (naturally).
• Get +1 from the CarryIn.

1-bit ALU with ADD, SUB, AND, OR is

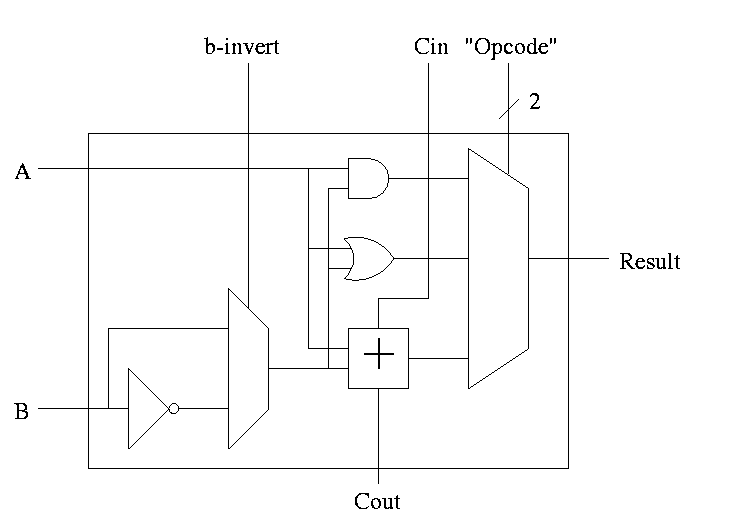
Implementing addition and subtraction

1. To implement addition we use opcode 10 as before and de-assert both b-invert and Cin.
2. To implement subtraction we still use opcode 10 but we assert both b-invert and Cin.

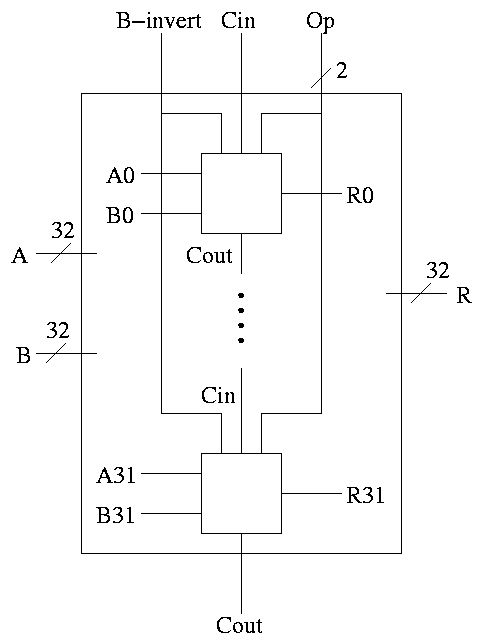
32-bit version is simply a bunch of these.

• For subtraction assert both B-invert and Cin.
• For addition de-assert both B-invert and Cin.
• For AND and OR de-assert B-invert. Cin is a don't care.
• We get for free A+B'
  If we let A=0, this gives B', i.e. the NOT operation
  However, we will not use it. Indeed we will soon give it away.

(More or less) all ALUs do AND, OR, ADD, SUB. Now we want to customize our ALU for the MIPS architecture. Extra requirements for MIPS ALU:

1. slt set-less-than
   
   
   • Result reg is 1 if a < b
     Result reg is 0 if a >= b
     
     
   • So need to set the LOB (low order bit, aka least significant bit) of the result equal to the sign bit of a subtraction, and set the rest of the result bits to zero.
     
     
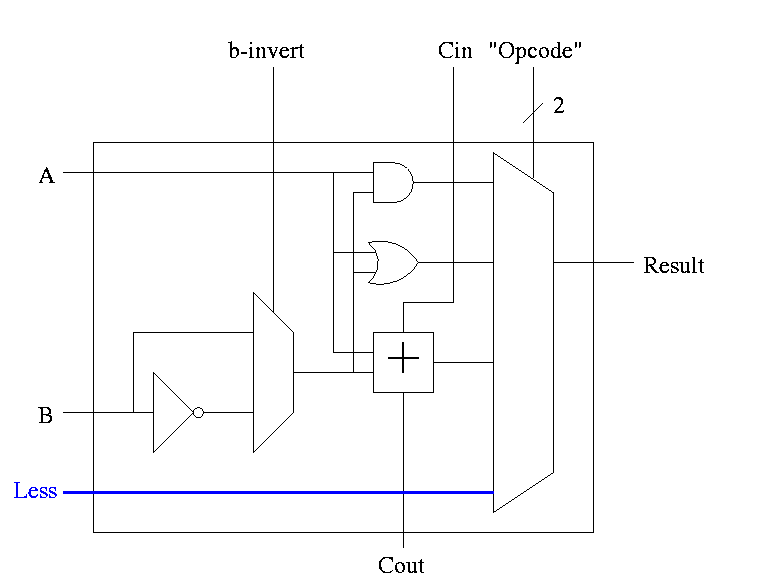
   • Idea #1. Give the mux another input, called LESS. This input is brought in from outside the bit cell. That is, if the opcode is slt we make the select line to the mux equal to 11 (three) so that the the output is the this new input. For all the bits except the LOB, the LESS input is zero. For the LOB we must figure out how to set LESS.
   
   

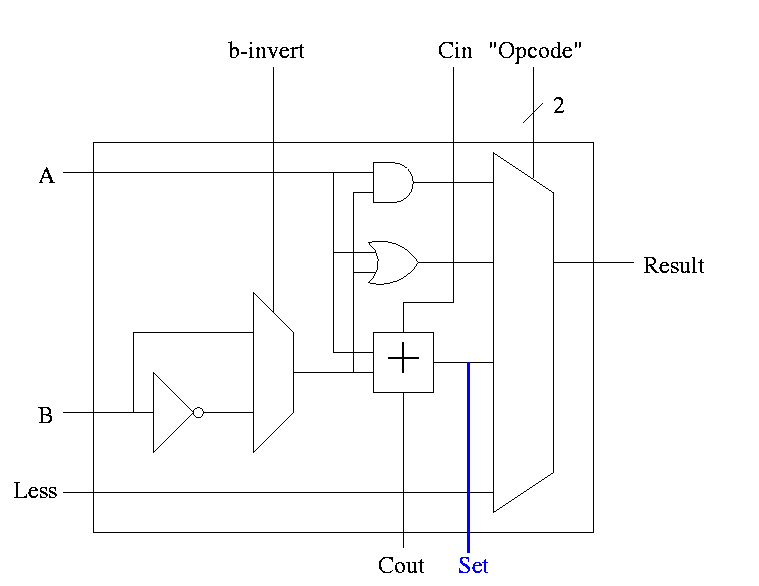
• Idea #2. Bring out the result of the adder (BEFORE the mux)
  
  Only needed for the HOB (high order bit, i.e. sign) Take this new output from the HOB, call it SET and connect it to the LESS input in idea #1 for the LOB. The LESS input for other bits are set to zero.
  
  

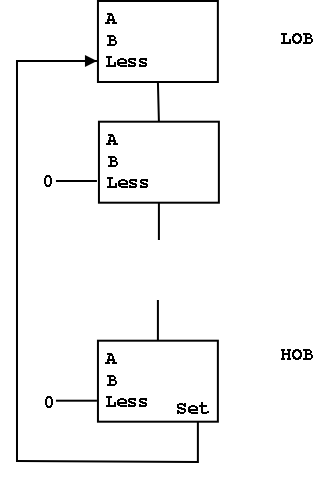
• Why isn't this method used?
  
  
• Ans: It is wrong!
  
  
• Example using 3 bit numbers (i.e. -4 .. 3).
  • Try slt on -3 and +2.
  • True subtraction (-3 - +2) gives -5.
  • The negative sign in -5 indicates (correctly) that -3 < +2.
  • But three bit subtraction -3 - +2 gives +3 !
  • Hence we will incorrectly conclude that -3 is NOT less than +2.
  • (Really, the subtraction signals an overflow. unless doing unsigned)
  
  
• Solution: Need the correct rule for less than (not just sign of subtraction).
  
  
Homework: figure out correct rule, i.e. prob 4.23. Hint: when an overflow occurs the sign bit is definitely wrong (so the complement of the sign bit is right).
2. Overflows
   • The HOB ALU is already unique (outputs SET).
   • Need to enhance it some more to produce the overflow output.
   • Recall that we gave the rule for overflow. You need to examine:
     • Whether the operation is add or sub (binvert).
     • The sign of A.
     • The sign of B.
     • The sign of the result.
     • Since this is the HOB we have all the sign bits.
     • The book also uses Cout, but this appears to be an error.
   
   





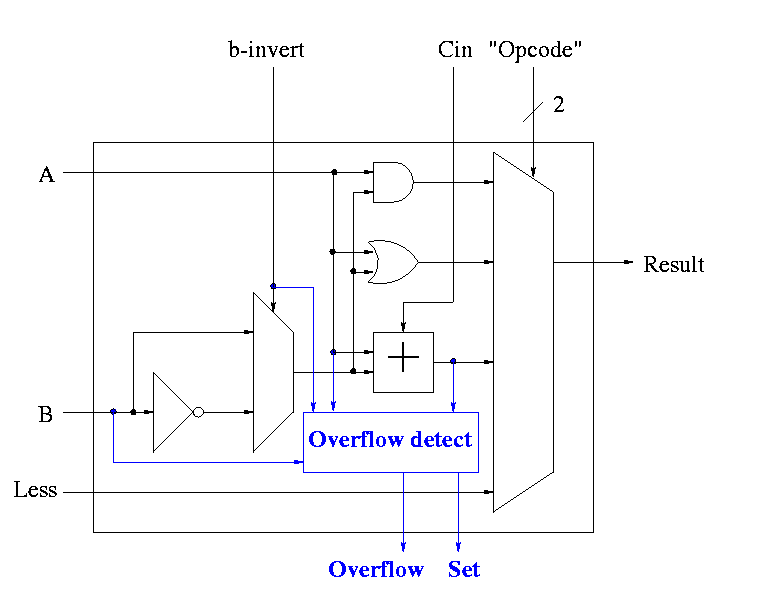
• Simpler overflow detection.
  • An overflow occurs if and only if the carry in to the HOB differs from the carry out of the HOB.
  
  





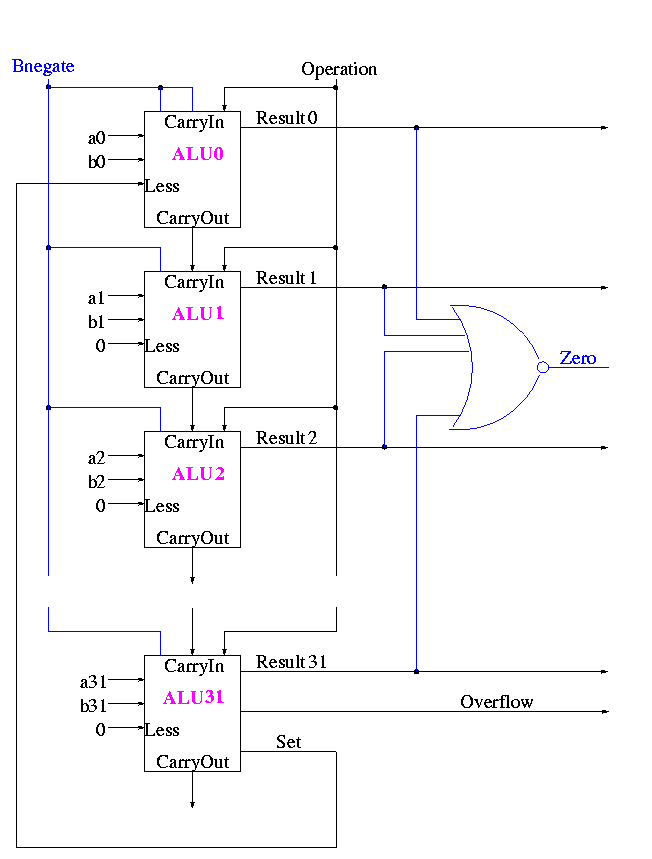
3. Zero Detect
   • To see if all bits are zero just need NOR of all the bits
   • Conceptually trivially but does require some wiring
   
   
4. Observation: The initial Cin and Binvert are always the same. So just use one input called Bnegate.

The Final Result is





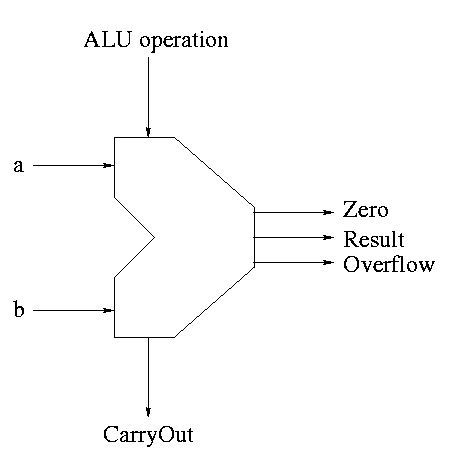
The symbol used for an ALU is on the right

What are the control lines?

• Bnegate (1 bit)
• OP (2 bits)

What functions can we perform?

• and
• or
• add
• sub
• set on less than

What (3-bit) values for the control lines do we need for each function? The control lines are Bnegate (1-bit) and Operation (2-bits)

and	0	00
or	0	01
add	0	10
sub	1	10
slt	1	11