blt (branch if less than)

• I-type
• if reg5 < reg8 then go to the 124rd instruction after this one.
• *** WRONG ***
• There is no blt instruction.
• Instead use

      stl $1,$5,$8
      bne $1,$0,123
  

ble (branch if less than or equal)

• There is no ``ble $5,$8,L'' instruction.
• There is also no ``sle $1,$5,$8'' set $1 if $5 less or equal $8.
• Note that $5<=$8 <==> NOT ($8<$5).
• Hence we test for $8<$5 and branch if false.

      stl $1,$8,$5
      beq $1,$0,L
  

bgt (branch if greater than>

• There is no ``bgt $5,$8,L'' instruction.
• There is also no ``sgt $1,$5,$8'' set $1 if $5 greater than $8.
• Note that $5>$8 <==> $8<$5.
• Hence we test for $8<$5 and branch if true.

      stl $1,$8,$5
      bne $1,$0,L
  

bge (branch if greater than or equal>

• There is no ``bge $5,$8,L'' instruction.
• There is also no ``sge $1,$5,$8'' set $1 if $5 greater or equal $8l
• Note that $5>=$8 <==> NOT ($5<$8)l
• Hence we test for $5<$8 and branch if false.

      stl $1,$5,$8
      beq $1,$0,L
  

Note: Please do not make the mistake of thinking that

    stl $1,$5,$8
    beq $1,$0,L

    stl $1,$8,$5
    bne $1,$0,L

The negation of X < Y is not Y < X

End of Note

Homework: 3.12-3.17

J-type instructions (J for jump)

        op   address
        6     26

j (jump)

Example: j 10000

• Jump to instruction (not byte) 10000.
• Branches are PC relative, jumps are absolute.
• J type
• Range is 2^26 words = 2^28 bytes = 1/4 GB

jr (jump register)

Example: jr $10

• Jump to the location in register 10.
• R type, but uses only one register.
• Will it use one of the source registers or the destination register?
  Ans: This will be obvious when we construct the processor.

jal (jump and link)

Example: jal 10000

• Jump to instruction 10000 and store the return address (the address of the instruction after the jal).
• Used for subroutine calls.
• J type.
• Return address is stored in register 31. By using a fixed register, jal avoids the need for a second register field and hence can have 26 bits for the instruction address (i.e., can be a J type).

I type instructions (revisited)

• The I is for immediate.
• These instructions have an immediate third operand, i.e., the third operand is contained in the instruction itself.
• This means the operand itself, and not just its address or register number, is contained in the instruction.
• Two registers and one immediate operand.
• Compare I and R types: Since there is no shamt and no funct, the immediate field can be larger than the field for a register.
• Recall that lw and sw were I type. They had an immediate operand, the offset added to the register to specify the memory address.

addi (add immediate)

Example: addi $1,$2,100

• $1 = $2 + 100
• Why is there no subi?
  Ans: Make the immediate operand negative.

slti (set less-than immediate)

Example slti $1,$2,50

• Set $1 to 1 if $2 less than 50; set $1 to 0 otherwise.

lui (load upper immediate)

Example: lui $4,123

• Loads 123 into the upper 16 bits of register 4 and clears the lower 16 bits of the register.
• What is the use of this instruction?
• How can we get a 32-bit constant into a register since we can't have a 32 bit immediate?
  1. Load the word
     • Have the constant placed in the program text (via some assembler directive).
     • Issue lw to load the register.
     • But memory accesses are slow and this uses a cache entry.
  2. Load shift add
     1. Load immediate the high order 16 bits (into the low order of the register).
     2. Shift the register left 16 bits (filling low order with zero)
     3. Add immediate the low order 16 bits
     4. Three instructions, three words of memory
  3. load-upper add
     • Use lui to load immediate the desired 16-bit value into the high order 16 bits of the register and clear the low order bits.
     • Add immediate the desired low order 16 bits.
     • lui $4,123 -- puts 123 into top half of register 4.
       addi $4,$4,456 -- puts 456 into bottom half of register 4.
       

Homework: 3.1, 3.3-3.7, 3.9, 3.18, 3.37 (for fun)

Chapter 4

Homework: Read 4.1-4.4

Homework: 4.1-4.9

4.2: Signed and Unsigned Numbers

MIPS uses 2s complement (just like 8086)

To form the 2s complement (of 0000 1111 0000 1010 0000 0000 1111 1100)

• Take the 1s complement.
• That is, complement each bit (1111 0000 1111 0101 1111 1111 0000 0011)
• Then add 1 (1111 0000 1111 0101 1111 1111 0000 0100)

Need comparisons for signed and unsigned.

• For signed a leading 1 is smaller (negative) than a leading 0
• For unsigned a leading 1 is larger than a leading 0

sltu and sltiu

Just like slt and slti but the comparison is unsigned.

4.3: Addition and subtraction

To add two (signed) numbers just add them. That is don't treat the sign bit special.

To subtract A-B, just take the 2s complement of B and add.

Overflows

An overflow occurs when the result of an operatoin cannot be represented with the available hardware. For MIPS this means when the result does not fit in a 32-bit word.

• We have 31 bits plus a sign bit.
• The result would definitely fit in 33 bits (32 plus sign)
• The hardware simply discards the carry out of the top (sign) bit
• This is not wrong--consider -1 + -1

    11111111111111111111111111111111   (32 ones is -1)
  + 11111111111111111111111111111111
  ----------------------------------
   111111111111111111111111111111110   Now discard the carry out
  
    11111111111111111111111111111110   this is -2
  

• The bottom 31 bits are always correct.
  Overflow occurs when the 32 (sign) bit is set to a value and not the sign.
• Here are the conditions for overflow

  Operation  Operand A  Operand B  Result
     A+B       >= 0        >= 0      < 0
     A+B        < 0         < 0     >= 0
     A-B       >= 0         < 0      < 0
     A-B        < 0        >= 0     >= 0
  

• These conditions are the same as
  CarryIn to sign position != CarryOut

Homework: Prove this last statement (4.29) (for fun only, do not hand in).

addu, subu, addiu

These add and subtract the same as add and sub, but do not signal overflow

4.4: Logical Operations

Shifts: sll, srl

• R type, with shamt used and rs not used.
• sll $1,$2,5
  reg2 gets reg1 shifted left 5 bits.
• Why do we need both sll and srl, i.e, why not just have one of them and use a negative shift amt for the other?
  Ans: The shift amt is only 5 bits and need shifts from 0 to 31 bits. Hence not enough bits for negative shifts.
• These are shifts not rotates.
• Op is 0 (these are ALU ops, will understand why in a few weeks).

Bitwise AND and OR: and, or, andi, ori

No surprises.

• and $r1,$r2,$r3
  or $r1,$r2,$r3
• standard R-type instruction
• andi $r1,$r2,100
  ori $r1,$r2,100
  
• standard I-type

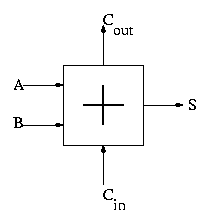
4.5: Constructing an ALU--the fun begins

Recall we know how to build a full adder. We will draw it as shown on the right.

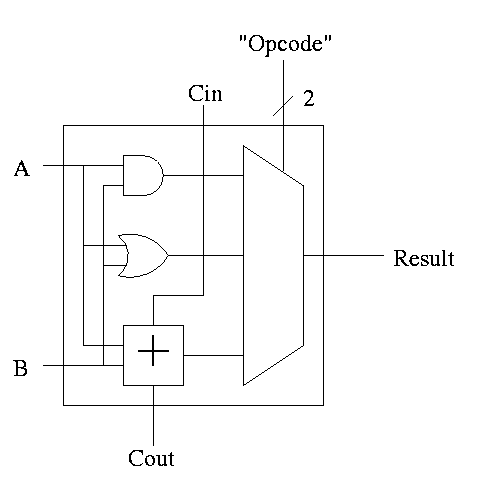
With this adder, the ALU is easy.

• Just choose the correct operation (ADD, AND, OR)
• Note the principle that if you want a logic box that sometimes computes X and sometimes computes Y, what you do is
  1. Always compute X.
  2. Always compute Y.
  3. Put both X and Y into a mux.
  4. Use the ``sometimes'' condition as the select line to the mux.

1. Use an array of logic elements for the logic. The logic element is the 1-bit ALU
2. Use buses for A, B, and Result.
3. ``Broadcast'' Opcode to all of the internal 1-bit ALUs. This means wire the external Opcode to the Opcode input of each of the internal 1-bit ALUs

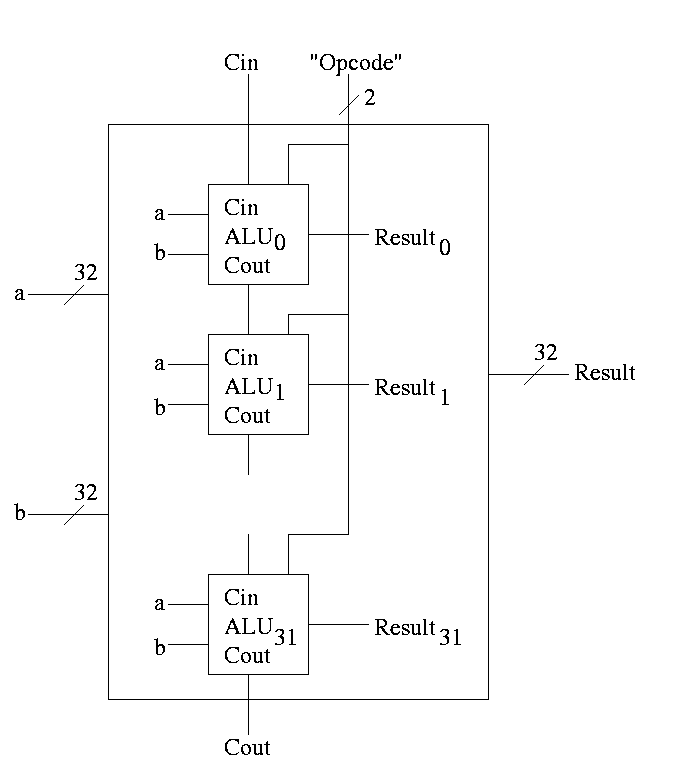
First goal accomplished.