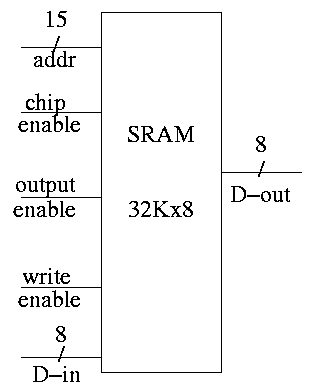
SRAMS and DRAMS

• External interface is on right
  • 32Kx8 means it hold 32K words each 8 bits.
  • Addr, D-in, and D-out are same as registers. Addr is 15 bits since 2 ^ 15 = 32K. D-out is 8 bits since we have a by 8 SRAM.
  • Write enable is similar to the write line (unofficial: it is a pulse; there is no clock),
  • Output enable is for the three state (tri-state) drivers discussed just below (unofficial).
  • Ignore chip enable (perfer not to have all chips enabled for electrical reasons).
• (Sadly) we will not look inside officially. Following is unofficial
  • Conceptually, an SRAM is like a register file but we can't use the register file implementation for a large SRAM because there would be too many wires and the muxes would be too big.
  • Two stage decode.
    • For a 32Kx8 SRAM would need a 15-32K decoder.
    • Instead package the SRAM as eight 512x64 SRAMS.
    • Pass 9 bits of the address through a 9-512 decoder and use these 512 wires to select the appropriate 64-bit word from each of the sub SRAMS. Use the remaining 6 bits to select the appropriate bit from each 64-bit word.
  • Tri-state buffers (drivers) used instead of a mux.
    • I was fibbing when I said that signals always have a 1 or 0.
    • However, we will not use tristate logic; we will use muxes.
  • DRAM uses a version of the above two stage decode.
    • View the memory as an array.
    • First select (and save in a ``faster'' memory) an entire row.
    • Then select and output only one (or a few) column(s).
    • So can speed up access to elts in same row.
  • SRAM and ``logic'' are made from similar technologies but DRAM technology is quite different.
    • So easy to merge SRAM and CPU on one chip (SRAM cache).
    • Merging DRAM and CPU is more difficult but is now being done.
• Error Correction (Omitted)

Note: There are other kinds of flip-flops T, J-K. Also one could learn about excitation tables for each. We will not cover this material (H&P doesn't either). If interested, see Mano

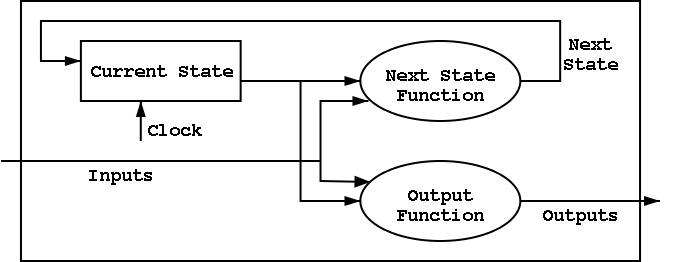
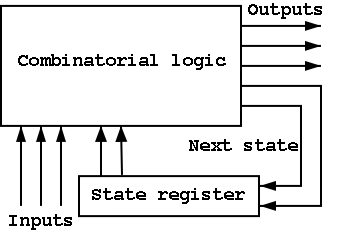
B.6: Finite State Machines

I do a different example from the book (counters instead of traffic lights). The ideas are the same and the two generic pictures (below) apply to both examples.

Counters

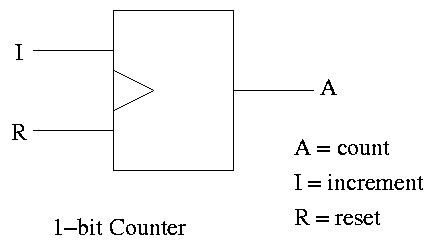
A counter counts (naturally).

• The counting is done in binary.
• Increments (i.e., counts) on clock ticks (active edge).
• Actually only on those clocks ticks when the ``increment'' line is asserted.
• If reset asserted at a clock tick, the counter is reset to zero.
• What if both reset and increment assert?
  Ans: Shouldn't do that. Will accept any answer (i.e., don't care).

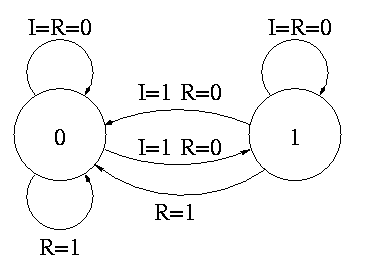
The state transition diagram

• The figure shows the state transition diagram for A, the output of a 1-bit counter.
• In this implementation, if R=I=1 we choose to set A to zero. That is, if Reset and Increment are both asserted, we do the Reset.

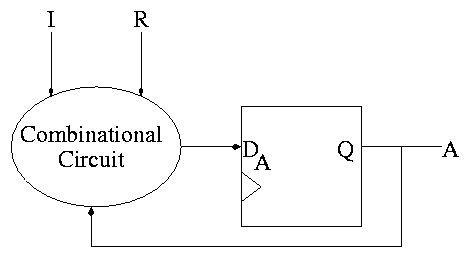
The circuit diagram.

• Uses one flop and a combinatorial circuit.
• The (combinatorial) circuit is determined by the transition diagram.
• The circuit must calculate the next value of A from the current value and I and R.
• The flop producing A is often itself called A and the D input to this flop is called DA (really D sub A).

How do we determine the combinatorial ciccuit?

• This circuit has three inputs, I, R, and the current A.
• It has one output, DA, which is the desired next A.
• So we draw a truth table, as before.
• For convenience I added the label Next A to the DA column

Current      || Next A
   A    I R  || DA <-- i.e. to what must I set DA
-------------++--      in order to get the desired
   0    0 0  || 0      Next A for the next cycle.
   1    0 0  || 1      
   0    1 0  || 1
   1    1 0  || 0
   x    x 1  || 0

But this table is simply the truth table for the combinatorial circuit.

A I R  || DA
-------++--
0 0 0  || 0
1 0 0  || 1
0 1 0  || 1
1 1 0  || 0
x x 1  || 0

DA = R' (A XOR I)

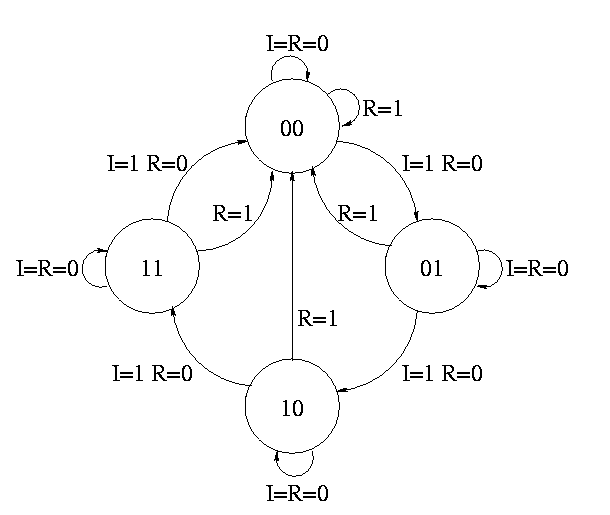
How about a two bit counter.

• State diagram has 4 states 00, 01, 10, 11 and transitions from one to another
• The circuit diagram has 2 D flops

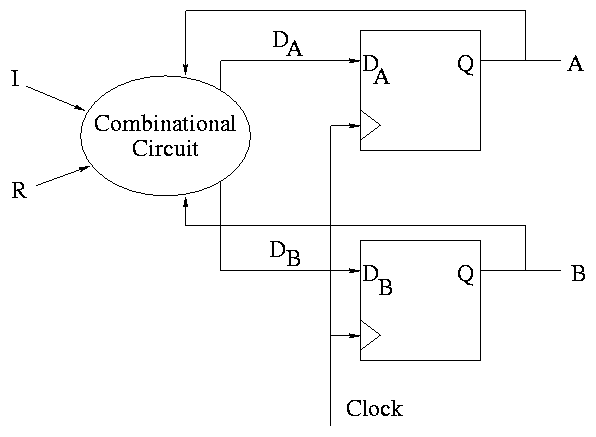
To determine the combinationatorial circuit we could preceed as before

Current      ||
  A B   I R  || DA DB
-------------++------

This would work but we can instead think about how a counter works and see that.

DA = R'(A XOR I)
DB = R'(B XOR AI)

Homework: 23

B.7 Timing Methodologies

Skipped

Chapter 1

Homework: READ chapter 1. Do 1.1 -- 1.26 (really one matching question)
Do 1.27 to 1.44 (another matching question),
1.45 (and do 7200 RPM and 10,000 RPM), 1.46, 1.50

Chapter 3

Homework: Read sections 3.1 3.2 3.3