ROMs

One way to implement a mathematical (or C) function (without side effects) is to perform a table lookup.

A ROM (Read Only Memory) is the analogous way to implement a logic function.

• For a math function f we start with x and get f(x).
• For a ROM with start with the address and get the value stored at that address.
• Normally math functions are defined for an infinite number of values, for example f(x) = 3x for all real numbers x
• We can't build an infinite ROM (sorry), so we are only interested in functions defined for a finite number of values. Today a million is OK a billion is too big.
• How do we create a ROM for the function f(3)=4, f(6)=20 all other values don't care?
  Simply have the ROM store 4 in address 3 and 20 in address 6.
• Consider a function defined for all n-bit numbers (say n=20) and having a k-bit output for each input.
  • View an n-bit input as n 1-bit inputs.
  • View a k-bit output as k 1-bit outputs.
  • Since there are 2^n possible inputs and each requires a k 1-bit output, there are a total of (2^n)k bits of output, i.e. the ROM must hold (2^n)k bits.
  • Now consider a truth table with n inputs and k outputs. The total number of output bits is again (2^n)k (2^n rows and k output columns).
• Thus the ROM implements a truth table, i.e. is a logic function.

Important: A ROM does not have state. It is another combinational circuit. That is, it does not represent ``memory''. The reason is that once a ROM is manufactured, the output depends only on the input.

A PROM is a programmable ROM. That is you buy the ROM with ``nothing'' in its memory and then before it is placed in the circuit you load the memory, and never change it. This is like a CD-R.

An EPROM is an erasable PROM. It costs more but if you decide to change its memory this is possible (but is slow). This is like a CD-RW.

``Normal'' EPROMs are erased by some ultraviolet light process. But EEPROMs (electrically erasable PROMS) are faster and are done electronically.

All these EPROMS are erasable not writable, i.e. you can't just change one bit.

A ROM is similar to PLA

• Both can implement any truth table, in principle.
• A 2Mx8 ROM can really implment any truth table with 21 inputs (2^21=2M) and 8 outputs.
  • It stores 2M bytes
  • In ROM-speak, it has 21 address pins and 8 data pins
• A PLA with 21 inputs and 8 outputs might need to have 2M minterms (AND gates).
  • The number of minterms depends on the truth table itself.
  • For normal TTs with 21 inputs the number of minterms is MUCH less than 2^21.
  • The PLA is manufactured with the number of minterms needed
• Compare a PAL with a PROM
  • Both can in principle implement any TT
  • Both are user programmable
  • A PROM with n inputs and k outputs can implement any TT with n inputs and k outputs.
  • A PAL that you buy does not have enough gates for all possibilities since most TTs with n inputs and k outputs don't require nearly (2^n)k gates.

Don't Cares

• Sometimes not all the input and output entries in a TT are needed. We indicate this with an X and it can result in a smaller truth table.
• Input don't cares.
  • The output doesn't depend on all inputs, i.e. the output has the same value no matter what value this input has.
  • We saw this when we did muxes
• Output don't cares
  • For some input values, either output is OK.
    • This input combination is impossible.
    • For this input combination, the given output is not used (perhaps it is ``muxed out'' downstream)

Example (from the book):

• If A or C is true, then D is true (independent of B).
• If A or B is true, then E is true.
• F is true if exactly one of the inputs is true, but we don't care about the value of F if both D and E are true

Full truth table

     A   B   C || D   E   F
     ----------++----------
     0   0   0 || 0   0   0
     0   0   1 || 1   0   1
     0   1   0 || 0   1   1
     0   1   1 || 1   1   0
     1   0   0 || 1   1   1
     1   0   1 || 1   1   0
     1   1   0 || 1   1   0
     1   1   1 || 1   1   1

This has 7 minterms.

Put in the output don't cares

     A   B   C || D   E   F
     ----------++----------
     0   0   0 || 0   0   0
     0   0   1 || 1   0   1
     0   1   0 || 0   1   1
     0   1   1 || 1   1   X
     1   0   0 || 1   1   X
     1   0   1 || 1   1   X
     1   1   0 || 1   1   X
     1   1   1 || 1   1   X

Now do the input don't cares

• B=C=1 ==> D=E=11 ==> F=X ==> A=X
• A=1 ==> D=E=11 ==> F=X ==> B=C=X

     A   B   C || D   E   F
     ----------++----------
     0   0   0 || 0   0   0
     0   0   1 || 1   0   1
     0   1   0 || 0   1   1
     X   1   1 || 1   1   X
     1   X   X || 1   1   X

These don't cares are important for logic minimization. Compare the number of gates needed for the full TT and the reduced TT. There are techniques for minimizing logic, but we will not cover them.

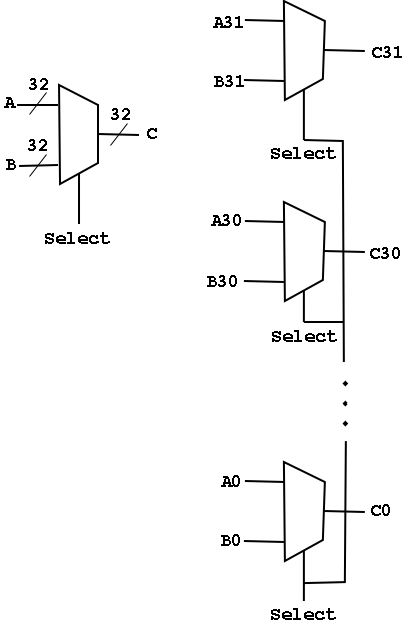
Arrays of Logic Elements

• Do the same thing to many signals
• Draw thicker lines and use the ``by n'' notation.
• Diagram below shows a 32-bit 2-way mux and an implementation with 32 1-bit, 2-way muxes.
• A Bus is a collection of data lines treated as a single logical (n-bit) value.
• Use an array of logic elements to process a bus. For example, the above mux switches between 2 32-bit buses.

Sequential Circuits, Memory, and State

Why do we want to have state?

• Memory (i.e. ram not just rom or prom)
• Counters
• Reducing gate count
  • Multiplier would be quadradic in comb logic.
  • With sequential logic (state) can do in linear.
    • What follows is unofficial (i.e. too fast to understand)
    • Shift register holds partial sum
    • Real slick is to share this shift reg with multiplier
    • We will do this circuit later in the course

Assume you have a real OR gate. Assume the two inputs are both zero for an hour. At time t one input becomes 1. The output will OSCILLATE for a while before settling on exactly 1. We want to be sure we don't look at the answer before its ready.

B.4: Clocks

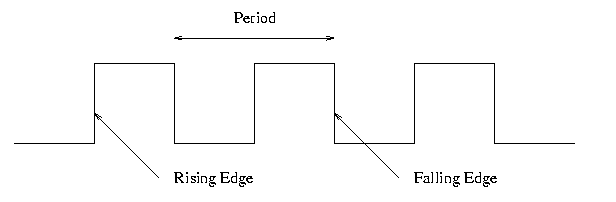
Frequency and period

• Hertz (Hz), Megahertz, Gigahertz vs. Seconds, Microseconds, Nanoseconds
• Old (descriptive) name for Hz is cycles per second (CPS)
• Rate vs. Time

Edges

• Rising Edge; falling edge
• We use edge-triggered logic
• State changes occur only on a clock edge
• Will explain later what this really means
• One edge is called the Active edge
  • The edge (rising or falling) on which changes occur
  • Choice is technology dependent
  • Sometimes trigger on both edges (e.g., RAMBUS or DDR memory)

Synchronous system

Now we are going to add state elements to the combinational circuits we have been using previously.

Remember that a combinational/combinatorial circuits has its outpus determined by its input, i.e. combinatorial circuits do not contain state.

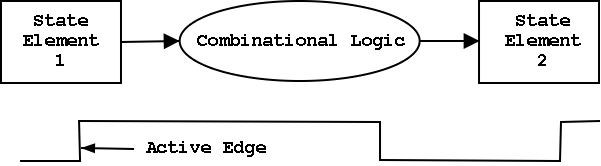
State elements include state (naturally).

• i.e., memory
• state-elements have clock as an input
• can change state only at active edge
• produce output Always; based on current state
• all signals that are written to state elements must be valid at the time of the active edge.
• For example, if cycle time is 10ns make sure combinational circuit used to compute new state values completes in 10ns
• So state elements change on active edge, comb circuit stabilizes between active edges.
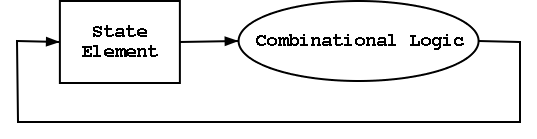
• Think of registers or memory as state elements.
• Can have loops like at the right.
• A loop like this is a cycle of the computer.

B.5: Memory Elements

We want edge-triggered clocked memory and will only use edge-triggered clocked memory in our designs. However we get there by stages. We first show how to build unclocked memory; then using unclocked memory we build level-sensitive clocked memory; finally from level-sensitive clocked memory we build edge-triggered clocked memory.

Unclocked Memory

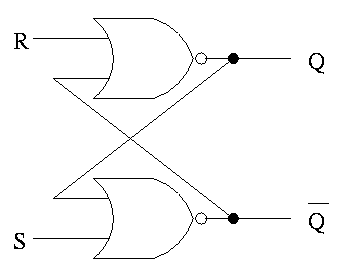
S-R latch (set-reset)

• ``Cross-coupled'' nor gates
• Don't assert both S and R at once
• When S is asserted (i.e., S=1 and R=0)
  • the latch is Set (that's why it is called S)
  • Q becomes true (Q is the output of the latch)
  • Q' becomes false (Q' is the complemented output)
• When R is asserted
  • the latch is Reset
  • Q becomes false
  • Q' becomes true
• When neither one is asserted
  • The latch remains the same, i.e. Q and Q' stay as they were
  • This is the memory aspect

Clocked Memory: Flip-flops and latches

The S-R latch defined above is not clocked memory. Unfortunately the terminology is not perfect.

For both flip-flops and latches the output equals the value stored in the structure. Both have an input and an output (and the complemented output) and a clock input as well. The clock determines when the internal value is set to the current input. For a latch, the change occurs whenever the clock is asserted (level sensitive). For a flip-flop, the change occurs at the active edge.

D latch

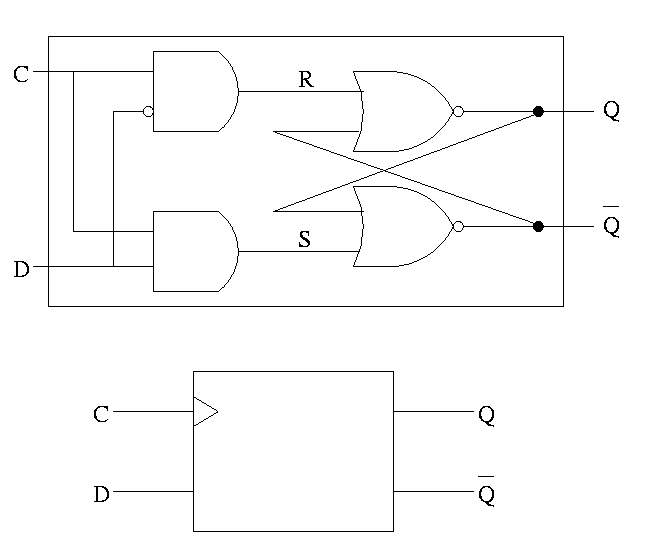
The D is for data

• The left part uses the clock.
  • When the clock is low, both R and S are forced low.
  • When the clock is high, S=D and R=D' so the value store is D.
• Output changes when input changes and the clock is asserted.
• Level sensitive rather than edge triggered.
• Sometimes called a transparent latch.
• We won't use these in designs.
• The right hand part of the circuit is the S-R (unclocked) latch we just constructed.

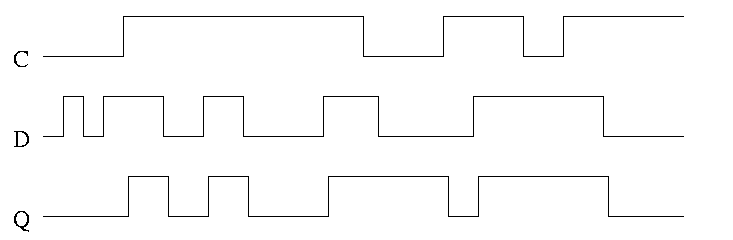
In the traces below notice how the output follows the input when the clock is high and remains constant when the clock is low. We assume the stored value is initially low.

D or Master-Slave Flip-flop

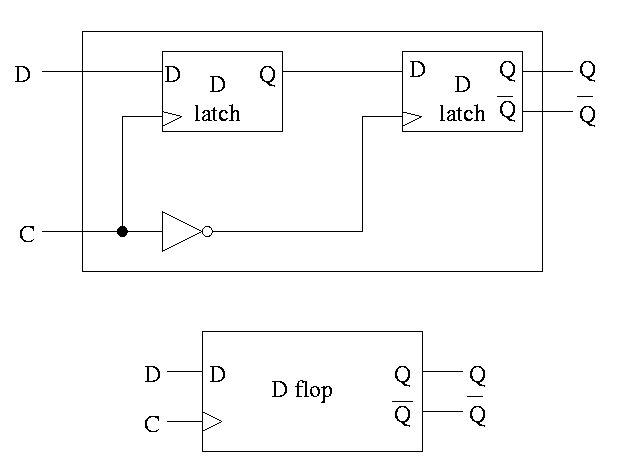
This was our goal. We now have an edge-triggered, clocked memory.

• Built from D latches, which are transparent
• The result is Not transparent
  • Changes on the active edge
  • This one has the falling edge as active edge
• Sometimes called a master-slave flip-flop
• Note substructures with letters reused having different meaning (block structure a la algol)
• Master latch (the left one) is set during the time clock is asserted. Remember that the latch is transparent, i.e. follows its input when its clock is asserted. But the second latch is ignoring its input at this time. When the clock falls, the 2nd latch pays attention and the first latch keeps producing whatever D was at fall-time.
• Actually D must remain constant for some time around the active edge.
  • The set-up time before the edge
  • The hold time after the edge
  • See diagram below

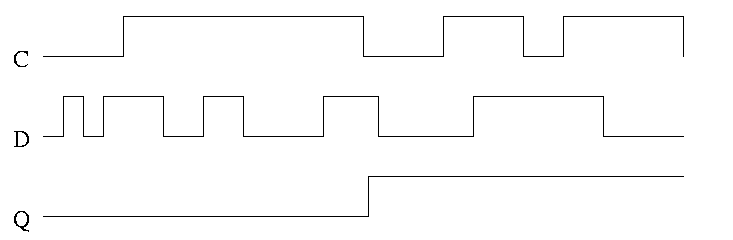
Note how much less wiggly the output is with the master-slave flop than before with the transparent latch. As before we are assuming the output is initially low.

Homework: Try moving the inverter to the other latch What has changed?