================ Start Lecture #11 ================

3.3.2: Page tables

A discussion of page tables is also appropriate for (non-demand) paging, but the issues are more acute with demand paging since the tables can be much larger. Why?
Ans: The total size of the active processes is no longer limited to the size of physical memory.

Want access to the page table to be very fast since it is needed for every memory access.

Unfortunate laws of hardware

Big and fast are essentially incompatible
Big and fast and low cost is hopeless

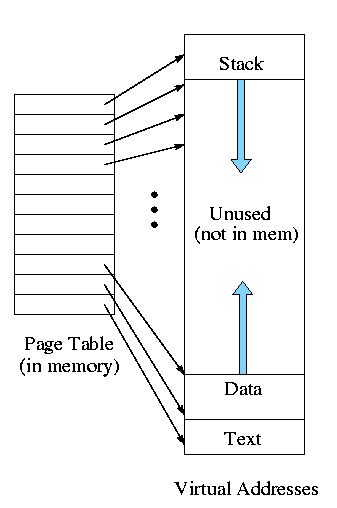
So we can't just say, put the page table in fast processor registers and let it be huge and sell the system for $1500. Put the (one-level) page table in main memory.

Too slow
TLB would help as mentioned above (discussed later in more detail).
Too big
- Currently we are considering contiguous virtual addresses ranges (i.e. the virtual addresses have no holes).
- Typically put the stack at one end of virtual address and the global (or static) data at the other end and let them grow towards each other
- The memory in between is unused.
- This unused memory can be huge (in address range) and hence the page table will mostly contain unneeded PTEs
Works fine if the virtual address range possible is small, which was once true but no longer (e.g. of PDP-11 in Tanenbaum).

Protection bits

Can place protection bits on pages. For example can mark pages as execute only. This requires that boundaries between regions with different protection must be on page boundaries. Protection is more naturally done with segmentation.

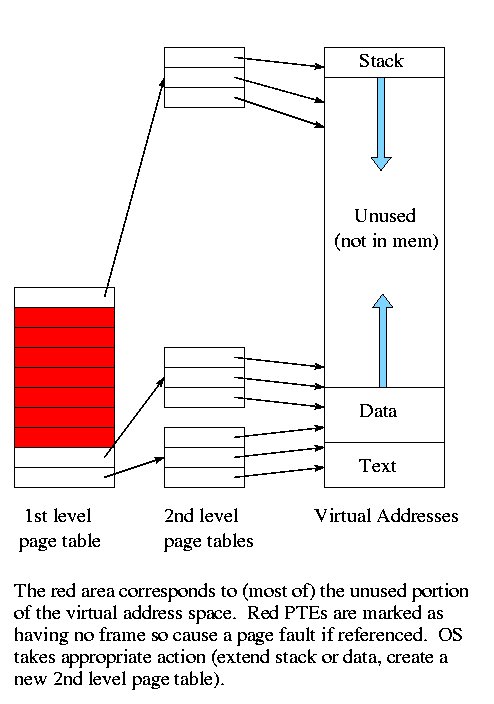
Multilevel page tables

The idea, which is also used in Unix inode-based file systems, is to add a level of indirection and have a page table containing pointers to page tables. This topic will not be on the 202 midterm or final.

Imagine one big page table.
Call it the second level page table and cut it into pieces each the size of a page.
Note that you can get many PTEs in one page so you will have far fewer of these pages than PTEs
Now construct a first level page table containing PTEs that point to these pages.
This first level PT is small enough to store in memory.
But since we still have the 2nd level PT, we have made the world bigger not smaller!
Don't store in memory the 2nd level page tables all of whose PTEs refer to unused memory. That is use demand paging on the (second level) page table

For a two level page table the virtual address is divided into three pieces
```
+-----+-----+-------+
| P#1 | P#2 | Offset|
+-----+-----+-------+
```
P#1 gives the index into the first level page table.
Follow the pointer in the corresponding PTE to reach the frame containing the relevant 2nd level page table.
P#2 gives the index into this 2nd level page table
Follow the pointer in the corresponding PTE to reach the frame containing the (originally) requested frame.
Offset gives the offset in this frame where the requested word is located.

Do an example on the board

The VAX used a 2-level page table structure, but with some wrinkles (see Tanenbaum for details).

Naturally, there is no need to stop at 2 levels. In fact the SPARC has 3 levels and the Motorola 68030 has 4 (and the number of bits of Virtual Address used for P#1, P#2, P#3, and P#4 can be varied).

3.3.4: Associative memory (TLBs)

Note: Tanenbaum suggests that ``associative memory'' and ``translation lookaside buffer'' are synonyms. This is wrong. Associative memory is a general structure and translation lookaside buffer is a special case.

An associative memory is a content addressable memory. That is you access the memory by giving the value of some field and the hardware searches all the records and returns the record whose field contains the requested value.

For example

Name  | Animal | Mood     | Color
======+========+==========+======
Moris | Cat    | Finicky  | Grey
Fido  | Dog    | Friendly | Black
Izzy  | Iguana | Quiet    | Brown
Bud   | Frog   | Smashed  | Green

If the index field is Animal and Iguana is given, the associative memory returns

Izzy  | Iguana | Quiet    | Brown

A Translation Lookaside Buffer or TLB is an associate memory where the index field is the page number. The other fields include the frame number, dirty bit, valid bit, and others.

A TLB is small and expensive but at least it is fast. When the page number is in the TLB, the frame number is returned very quickly.
On a miss, the page number is looked up in the page table. The record found is placed in the TLB and a victim is discarded. There is no placement question since all entries are accessed at the same time. But there is a replacement question.

Homework: 15.

3.3.5: Inverted page tables

Keep a table indexed by frame number with the entry f containg the number of the page currently loaded in frame f.

Since modern machine have a smaller physical address space than virtual address space, the table is smaller
But on a TLB miss, must search the inverted page table.
Would be hopelessly slow except that some tricks are employed.
The book mentions some but not all of the tricks, we are skipping this topic.

3.4: Page Replacement Algorithms

These are solutions to the replacement question.

Good solutions take advantage of locality.

Temporal locality: If a word is referenced now, it is likely to be referenced in the near future.
- This argues for caching referenced words, i.e. keeping the referenced word near the processor for a while
Spatial locality: If a word is referenced now, nearby words are likely to be referenced in the near future.
- This argues for prefetching words around the currently referenced word.
These are lumped together into locality: If a page is referenced, it is likely to be referenced in the near future.
- So it is good to bring in the entire page on a miss and to keep the page in memory for a while.
When programs begin there is no history so nothing to base locality on. At this point the paging system is said to be undergoing a ``cold start''.
Programs exhibit ``phase changes'', when the set of pages referenced changes abruptly (similar to a cold start). At the point of a phase change, many page faults occur because locality is poor.

Pages belonging to processes that have terminated are of course perfect choices for victims.

Pages belonging to processes that have been blocked for a long time are good choices as well.

Random

A lower bound on performance. Any decent scheme should do better.

3.4.1: The optimal page replacement algorithm (opt PRA)

Replace the page whose next reference will be furthest in the future

Also called belady's min algorithm
Provably optimal. That is, generates the fewest number of page faults.
Unimplementable: Requires predicting the future.
Good upper bound on performance

3.4.2: The not recently used (NRU) PRA

Divide the frames into four classes and make a random selection from the lowest nonempty class.

Not referenced, not modified
Not referenced, modified
Referenced, not modified
Referenced, modified

Assumes that in each PTE there are two extra flags R (sometimes called U, for used) and M (often called D, for dirty).

Also assumes that a page in a lower priority class is cheaper to evict

If not referenced, probably not referenced again soon so not so important.
If not modified, do not have to write it out so the cost of the eviction is lower
When a page is brought in, OS resets R and M (i.e. R=M=0)
On a read, hardware sets R
On a write, hardware sets R and M

We again have the prisoner problem, we do a good job of making little ones out of big ones, but not the reverse. Need more resets

Every k clock ticks, reset all R bits

Why not reset M?
Ans: Must have M accurate to know if victim must be written back
Could have two M bits one accurate and one reset, but I don't know of any system (or proposal) that does so.

What if hardware doesn't set these bits?

OS can use tricks
When the bits are reset, make the PTE indicate the page is not resident (i.e. lie). On the page fault, set the appropriate bit(s).

3..4.3: FIFO PRA

Simple but poor since usage of the page is ignored.

Belady's Anomaly: Can have more frames yet more faults. Example given later.

3.4.4: Second chance PRA

Fifo but when time to choose a victim if page at the head of the queue has been referenced (R bit), don't evict it. Instead reset R and move the page to the rear of the queue (so it looks new). The page is being a second chance.

What if all frames have been referenced?
Becomes the same as fifo (but takes longer).

Might want to turn off the R bit more often (k clock ticks).

3.4.5: Clock PRA

Same algorithm as 2nd chance, but a better (and I would say obvious) implementation: Use a circular list.

Do an example.