1. So far the schemes have had two properties
   1. Each job is stored contiguously in memory. That is, the job is contiguous in physical addresses.
   2. Each job cannot use more memory than exists in the system. That is, the virtual addresses space cannot exceed the physical address space.
   
   
2. Tanenbaum now attacks the second item. I wish to do both and start with the first
   
   
3. Tanenbaum (and most of the world) uses the term ``paging'' to mean what I call demand paging. This is unfortunate as it mixes together two concepts
   1. Paging (dicing the address space) to solve the placement problem and essentially eliminate external fragmentation.
   2. Demand fetching, to permit the total memory requirements of all loaded jobs to exceed the size of physical memory.
   
   
4. Tanenbaum (and most of the world) uses the term virtual memory as a synonym for demand paging. Again I consider this unfortunate.
   1. Demand paging is a fine term and is quite descriptive
   2. Virtual memory ``should'' be used in contrast with physical memory to describe any virtual to physical address translation.

** (non-demand) Paging

Simplest scheme to remove the requirement of contiguous physical memory.

• Chop the program into fixed size pieces called pages (invisible to the programmer).
• Chop the real memory into fixed size pieces called page frames or simply frames
• size of a page (the page size) = size of a frame (the frame size)
• Sprinkle the pages into the frames
• Keep a table (called the page table) having an entry for each page. The page table entry or PTE for page p contains the number of the frame f that contains page p.

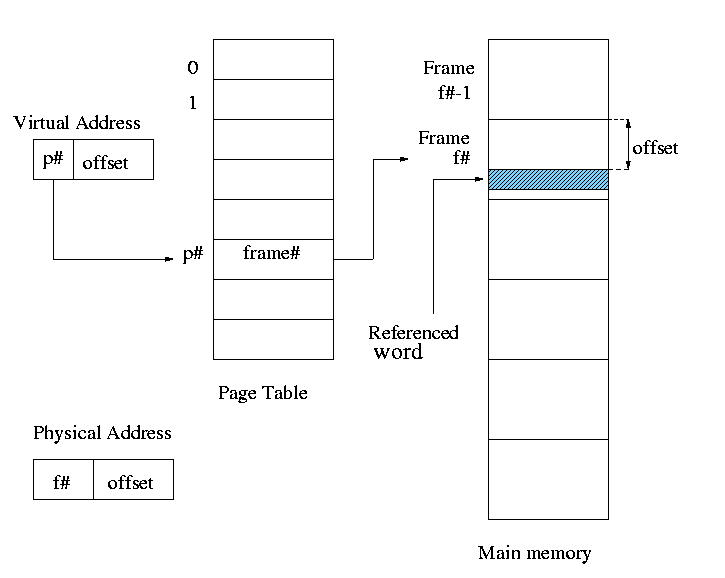
Example: Assume a decimal machine with page size = frame size = 1000.
Assume PTE 3 contains 459.
Then virtual address 3372 corresponds to physical address 459372.

Properties of (non-demand) paging.

• Entire job must be memory resident to run.
• No holes, i.e. no external fragmentation.
• If there are 50 frames available and the page size is 4KB than a job requiring <= 200KB will fit, even if the available frames are scattered over memory.
• Hence (non-demand) paging is useful.
• Introduces internal fragmentation approximately equal to 1/2 the page size for every process (really every segment).
• Can have a job unable to run due to insufficient memory and have some (but not enough) memory available. This is not called external fragmentation since it is not due to memory being fragmented.
• Eliminates the placement question. All pages are equally good since don't have external fragmentation.
• Replacement question unchanged.
• Since page boundaries occur at ``random'' points and can change from run to run (the page size can change with no effect on the program--other than performance), pages are not appropriate units of memory to use for protection and sharing. This is discussed further when we introduce segmentation.

Homework: 13

Address translation

• Each memory reference turns into 2 memory references
  1. Reference the page table
  2. Reference central memory
• This would be a disaster!
• Hence the MMU caches page#-->frame# translations. This cache is kept near the processor and can be accessed rapidly
• This cache is called a translation lookaside buffer (TLB) or translation buffer (TB)
• For the above example, after referencing virtual address 3372, entry 3 in the TLB would contain 459.
• Hence a subsequent access to virtual address 3881 would be translated to physical address 459881 without a memory reference.

Choice of page size is discuss below

Homework: 8, 13, 15.

3.2: Virtual Memory (meaning fetch on demand)

Idea is that a program can execute even if only the active portion of its address space is memory resident. That is, swap in and swap out portions of a program. In a crude sense this can be called ``automatic overlays''.

Advantages

• Can run a program larger than the total physical memory.
• Can increase the multiprogramming level since the total size of the active, i.e. loaded, programs (running + ready + blocked) can exceed the size of the physical memory.
• Since some portions of a program are rarely if ever used, it is an inefficient use of memory to have them loaded all the time. Fetch on demand will not load them if not used and will unload them during replacement if they are not used for a long time (hopefully).

3.2.1: Paging (meaning demand paging)

Fetch pages from disk to memory when they are referenced, with a hope of getting the most actively used pages in memory.

• Very common: dominates modern operating systems
• Started by the Atlas system at Manchester University in the 60s (Fortheringham).
• Each PTE continues to have the frame number if the page is loaded.

  

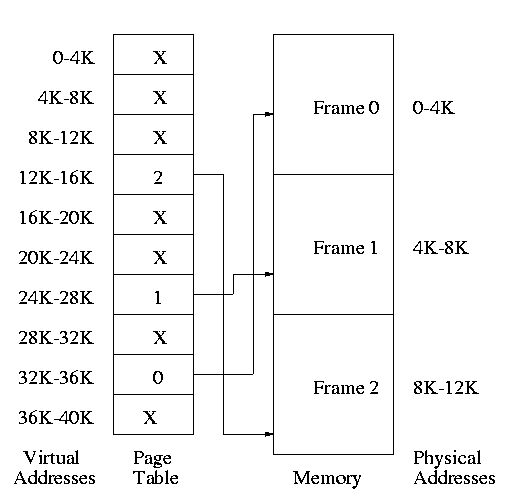
• But what if the page is not loaded (exists only on disk)?
  • The PTE has a flag indicating if loaded (can think of the X in the diagram above as indicating that this flag is not set
  • If not loaded, the location on disk is kept in the PTE (not shown in the diagram)
  • When a reference is made to a non-loaded page (sometimes called a non-existent page, but that is a bad name), the system has a lot of work to do. We give more details below
    1. Choose a free frame if one exists
    2. If not
       1. choose a victim frame
          • More on how to choose later
          • Called the replacement question
       2. write victim back to disk if dirty
       3. update the victim PTE to show not loaded and where on disk it has been put (perhaps the disk location is already there)
    3. Copy the referenced page from disk to the free frame
    4. Update the PTE of the referenced page to show that it is loaded and give the frame number
    5. Do the std paging address translation (p#,off)-->(f#,off)
• Really not done quite this way
  • There is ``always'' a free frame because ...
  • There is a deamon active that checks the number of free frames and if this is too low, chooses victims and ``pages them out'' (writing them back to disk if dirty).
• Size of page table
  • Considerations for plain paging apply
  • Large pages are good for I/O (providing the data is used) since it is faster to do one 16KB I/O than four 4KB I/Os and much faster than sixteen 1KB I/Os

Homework: 11.