You may use C++ for the labs.

The email address for the three e-tutors are

Robert Szarek szar9908@cs.nyu.edu
Aldo J Nunez ajn203@omicron.acf.nyu.edu
Franqueli Mendez fm201@omicron.acf.nyu.edu

Dining Philosophers

A classical problem from Dijkstra

• 5 philosophers sitting at a round table
• Each has a plate of spaghetti
• There is a fork between each two
• Need two forks to eat

• The obvious solution (pick up right; pick up left) deadlocks
• Big lock around everything serializes
• Good code in the book.

The point of mentioning this without giving the solution is to give a feel of what coordination problems are like. The book gives others as well. We are skipping these (again this material would be covered in a sequel course). If you are interested look, for example, at http://allan.ultra.nyu.edu/~gottlieb/courses/1997-98-spring/os/class-notes.html

Homework: 14,15 (these have short answers but are not easy).

Readers and writers

• Two classes of processes
  • Readers, which can work concurrently
  • Writers, which need exclusive access
• Must prevent 2 writers from being concurrent
• Must prevent a reader and a writer from being concurrent
• Must permit readers to be concurrent when no writer is active
• Perhaps want fairness (i.e. freedom from starvation)
• Variants
  1. Writer-priority readers/writers
  2. Reader-priority readers/writers

Quite useful in multiprocessor operating systems. The ``easy way out'' is to treat all processes as writers in which case the problem reduces to mutual exclusion (P and V). The disadvantage of the easy way out is that you give up reader concurrency. Again for more information see the web page referenced above.

2.4: Process Scheduling

Scheduling the processor is often called ``process scheduling'' or simply ``scheduling''.

The objectives of a good scheduling policy include

• Fairness
• Efficiency
• Low response time (important for interactive jobs)
• Low turnaround time (important for batch jobs)
• High throughput [the above are from Tanenbaum]

  ---

• Repeatability. Dartmouth (DTSS) ``wasted cycles'' and limited logins for repeatability.
• Fair across projects
  • ``Cheating'' in unix by using multiple processes
  • TOPS-10
  • Fair share research project
• Degrade gracefully under load

Recall the basic diagram describing process states

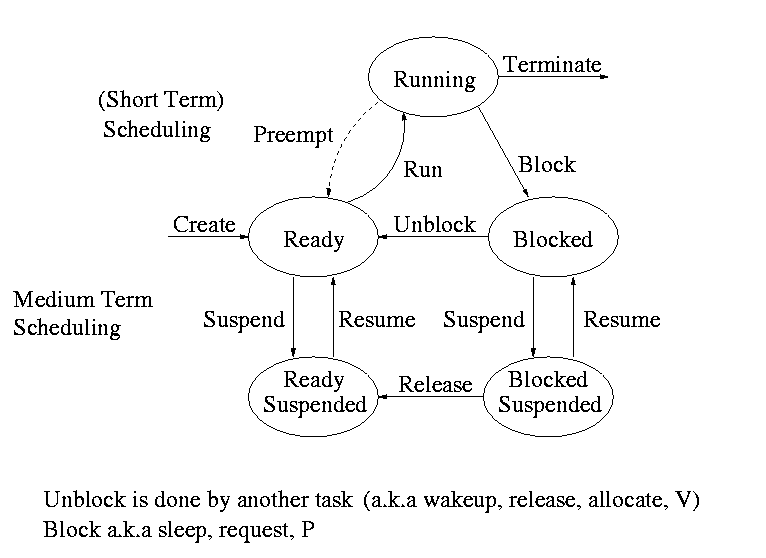
For now we are discussing short-term scheduling running <--> ready.

Medium term scheduling is discussed later.

Preemption

It is important to distinguish preemptive from non-preemptive scheduling algorithms.

• The ``preempt'' arc in the diagram
• Needs a clock interrupt (or equivalent)
• Needed to guarantee fairness
• Found in all modern general purpose operating systems
• Without preemption, the system implements ``run to completion (or yield)''

Deadline scheduling

This is used for real time systems. The objective of the scheduler is to find a schedule for all the tasks (there are a fixed set of tasks) so that each meets its deadline. The run time of each task is known in advance.

Actually it is more complicated.

• Periodic tasks
• What if we can't schedule all task so that each meets its deadline (penalty function)?
• What if the run-time is not constant but has a known probability distribution?

We do not cover deadline scheduling in this course.

The name game

There is an amazing inconsistency in naming the different (short-term) scheduling algorithms. Over the years I have used primarily 4 books: In chronological order they are Finkel, Deitel, Silberschatz, and Tanenbaum. The table just below illustrates the name game for these four books. After the table we discuss each scheduling policy in turn.

Finkel  Deitel  Silbershatz Tanenbaum
-------------------------------------
FCFS    FIFO    FCFS        --    unnamed in tanenbaum
RR      RR      RR          RR      
PS      **      PS          PS
SRR     **      SRR         **    not in tanenbaum
SPN     SJF     SJF         SJF   
PSPN    SRT     PSJF/SRTF   --    unnamed in tanenbaum
HPRN    HRN     **          **    not in tanenbaum
**      **      MLQ         **    only in silbershatz
FB      MLFQ    MLFQ        MQ

First Come First Served (FCFS, FIFO, FCFS, --)

If you ``don't'' schedule, you still have to store the PTEs somewhere. If it is a queue you get FCFS. If it is a stack (strange), you get LCFS. Perhaps you could get some sort of random policy as well.

• Only FCFS is considered
• The simplist scheduling policy
• Non-preemptive

Round Robbin (RR, RR, RR, RR)

• An important preemptive policy
• Essentially the preemptive version of FCFS
• The key parameter is the quantum size q
• When a process is put into the running state a timer is set to q.
• If the timer goes off and the process is still running, the OS preempts the process.
  • This process is moved to the ready state (the preempt arc in the diagram).
  • The next job in the ready list (normally a queue) is selected to run
• As q gets large, RR approaches FCFS
• As q gets small, RR approaches PS (Processor Sharing, described next)
• What value of q should we choose?
  • Tradeoff
  • Small q makes system more responsive
  • Large q makes system more efficient since less switching
• State dependent RR
  • Same as RR but q is varied dynamically depending on the state of the system
  • Favor processes holding important resources
    • For example, non-swappable memory
    • Perhaps medium term scheduling
• External priorities
  • RR but can pay more for bigger q

Homework: 9, 19, 20, 21 (not assigned until lecture 7)

Priority Scheduling

Each job is assigned a priority (externally, perhaps by charging more for higher priority) and the highest priority ready job is run.

• Similar to ``External priorities'' above
• If many processes with the highest priority, use RR among them.
• Can easily starve processes.
• Normally implement priority aging to prevent starvation, that is the priority is raised as the job waits.
• Can have the priorities changed dynamically to favor processes holding important resources (similar to state dependent RR).

Processor Sharing (PS, **, PS, PS)

Merge the ready and running states and permit all ready jobs to be run at once. However, the processor slows down so that when n jobs are running at once each progresses at a speed 1/n as fast if it were running alone.

• Clearly impossible as stated.
• Of theoretical interest (easy to analyze)
• Approximated by RR when the quantum is small. Make sure you understand this point.

Homework: 18.