Producer-consumer problem

• Two classes of processes
  • Producers, which produce times and insert them into a buffer
  • Consumers, which remove items and consume them
• Must worry about the producer encountering a full buffer
• Must worry about the consumer encountering an empty buffer
• Also called the bounded buffer problem.
  • Another example of active entities being replaced by a data structure when viewed at a lower level (Finkel's level principle)

initially e=k, f=0 (counting semaphore); b=open (binary semaphore)

Producer                         Consumer

loop forever                     loop forever
    produce-item                     P(f)
    P(e)                             P(b); take item from buf; V(b)
    P(b); add item to buf; V(b)      V(e)
    V(f)                             consume-item

• k is the size of the buffer
• e represents the number of empty buffer slots
• f represents the number of full buffer slots
• We assume the buffer itself is only serially accessible. That is, only one operation at a time.
  • This explains the P(b) V(b) around buffer operations
  • I use ; and put on one line to suggest that this is simply one operation that is indivisible.
  • Of course this writing style is only a convention, the enforcement of atomicity is done by the P/V
• The P(e), V(f) motif is used to force bounded alternation. If k=1 it gives strict alternation.

Dining Philosophers

A classical problem from Dijkstra

• 5 philosophers sitting at a round table
• each has a plate of spaghetti
• there is a fork between each two
• need two forks to eat

• The obvious soln (pick up right; pick up left) deadlocks
• Big lock around everything serializes
• Good code in the book.

The point of mentioning this without giving the solution is to give a feel of what coordination problems are like. The book gives others as well. We are skipping these (2nd semester, depending on instructor).

Homework: 14,15

Readers and writers

• Two classes of processes
  • Readers, which can work concurrently
  • Writers, which need exclusive access
• Must prevent 2 writers from being concurrent
• Must prevent a reader and a writer from being concurrent
• Must permit readers to be concurrent when no writer is active
• Perhaps want fairness (i.e. freedom from starvation)
• Variants
  1. Writer-priority readers/writers
  2. Reader-priority readers/writers

Quite useful in multiprocessor operating systems. The ``easy way out'' is to treat all as writers (i.e., give up reader concurrency).

2.4: Process Scheduling

Scheduling the processor is often called just scheduling or process scheduling.

The objectives of a good scheduling policy include

• Fairness
• Efficiency
• Low response time (important for interactive jobs)
• Low turnaround time (important for batch jobs)
• High throughput [these are from tanenbaum]

  ---

• Repeatability. Dartmouth (DTSS) ``wasted cycles'' and limited logins for repeatability.
• Fair accross projects
  • ``Cheating'' in unix by using multiple processes
  • TOPS-10
  • Fair share research project
• Degrade gracefully under load

Recall the basic diagram about process states

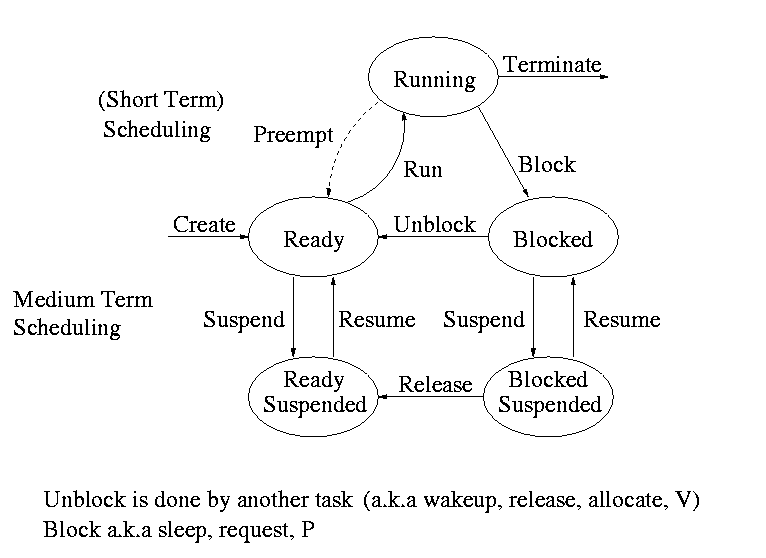
For now we are discussing short-term scheduling running <--> ready.

Medium term scheduling is discussed a little later.

Preemption

This is an important distinction.

• The ``preempt'' arc in the diagram
• Needs a clock interrupt (or equivalent)
• Needed to guarantee fairness
• Found in all modern general purpose operating systems
• Without preemption, the system implements ``run to completion (or yield)''

Deadline scheduling

This is used for real time systems. The objective of the scheduler is to find a schedule for all the tasks (there are a fixed set of tasks) so that each meets its deadline. You know how long each task executes

Actually it is more complicated.

• Periodic tasks
• What if can't schedule all of them (penalty function)?
• What if task time is not constant but has a known probability distribution?

We do not cover deadline schedling in this course.

The name game

There is an amazing inconsistency in naming the different (short-term) scheduling algorithms. Over the years I have used primarily 4 books: In chronological order they are Finkel, Deitel, Silberschatz, and Tanenbaum. The table just below illustrates the name game for these three books. After the table we discuss each scheduling policy in turn.

Finkel  Deitel  Silbershatz Tanenbaum
-------------------------------------
FCFS    FIFO    FCFS        --    unnamed in tanenbaum
RR      RR      RR          RR      
SRR     **      SRR         **    not in tanenbaum
PS      **      PS          PS
SPN     SJF     SJF         SJF   
PSPN    SRT     PSJF/SRTF   --    unnamed in tanenbaum
HPRN    HRN     **          **    not in tanenbaum
**      **      MLQ         **    only in silbershatz
FB      MLFQ    MLFQ        MQ

First Come First Served (FCFS, FIFO, FCFS, --)

If you ``don't'' schedule, you still have to store the PTEs somewhere. If it is a queue you get FCFS. If it is a stack (strange), you get LCFS. Perhaps you could get some sort of random policy as well.

• Only FCFS is considered
• The simplist scheduling policy
• Non-preemptive

Round Robbin (RR, RR, RR, RR)

• An important preemptive policy
• Essentially the preemptive version of FCFS
• The key parameter is the quantum size q
• When a process is put into the running state a timer is set to q.
• If the timer goes off and the process is still running, the OS preempts the process.
  • This process is moved to the ready state (the preempt arc in the diagram.
  • The next job in the ready list (normally a queue) is selected to run
• As q gets large, RR approaches FCFS
• As q gets small, RR approaches PS
• What q should we choose
  • Tradeoff
  • Small q makes system more responsive
  • Large q makes system more efficient since less switching
• State dependent RR
  • Same as RR but q depends on system load
  • Favor processes holding important resourses
    • For example, non-swappable memory
    • Perhaps medium term scheduling
• External priorities
  • RR but can pay more for bigger q

Homework: 9, 19, 20, 21

Selfish RR (SRR, **, SRR, **)

• Perhaps it could be called ``snobbish RR''
• ``Accepted processes'' run RR
• New process waits until its priority reaches that of accepted processes.
• New process starts at prio 0 and increases at rate a>=0
• Accepted process have prio increas at rate b>=0
• Note that at any time all accepted processes have same prio
• If b>a, get FCFS (if b=a, essentially FCFS)
• If b=0, get RR
• If a>b>0, it is interesting

Processor Sharing (PS, **, PS, PS)

All n processes are running, each on a processor 1/n as fast as the real processor.

• Of theoretical interest (easy to analyze)
• Approximated by RR when the quantum is small

Homework: 18.

Shortest Job First (SPN, SJF, SJF)

Sort jobs by total execution time needed and run the shortest first.

• Nonpreemptive
• If we consider the extreme of run-to-completion, i.e. don't even switch on an I/O, then SJF has the shortest average waiting time
  • Moving a short job before a long one decreases the wait for the short by the length of the long and increases the wait of the long by the length of the short.
  • This decreases the total waiting time for these two
  • Hence decreases the total waiting for all and hence decreases the average waiting time as well
• In realistic case where a job has I/O and we switch then, should call the policy shortest next cpu burst first.
• Difficulty is predicting the future (i.e. knowing the time required for job or burst).

Preemptive Shortest Job First (PSPN, SRT, PSJF/SRTF)

Preemptive version of above

• Permit a job that enters the ready list to preempt the running job if the time for the new job (or for its first burst) is less than the remaining time for the running job (or for its current burst).
• Will never happen that an existing job in ready list will require less time than remaining for the current job.
  • Why?
• Can starve jobs that have a long burst.

Priority aging

As a job is waiting, raise its priority and when it is time to choose, pick job with highest priority.

• Can apply this to may policies
• Indeed, many policies can be thought of as priority scheduling in which we run the job with the highest priority (with different notions of priority for different policies).

Homework: 22, 23

Highest Penalty Ratio Next (HPRN, HRN, **, **)