14.4: Client Server

When done on one computer this is the microkernel approach in which the microkernel just supplies interprocess communication and the main OS functions are provided by a number of usermode processes.

This does have advantages. For example an error in the file server cannot corrupt memory in the process server. This makes errors easier to track down.

But it does mean that when a (real) user process makes a system call there are more switches from user to kernel mode and back. These are not free.

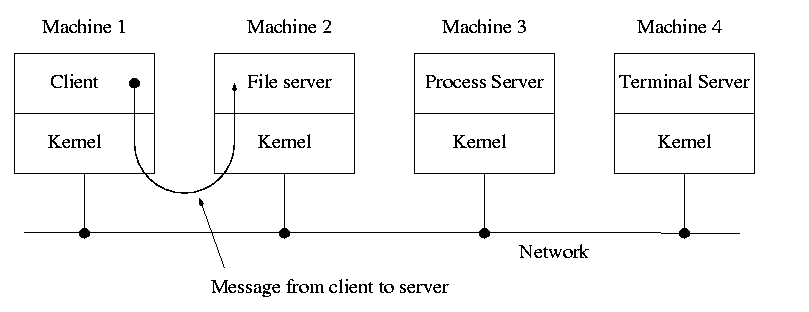
A distributed system can be thought of as an extension of the client server concept where the servers are remote.

Homework: 11

Chapter 2: Process Management

Tanenbaum's chapter title is ``processes''. I prefer process management. The subject matter is process scheduling, interrupt handling, and IPC (Interprocess communication--and coordination).

2.1: Processes

Definition: A process is a program in execution.

Even though in actuality there are many processes running at once, the OS gives each process the illusion that it is running alone.

• We are assuming a multiprogramming OS that automatically switches from one process to another. Sometimes this is called pseudoparallelism since one has the illusion of a parallel processor.
• Virtual time: The time used by just this processes. Progresses at a rate independent of other processes (almost, processes switches get charged a little).
• Virtual memory: The amount of memory the process can ``think it has'' is independent of other processes and each processes believes it is loaded at location zero (say) and has contiguous memory (no holes).

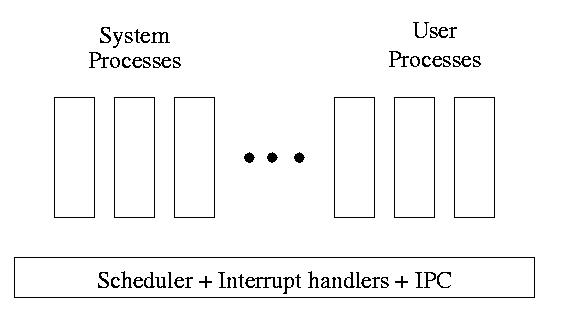
Some systems have user processes and system processes. The latter act as servers satisfying requests from the former (which act as clients). The natural structure of such a system is to have process management (i.e. process switching, interrupt handling, and IPC) in the lowest layer and have the rest of the OS consist of system processes.

This is called the client-server model and is one tanenbaum likes. Indeed, there was reason to believe that it would dominate. But that hasn't happened as yet. One calls such an OS server based. Systems like traditional unix or linux can be called self-service in that the user process itself switches to kernel mode and performs the system call. That is, the same process changes back and forth from/to user<-->system mode and services itself.

Process Hierarchies

Modern general purpose operating systems permit a user to create (and distroy) processes. In unix this is done by the fork system call which creates a child process. Both parent and child keep running (indeed they have the same program text) and each can fork off other processes. A process tree results. The root of the tree is a special process created by the OS during startup.

Process states and transitions

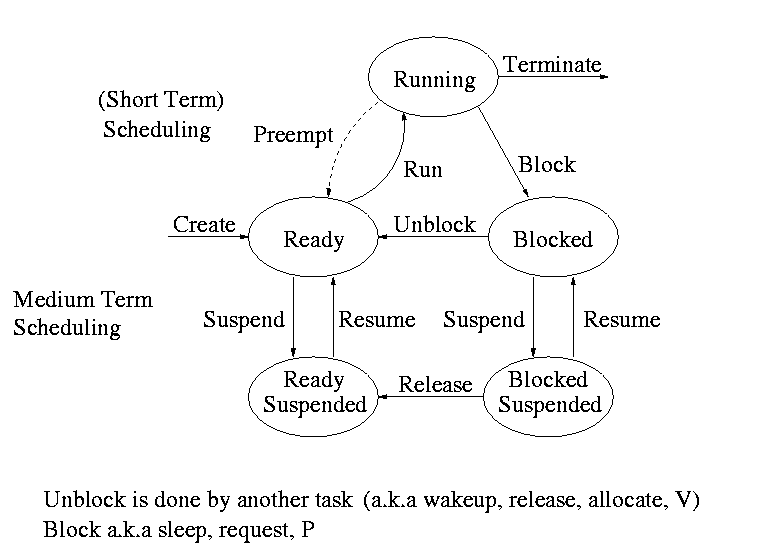
This diagram contains a great deal of information.

• Consider a running process P that issues an I/O request
  • The process blocks
  • At some later point, a disk interrupt occurs and the driver detects that P's request is satisfied.
  • P is unblocked, i.e. is moved from from blocked to ready
  • At some later time the processor looks for a ready job to run and picks P
• A preemptive scheduler has the dotted line preempt;
  A non-preemptive scheduler doesn't
• The number of processes changes only for two arcs: create and terminate
• Suspend and resume are medium term scheduling
  • Done on a larger time scale
  • Involves memory management as well
  • Sometimes called two level scheduling

One can organize an OS around the scheduler.

• Write a minimal ``kernel'' consisting of the scheduler, interrupt handlers, and IPC
• The rest of the OS consists of kernel processes (e.g. memory, filesystem)
• Tanenbaum likes this; his OS ``Minix'' is done this way
• Client server organization

2.1.3: Implementation of Processes

Process table

• One entry per process; often callet PTE (process table entry)
• The central data structure for process management
• A state transition is reflected by a change in the value of a field in the PTE
• We have converted an active entity (process) into a data structure (PTE). Finkel calls this the level principle ``an active entity becomes a data structure when looked at from a lower level''
• The PTE contains a great deal of information about the process
  • Saved value of registers when process not running
  • Stack pointer
  • CPU time used
  • Process id (PID)
  • Process id of parent (PPID)
  • User id (uid and euid)
  • Group id (gid and egid)
  • Pointer to text segment (memory for the program text)
  • Pointer to data segment
  • Pointer to stack segment
  • UMASK (default permissions for new files)
  • Current working directory (cwg)
  • Many others

An aside on interupts

In a well defined location in memory (specified by the hardware) the OS store aninterrupt vector, which contains the address of the (first level) interrupt handler.

• Tanenbaum calls this the interrupt service routine.
• Actually one can have different priorities of interrupts and the interrupt contains one pointer for each level. This is why it is called a vector

Assume a process P is running and an interrupt occurs (say a disk interrupt for the completion of a disk read previously issued by process Q). Note that the interrupt is unlikely to be for process P.

1. The hardware stacks the program counter etc (possibly some registers)
2. Hardware loads new program counter from the interrupt vector.
   • Loading program counter causes a jump
   • Steps 1 and 2 are similar to a procedure call. But the interrupt is asynchronous
3. Assembly language routine saves registers
4. Assembly routine sets up new stack
   • These last two steps can be called setting up the C environment
5. Assembly routine calls C procedure (tanenbaum forgot this one)
6. C procedure does the real work
   • Determines what caused the interrupt (in this case a disk completed an I/O)
     • How does it figure out the cause?
     • Which priority interrupt was activated.
     • The controller can write data in memory before the interrupt
     • The OS can read registers in the controller
   • Mark process Q. The code to run may well be OS code (e.g. the OS may need to copy the data just read from a buffer into the user's space).
   • Now we have at least two processes to run: P and Q
   • The scheduler decides which process to run (P or Q or something else). Lets assume that the decision is to run P.
7. The C procedure (that did the real work in the interrupt processing) continues and returns to the assembly code.
8. Assembly language starts P at the point it was when the interrupt occurred.

2.2: Interprocess Communication (IPC)

2.2.1: Race Conditions

A race condition occurs when two processes can interact and the outcome depends on the order in which the processes execute.

• Imagine two processes both accessing x, which is initially 10.
  • One process is to execute x <-- x+1
  • The other is to execute x <-- x-1
  • When both are finished x should be 10
  • But we might get 9 and might get 11!
  • Show how this can happen (x <-- x+1 is not atomic)
  • Tanenbaum shows how this can lead to disaster for a printer spooler

2.2.2: Critical sections

Prevent interleaving of sections of code that need to be atomic with respect to each other. That is, the conflicting sections need mutual exclusion. If process A is executing its critical section, it excludes process B from executing its critical section. Conversely if process B is executing is critical section, it excludes process A from executing its critical section.

Goals for a critical section implementation.

1. No two processes may be simultaneously inside their critical section
2. No assumption may be made about the speeds or the number of CPUs
3. No process outside its critical section may block other processes
4. No process should have to wait forever to enter its critical section
   • I do NOTE make this last requirement.
   • I just require that the system as a whole make progress (so not all processes are blocked)
   • I refer to solutions that do not satisfy tanenbaum's last condition as unfair (but nonetheless correct) solutions

2.2.3 Mutual exclusion with busy waiting

The operating system can choose not to preempt itself. That is, no preemption for system processes (if the OS is client server) or for processes running in system mode (if the OS is self service)

But this is not adequate

• Does work for user programs
• Doesn't prevent conflicts between the main line OS and interrupt handlers
  • This could be prevented by blocking interrupts while the mail line is in its critical section.
  • Indeed, this is done.
  • Don't want to block interrupts for too long or system seems unresponsivie
• Doesn't work if you have several processors
  • Both main lines can conflict
  • One processor cannot block interrupts on the other

Software solutions for two processes

Initially P1wants=P2wants=false

Code for P1                             Code for P2

Loop forever {                          Loop forever {
    P1wants <-- true         ENTRY          P2wants <-- true
    while (P2wants) {}       ENTRY          while (P1wants) {}
    critical-section                        critical-section
    P1wants <-- false        EXIT           P2wants <-- false
    non-critical-section }                  non-critical-section }

Explain why this works.

But it is wrong! Why?

Initially turn=1

Code for P1                      Code for P2

Loop forever {                   Loop forever {
    while (turn = 2) {}              while (turn = 1) {}
    critical-section                 critical-section
    turn <-- 2                       turn <-- 1
    non-critical-section }           non-critical-section }

This one forces alternation, so is not general enough.

In fact, it took years (way back when) to find a correct solution. The first one was found by dekker. It is very clever, but I am skipping it (I cover it when I teach OS II).

Initially P1wants=P2wants=false  and  turn=1

Code for P1                        Code for P2

Loop forever {                     Loop forever {
    P1wants <-- true                   P2wants <-- true
    turn <-- 2                         turn <-- 1
    while (P2wants and turn=2) {}      while (P1wants and turn=1) {}
    critical-section                   critical-section
    P1wants <-- false                  P2wants <-- false
    non-critical-section               non-critical-section

This is Peterson's solution. When it was published, it was a surprise to see such a simple soluntion. In fact Peterson gave a solution for any number of processes. Subsequently, algorithms with better fairness properties were found (e.g. no task has to wait for another task to enter the CS twice). We will not cover these.

Hardware assist (test and set)

Now implementing a critical section for any number of processes is trivial.

while (TAS(s)) {}   ENTRY
s<--false           EXIT

P and V and Semaphores

Note: Tanenbaum does both busy waiting (like above) and blocking (process switching) solutions. We will only do busy waiting.

Homework: 3

The entry code is often called P and the exit code V (tanenbaum only uses P and V for blocking, but we use it for busy waiting). So the critical section problem is to write P and V so that

loop forever
    P
    critical-section
    V
    non-critical-section

1. Mutual exclusion
2. Forward progress (my weaken version of tanenbaum's condition
3. No speed assumptions
4. No blocking by processes in NCS

Note that I use indenting carefully and hence do not need (and sometimes omit) the braces {}

A binary semaphore abstracts the TAS solution we gave for the critical section problem.

• A binary semaphore S takes on two possible values ``open'' and ``closed''
• Two operations are supported
• P(S) is

      while (S=closed)
      S<--closed     <== This is NOT the body of the while
  

  where finding S=open and setting S<--closed is atomic
• That is, wait until the gate is open, then run through and atomically close the gate
• Said another way, it is not possible for two processes doing P(S) simultaneously to both see S=open (unless a V(S) intervenes).
• V(S) is simply S<--open

So for any number of processes the critical section problem can be solved by

loop forever
    P(S)
    CS     <== critical-section
    V(S)
    NCS    <== non-critical-section

The only solution we have seen for arbitrary number of processes is with test and set.

To solve other coordination problems we want to extend binary semaphores

• With binary semaphores, two consecutive Vs do not permit two subsequent Ps to succeed (the gate cannot be doubly opened).
• We might want to limit the number of processes in the section to 3 or 4, not always just 1.
  

The solution to both of these shortcomings is to remove the restriction to a binary variable and define a generalized or counting semaphore.

• A counting semaphore S takes on non-negative integer values
• Two operations are supported
• P(S) is

      while (S=0)
      S--
  

  where finding S>0 and decrementing S is atomic
• That is, wait until the gate is open (positive), then run through and atomically close the gate one unit
• Said another way, it is not possible for two processes doing P(S) simultaneously to both see the same positive value of S unless a V(S) intervenes.
• V(S) is simply S++

These counting semaphores can solve what I call the semi-critical-section problem, where you premit up to k processes in the section. When k=1 we have the original critical-section problem.

initially S=k

loop forever
    P(S)
    SCS   <== semi-critical-section
    V(S)
    NCS