======== START LECTURE #24
========
Homework: 7.39, 7.40 (should have been asked earlier)
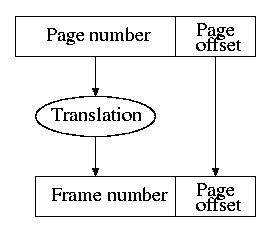
- For both caching and demand paging, the placement
question is trivial since the items are fixed size (no first-fit,
best-fit, buddy, etc).
- The replacement question is not trivial. (H&P
list this under the placement question, which I believe is in error).
Approximations to LRU are popular for both caching and demand
paging.
- The cost of a page fault vastly exceeds the cost of a cache miss
so it is worth while in paging to slow down hit processing to lower
the miss rate. Hence demand paging is fully associative and uses a
table to locate the frame in which the page is located.
- The figures to the right are for demand paging. But they can be
interpreted for caching as well.
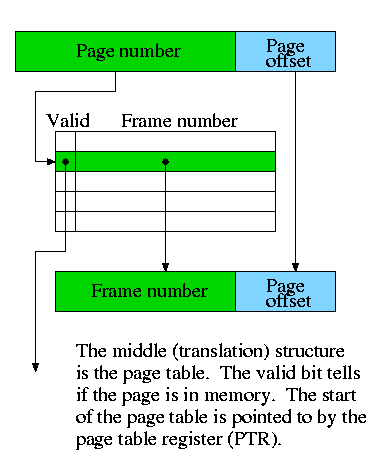
- The (virtual) page number is the memory block number
- The Page offset is the word-in-block
- The frame (physical page) number is the cache block number
(which is the index into the cache).
- Since demand paging uses full associativity, the tag is the
entire memory block number. Instead of checking every cache block
to see if the tags match, a (page) table is used.
- There are of courses differences as well.
- When the valid bit is off for a cache entry, the entry is
junk.
- When the valid bit is off for a page table entry, then entry
still contains important data, specifically the location on the
disk where the page can be found.
Homework: 7.32
Write through vs. write back
Question: On a write hit should we write the new value through to
(memory/disk) or just keep it in the (cache/memory) and write it back
to (memory/disk) when the (cache-line/page) is replaced.
- Write through is simpler since write back requires two operations
at a single event.
- But write-back has fewer writes to (memory/disk) since multiple
writes to the (cache-line/page) may occur before the (cache-line/page)
is evicted.
- For caching the cost of writing through to memory is probably less
than 100 cycles so with a write buffer the cost of write through is
bearable and it does simplify the situation.
- For paging the cost of writing through to disk is on the order of
1,000,000 cycles. Since write-back has fewer writes to disk, it is used.
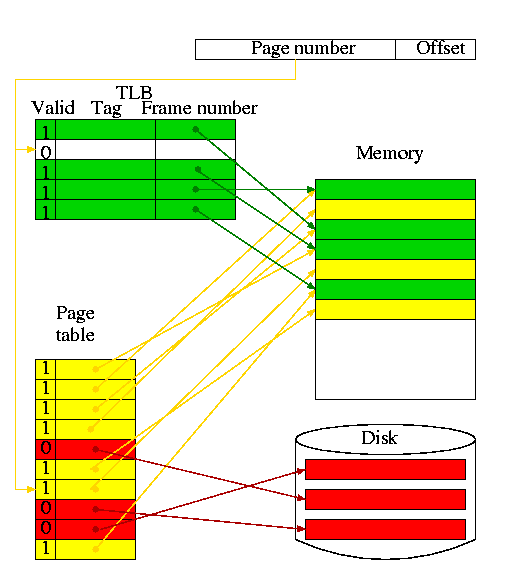
Translation Lookaside Buffer (TLB)
A TLB is a cache of the page table
- Needed because otherwise every memory reference in the program
would require two memory references, one to read the page table and
one to read the requested memory word.
- Typical TLB parameter values
- Size: hundreds of entries
- Block size: 1 entry
- Hit time: 1 cycle
- Miss time: tens of cycles
- Miss rate: Low (<= 2%)
- In the diagram on the right
- The green path is the fastest (TLB hit)
- The red is the slowest (page fault)
- The yellow is in the middle (TLB miss, no page fault)
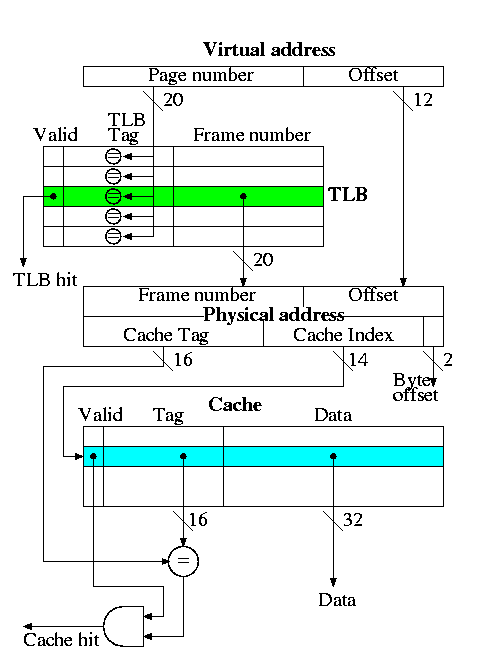
Putting it together: TLB + Cache
This is the decstation 3100
- Virtual address = 32 bits
- Physical address = 32 bits
- Fully associative TLB (naturally)
- Direct mapped cache
- Cache blocksize = one word
- Pagesize = 4KB = 2^12 bytes
- Cache size = 16K entries = 64KB
Actions taken
- The page number is searched in the fully associative TLB
- If a TLB hit occurs, the frame number from the TLB together with
the page offset gives the physical address. A TLB miss causes an
exception to reload the TLB, which we do not discuss.
- The physical address is broken into a cache tag and cache index
(plus a two bit byte offset that is not used for word references).
- If the reference is a write, just do it without checking for a
cache hit (this is possible because the cache is so simple as we
discussed previously).
- For a read, if the tag located in the cache entry specified by the
index matches the tag in the physical address, the referenced word has
been found in the cache; i.e., we had a read hit.
- For a read miss, the cache entry specified by the index is fetched
from memory and the data returned to satisfy the request.
Hit/Miss possibilities
| TLB | Page | Cache | Remarks |
|---|
| hit | hit | hit |
Possible, but page table not checked on TLB hit, data from cache |
| hit | hit | miss |
Possible, but page table not checked, cache entry loaded from memory |
| hit | miss | hit |
Impossible, TLB references in-memory pages |
| hit | miss | miss |
Impossible, TLB references in-memory pages |
| miss | hit | hit |
Possible, TLB entry loaded from page table, data from cache |
| miss | hit | miss |
Possible, TLB entry loaded from page table, cache entry loaded from memory |
| miss | miss | hit |
Impossible, cache is a subset of memory |
| miss | miss | miss |
Possible, page fault brings in page, TLB entry loaded, cache loaded |
Homework: 7.31, 7.33
7.5: A Common Framework for Memory Hierarchies
Question 1: Where can the block be placed?
This could be called the placement question. There is
another placement question in OS memory memory management. When
dealing with varying size pieces (segmentation or whole program
swapping), the available space becomes broken into varying size
available blocks and varying size allocated blocks (called holes). We
do not discussing the above placement question in this course (but
presumably it was in 204 when you took it and for sure it will be in
204 next semester--when I teach it).
The placement question we do study is the associativity of the
structure.
Assume a cache with N blocks
- For a direct mapped caches a block can only be placed in one
slot. That is, there is one block per set and hence the number of
sets equals N, the number of blocks.
- For fully associative caches the block can be placed in any of the
N slos. That is, there are N blocks per set and hence one set.
- For k-way associative caches the block can be placed in any of k
slots. That is, there are k blocks per set and hence N/k sets
- 1-way assosciativity is direct mapped.
- For a cache with n blocks, n-way associativity is the same as
fully associative.
Typical Values
| Feature |
Typical values
for caches |
Typical values
for paged memory |
Typical values
for TLBs |
| Size |
8KB-8MB |
16MB-2GB |
256B-32KB |
| Block size |
16B-256B |
4KB-64KB |
4B-32B |
| Miss penalty in clocks |
10-100 |
1M-10M |
10-100 |
| Miss rate |
.1%-10% |
.000001-.0001% |
.01%-2% |
|
Question 2: How is a block found?
| Associativity | Location method | Comparisons Required |
|---|
| Direct mapped | Index | 1 |
| Set Associative | Index the set, search among elements
| Degree of associativity |
| Full | Search all cache entries
| Number of cache blocks |
| Separate lookup table | 0 |
The difference in sizes and costs for demand paging vs. caching,
leads to a different choice implementation of finding the block.
Demand paging always uses the bottom row with a separate table (page
table) but caching never uses such a table.
- With page faults so expensive, misses must be reduced as much as
possible. Hence full associativity is used.
- With page faults so expensive, a software implementation can be
used so no extra hardware is needed to index the table.
- The large block size (called page size) means that the extra table
is a small fraction of the space.
Question 3: Which block should be replaced?
This is called the replacement question and is much
studied in demand paging (remember back to 202).
- For demand paging with miss costs so high and associativity so
high (fully associative), the replacement policy is important and some
approximation to LRU is used.
- For paging, the hit time must be small so simple schemes are
used. For 2-way associativity, LRU is trivial. For higher
associativity (but associativity is never very high) crude
approximations may be used and sometimes random.
replacement is used.
Question 4: What happens on a write?
- Write-through
- Data written to both the cache and main memory (in general to
both levels of the hierarchy).
- Sometimes used for caching, never used for demand paging
- Advantages
- Misses are simpler and cheaper (no copy back)
- Easier to implement, especially for block size 1, which we
did in class.
- For blocksize > 1, a write miss is more complicated since
the rest of the block now is invalid. Fetch the rest of the
block from memory (or mark those parts invalid by extra valid
bits--not covered in this course).
Homework: 7.41
- Write-back
- Data only written to the cache. The memory has stale data,
but becomes up to date when the cache block is subsequently
replaced in the cache.
- Only real choice for demand paging since writing to the lower
level of the memory hierarch (in this case disk) is so slow.
- Advantages
- Words can be written at cache speed not memory speed
- When blocksize > 1, writes to multiple words in the cache
block are only written once to memory (when the block is
replaced).
- Multiple writes to the same word in a short period are
written to memory only once.
- When blocksize > 1, the replacement can utilize a high
bandwidth transfer. That is, writing one 64-byte block is
faster than 16 writes of 4-bytes each.



