• Why is set associativity bad?
  It is a little slower due to the mux and AND gate.
• Which block (in the set) should be replaced?
  • Random is sometimes used
    
  • LRU is better but not so easy to do quickly.
    • If the cache is 2-way set associative, each set is of size two and it is easy to find the lru block quickly. How?
      For each set keep a bit indicating which block in the set was just referenced and the lru block is the other one.
    • If the cache is 4-way set associative, each set is of size 4. Consider these 4 blocks as two groups of 2. Use the trick above to find the group most recently used and pick the other group. Also use the trick within each group and chose the block in the group not used last.
    • Sound great. We can do lru fast. Wrong! The above is not LRU it is just an approximation. Show this on the board.

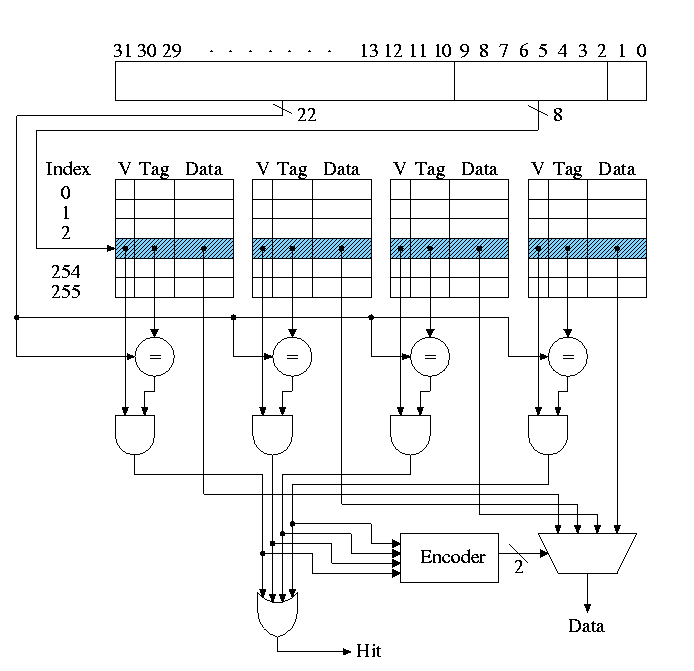
Tag size and division of the address bits

We continue to assume a byte addressed machines, but all references are to a 4-byte word (lw and sw).

The 2 LOBs are not used (they specify the byte within the word but all our references are for a complete word). We show these two bits in dark blue. We continue to assume 32 bit addresses so there are 2**30 words in the address space.

Let's review various possible cache organizations and determine for each how large is the tag and how the various address bits are used. We will always use a 16KB cache. That is the size of the data portion of the cache is 16KB = 4 kilowords = 2**12 words.

1. Direct mapped, blocksize 1 (word).
   • Since the blocksize is one word, there are 2**30 memory blocks and all the address bits (except the 2 LOBs that specify the byte within the word) are used for the memory block number. Specifically 30 bits are so used.
   • The cache has 2**12 words, which is 2**12 blocks.
   • So the low order 12 bits of the memory block number give the index in the cache (the cache block number), shown in cyan.
   • The remaining 18 (30-12) bits are the tag, shown in red.
   
   
   
2. Direct mapped, blocksize 8
   • Three bits of the address give the word within the 8-word block. These are drawn in magenta.
   • The remaining 27 HOBs of the memory address give the memory block number.
   • The cache has 2**12 words, which is 2**9 blocks.
   • So the low order 9 bits of the memory block number gives the index in the cache.
   • The remaining 18 bits are the tag
   
   
3. 4-way set associative, blocksize 1
   • Blocksize is 1 so there are 2**30 memory blocks and 30 bits are used for the memory block number.
   • The cache has 2**12 blocks, which is 2**10 sets (each set has 4=2**2 blocks).
   • So the low order 10 bits of the memory block number gives the index in the cache.
   • The remaining 20 bits are the tag. As the associativity grows the tag gets bigger. Why?
     Growing associativity reduces the number of sets into which a block can be placed. This increases the number of memory blocks that be placed in a given set. Hence more bits are needed to see if the desired block is there.
   
   
4. 4-way set associative, blocksize 8
   • Three bits of the address give the word within the block.
   • The remaining 27 HOBs of the memory address give the memory block number.
   • The cache has 2**12 words = 2**9 blocks = 2**7 sets.
   • So the low order 7 bits of the memory block number gives the index in the cache.

Improvement: Multilevel caches

Modern high end PCs and workstations all have at least two levels of caches: A very fast, and hence not too big, first level (L1) cache together with a larger but slower L2 cache.

When a miss occurs in L1, L2 is examined and only if a miss occurs there is main memory referenced.

So the average miss penalty for an L1 miss is

(L2 hit rate)*(L2 time) + (L2 miss rate)*(L2 time + memory time)

Do an example

• Assume
  1. L1 I-cache miss rate 4%
  2. L2 D-cache miss rate 5%
  3. 40% of instructions reference data
  4. L2 miss rate 6%
  5. L2 time of 15ns
  6. Memory access time 100ns
  7. Base CPI of 2
  8. Clock rate 400MHz
• How many instructions per second does this machine execute
• How many instructions per second would this machine execute if the L2 cache were eliminated.
• How many instructions per second would this machine execute if both caches were eliminated.
• How many instructions per second would this machine execute if the L2 cache had a 0% miss rate (L1 as originally specified).
• How many instructions per second would this machine execute if both L1 caches had a 0% miss rate

7.4: Virtual Memory

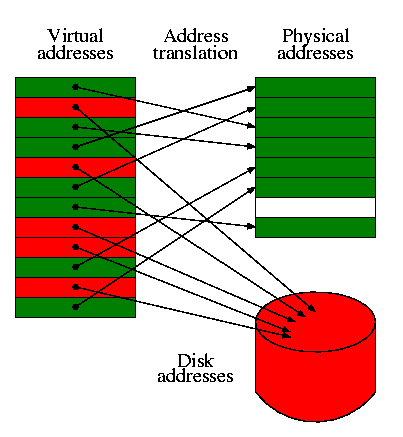
I realize this material was covered in operating systems class (V22.0202). I am just reviewing it here. The goal is to show the similarity to caching, which we just studied. Indeed, (the demand part of) demand paging is caching: In demand paging the memory serves as a cache for the disk, just as in caching the cache serves as a cache for the memory.

The names used are different and there are other differences as well.

Cache concept	Demand paging analogue
Memory block	Page
Cache block	Page Frame (frame)
Blocksize	Pagesize
Tag	None (table lookup)
Word in block	Page offset
Valid bit	Valid bit

Cache concept	Demand paging analogue
Associativity	None (fully associative)
Miss	Page fault
Hit	Not a page fault
Miss rate	Page fault rate
Hit rate	1 - Page fault rate
Placement question	Placement question
Replacement question	Replacement question

• For both caching and demand paging, the placement question is trivial since the items are fixed size (no first-fit, best-fit, buddy, etc).
• The replacement question is not trivial. (H&P list this under the placement question, which I believe is in error). Approximations to LRU are popular for both caching and demand paging.
• The cost of a page fault vastly exceeds the cost of a cache miss so it is worth while in paging to slow down hit processing to lower the miss rate. Hence demand paging is fully associative and uses a table to locate the frame in which the page is located.
• Hand out figures 7.21 and 7.22 from H&P and show how to interpret them for caching.
  • The (virtual) page number is the memory block number
  • The Page offset is the word-in-block
  • The frame (physical page) number is the cache block number (which is the index into the cache).
  • Since demand paging uses full associativity, the tag is the entire memory block number. Instead of checking every cache block to see if the tags match, a (page) table is used.