Homework: 7.2 7.3 (should have been give above with 7.1. I changed the notes so this is fix for ``next time'')

Improvement: Use a write buffer

• Hold a few (four is common) writes at the processor while they are being processed at memory.
• As soon as the word is written into the write buffer, the instruction is considered complete and the next instruction can begin.
• Hence the write penalty is eliminated as long as the word can be written into the write buffer.
• Must stall (i.e., incur a write penalty) if the write buffer is full. This occurs if a bunch of writes occur in a short period.
• If the rate of writes is greater than the rate at which memory can handle writes, you must stall eventually. The purpose of a write-buffer (indeed of buffers in general) is to handle short bursts.
• The Decstation 3100 had a 4-word write buffer.

Unified vs split I and D (instruction and data)

• Given a fixed total size of caches, is it better to have two caches, one for instructions and one for data; or is it better to have a single ``unified'' cache?
• Unified is better because better ``load balancing''. If the current program needs more data references than instruction references, the cache will accomodate. Similarly if more instruction references are needed.
• Split is better because it can do two references at once (one instruction reference and one data reference).
• The winner is ...
  split I and D.
• But unified has the better (i.e. higher) hit ratio.
• So hit ratio is not the ultimate measure of good cache performance.

Improvement: Blocksize > Wordsize

• The current setup does not take any advantage of spacial locality. The idea of larger blocksizes is to bring in words near the referenced word since, by spacial locality, they are likely to be referenced in the near future.
• The figure below shows a direct mapped cache with 4-word blocks.

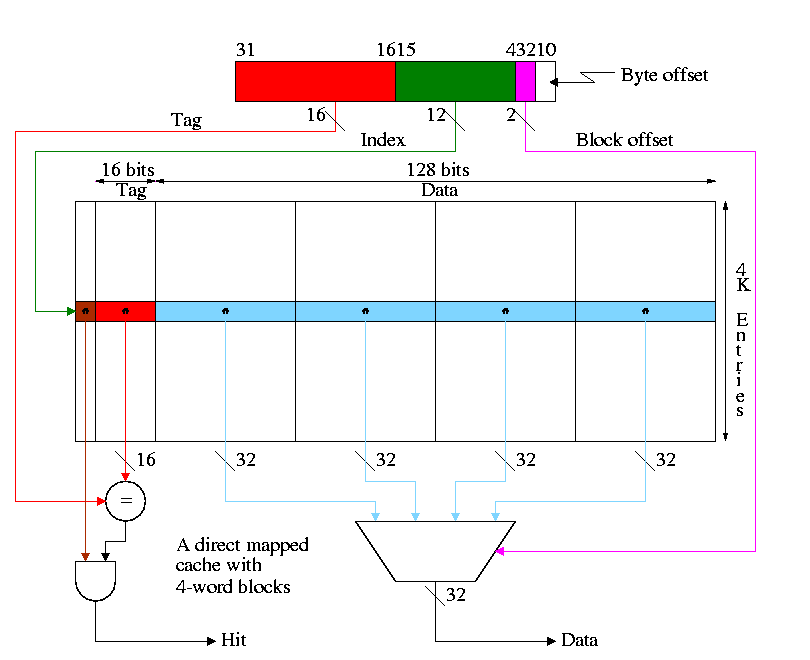
• What addresses in memory are in the block and where in the cache do they go?
  • The memory block number =
    the word address / number of words per block =
    the byte address / number of bytes per block
  • The cache block number =
    the memory block number modulo the number of blocks in the cache
  • The block offset =
    the word address modulo the number of words per block
  • The tag =
    the word addres / the number of words in the cache =
    the byte address / the number of bytes in the cache
  • Show from the diagram how this gives the red portion for the tag and the green portion for the index or cache block number.
• Consider the cache shown in the diagram above and a reference to word 17001.
  • 17001 / 4 gives 4250 with a remainder of 1
  • So the memory block number is 4250 and the block offset is 1
  • 4K=4096 and 4250 / 4096 gives 0 with a remainder of 154.
  • So the cache block number is 154.
  • Putting this together a reference to word 17001 is a reference to the first word of the cache block with index 154
  • The tag is 17001 / (4K * 4) = 1
• Cachesize = Blocksize * #Entries. For the diagram above this is 64KB.
• Calculate the total number of bits in this cache and in one with one word blocks but still 64KB of data
• If the references are strictly sequential the pictured cache has 75% hits; the simplier cache with one word blocks has no hits.

Homework: 7.7 7.8 7.9

Why not make blocksize enormous? Cache one huge block.

• NOT all access are sequential
• With too few blocks misses go up again

Memory support for wider blocks

• Should memory be wide?
• Should the bus be wide?

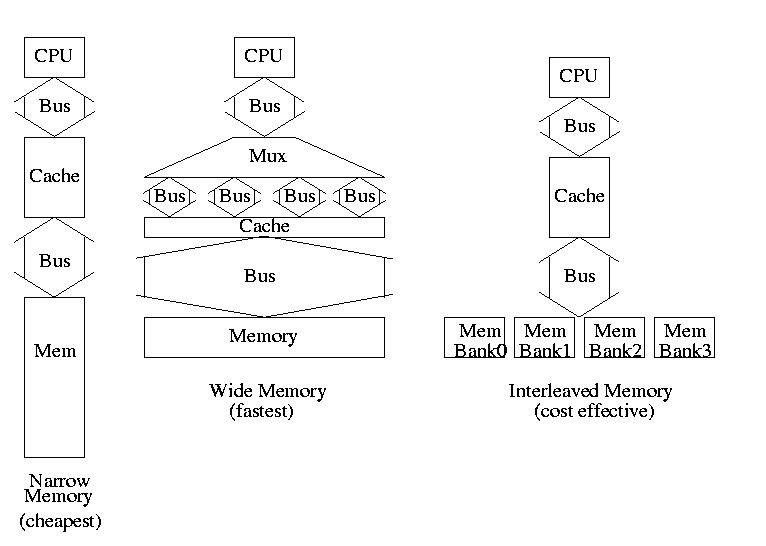
• Assume
  1. 1 clock to send the address only one address for all designs
  2. 15 clocks for each memory access (independent of width)
  3. 1 Clock/busload of data
• Narrow design (a) takes 65 clocks for a read miss since must make 4 memory requests (do it on the board)
• Wide design (b) takes 17
• Interleaved (c) takes 20
• Interleaving works great because in this case we are guaranteed to have sequential accesses
• Imagine design between (a) and (b) with 2-word wide datapath Takes 33 cycles and more expensive to build than (c)

Homework: 7.11